为什么会错了
张燕敏

一、缘起:聚焦细节,为什么会错了
“人民币的简单计算”是新人教版一年级数学下册第5单元第46-55页的内容。其主要是让学生在认识人民币的基础上学习使用人民币,在买东西的过程中进行简单计算。现行教材尊重并充分利用学生已有生活经验,在认币、换币和取钱、付钱、找钱等活动中掌握人民币的知识和简单的购物技能。学生在生活中都见过人民币,或多或少有一些认识,部分学生还有购物的经验。在这一出发点下,笔者听到的“人民币的简单计算”这一课大多是 “去超市选购东西”为情景导入教学,然后通过“售货员”“顾客”这两个角色的对话进行新课知识的学习。其中有个细小的对话片段引起了笔者的思考,特摘录下来,供大家一起探讨研究:
案例1:
师:假如你有10元钱,你想买什么?(然后出现课本例8的购物图片)
生1:我想买一个皮球,10元-6元=4元,我还可以找回4元。
生2:我想买一个乒乓板,10元-8元=2元,我还可以找回2元。
(这两个东西买好后,教室里就保持沉默,举手的同学寥寥无几。)
教师有点奇怪,追问道:还有想买的吗?
生3:老师,我想买小熊可以吗?
师:可以。
生4(举手):老师,不可以,小熊要20元,我只有10元钱,钱不够,10元只够买皮球和乒乓板。
师(开心):如果允许你买其他的东西,你能算算还欠几元吗?
生5:老师,我买飞机,40元-10元=3元,还欠3元
生4:老师,他算错了!(老师示意生4回答)应该是欠30元,40元-10元=30元,(生7脸红了)。
生6:老师,我想买机器人,但是我算不来。
师:谁能帮帮他?
生7:45元-10元=25元
生8:错了错了
师:哪里错了?
生8:算错了,应该是35元。
……
在这里,且不论这样设计是否妥当,让人疑惑的是学生为什么“不会算”。在我们看来,这属于生活经验,没有什么难度。为什么不会算呢?刚开始,还认为是教师教法不得法,学生不认真学习造成的。可事实恰恰相反。课后询问学生得知类似于这样不会算或是算得慢的学生并不是个别现象,而是有一大部分的学生存在。
此后,更就此现象询问部分曾经上过此课的老师们,据他们回忆,这样的“不会算或算得慢”的问题或多或少都存在。究竟是什么原因也说不上来,只是认为这种生活中常见的题不会算,是一件意想不到的事,也没在意。笔者也相当疑惑,也就此翻阅了大量的资料,可资料上对此也无从解释。
二、解决:歪打正着,原来是这样啊
一个偶然的机会,笔者执教了一年级。因为公开课的需要,无意之间把第六单元“100以内的加减法”提前上了,回过头才教本单元。惊奇地发现,课堂上“不清楚”“不会算”的问题根本没有出现,甚至以前课堂上认为的一些难点也很快得到解决。这种现象让人觉得奇怪,同样的教法,为什么会有不同的效果呢?是学生不同的原因吗?是教师教法熟练的原因?还是偶然?
于是又在不同的学校,请不同教师像这样调换顺序上,惊喜地发现原来共同疑惑的问题没有了,而且学生对各个知识点接受起来还特别快。带着这种疑惑,笔者联合老师们重新研究了教材、教参,又对学生再一次进行调查研究,才恍然大悟!原来如此。学生之所以有不会算的现象,那是因为45-10等题目是属于100以内的加减的范畴,对于没学过的知识算得慢或不会算是正常的。
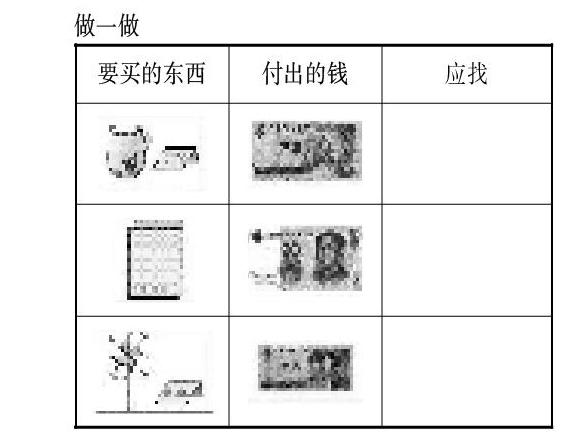
又仔细研究了教材中这个例题,发现计算处处有100以内加减法的痕迹:45-30 40-10 20-10等等都属于100以内不退位减法。再如同页做一做中(如上图)“风车0.50元,付出2元,应找多少?”的计算也是2元-0.50元=20角-5角=15角,绕了几个弯,归根结底也是100以内退位减法。像这样的题目有很多,课本第55页的第10、11题以及作业本的练习题都是同样的类型。敢问大家,没学过的知识如何让学生灵活应用呢?就算个别学生会熟练算,那也是个别例子,再加上没有学过100以内加减法的知识,计算发生困难是在所难免的。
三、深入:集思广益,我们还可以怎样做
问题的症结找到了,解决自然是水到渠成。但是,并不满足这一问题的解决,在思考计算这一单元提前教学只对本例题有益吗?会对本单元其他知识点教学产生帮助吗?带着这样的思考,再次打开课本,寻找以前学生不易理解的例题,对它们重新定位思考。讨论中又有了意想不到的收获。
例5和做一做1(如左图)学习单位间换算,引导学生认识和理解进率关系,关于这点学生总是错误百出。像“26角=( )元( )角”从小单位到大单位的换算题,按照原来教法,需要明白“先把26角分成20角和6角,其中20角等于2元,6角不换算,两者合起来是2元6角”这一长串的原理,学生是记得云里雾里。在整个单位换算过程中,学生需要理解两个概念:一个是人民币的换算,另一个是整十数加一位数的算法和算理。学生在不熟悉计算的基础上,还要绕两个弯,效果自然不理想。如果现在用“20+6”这样整十数加一位数的算法和算理来解释是不是会很清楚呢?同理,像“3元8角=( )角”这样从大单位到小单位的换算题,用几个十加几个几的方法来理解的话,学生对几个几这样抽象的概念不易理解,用难点去理解难点无疑是雪上加霜,到后来只能死记硬背。但学习了第六单元后,运用30+8方法去解决,就容易接受了。
再如例7(右图)是关于元、角的加法计算,属于综合题,包括“认识小数标的物体单价、加法的含义、100以内加法的计算、人民币的单位换算”四个知识点。计算“1.20元+1.20元=12角+12角=24角=2元4角”之类的题目,一直以来是教学难点。我们对此争议很大,因为要经历3个阶段的换算:第一阶段“1.2元=12角”,第二阶段是100以内的加法“12角+12角=24角”,第三阶段才是“24角=2元4角”。这三个环节中,有一个环节不熟练就会造成结果错误。虽然后来教参对此不做考试要求,在一定程度上减轻了教师压力,但每次遇上它,心里还是忐忑不安。如果学生熟练了两位数加一位数进位或不进位加法后,这个问题就不是那么难了,可以说是很容易解决的一个问题,甚至还可以适当拓展题目的应用范围。
在大家的共同努力下,问题不但顺利解决了,而且还有一些意外收获。“忽以问小而不究”,对于这样一个小问题,就算不注意它甚至放过它,可能对整个一年级的教学起不了多大影响。但我们心知肚明,问题长期积累不解决对学生个人发展是极其不利的。新课标提倡“人人学有价值的数学,人人都能获得必需的数学,不同的人在数学上得到不同的发展”不就成为一句口号?因此在教学中,做一个有心人,多问自己几个“为什么错了”是必要的,问题的出现不管大小都不是偶然的,都有其存在的必然性。这其中牵涉很多学生对算理算法的不理解,及时发现,及时找原因找方法解决,于学生学习有益,于教师本身更有益。
同时也要注意解决方法,只靠一个人埋头苦干苦思是不行的。尤其对新手来说,探索和反思往往难以到点子上,一个人,要走很多弯路。这段路我们都走过,老师痛苦,学生也痛苦。要认真钻研,也要学会集思广益,多请教同行、专家,以期经验及时交流共享。现在科技那么发达,建立一个交流平台如QQ、微信,进行微信教研,天南地北可以随时随地“请教”。总而言之,做一个教学有心人,“问小也需究”,肯定更上一层楼。
参考文献:
课程教材研究所.教师教学用书[M].北京:人民教育出版社,2014.

