基于贝叶斯正则化算法BP神经网络钒电池SOC预测
杨春生 牛红涛 隋良红 李明兴
摘 要: 电池荷电状态(SOC)用于表征电池的剩余电量,是全钒液流电池的一个重要参数。在此介绍常用的钒电池SOC预测方法,并对比其优缺点。基于电池SOC的非线性特征,提出采用BP神经网络预测钒电池的SOC,并采用L?M优化算法以及贝叶斯正则化算法对网络进行优化。使用贝叶斯正则化改进的神经网络在对项目中全钒液流电池测试过程实时预测SOC。实验结果表明,采用贝叶斯正则化算法改进的神经网络能够提高SOC的实时预测精度,具有很好的实用前景。
关键词: 钒电池; 荷电状态; BP神经网络; 贝叶斯正则化算法
中图分类号: TN915?34; TP301.6 文献标识码: A 文章编号: 1004?373X(2016)08?0158?04
Application of BP neural network improved by Bayesian regularization algorithm in VRB SOC prediction
YANG Chunsheng1, NIU Hongtao1, SUI Lianghong1, LI Mingxing2
(1. National Institute of Measurement and Testing Technology, Chengdu 610021, China;
2. School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610064, China)
Abstract: The state of charge (SOC) is an important parameter of VRB to character the remaining capacity of the battery. In this paper, the common prediction methods of VRB SOC are introduced, and the advantages and disadvantages are compared. Based on the nonlinear characteristic of VRB SOC, the method of using BP neural network to predict VRB SOC is proposed. The BP neural network was optimized with Levenberg?Marquardt optimization algorithm and Bayesian regularization algorithm. The neural network improved with Bayesian regularization can predict SOC in real time in VRB testing process. The experimental results show that the neural network improved by Bayesian regularization algorithm can improve the real?time prediction accuracy of SOC, and has good application prospect.
Keywords: VRB; SOC; BP neural network; Bayesian regularization algorithm
0 引 言
随着传统化石能源的不断消耗,能源供应已越发紧张,燃烧化石能源带来的环境问题已经给国民经济发展带来严重负担并威胁国民健康。调整能源结构已迫在眉睫,国家也制定了一系列的政策措施,推动新型可再生能源的发展。大规模储能设备是风能等新型清洁能源存储、输送的关键设备,近年来一直是研究重点。全钒液流电池是一种根据钒离子价态改变进行能量交换的一种液流电池,有望在今后大规模储能领域扮演重要角色。电池荷电状态(SOC)是电池管理的一个重要参数,表征电池放电的剩余电量。电池SOC在电池放电过程中受到电池端电压、电流、电池内阻以及电池温度的影响[1]。在钒电池测试工作过程中,实时有效地监控钒电池的SOC状态,对于提高钒电池的电化学性能和安全性能具有重要意义。
1 钒电池SOC常用预测方法
电池SOC不能够直接测量,只能够通过测量某时刻电池其他参数估计得到[2]。常用于预测电池SOC的方法包括:安时积分法、开路电压法、内阻法、卡尔曼滤波法和神经网络法。安时积分法通过对电流进行积分求得放掉的电量。电池初始时刻的电量减去电池放出的电量,即为电池剩余电量。这种估计方法只考虑了电流的影响,忽略了很多因素的影响,其缺陷是无法准确知道初始时刻的荷电状态以及存在误差积累问题[2?4]。开路电压法是根据电池的SOC与电池开路电压存在一定的联系。通过测多个点进行曲线拟合,得到SOC与开路电压的关系。这种方法算法简单,但是开路电压与工作电压不同,两者的差别受到电流引起的极化效应影响,因此无法在电池工作时动态测量SOC[5]。内阻法由于电池的内阻非常小,而且在电池动态工作时候,很难测量[6],不易推广。卡尔曼滤波法需要建立一个高精度的电池模型才能达到预测精度[6?7]。神经网络法具有非线性的基本特征,有很强的学习能力。根据Kolmogorov定理,一个三层前向网络具有对任意精度连续函数的逼近能力[8]。因此,使用神经网络预测钒电池SOC具有明显的优势。
2 BP神经网络结构和原理分析
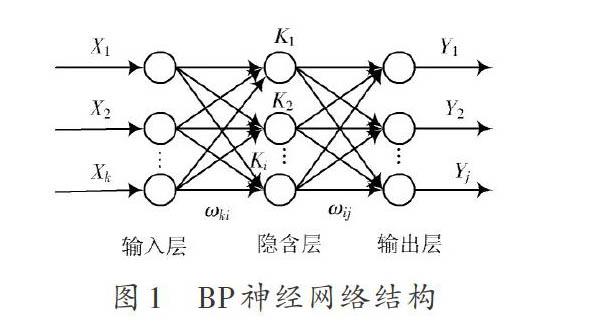
BP(Back Propagation)神经网络是一种按照误差逆传播算法训练的多层前馈网络,广泛应用于非线性逼近[9]。如图1所示,BP神经网络结构包含输入层、隐含层和输出层三个层次。网络在层与层之间是全连接的,每一层神经元之间无连接。输入层和输出层的神经元个数由具体要求确定。隐含层节点数对网络性能影响较大,增加节点,可以提高网络的性能,但训练时间较长。目前仍然是根据经验确定隐含层节点数,通常在5~15之间。
原理算法上,内部信息处理集中在网络隐含层。以隐含层的一个神经元K1为例,它的输入值包括输入层神经元的所有输出值的加权和K1神经元的阈值b1。输入的权值[ω11,ω12,…,ωki]和b1是可调整的。神经元将求得的加权和与阈值b1之和通过神经元内的传输函数得到K1神经元的输出结果。隐含层传输函数是一个非线性函数,最常用的是logsig函数或tansig函数,输出层函数可以是线性函数purelin函数[10]。
标准的BP神经网络采用最速梯度下降法训练网络。训练过程包括信号的正向传递和误差的反向传递。信号通过各层的神经元之间的传递,最终得到网络的输出值。训练网络时除了需要原始的输入数据外,还需要一个目标输出结果。每一次网络的输出与目标结果之差视为网络的输出误差。通过以上信号正向传递的分析知道,网络的输出结果以及误差实际上是关于各个权值的函数。网络的第h次迭代的输出性指标以输出误差能量表示:
[e(h)=12j=0Je2j(h)] (1)
式中:J表示输出值个数;ej表示第j个输出与对应目标输出之差。当误差值大于训练设置的目标性能参数时,调整各神经元的输入权值,使得权值朝着最速梯度下降方向调整。这个过程是从后向前逐层调整,直到输出误差达到要求或者设定步数完成为止。这种算法的一大缺点在于网络可能按照梯度下降收敛到某个局部极小值而非全局的最小值。
3 BP网络改进算法和网络建立
3.1 L?M优化算法trainlm[11?12]
L?M(Levenberg?Marquardt)算法可以有效提高BP神经网络的收敛速度和降低预测误差值。L?M算法按照式(2)对网络权值进行迭代。
[ω(h+1)=ω(h)-[JTJ+μI]-1JTe] (2)
式中,[μ]是可以调整的非负数,当误差较小,则减小[μ]值,当误差较大,则增加[μ]的值。由于避免计算Hessian矩阵,大大降低了计算量,因而比起最速梯度下降法,L?M的收敛速度很快,但是L?M算法对于内存的占用更大。
3.2 贝叶斯正则化算法trainbr
Trainbr[13?16]算法是在神经网络训练过程中,在常规均方差性能函数基础上引入对性能函数的修正函数。
[f(ω)=αEω+βEd] (3)
式中:[f(ω)]为修正后的性能函数;[Eω]为网络所有权值的均方误差;[Ed]为网络输出结果均方误差;[α],[β]为正则化参数。网络通过自适应方法自动根据训练结果调整[α],[β]值以调整网络权值。由于[α],[β]参数按照常规方式很难确定,贝叶斯正则化算法思想就是将权值参数设为随机变量,根据权值的概率密度确定最优的权值函数。文献[13?16]对该算法的具体过程步骤做了详细介绍。采用trainbr可以有效改善拟合曲线的误差。
3.3 BP神经网络建立
本文需要预测的是一组由5节单体钒电池串联组成的钒电池组在实际放电过程中的实时SOC值。工作过程中对电池工作温度进行控制,着重考虑温度相同情况下电池端电压和放电电流对SOC的影响,通过Matlab神经网络工具箱建立BP神经网络。输入层神经元为电池电压V输入和电流I输入。输出层只有一个神经元,输出SOC的预测结果。隐含层通过经验公式和实际训练效果确定,当隐含层设为10个节点时比较合理。
在对网络训练之前,需要将训练样本数据进行归一化预处理。数据的归一化操作能够使网络避免由于输入数据量级差异而导致的误差,提高网络的泛化能力。由于此处采用tansig函数作为传输函数,将其输出值限定在(-1,1)之间,所以需要将电压值和电流值都归一化到 (-1,1)内[17]。数据归一化处理计算公式如下:
[xi=2xi-xmin-xmaxxmax-xmin] (4)
式中:[xi]为归一化后的数据;[xi]为原始数据;[xmin,xmax]为初始数据的最小值和最大值。钒电池在正常测试过程中,电池电压在4.5~9 V之间,所以将最小值和最大值设为4.5和9。钒电池单次放电为恒流放电,因此整个过程中电流的最大值和最小值没有差别。考虑电池在多种电流下的恒流放电,以扩展网络预测的工况范围,将电流的最大值设为9 A,最小值设为2 A。这个范围包含了钒电池在40~120 mA/cm2的电流密度区间,涵盖了项目要求的所有测试电流大小。输入的目标值SOC以百分号为单位表示,因此它的最大值是100,最小值是0。
本BP网络的训练样本由三种电流密度下的100组数据组成。一共为300个数据,将电压和电流归一化后,组成一个2行300列的矩阵,作为输入。同时建立三个BP神经网络,设置输入层和隐含层传递函数为tansig函数;输出层为purelin函数,设定输出误差值0.001,学习率为0.05。三个网络分别采用traingd,trainlm和trainbr算法训练。
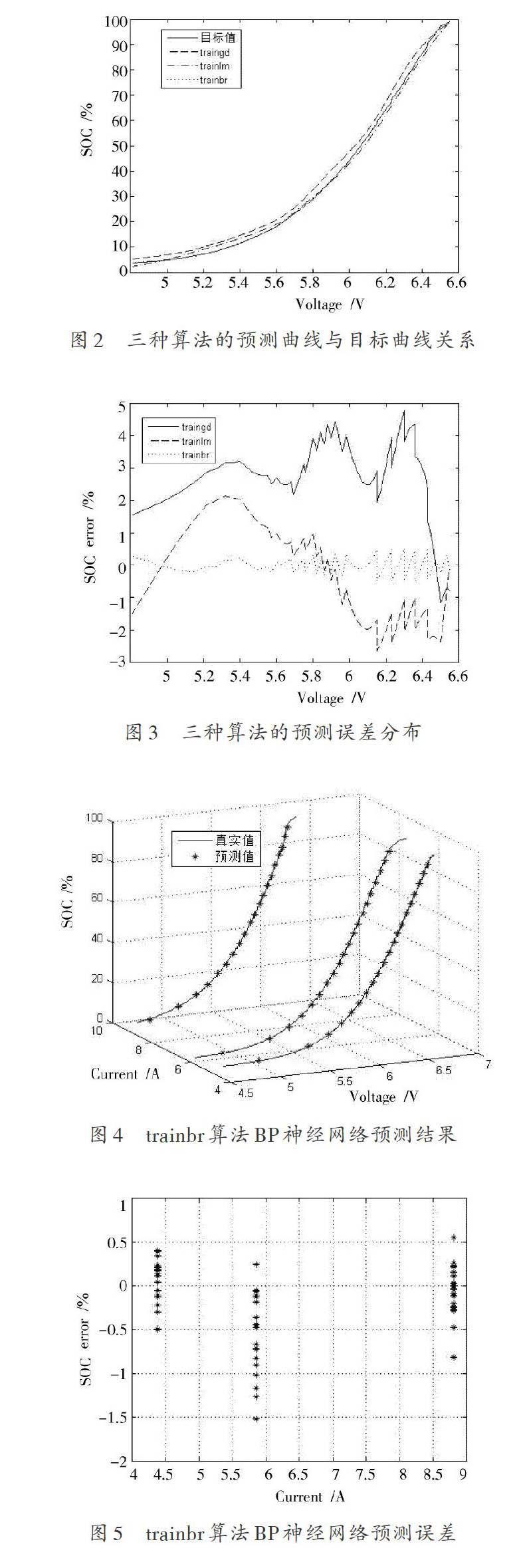
训练的网络对80 mA/cm2电流密度下的样本模拟输出SOC值反归一化到0~100后与目标值的比较结果如图2和图3所示。显然采用贝叶斯正则化算法的模型更好。
4 试验结果与分析
将通过贝叶斯正则化算法训练好的BP网络保存于Matlab安装目录下,钒电池充放电监控系统上位机软件由LabVIEW编写,LabVIEW通过调用Matlab脚本VI调用这个训练好的神经网络,对钒电池在多个不同电流密度下的放电实验进行采样,对每一个采样时刻进行SOC值估计并动态显示。
实验中所测试的钒电池按照电流密度60 mA/cm2、80 mA/cm2和120 mA/cm2,对应电流为4.42 A,5.89 A和8.81 A对电池进行放电测试。电池充放电监控系统每一秒采集电池放电实时端电压和电流值,通过软件归一化后作为网络输入。每一组实验随机抽取了20个预测点,预测结果与其真实值如图4所示,其预测误差值分布如图5所示。
图5中误差分布集中分布在±0.5%,最大误差值-1.5%。
从图2和图3几种曲线的对比看出相比较于标准的最速梯度下降法和常用的L?M优化算法,采用贝叶斯正则化算法训练的网络的逼近结果更能接近真实值。实际上对于L?M算法3%的训练误差,已经可以认为是一个不错的结果,本实验只采用贝叶斯正则化算法而非L?M算法的原因就是,因为经过trainlm算法训练的网络对训练样本实现了较好的拟合,而对于训练样本之外的新样本表现的误差会更大。实际应用中样本不可能将所有预测的结果都包含,否则就不需要再进行预测了。因此本试验需要一个能够具有很好的推广作用的神经网络,能够通过网络对小样本所反映的规律准确的反应。贝叶斯正则化算法训练的神经网络,具有对输入噪声不敏感的特点,因而训练的误差更小,具有更好的推广能力。因此用贝叶斯正则化算法训练好的网络来实时预测电池放电过程中SOC状态比较理想。
5 结 语
钒电池SOC值是表征钒电池放电过程中的剩余电量的一项重要参数,无法直接测试,只能通过多个实时参数对其进行估计。
本文在控制放电温度条件下,分析了常用三层BP神经网络对于SOC非线性曲线逼近的原理,在参考了L?M算法对BP网络优化的基础上,提出运用贝叶斯正则化算法训练改进BP网络应用于钒电池SOC的预测。对比通过训练样本的训练结果,证明贝叶斯正则化算法的训练结果更优。运用该算法训练的神经网络作为预测工具,对钒电池多个放电电流情况下实时SOC值进行实时动态预测。结果显示,预测绝对误差低于±2%,证明方法是准确可行的。
参考文献
[1] 万永凯.混合动力电动汽车锂离子电池SOC估计方法研究[D].武汉:武汉理工大学,2013.
[2] 杜涛,李爱魁,马军,等.动力电池SOC预估方法研究进展[J].电源技术,2015,39(4):844?845.
[3] 王熙俊,张胜寒,张秀丽,等.全钒液流电池SOC监测方法综述[J].华北电力技术,2015(3):66?70.
[4] 林成涛,王军平,陈全世.电动汽车SOC估计方法原理与应用[J].电池,2004,34(5):376?378.
[5] 周晓凤,赵又群.电动汽车动力电池SOC估算研究[J].机械科学与技术,2014,33(2):263?266.
[6] 李国进,董第永,陈双.磷酸铁锂电池的SOC预测[J].计算机仿真,2015,32(3):163?168.
[7] 李正国,孟凡琨.SVM和Kalman滤波大功率动力电池SOC预估方法的研究[J].中国测试,2013,39(5):92?95.
[8] SHI P, BU C G, ZHAO Y W. The ANN models for SOC/BRC estimation of Li?ion battery [C]// Proceedings of 2005 IEEE International Conference on Information Acquisition. [S.l.]: IEEE, 2005: 560?564.
[9] 周品.Matlab神经网络设计与应用[M].北京:清华大学出版社,2013.
[10] 陈明,武冬,郅晓娜,等.Matlab神经网络原理与实例精讲[M].北京:清华大学出版社,2013.
[11] 苑倩,刘金枝,杨鹏.基于BP神经网络的锂电池SOC在线预测[J].河北工业大学学报,2014,43(5):15?20.
[12] 尹安东,张万兴,赵韩,等.基于神经网络的磷酸铁锂电池SOC预测研究[J].电子测量与仪器学报,2011,25(5):433?437.
[13] 杨海深,傅红卓.基于贝叶斯正则化BP神经网络的股票指数预测[J].科学技术与工程,2009,9(12):3306?3310.
[14] 杨琴,谢淑云.BP神经网络在洞庭湖氨氮浓度预测中的应用[J].水资源与水工程学报,2006,17(1):65?70.
[15] 田凯,孙永泰,高慧,等.贝叶斯算法BP神经网络缺陷量化研究[J].中国测试,2014,40(3):93?97.
[16] 宋雷,黄腾,方剑,等.基于贝叶斯正则化BP神经网络的GPS高程转换[J].西南交通大学学报,2008,43(6):724?728.
[17] 蔡信,李波,汪宏华,等.基于神经网络模型的动力电池SOC估计研究[J].机电工程,2015,32(1):128?132.

