基于FilterPro的有源滤波器的快速设计与分析
张涛 郑大威

摘 要: 在当今的电信设备和各类控制系统中,滤波器应用极为广泛,滤波器的优劣直接决定产品的优劣,其中有源滤波器的应用更为灵活和方便。针对有源滤波器两种常见的拓扑结构:多路反馈型(MFB)和压控电源型(Sallen?Key),对两种滤波器的传递函数进行推导和分析。利用德州仪器公司的滤波器设计软件FilterPro,按照两种拓扑结构设计基于巴特沃斯的有源滤波器,并用Multisim 14对设计的两种滤波器进行仿真和验证,为今后有源滤波器的设计与应用提供一定理论基础。
关键词: 有源滤波器; MFB; Sallen?Key; 拓扑结构; FilterPro; Multisim 14
中图分类号: TN713.8?34 文献标识码: A 文章编号: 1004?373X(2016)08?0115?03
FilterPro?based rapid design and analysis of active filter
ZHANG Tao, ZHENG Dawei
(Institute of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430000, China)
Abstract: The filter is widely used in present telecommunication equipments and various control systems. The advantages and disadvantages of the filter directly decide the quality of the products. The application of the active filter is more flexible and convenient. For the two common topological structures (MFB and Sallen?Key) of the active filter, the transfer functions of the two filters are derived and analyzed. The filter design software FilterPro made by Texas Instruments is used to design the active filter based on Butterworth according to the two topological structures. The designed two filters are simulated and verified by means of Multisim 14, which provides a certain theoretical basis for the design and application of the active filter in the future.
Keywords: active filter; MFB; Sallen?Key; topology structure; FilterPro; Multisim 14
0 引 言
对于现代电子技术,滤波器作为信号处理中基础并且重要的电路单元,在许多领域都得到了广泛的应用,其中应用更为灵活的要属有源滤波器。有源滤波电路一般由RC网络和集成运放组成,因而必须在适合直流电源作用下才能正常工作。在信号处理的过程中,不仅没有损耗,而且还可以放大信号,负载效应不明显,多级相联时前后级影响很小,因此利用级联的方法很容易构成高阶滤波器。由于理想滤波器的特性难以实现,因而都是按某个函数形式来设计,常用的有巴特沃斯型、切比雪夫型、椭圆函数型、贝塞尔型等;按照常见的电路拓扑结构分类,可分为无限增益多路反馈型(即MFB型)和压控电压源型(即Sallen?Key型)。根据不同的实际应用要求,选择相应的滤波函数和滤波器拓扑结构,按照相应指标进行滤波器参数的计算过程繁琐,计算量大,而利用德州仪器公司有源滤波器设计软件FilterPro辅助完成有源滤波器设计,可以大大提高有源滤波器的设计效率。
1 MFB型滤波电路分析
常用MFB型有源滤波器根据通带范围有低通、高通、带通、带阻和全通滤波器,如图1所示为二阶低通滤波器,对无限增益多路反馈型电路的特点进行分析:信号由运放的反相端输入,输出端通过R4,R5构成反馈支路,反馈的强弱与输入信号的频率f有关。由于理想运放的增益为无穷大,因此称之为无限增益多路反馈滤波器。增加RC环节后,滤波器的过渡带变窄,衰减斜率增大。
1.1 传递函数的推导
由图1可知,理想电压的放大倍数为:
[A=-R4R1] (1)
根据运放的理想分析条件:U+=U-;I+=I-=0;以及节点电压法,对于以上电路进行分析:
[UA-UiR1+UAsC2+UA-UoR4+UAR3=0] (2) [UAR3+UosC5=0] (3)
解得:
[UiUo=-1R1R3C2C5s2+1C21R1+1R3+1R4s+1R3R4C2C5] (4)
故该MFB型二阶有源低通滤波器传递函数为:
[H(s)=A1R3R4C2C5s2+1C21R1+1R3+1R4s+1R3R4C2C5]
考虑到二阶低通滤波器传递函数标准形式为:
[H(s)=Aωc2s2+ωcQ?x+ωc2]
所以:
[ωc=1R3R4C2C5;Q=R1R3R4+R1R4+R1R3?R3R4C2C5]
1.2 滤波特性的分析
根据以上电路的分析和对传递函数的推导,可知MFB型滤波电路从反相端输入,具有倒相作用,并且使用元器件较少,但是其截止频率[fc=12πωc=][12π1R3R4C2C5]与增益A有关,故增益调节不方便。
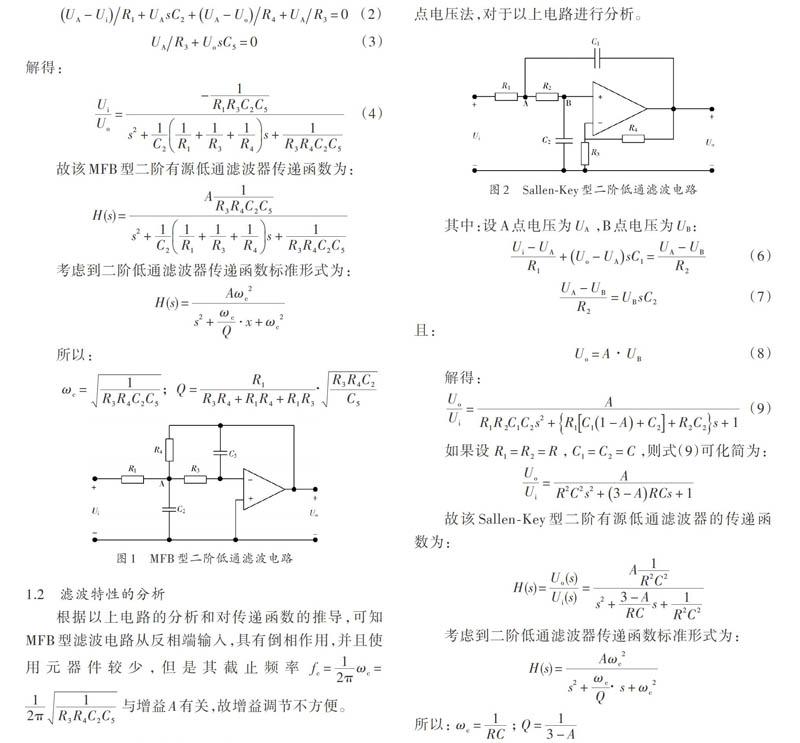
2 Sallen?Key型滤波电路分析
常用Sallen?Key型有源滤波器根据通带范围有低通、高通、带通、带阻和全通滤波器,如图2所示为二阶低通滤波器,对压控电压源型电路的特点进行分析:信号由运放同相端输入,输入阻抗很高,输出阻抗很低,滤波器相当于一个电压源,因此称之为压控电压源滤波器。二阶压控电压源有源滤波器中的一个电容C1原来是接地的,现在改接到输出端,不影响通带内的增益。
由图2可知,理想电压的放大倍数为:
[A=1+R4R3] (5)
根据运放的理想分析条件:U+=U-;I+=I-=0;以及节点电压法,对于以上电路进行分析。
其中:设A点电压为UA ,B点电压为UB:
[Ui-UAR1+Uo-UAsC1=UA-UBR2] (6)
[UA-UBR2=UBsC2] (7)
且:
[Uo=A?UB] (8)
解得:
[UoUi=AR1R2C1C2s2+R1C11-A+C2+R2C2s+1] (9)
如果设[R1=R2=R],[C1=C2=C],则式(9)可化简为:
[UoUi=AR2C2s2+3-ARCs+1]
故该Sallen?Key型二阶有源低通滤波器的传递函数为:
[H(s)=Uo(s)Ui(s)=A1R2C2s2+3-ARCs+1R2C2]
考虑到二阶低通滤波器传递函数标准形式为:
[H(s)=Aωc2s2+ωcQ?s+ωc2]
所以:[ωc=1RC];[Q=13-A]
根据上述传递函数推导可知,二阶Sallen?Key型有源低通滤波器的通带增益易调节,但是只有当增益A小于3时才能保证电路稳定工作,当A趋近于3时,品质因数Q趋近于无穷大,有源滤波器自激振荡。
3 有源滤波器的快速设计
德州仪器公司的FilterPro有源滤波器设计软件提供一种新的、改进的用户接口界面,以及更精确、更稳定的有源滤波器设计引擎。FilterPro有源滤波器设计工具允许设计者通过滤波器设计向导轻松地创建和修改滤波器设计。另外,用户还可以调整元件的误差来观察响应的变化,还可以查看和导出滤波器的性能数据至Excel。下面分别对上述分析的两种滤波器进行设计。
3.1 MFB型二阶有源低通滤波器快速设计
(1) 选择滤波器类型为Lowpass,如图3所示。
(2) 设定滤波器的参数:截止频率fc=1 000 Hz,增益A=2,阶数为2,如图4所示。
(3) 选择滤波函数为Butterworth,如图5所示。
(4) 选择滤波器拓扑结构为Multiple?Feedback,如图6所示。
(5) 点击Finish完成设计,得到电路图及元器件参数如图7所示。
3.2 Sallen?key型二阶有源低通滤波器快速设计
同MFB型二阶有源低通滤波器的设计流程一致,仅在滤波器拓扑结构选择时选择Sallen?key型,得到电路及元器件参数如图8所示。
4 有源滤波器的仿真分析
依据以上两种拓扑结构的滤波器设计结果,选用超低失调电压双路运算放大器OP07Z,在Multisim 14软件中对其滤波特性进行仿真分析。MFB型二阶有源低通滤波器幅频特性响应曲线如图9所示。Sallen?key型二阶有源低通滤波器幅频特性如图10所示。由图9和图10可以看出,两种拓扑结构的低通滤波器在通带内平坦,截止频率也能达到要求,但是Sallen?key型滤波器的高频截止特性不好,原因在于图8中C2横跨在输入与输出之间,对于高频信号,运放的增益很低,此时运放基本不起作用了,输入信号直接越过C2到达了输出端。
5 结 语
本文以巴特沃斯二阶低通滤波器为例,分别对MFB和Sallen?key两种常用有源滤器拓扑结构的传递函数进行推导,并且利用德州仪器公司的滤波器设计软件FilterPro完成快速设计,并在Multisim 14上进行仿真验证。本文对于实际设计,根据要求合理快速地进行滤波器设计,具有一定参考价值。
参考文献
[1] 森荣二.LC滤波器设计与制作[M].薛培鼎,译.北京:科学出版社,2005.
[2] 牛燕炜.有源低通滤波器的设计与仿真分析[J].现代电子技术,2007,30(12):181?183.
[3] 徐亮.一种有源低通滤波器的设计与应用[J].电子技术与软件工程,2015(14):149.
[4] 侯卫周,谷城.压控电压源二阶低通有源滤波电路设计与仿真[J].实验技术与管理,2014(10):103?106.
[5] 余丹.有源低通滤波器设计[J].电子技术与软件工程,2014(2):268.
[6] 方明志,佘世刚,周毅,等.锁相环有源滤波器设计及其对参考杂散的影响[J].现代电子技术,2014,37(9):73?76.

