对两道中考探索类试题的反思

李正球

探索类试题是一种重在探索的解答题.其特点是条件或者结论呈现不明显，需要学生自己去探索，可能是由条件探索结论，也可能是由学过的结论去探索一个新的结论，具有开放性.学生在解题过程中需要具有探索精神和创新意识，运用平时所积累的数学经验以及基本思想方法，独立地解决问题.近年来，江苏和南京的中考数学试题常常出现探索类试题，而学生解答的结果却不是很好.本文借助两道探索类试题，从探索类试题的类型，学生解题错误的原因这两个方面出发，着重谈一谈教师在日常教学活动中如何有效地开展探索活动，从而提高学生的探索能力和解题能力.

一、探索类试题的特征

近年来，探索类试题常见的形式有如下几种：

1.给出条件，没有明确结论，需要学生探索结论并加以验证和证明

例1 （江苏省2009年中考试题第26题）

（1）观察与发现

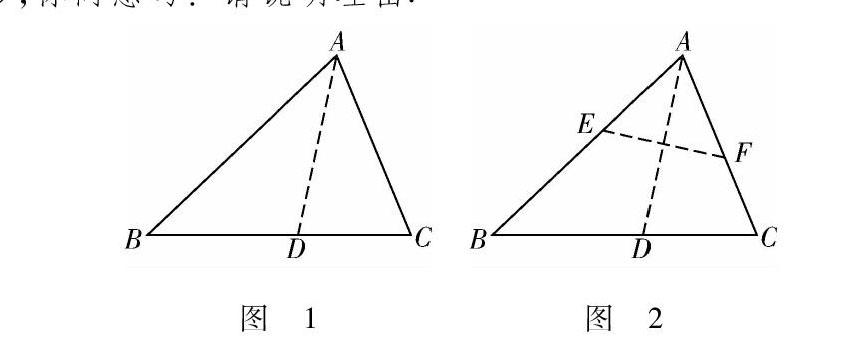
小明将三角形纸片ABC（AB>AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图1）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图2）.小明认为△AEF是等腰三角形，你同意吗？请说明理由.

（2）实践与运用（略）

2.用学过的知识迁移出一个新的知识，学生利用已有知识去探索、归纳出新知识

例2 （南京市2010年中考试题第26题）学习《图形的相似》后，我们可以借助探索两个直角三角形全等的条件所获得经验，继续探索两个直角三角形相似的条件.

（1）“对与两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等”.类似地，你可以等到：“满足 ，或 ，两个直角三角形相似”.

（2）略

二、学生解题错误的主要原因及分析

1.审题问题

审题错误是学生在解探索类试题中错误的主要问题之一，在上述两个类型中都有反映.对于文字较多的题目，学生常常审题不清.一方面学生看见文字多的第一感觉是题目一定很复杂，再加上探索类试题常常出现在中考试卷的最后三题，学生会产生畏惧感，从而导致审题错误.

2.数学语言薄弱

有一部分学生在日常学习过程中由于不注重归纳、总结课本上的数学知识，只知其意，而不能将数学知识用准确、规范的语言表述出来，导致了学生解题错误.

3.缺乏基本的数学思想方法和基础的解题经验

学生不能通过类比、转化等数学思想分析解决问题，缺少解题的基本经验，这也是学生解探索类试题的障碍之一.

三、解探索类试题的教学策略

针对上面阐述的学生解探索类试题的错误原因，笔者谈一谈在日常教学中，教师应当如何提高学生解决探索类试题的能力.

1.解探索类试题的常用方法

解探索类试题的关键是在理解题意的基础上，发现到解题的方法和思路.因此日常教学中，教师必须重视培养学生的解题方法和技巧.以下是解探索类试题常用的几种方法：（1）特殊值法：利用特殊值，进而归纳、概括由特殊到一般，从中找寻规律；（2）类比法：由一个命题的结论猜想出另一个类似命题的结论并加以证明；（3）分类讨论法：当命题的结论不唯一时，要按命题中可能出现的情况分门别类地加以讨论求解.

2.用联系的观念来传授数学知识和思想方法

数学这门学科的一大特点就是知识之间的联系是很紧密的，思想方法的培养始终渗透在日常的教学中.一方面我们要用联系的观念来传授知识，另一方面，我们应当把思维能力的训练贯穿于知识和思想方法的形成之中.

3.强化数学语言的准确性和规范性

首先，丰富学生的数学语言.数学是从数和形的角度对客观事物进行研究的，形式化、符号化、模型化是数学研究的主要特征.其次，强调数学语言的准确和规范，课堂上让学生多举些反例，体会数学语言的准确性和严谨性.

4.关注课本练习，注重变式训练

在平常的教学中，我们一定要立足课本，重视、强化对课本例题、习题的研究，注重引导学生对课本习题进行一题多解、一题多变，将课本习题进行组合、变式、引申，使学生切实体会到加强课本习题研究的重要性，真正做到“以教材为本”，提高学习效率.

5.要强化基础经验的积累

如何在实践教学中帮助学生进行有效地积累数学活动经验这一问题，是值得我们数学教师研究的问题.如在学习知识的同时如何感悟数学思想方法，通过对试题的分析、思考、总结，学生就可以有的放矢的解决问题，并内化为经验，进而自觉的应用.

教师要想提高学生解探索类试题的能力，绝非一朝一夕的事情.在初中三年时间里，教师在传授数学知识的同时，要不断地培养学生的数学思想，积累解题经验，逐步提高解题能力.