Simulations of Transonic Flows withFriction and Heat Addition
William E. Tavernetti, Mohamed M. Hafez
(University of California Davis, USA)
Simulations of Transonic Flows withFriction and Heat Addition
William E. Tavernetti*, Mohamed M. Hafez
(University of California Davis, USA)
The reactive fluid dynamics of transonic flows in nozzles is an important area of experimental and theoretical research. This paper consists of two parts. In the first part an algorithm for the solution of the Euler Equations in conservative form is discussed which simplifies a generalization of Murman Scheme [1] that is presented in Reference [2]. Chattot’s work is discussed and calculations for flows with shocks are presented. In the second part, transonic flows with friction, heat addition and dissipation is considered. Specific attention is given to detonations with one-step Arrhenius chemistry. A part of this study is to understand the interaction between friction and transonic flow with combustion. The details of the numerical algorithms will be presented along with validation examples from the literature.
Numerical algorithms, Computational fluid dynamics, Combustion, Euler equations, Friction, Heat, Compressible
0 Introduction
Numerical solution of Euler equations in conservative form is discussed in Reference [2] using a generalization of Murman Scheme [1]. In [3], Chattot constructed four operators for subsonic, supersonic, sonic and shock points using eigenvalues and eigenvectors of the Jacobian matrix and the compatibility relations to solve the conservation laws of a perfect gas in a convergent divergent nozzle. In this paper, a simplified scheme is introduced and the calculations for flows with shocks are presented. In the second part of the paper, compressible flow with friction and heat addition is considered followed by steady and unsteady detonation.
1 Numerical Method

(1)
Thepresentnumericalschemeisatwo-stepmethod.Centraldifferenceschemeisusedinthesubsonicregionsandatthesonicpoints,backwarddifferenceisusedinthesupersonicregions,withaspecialshockpointoperatoratshockpoints.Theschemeisconservativealmosteverywhereand,unlike
Chattot’s calculations, no special sonic point operator is used in this work. The finite difference formulas and their stencils are shown in Figs.1-3.
1.1 Transonic Flow Examples and Comparison with Lax-Wendroff Method
A first validation test case shows the sharpness of
the shock, correct location (x=0.82) and flow through the sonic point, see Fig. 4.
Examples in 2D for transonic flow over a thin parabolic arc at incidentM= 0.675 andM= 1.4 are in good agreement with Ni’s, who used second order accurate Lax-Wendroff scheme [4]. In Fig. 5 an Oswatitsch-Zeirep singularity at the root of the shock is observed. The present method shows better resolution of this feature and a sharper shock with higher peak than Lax-Wendroff scheme.

Fig.1 Subsonic/sonic stencil and scheme.
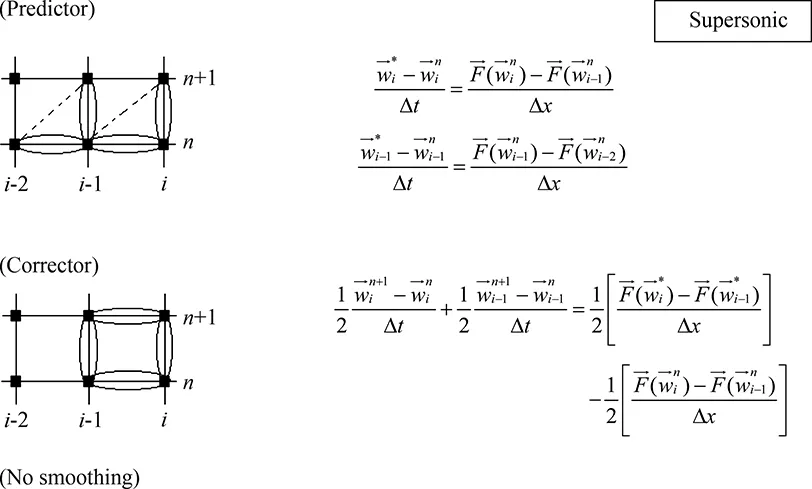
Fig.2 Supersonic stencil and scheme.

Fig.3 Shock point stencil and scheme.
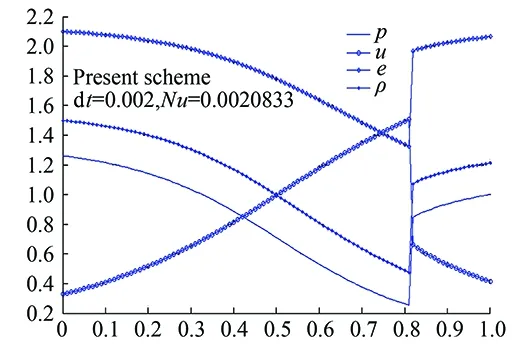
Fig.4 Compressible nozzle flow 1D validation test case.
In Fig.6, a grid refinement study is shown in the case of flow over a thin parabolic arc.
Numerical cases for 2D transonic flow over a circular cylinder are also considered. Comparison with the results of 2-step Lax-Wendroff is shown in Fig.7. The numerical results are in good agreement with the literature [5].
It should be remarked that in the two dimensional calculations, the present scheme is used only in the flow direction, while centered differences, augmented with artificial viscosity, are used for the lateral direction.
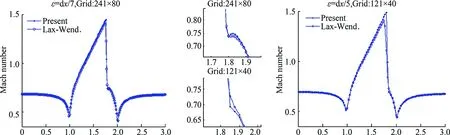
Fig.5 (M∞=0.675) Present vs. 2-step Lax-Wendroff method over thin parabolic arc at different grids.

Fig.6 Grid refinement study for present method showing representative grids of (121×40), (241×80) and (301×100).
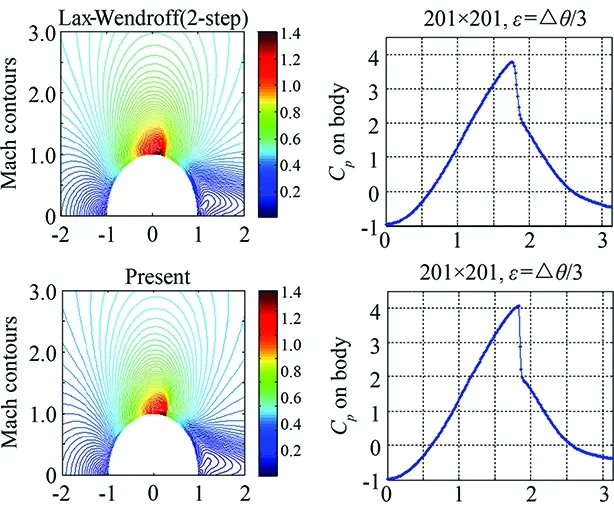
Fig.7 (M∞=0.5) 2D flow over cylinder, comparison of Lax-Wendroff 2-step to present scheme.
1.2 Hypersonic Flow
For a hypersonic flow over a rectangular block is computed for Mach numberM=10. This flow is comparable with the example problem and results published in [6]. In this calculationγ=1.17,the numerical mesh is 88×136 in thexandydirections respectively. Uniform far field boundary conditions are applied , as well as symmetry conditions on the centerline axis. The computational domain is 0≤y≤34. The rectangular body starts atx=18 and the top of the body is aty=12,see Fig.8.

Fig.8 Hypersonic flow over a rectangular block is computed for M=10, present vs. 2-step Lax-Wendroff method.
2 Compressible Flows with Friction and Heat Addition
The Quasi-1D Euler equations with friction and heat addition are given by the conservation laws for mass, momentum and energy respectively:
(Aρ)t+(Aρu)x=0
(2)
(Aρu)+(Aρu2+Ap)x=Axp-f
(3)
(AρE)t+(AρuH)x=q
(4)
Togetherwiththedefinitions:
Asteadycompressibleperfectgasinaductofconstantcrosssectionalareaisconsidered.Therearetwopossibilitiestogetfromtheinitiallysupersonicconditiontothefinalsonicflow:byintroductionoftheheatsourceqor the friction sourcef. For compressible duct flows with friction and heat addition, several formulas are available in terms of Mach number, the friction factor and heat addition, see Reference [7]. Examples of choking due to friction and heat addition are calculated with the present scheme, see Fig.9 and the results are in good agreement with those in Reference [7]. Although the calculation is very sensitive to the amount of heat and the shock moves to the right or the left with slight variation of the critical amount, the shock is very sharp, especially when compared with other artificial viscosity methods, for example Lax-Wendroff scheme.
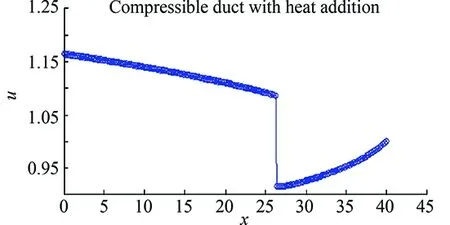

Fig.9 Compressible duct flow 1D with heat addition (up) and friction (down).
3 Steady and Unsteady Detonation
An ordinary differential equation for the species, together with algebraic relations derived from the shock jump conditions gives the steady Zeldovich-Von Nuemann-Doring (ZND) family of solutions to the Euler equations. Although detonations are funda-mentally unstable, the ZND solutions are suitable, in an averaged sense, for many cases. It is shown however by several authors, see for example [8-11], that when solving the Euler equations, the solutions are predicted to be oscillatory and even chaotic for many examples. In general, as the parameterEa, governing the activation energy for the chemical species, is increased, instability increases and the ZND solution becomes less predictive. However, for sufficiently smallEa, the true solution is nearly steady and the correspondence with the ZND solution agrees very well. Detonation in one dimension is governed by the reactive unsteady Euler equations:
(5)
(6)
(7)
(8)
(9)
Wherem,f,qare source terms for mass, friction and heat respectively. The parameterkis a constant factor that relates the reaction and convection rates. The following non-dimensional variables are used:

(10)
Hereudenotes axial velocity component andCf,Mis the coefficient of friction and Mach number respectively. In our calculations:
Q∈[0,50],γ=Cp/Cυ=1.4,Rgas=Cp-Cυ
Incharacteristiccoordinates,intheabsenceofsourceterms,wearesolvingthesystem:
(11)
(12)
(13)
(14)
whereξ=x-st. Initially the shock speedsis given from the ZND theory. Thereafter, the shock speeds=s(t), is corrected for unsteady flow in the characteristic coordinatesξby requiringY=0.5 remain atx=0. LettingLbe a linear operator andNbe the nonlinear reaction operator,w=[ρ,ρu,ρE,ρY],thereactiveEulerEquationscanbewrittencompactlyas:
(15)
Inourcomputationanarticialviscositywithε=O(Δx)isaddedtostabilizethesolutionneartheshock.Weuseanimplicitthirdorderupwindingschemeforconservationofmass,momentumandEnergy
(16)
Tosolvethisstiffsystem,anIMEXoperatorsplittingmethodforthelinearandnonlineartermsinthespeciesequationisused,byupdatingYfirst implicitly with third order upwinding, then explicitly updating the nonlinear terms.

(17)
Severalvalidationcomputationsareperformed,forexamplethesteadystateZNDsolutionwhichisderivedfromthenon-dimensionalizedshock-jumpconditions.Attheshockfrontthefollowingrelationshold:
(ρu)=1
(18)
(19)
(20)
DownstreamoftheshockwethensolveanordinarydifferentialequationforthechemicalspeciesY,
(21)

(22)
TheZNDmodelsetupisshowninFig.10.
HugoniotcurvesforZNDTheoryareshowninFig.11.Asheatisreleased,supersonicflowdeceleratescontinuouslytothesoniccondition,orwecangoalongtheRayleighlinetotheVon-NeumannspikeandthengobackalongthesameRayleighlinetothesoniccondition.
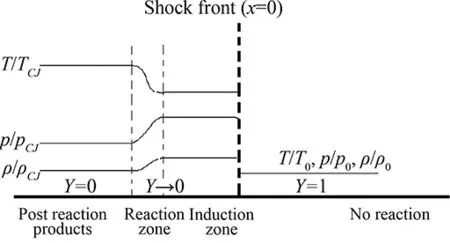
Fig.10 Sketch of ZND solution.
SeveralverificationcomputationsareperformedusingthesteadystateZNDsolutionandareinagreementwithresultsreportedin[12].AnexampleshowingseveralZNDtemperatureprofilesforarangeofEavalues is shown in Fig.12.
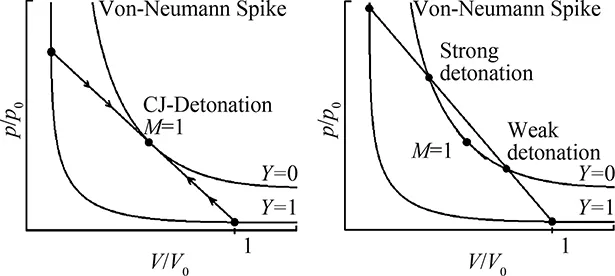
Fig.11 Sketch showing C-J detonation as well as strong and weak detonations.

Fig.12 Several ZND temperature profiles for a range of Ea values.
The third order upwinding method is compared with several ZND solutions for verification. A representative comparison is shown in Fig.13. The ZND solution is computed starting from the shock front while the Euler equations are integrated across the shock starting upstream with unreacted flow.
A Chapman-Jouquet detonation following [13] is computed in Fig.14. We compute the shock speed to bes=5.4419 which exactly matches the CJ-shock speed given in [13]. Additional comparisons with steady state computations are in good agreement with the results reported in [12-14].
The case of friction losses dominating heat transfer effects can sometimes occur when a detonation wave passes through a porous media [14]. In such a case, momentum loss due to friction can be much more influential than heat transfer effects. Following the work of [8] and [11], Fig.15 shows that a source of friction in the momentum equation causes qualitatively the same effect as higherEa.
Our computations show that friction causes a momentum loss which decreases the peak temperature and local velocity, as shown in Fig.16. Increase in the friction causing reduction in temperature was also reported in [8] and [11].
The effect of friction on detonation stability is also considered. TreatingEaas a bifurcation parameter, the peak pressure at the Von-Nuemann state is stored for several simulations as a time
series. The attractor space is then constructed from the local maxima and minima of each time series. Representative examples are shown in Fig.17. In our results, increasing friction causes period doubling for lower values ofEa, this trend is also reported in [8] and [11].
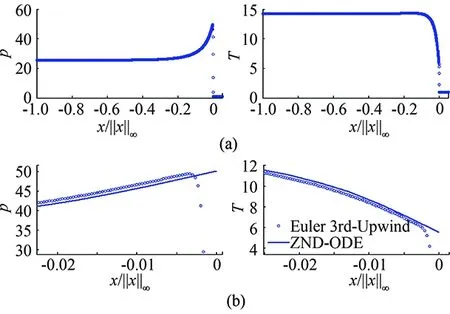
Fig.13 ZND solution by Algebraic/ODE formulation vs.reactive Euler equations. Notice the scale difference between the upper and lower figures to emphasize the difference between the two solutions.

Fig.14 Comparison with C-J detonation.

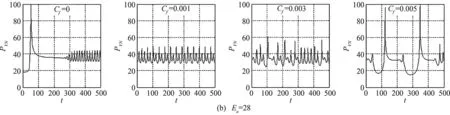
Fig.15 Ea = 25 (top), Ea = 28 (bottom), γ=1.2 showing a range of Cf coeffcients and transition to instability.
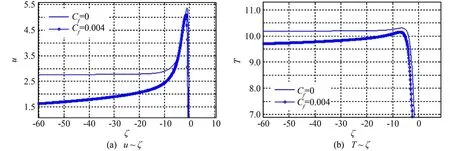
Fig.16 Ea = 23, γ=1.2, comparing Cf = 0 with Cf=0.004, lower temperature, T, and velocity, u, are observed.

Fig.17 Von-Neumann peak pressure for Cf = 0 (left), Cf=0.002 (center), Cf = 0.004 (right),γ= 1.2, showing translation and compression of period doubling regions for variable Ea.
4 Conclusions
In the present work we have demonstrated a simple scheme for computing transonic flows which can be considered as a generalization of Murman’s four point operator to solve the Euler equations. We have examined several transonic steady compressible 1D flows with friction and heat addition. Unsteady flows with weak dissipation and friction have been considered in the context of detonation theory for several reactive compressible cases. Computations with higher order IMEX schemes is also of interest [15].
[1]Murman E M. Analysis of embedded shock waves calculated by relaxation methods[J]. AIAA Journal, 1974, 12(5).
[2]Chattot J J. Computational aerodynamics and fluid dynamics[M]. Springer-Verlag Berlin Heidelberg, New York, 2002.
[3]Chattot J J. A conservative Box-scheme for the Euler equations[J]. International Journal of Numerical Methods in Fluids, 1999, 31: 149-158.
[4]Ni R H. A Multiple grid scheme for solving the Euler equations[J]. AIAA Journal, 1982, 20: 1565-1571.
[5]Hafez Mohamed, Wahba Essam. Inviscid flows over a cylinder
[J]. Comput. Methods Appl. Mech. Engrg., 2004, 193: 1981-1995.
[6]Burnstein S Z. Finite-difference calculations for hydrodynamic flows containing discontinuities[J]. Journal of Computational Physics, 1967,2:198-222.
[7]White F. Fluid mechanics[M]. 6th Edition. McGraw Hill, New York, 2008.
[8]Dionne J P, Ng H D, Lee J H S. Transient development of friction-induced low-velocity detonations[C]//Proceedings of the Combustion Institute, 2000, 28: 645-651.
[9]Romick C M, Aslam T D, Powers J M. The effect of diffusion on the dynamics of unsteady detonations[J]. J. Fluid Mech., 2012, 699: 453-464.
[10]Sow A, Chinnayya A, Hadjadj A. Mean structure of one- dimensional unstable detonations with friction[J]. J. Fluid Mech. 2014, 743: 503-533.
[11]Zhang F, Lee J H S. Friction-induced oscillatory behaviour of one-dimensional detonations[J]//Proc. R. Soc. Lond. A, 1994, 446: 1926: 87-105.
[12]Lee J. The detonation phenomenon[M]. Cambridge University Press, New York, 2008.
[13]Berkenbosch A C. Capturing detonation waves for the reactive Euler Equations[D]. Eindhoven University of Technology, 1995.
[14]Higgins A. Steady one-dimensional detonations[M]//Zhang F. Shock waves science and technology library, Vol.6, Springer, 2012.
[15]Ascher U M, Ruuth S J, Wetton B T R. Implicit-explicit methods for time-dependent partial differential equations[J]. SIAM J. Num. Anal. 1995, 32: 797-823.
0258-1825(2016)02-0175-07
含摩擦和加热的跨声速流动数值模拟研究
William E. Tavernetti*, Mohamed M. Hafez
(University of California Davis, USA)
喷管中跨声速流动的反应流体动力学是实验和理论研究的一个重要领域。本文主要由两部分构成,在第一部分中对文献[2]中的Murman格式[1]的一般形式进行了简化,得到了守恒形式的欧拉方程,并对其求解方法进行了讨论,同时针对Chattot等的工作展开了分析,并给出了带激波的流动计算结果;而文章的第二部分则研究了包含摩擦、加热以及耗散的跨声速流动,并重点关注了一步Arrhenius化学反应模型下的爆震现象。本文还探究了摩擦力和带燃烧的跨声速流动之间的相互作用,同时详细给出了新的欧拉方程数值求解算法并同已有文献算例进行了对比验证。
数值算法;计算流体力学;燃烧;欧拉方程;摩擦力;加热;可压缩
V211.3
A doi: 10.7638/kqdlxxb-2016.0008
*lecturer, Departmant of Mathmatics; etavernetti@ucdavis.edu
format: Tavernetti W E, Hafez M M. Simulations of transonic flows with friction and heat addition[J]. Acta Aerodynamica Sinica, 2016, 34(2): 175-181.
10.7638/kqdlxxb-2016.0008. Tavernetti W E, Hafez M M. 含摩擦和加热的跨声速流动数值模拟研究(英文)[J]. 空气动力学学报, 2016, 34(2): 175-181.
Received: 2015-12-15; Revised:2016-01-10
- 空气动力学学报的其它文章
- Computational Fluid Dynamicsin Europe, a Personal View
- The History of CFD in China
- Coupled CFD/RBD Modeling for a BasicFinner Projectile with Control
- High Order Numerical Methods for LESof Turbulent Flows with Shocks
- Vorticity Dynamics and Control of Self-PropelledFlying of a Three-Dimensional Bird
- Residual Schemes Applied to an Embedded MethodExpressed on Unstructured Adapted Grids

