Computational Fluid Dynamicsin Europe, a Personal View
M. Napolitano
(Department of Mechanics, Mathematics and Management, Polytechnic of Bari, Via Orabona 4, 70125, Bari, Italy)
Computational Fluid Dynamicsin Europe, a Personal View
M. Napolitano*
(Department of Mechanics, Mathematics and Management, Polytechnic of Bari, Via Orabona 4, 70125, Bari, Italy)
This review paper describes some major contributions provided by European scientists to the development of CFD from the early 70s to the end of the 20th century. Particular attention has been paid to those authors who have contributed to the success of the ICNMFD, started in 1969 (Novosibirsk) from a joint effort of scientists involved in the space race in the USA and the USSR, and of the ISCFD, started in 1995 (Tokyo) as a Pacific competitor to the ICNMFD. These two very important biennial international conferences have then merged into the ICCFD, starting from the year 2000, thanks to the efforts of the two scientific committees, promoted by prof. Oshima and the author. The majority of the authors whose work is the subject of this paper have been members of one or more of the Scientific Committees of the three aforementioned conferences, usually after having been selected to provide invited lectures to the same. Their choice is the sole responsibility of the author and is certainly incomplete and biased towards more applied, rather than theoretical CFD. Also, they are often personal friends of the author who has been a member of the CFD community for 40 years. Thus, this paper does not consider younger scientists, independently of the value of their contributions. Moreover, it is noteworthy that European CFD has always been strictly interconnected with US CFD. Some of the authors have started their careers in Europe and are now living and working in the USA (e.g., Glowinski, Roe, Van Leer); others have obtained their Ph.D. in the USA (e. g., Launder, Napolitano), and all of them have worked together with US scientists, so that it is difficult to distinguish between European and US CFD. For those who moved to the USA, their contributions prior to their move have been favored. Last but not least, each of the authors discussed in this work has been asked—by an e-mail that I hope reached them—to write a draft of his own chapter so as to provide the most authoritative review of his contributions. Those who have done so have been duly acknowledged. The other ones will have to forgive the author for an inadequate description of their merits.
Computational fluid dynamics, Direct numerical simulation, Finite difference, Finite element, Finite volume, Flux difference splitting, Flux vector splitting, High-order schemes, Large eddy simulation, Lax-Wendroff scheme, Multigrid, Particle flow, Turbulence modeling
1 Sergei K. Godunov: Everything started with him
Sergei K. Godunov studied at the Department of Mechanics and Mathematics of Moscow State University, where he graduated (MS) in 1951 and obtained a Ph. D. in Physical and Mathematical Sciences in 1954. Sergei started his academic career at Moscow State University and since 1969 at the Sobolev Institute of Mathematics of the Russian Academy of Sciences in Novosibirsk, Russia. In 1976, he became a corresponding member and in 1994 a full member (academician) of the USSR (later Russian) Academy of Sciences. In 1997, on the occasion of the conference organized in his honor by the University of Michigan at Ann Arbor, he obtained an honorary Ph. D. from that University. Godunov obtained the State Lenin Prize (1959), the A. N. Krylov Prize of the USSR Academy of Sciences (1972) and the M. A. Lavrentiev Prize of the Russian Academy of Sciences (1993). Sergei is famous worldwide for having introduced the exact solution of the Riemann problem within a numerical scheme for solving flows with shocks [1], as well as for his theorem, also known as Godunov’s order barrier theorem, which states that Linear numerical schemes for solving partial differ-ential equations, having the property of not genera-ting new extrema (i. e., monotone schemes), can be at most first-order accurate. More about the scientific achievements of Godunov till 1999 are given by his review paper Reminiscences about difference schemes [2]. Since then, Godunov has continued to be active in research, as shown by his many papers published in the new century, see, e. g., [3, 4]. More on Godunov can be found on the Introduction to his work [2] published by Van Leer on the same issue of JCP [5]. A very exhaustive description of Godunov’s method, which has inspired the CFD of flows with discontinuities for 50 years, is provided by Hirsch [6, pp. 444-446]. Here only a sample solution to a shock-tube problem provided by Roe [7] is shown in Fig.1. The solution obtained using the exact Riemann solver is the one provided by Godunov’s method. Roe has shown that there is very little difference between the exact and approximate solvers when used as flux functions.
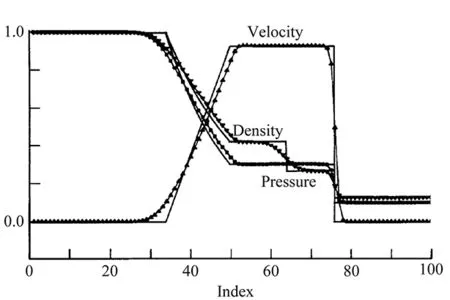
Fig.1 Numerical solution to a shock-tube problem, incorporating either the exact or the approximate Riemann solution in a first-order upwind difference scheme.
2 Massimo Germano: A dynamic subgrid-scale eddy viscosity model
Massimo Germano graduated in Physics in 1965 at the University of Turin. Soon after he became assistant professor in fluid dynamics at the Polytechnic of Turin, where he became full professor in 1980 and served in such a position till his retirement in 2012. He has always had strong contacts with the USA and is now adjunct professor at the Department of Civil and Environmental Engineering, Duke University, Durham NC, USA.
In 1986 Massimo was puzzled over a lot of different interests and many ideas not well defined. He was attracted by the Large Eddy Simulation (LES) of turbulent flows, but mainly from the point of view of a new way to represent them, different from the statistical and the spectral ones. A good friend of his, consulted on the subject, was very skeptical and discouraging: “Please leave that topic, it is unfitted for you. It requires big computers, you are not an expert in numerical and computational problems and there is little space left for new theoretical work”. But for a researcher it is difficult to leave his own suggestions, it is like to abandon a child. In particular Massimo was attracted by some analogies between the classical Leonard formulation of LES and some old ideas of Boussinesq and Reynolds—developed in the middle of the last century by Kampé de Fériet and his school—concerning the rules of the mean from the algebraic point of view; that was the beginning. Following his own ideas, Massimo first produced a paper devoted to the Leonard decomposition, which is based on the sub-grid fluctuations and is not Galilean invariant; thus, he proposed a new one in terms of generalized central moments [8]. These quantities extend the statistical formalism, invariant by definition, to a generic filtering operator. Following this first step, it was easy to derive the multi-scale identity that relates the generalized central moments at different filtering levels, and in 1990 he was sufficiently confident in his new formulation so as to present a research proposal to the annual Summer Program organized at Stanford by the Center for Turbulent Research [9]. That summer at Stanford was very dry, no rain, no water from the fountains,the Lagunita was empty. In a room at NASA Ames, Massimo presented all his work: the operational definition of the generalized central moments, the averaging invariance, and the new decomposition [10, 11]. It was difficult to relate all that to the numerical aspects of LES. Step by step the attention was directed to the multi-scale identity and the related possibility of testing dynamically the Smagorinsky constant at different levels of resolution. The room was hot and the people in the room were immersed in their considerations. Suddenly, some little noise attracted them to the window, it was raining. They gathered again around the table and decided: “Well, let us try”. That was the start of a new life for LES, see [12], which has been cited more than 2880 times (Scopus) and it is the reason why, in the author’s opinion, Germano made a piece of history in CFD. As an illustration, Figs.2 and 3, taken from [12], show how the new dynamic sub-grid scale provides results in much better agreement with filtered DNS than standard LES.

Fig.2 Turbulence intensities 〈ui″2〉1/2 in fully developed turbulent channel flow. (a) u, (b) v, (c) w

Fig.3 Plane-averaged RMS turbulence intensities 〈u″2〉1/2in Re=8000 transitional channel flow. (a) t=176, (b) t=200, (c) t=220
3 Roland Glowinski: Finite element methods and particulate flow
After graduating from Ecole Polytechnique and Ecole Nationale Supérieure des Télécommunications (both in Paris, France), Glowinski took a research engineer position at the French Broadcasting System. In 1968, he moved to the Institut de Recherches en Informatique et Automatique (IRIA) to work on a Ph.D. under the supervision of J.L. Lions (1928-2001). After defending his Ph.D. thesis at the University P. & M. Curie he took an assistant professor position at the above university while being also the leader of a Scientific Computing project at IRIA, and later became full professor. In 1985 he moved to the University of Houston where he obtained an endowed chair that he still holds. Starting in 1972 he moved full time to CFD taking advantage of a close collaboration between Dassault Aviation (J. Périaux and P. Perrier, in particular) and the Institut national de recherche en informatique et en automatique (M. O. Bristeau, O. Pironneau, and Glowinski himself). Through this collaboration, various methods for the numerical simulation of incompressible and compressible flows in two and three dimensions were developed, including finite element approximations, nonlinear least-squares formulations, operator-splitting methods, precondi-tioned conjugate gradient algorithms, leading among other achievements to the first simulation of the transonic flow with shocks of a compressible inviscid flow around a full aircraft, namely, the Dassault Falcon 50. In the mid-eighties, motivated by viscous flow simulations, Glowinski developed [13] a three stage variant of the Peaceman-Rachford ADI scheme (and of the Strang symmetrized operator splitting scheme), called by some practionners the fractionalθ-scheme; this scheme was used by many CFD practitioners, in Germany in particular, and is still used nowadays, thirty years after its discovery. The simulation techniques mentioned above (and much more) are discussed in [13-18], together with numerous applications, including the simulation of viscoelastic and viscoplastic flows. In the mid-nineties, Glowinski (already in the USA) started a collaboration with D.D. Joseph (1929-2011), in order to achieve the direct numerical simulation of the flow of mixtures of rigid solid particles and incompressible viscous fluids, the main ingredients of the simulation methodology being: fictitious domain methods allowing the use of fixed grids, operator-splitting methods to decouple advection, diffusion, incompressibility, and particle motion, the advection being treated by a wave-like equation method particularly easy to implement via finite element methods. Flows with several thousand particles were simulated through this approach, which has been reported in [17] and [19-24], among other publications. Figure 4 shows a cluster formation phenomenon taking place in a rotating cylinder when the angular velocity is beyond a critical value (this phenomenon is further discussed in [24]). Last but not least, Glowinski was awarded the 1996 Grand Prix Marcel Dassault of the French National Academy of Sciences, the 2004 SIAM Theodore Von Krmn Prize, and the 2011 CFD Award of the US Association of Computational Mechanics, for his contributions to CFD. Since 2002 he is fellow of the American Mathematical Society.

Fig.4 Cluster formation for a population of 160 rigid spherical solid particles in a rotating cylinder filled with an incompressible Newtonian viscous fluid. Left: Axial projection of the particles. Right: Visualization of the clusters (operator-splitting/fictitious domain/finite element based methodology).
4 Charles Hirsch: Industrial flows
Charles Hirsch graduated in Enginering from Vrije Universiteit Brussel. He spent his entire academic career at the same University from 1969 to 2005, also as Head of the Department of Fluid Mechanics and he is professor Emeritus after his retirement. Hirsch is President of NUMECA International, since 1993, of NUMECA USA, since 2002, and of NUMFLOW, since 2007. He is the author of one of the most comprehensive textbooks on basic numerical methods and of CFD [6,25]. As demonstrated by his career, Hirsch has always had a strong interest in industrial applications, such as turbomachinery flows [26,27], in which he is among the greatest world experts, and biomechanical applications [28], and has a professional interest for the issue of Verification and Validation (V&V) of CFD codes. Here, only the abstract of [26] and [29] will be reported: “A Navier-Stokes solver is applied to investigate the three-dimensional viscous flow in a low-speed linear compressor cascade with tip clearance at design and off-design conditions with two different meshes. The algebraic turbulence model of Baldwin-Lomax is used for closure. Relative motion between the blades and wall is simulated for one flow coefficient. Comparisons with experimental data, including flow structure, static and total pressures, velocity profiles, secondary flows and voracity, are presented for the stationary wall case. It is shown that the code predicts well the flow structure observed in experiments and shows the details of the tip leakage flow and the leading edge horseshoe vortex” [26]. “The views on the state of the art in V&V in computational physics are discussed. These views are described in the framework in which predictive capability relies on V&V, as well as other factors that affect predictive capability. Some of the research topics addressed are development of improved procedures for the use of the phenomena identification and ranking table for prioritizing V&V activities, and the method of manufactured solutions for code verification. It also addressed development and use of hierarchical validation diagrams, and the construction and use of validation metrics incorporating statistical measures [29].
5 Brian E. Launder: Turbulence modelling
Brian E. Launder received a Bachelor’s degree in Mechanical Engineering from the Imperial College, London, where he came first in the class and won the Bramwell Medal. He then joined the Massachusetts Institute of Technology for his master degree and went on to take a doctoral degree for experimental work on boundary layers. In 1964, he returned to the Imperial College to join the Faculty as Lecturer and later became the Reader in Fluid Mechanics. After serving at the Imperial College for 12 years, Launder went to the University of California, Davis, where he served as Professor of Mechanical Engineering for four years. In 1980 he returned to the UK and joined the University of Manchester Institute of Science and Technology as the Head of the Thermo-Fluids Division, a position he held for 16 years, and where he served two terms as Department Head. Launder’s scientific production is huge and of fundamental importance for CFD. Here the attention will be focused on his cornerstone contribution of 1974 [30], together with D. B. Spalding—another giant of CFD, with whom he had already published the lectures in Mathematical Models in Turbulence [31]. In [30], now cited more than 9000 times (Google Scholar), the authors established the merits of what became the most famous and employed worldwide two-equation turbulence closure, namely, thek-εmodel. Here, the abstract of the paper is reported: “The paper reviews the problem of making numerical predictions of turbulent flow. It advocates that computational economy, range of applicability and physical realism are best served at present by turbulence models in which the magnitudes of two turbulence quantities, the turbulence kinetic energy,k, and its dissipation rate,ε, are calculated from transport equations solved simultaneously with those governing the mean flow behavior. The width of applicability of the model is demonstrated by reference to numerical computations of nine substantially different kinds of turbulent flow”. Thanks to thek-εmethod,Brian,amongmanymorethings,computedtheflownearaspinningdisc[32]andstudiedthegroundeffectsonpressurefluctuationsintheatmosphericboundarylayer[33].AnotherveryimportantcontributionwasinthedevelopmentofaReynolds-stressturbulenceclosure[34],incooperationwithW.Rodi—whoalsoshouldhavedeservedhisownchapterinthispaper.Brianhasmaintainedasteadyandimportantscientificproductionfor50years.Theauthorhadtheprivilegeofbeingoneoftheinvitedspeakersofthe2ndISCFD,Sidney,togetherwithBrian,whogaveamemorablelectureonSecondmomentclosureanditsuseinmodellingturbulentindustrialflow[35],whoseabstractisworthreproducinghere: “Second-momentturbulencemodelfocusdirectlyonthetransportequationsfortheReynoldsstressesratherthansupposingthestressandstrainfieldstobedirectlylinkedviaaneddyviscosity.Thiselaborationenablestheeffectsofcomplexstrainsandforcefieldsontheturbulencestructuretobebettercaptured.Thepapersummarizestheprincipalmodellingstrategiesadoptedfortheunknownprocessesintheseequationsandpresentstheformsthathavebeenfoundmostusefulinengineeringcalculations.Methodsadoptedforovercomingsignificantproblemsofnumericalinstabilityandlackofconvergencecomparedwitheddy-viscosity-basedschemesarealsopresented.Applicationsinvolvingmomentumandheattransferincomplexflowsaredrawnfromtheadvancedtechnologysectorsofpowergenerationandaircraftindustries”.InthefollowingFig.5-7,someresultsfrom[35]areprovided,whichdemonstrateBrian’scontri-butionstoturbulencemodelling.
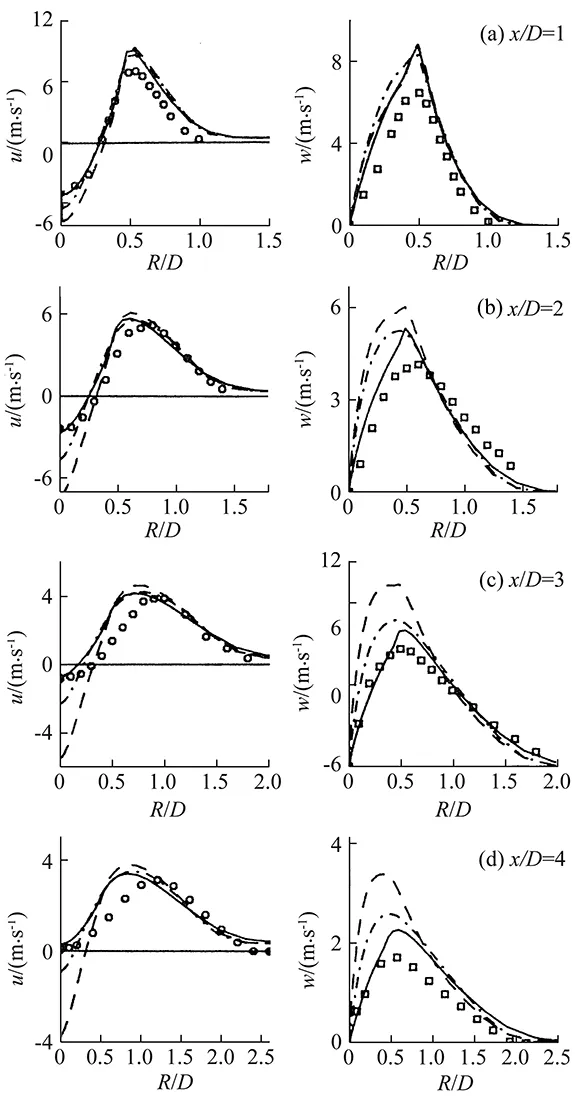
Fig.5 Comparison with experiments of three different models, for the development of the axial □ and swirl ○ components of the mean velocity at four stations of a swirling axisymmetric jet in stagnant surroundings. The convection modified model (IPC) of [35] (solid line) is clearly superior.

Fig.6 Comparison with experiments of the numerical solutions of the velocity profiles at the 130° station in a square section U bend, obtained using an Algebraic Stress Model (left) and a k-ε EddyViscosity Model (right). The ASM results are in better agreement with the experimental data [35].

(a) ReD=17 000

'(b) ReD=40 000Fig.7 Variations of the Nusselt number downstream of an abrupt 2∶1 enlargement in pipe diameter. The superiority of ASM is paramount.
6 Alain Lerat: From Lax-Wendoff to very high order compact schemes
Alain Lerat received his Ph.D. from the University of Paris VI in 1972 under the supervision of R. Peyret. He started his career at Arts et Metiérs ParisTech (then called ENSAM) and became full Professor in 1983. The presentation of his work below is essentially based on [36].

In the eighties, his interest focused on the development of an implicit method of Lax-Wendroff (LW) type allowing to compute steady and unsteady transonic flows without any artificial viscosity. This method was studied and implemented at Onera with J. Sidès and V. Daru [40-42] and also applied to hypersonic flows in the framework of the European Hermes project.
In the nineties, Alain engaged himself and his coworkers at Arts et Metiers ParisTech into a quest for higher efficiency [43-46]. Implicit multi-domain computation of compressible flows were performed with a large number of subdomains without altering the convergence process to a steady-state thanks to original interface treatments. Besides, line-relaxation solution methods previously used in the context of implicit upwind schemes were successfully extended to the implicit LW scheme. This line of work culminated with the design of a characteristic time-stepping scheme, which combined the accuracy of the LW scheme to the robustness of the Roe scheme for calculating multidimensional flows [47]. In this same decade, the general tools developed for hyperbolic systems of conservation laws also allowed the development of an efficient implicit LW scheme for steady and unsteady incompressible one and two-phase flows, taking advantage of the hyperbolic artificial compressibility formulation [48].
Since the start of the new century, Lerat’s work has been mainly devoted to the development of high-order methods for the compressible Euler and Navier-Stokes equations. Together with C. Corre, he designed the Residual-Based Compact (RBC) schemes [49-52]. In such a scheme, the numerical dissipation as well as the consistent part are expressed only in terms of approximations of the complete residualrcontaining all of the terms in the governing equations, including the time derivative. More precisely, the numerical dissipation involves space first derivatives ofrand can be viewed as an extension of the dissipation based on the character-istic time-step matrix previously plugged in the implicit LW scheme. Approximations ofrare compact and deduced from Padè fractions of discrete operators after eliminating the denominators. On a Cartesian mesh, RBC schemes can approximate a hyperbolic system of conservation laws in d-dimension with an order of accuracy of 5 or 7 on a 5d-point stencil. For these odd orders of accuracy, the leading error (of order 5 or 7) is dissipative and dominates the dispersive error (of order 6 or 8), which is a favorable feature for robustness. RBC schemes have been applied to realistic flow configurations in aerodynamics and aero-acoustics and improved in various ways [53-55]. A parallel and related contribution in this period was the analysis and development with F. Falissard and J. Sides of vorticity-preserving schemes (residual-based too) for the compressible Euler equations [56-57]. The latest contribution of Lerat concerns a theoretical study of shock capturing by RBC schemes [58-59]. He found analytical solutions to discrete shock problems of very high-order RBC schemes, which paradoxically cannot be achieved for much simpler schemes such as the first-order Lax-Friedrichs one. Exact shock profiles were also found for the equivalent differential equations of the RBC schemes. These results pave the way for rigorous local corrections of the RBC schemes at discrete shock. Some sample-results obtained by Alain are shown in Figs.8-10: the RBC7 solution of Fig.10 is impressive.

Fig.8 Mach contours around the NACA0012 airfoil M=0.85, α=1°, 256×32 C-mesh, Implicit Lax-Wendroff scheme without artificial viscosity, see [42].

Fig.9 Airfoil-vortex interaction (vorticity snapshots) Vorticity-preserving residual based scheme, see [57].

(a) Exact solution

(b) RBC3 solution
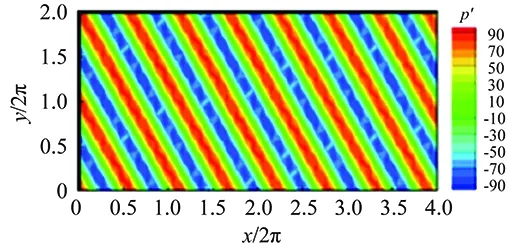
(c) RBC7 solutionFig.10 Instantaneous pressure fluctuation of an oblique wave in a flow at M0=0.4: RBC schemes of 3rdand 7th order on a 40×20 Cartesian grid, compared with the exact solution, see [54].
7 K. W. (Bill) Morton: Finite element and finite volume schemes
Bill Morton started his career at the United Kingdom Atomic Energy Authority, Culham Laboratory, Abingdon, England. In 1976 he came to the attention of mathematicians, physicists and engineers as the co-author of the most authoritative book on numerical methods for initial value problems [60]. In order to pursue his scientific interests, Bill moved first to the Department of Mathematics, University of Reading, Reading, United Kingdom and in 1985 to the Oxford University Computing laboratory, where he worked until his retirement. Morton made several important contributions to numerical methods, in particular, for evolutionary problems, which he describes in his book on the Numerical Solution of Convection-Diffusion Problems [61]. In particular, for the diffusion-convection equation he demon-strated, both by appeal to general theorems and explicitly using discrete Fourier transforms, that the stability results obtained by Fourier analysis for the periodic problem are also highly relevant to the diffusion-convection problem on the unit interval; and that an erroneous stability limit obtained with the matrix method is often hidden by the Gersgorin rescue act [62]. Later, together with J. W. Barret, he determined error bounds for Petrov-Galerkin methods [63] and then considered time-accurate methods for unsteady problems on a fixed mesh: important advantages of the Galerkin formulation are lost as the time step is increased, so he explored first attempts with Petrov-Galerkin and Taylor-Galerkin methods to improve matters. This leads naturally to the study of an important class of methods they called characteristic Galerkin methods. Some of the many possibilities offered by these are described and a particular algorithm is developed and illustrated on a number of test problems in one dimension [64]. Bill’s continuing interest in evolutionary problems is demonstrated by a very important more recent contribution [65]. Here, an in depth analysis is provided for three new evolution Galerkin schemes for a system of hyperbolic equations, and particularly for the wave equation system. The aim is to construct methods which take into account all of the infinitely many directions of propagation of bi-characteristics. The main idea of the evolution Galerkin methods is the following: the initial function is evolved using the characteristic cone and then projected onto a finite element space. A numerical comparison is given of the new methods with already existing methods, both those based on the use of bi-characteristics as well as commonly used finite difference and finite volume methods. The stability properties of the schemes are discussed and error estimates are derived. Another area in which Bill gave important contributions is Finite Volume (FV) methods, in particular using cell vertex discretization. In [66], he used a model problem in one and two dimensions to initiate a theoretical study of such methods, in particular the cell vertex ones, which were already widely used and very successful in solving the Euler and Navier-Stokes equations. In one dimension, FV methods give accurate flux values at volume boundaries, which can be more accurate than for finite element methods. The cell-vertexe schemes are aimed at convection dominated problems and have highly advantageous properties for convection-diffusion problems: but error bounds for these four-point approximations are given only for the pure diffusion problem in one dimension, which indicate their remarkable robustness. Finally, an analysis of the cell vertex scheme for the pure advection problem in two dimensions is given. It explains the insensitivity of the method to mesh stretching in the coordinate directions, maintaining second-order accuracy on any mesh. In [67], together with P. I. Crumpton and J. A. Mackenzie, Bill demonstrated that the inherent advantages of cell-vertex FV schemes obtained for the Euler equations extend to the Navier-Stokes equations in spite of being less compact than cell centred ones. The difficulties in setting up and solving an appropriate set of cell residual equations are overcome by a consistent cell vertex discretization, together with multi-grid pseudo-time stepping procedures which come close to setting the cell residuals to zero; the generalized Lax-Wendroff procedure that is used is a signi-ficant difference from previous attempts to use similar schemes. Results are given for laminar flow, where careful comparisons are made to demonstrate accuracy, and turbulent flow with an algebraic turbulence model. Very impressive results have also been obtained by the cell-vertex method for a standard boundary-layer problem as shown at page 274 of [61]. Such results compare very favorably with those obtained with the Hemker test function and a streamline-diffusion method, of page 213. In the following Figs.11 and 12, some results taken from [67] are shown which demonstrate the quality of the finite-volume cell-vertex solver of the compressible Navier-Stokes equations. Morton’s interest and love for teaching have been demonstrated once more by his last remarkable textbook [68]. Last but not least, attending the many invited or contributed lectures given by Bill at the ICNMFDs, ISCFDs, and ICFDs has always been a great pleasure and a motivating learning experience.

(a) Pressure-coefficient
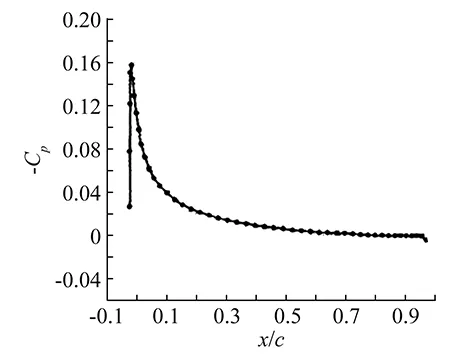
(b) Skin-friction coefficientFig.11 Wall pressure-coefficient and skin-friction coefficient distributions for flow past a NACA0012 airfoil at Re=5 000 and α = 0°.

(a) Pressure-coefficient

(b) Skin-friction coefficientFig.12 Wall-pressure-coefficient and skin-friction distributions for flow past a RAE2822 airfoil at Re=6.5×106 and α=2.79°.
8 Paolo Orlandi: Direct numerical simulations
Paolo Orlandi graduated in 1968 at the University of Rome, in Aerospace Engineering, with a thesis based on the numerical simulation of laminar cavity flows, which was the first research on the numerical solution of the Navier-Stokes equations performed at the Institute of Aerodynamics of that University. During the first years of his academic career, Paolo used his method for computing laminar flows as the starting point for simulating turbulent flows using the Reynolds Averaged Navier-Stokes) equations. In 1983, the Institute of Aerodynamics co-founded the Department of Mechanics and Aeronautics, one of the largest Departments of the College of Engi-neering of the University of Rome, where Orlandi became associate professor in 1982, professor in 1986, and still works. Since the foundation of this Department, important contributions to the world’s CFD were made by its members, in particular, by Paolo and his students, as it will be seen later.
In order to deepen his knowledge of turbulence, his main scientific interest, Paolo spent one sabbatical year (1978) as visiting scholar at Stanford University, where the world famous group of W. C. Reynolds was active, among many other topics, in unsteady boundary layers experiments: professor Reynolds suggested him to make an effort to perform simulations of such flows by one-point turbulence closures, capable of reproducing the complex turbulent kinetic energy budget in the near wall region [69]. Following that work, at the so called Kline Olympics on turbulence (1980-1981), Paolo demonstrated that the one-equation low Reynolds number turbulence model can accurately model a large number of complex turbulent flows.
In 1982, Orlandi started a very fruitful cooperation with Luigi Crocco on spectral closures for isotropic and anisotropic flows. Living in close contact with this old-style scientist, who after retiring was working in his apartment in Rome, deeply affected Paolo’s scientific life. From Luigi, he learned that the driving mechanism for good research is the pleasure to do it without even thinking to its rewards, which will follow. And in fact, with Crocco, Orlandi published his first Journal of Fluid Mechanics paper [70]. In that period Paolo was also using Levi Civita’s tensorial calculus to formulate the Navier-Stokes equations in general curvilinear coordinates, which allowed him to obtain numerical solutions for flows past bodies of complex shape [71]. This research obtained interest at NASA Ames, so that Paolo was invited for several years to spend his summers there and at Stanford University. There, he interacted with scholars and Ph.D. students to develop a numerical method for turbulent flows past complex geometries, that was used by Choi et al.
[72] to perform the first numerical simulation of flows past riblets and explain their mechanism of drag reduction. In that period P. Moin and W.C. Reynolds created the Center for Turbulence Research (CTR) that attracted some of the best scholars from all over the world to its exciting summer school. Orlandi attended such schools regularly until 2002; in that period he performed the first DNS on polymers drag reduction [73] and explained, again by DNS, how such a drag reduction mechanism occurs in rotating pipes [74]. These simulations were performed by means of a new method for solving three-dimensional flows in cylindrical coordinates—developed together with R. Verzicco [75], their most cited paper—which allowed both of them to produce numerous scientific results throughout their entire careers. During the aforementioned summer schools, Orlandi also met some of the most authoritative experts of DNS, such as R. A. Antonia and J. Jimenez; with them Paolo obtained important scientific results, in particular, regarding the wall streaks mechanism generation [76] and the modifications of the flow structures near rough surfaces [77]. During their cooperation, Paolo was invited twice to Madrid and twice to Newcastle. In the year 2000 Orlandi wrote a book [78] that describes his efficient numerical methods for two- and three-dimensional flows, including LES, and has the unique feature of supplying the source Fortran codes, which anyone can use and modify to understand the flow physics using a modern PC. The book had particular success in Asia, and Kluwer was glad to enter that market.
Later, Orlandi became interested, and still is, in geophysical flows, interacting with E. J. Hopfinger in Grenoble, G. J. F. van Heijst in Eindhoven and G. F. Carnevale in S.Diego; with them he wrote papers on JFM, Physics of Fluids, and Experiments in Fluids. Paolo’s interaction with prominent scholars was also favoured by the Ph.D. students of the University of Rome he supervised. All of these had important scientific cooperations around the world—with and without Paolo. Here only a few are mentioned: M. Briscolini, P. Cavazza, M. Fatica (who had research and teaching positions for several years at CTR), S. Leonardi (who is professor at the University of Texas at Dallas), M. Mammetti, F. Tessicini (who, after working at the Imperial College in London performing LES of complex aeronautical flows, in 2008 was hired as aerodynamicist at the Renault branch of racing cars) and R. Verzicco (a world reknown professor of Fluid Dynamics at the Poyitechnic of Bari first and now at the University of Rome “Tor Vergata”). In particular, Leonardi during his thesis was holding the link with prof. Antonia in Newcastle: the two groups could perform for the first time DNSs of flows past rough walls, contributing to increase and clarify the comprehension of the complex physics near rough surfaces; and Orlandi’s group created one of the most valuable database of rough turbulent flows. In the last years, Paolo started a very productive interaction with S. Pirozzoli (the first scholar of Orlandi’s school invited to contribute to the Annual Review of Fluid mechanics [79]) and M. Bernardini, by using efficient codes based on second-order-accurate energy-conserving methods and MPIs: they were able to contribute to prove that the Euler equations lead to a finite time singularity starting with smooth initial conditions and that the Navier-Stokes equations do not [80]; also, they were able to obtain the DNS of turbulent channel flow atReτ=4000 [81], the highest value achieved so far. Last but not least, Orlandi was invited to write two review articles for the Applied Mechanics review [82, 83]. In the following Figs.13-15, some of the results presented in [75] are shown to demonstrate the quality of the numerical method proposed there.

(a) 257×513 grid

(b) 129×129 gridFig.13 Azimuthal vorticity field for a vortex ring impinging on a wall at Re=2 895 and t=30. Tick marks at the axis are every x, r=r0.
9 Olivier Pironneau: Finite element methods and optimum design
Olivier Pironneau did his Ph.D. at UC-Berkeley in optimization and control. So when he moved to Cambridge, UK, as a postdoc of Sir James Lighthill, he brought with him calculus of variations and the conjugate gradient method. In search of an application, he found and solved the optimal shape problem for Stokes flow in 1973 [84]. The numerical solution was obtained by performing by hand one iteration of the method of steepest descent. The technique was extended to the Navie-Stokes equations and arouse the interest of airplane industries. A first attempt to build a numerical method based on potential flow and boundary layer theory failed. At the same time the Dassault aviation company began to work on the finite element method for fluids. A team of five, which included R. Glowinski and J. Periaux, managed to optimize an airfoil—using adjoints and conjugate gradients as documented in [85]—and also to calculate the flow around a complete aircraft in 1982. The team was ready to optimize the full airplane but had to wait ten more years to obtain a suitable computer. Thanks to the talent of B. Mohammadi, this was done at the end of the nineties in cooperation with Dassault. At about the same time A. Jameson embarked in a similar program by a similar method but with finite volume schemes. For such large optimisation problems, it is important to compute the exact gradients of the discretized problem rather than discretize the continuous gradients. The methodology was laid in 1978 for an electromagnetic problem with Maxwell equations and the optimization of a rotor/stator motor by the finite element method [86]. All of these results are explained in the book [85]. To extend the technology to complex turbulent flows, a formal differentiation of the equations was used so as to obtain the adjoint states by using Automatic Differentiation (Tapenade in reverse mode). This motivated a second book with B. Mohammadi [87].

(a) Azimuthal vorticity (cylindrical coordinates)

(b) ωx (Cartesian coordinates)

(c) ωz(Cartesian coordinates)Fig.14 Vorticity contour plots for a vortex ring impinging on a wall at Re=1 389 and t=48. Tick marks at every r0. In these simulations the axial extension of the computational domain was 4r0.
(a) (257×513 grid) ω-ψ formulation of [79]

(b)Fig.15 Time evolution of the peak vorticities, normalized to the peak vorticity of the ring at t=0, for the vortex ring impinging on a wall at Re=2895.
Pironneau’s most recent contribution to the field of shape optimization for fluids established that, when the flow has shocks, the discrete gradients converge to the continuous ones weakly, because of Dirac masses [88].
10 Luigi Quartapelle: Integral conditions for the vorticity and the pressure in incom-pressible viscous flows
Luigi Quartapelle graduated in nuclear Engineering at the Polytechnic of Milan in 1971. He started his career as a physics lecturer and professor at that university and then he moved to teach Fluid dynamics, which has been his main research interest since 1980. He has given important contributions in several areas of CFD,inprimisFEMs and projection methods, see [89,90] and the references therein; but in the author’s opinion, Quartapelle will be remembered for years to come for his integral conditions for the vorticity [91] and the pressure [92] in incompressible viscous flows. He has also written a book on the numerical solution of the incom-pressible Navier-Stokes equations [93] which describes his numerous contributions in the field. In the following, the abstract of [91] is reported, which describes with the utmost clarity what integral conditions are about: “The problem of evaluating the boundary values of the vorticity in the calculation of two-dimensional viscous flows is considered. It is shown that the splitting of the fourth-order equation for the stream function into two second-order problems implies specific integral conditions which fix the abstract projection of the vorticity field with respect to the linear manifold of the harmonic functions. These conditions are a direct consequence of the boundary conditions on the velocity, and ensure satisfaction of physically essential con-servation laws for the vorticity. The discrete analogue of the projection conditions produces as many algebraic equations as the number of boundary points and requires the solution of an equal number of Dirichlet problems. In the particular case of the linear Stokes equations, a direct, i.e., non-iterative, method of solutions is obtained. Steady and unsteady computational schemes relying on the projection conditions on the vorticity are introduced and extensive numerical results of the driven-cavity model problem are reported and discussed”. It is noteworthy that, although the integral conditions can be replaced by a local implementation of the Neumann condition for the stream function at solid boundaries, in addition to their intrinsic scientific value, they can serve as a guiding light for a critical review of the vorticity conditions in the numerical solution of the vorticity-stream function equations [94]. Concerning pressure conditions, the abstract of [92] is reported: “The problem of finding the correct conditions for the pressure in the time discretized Navier-Stokes equations when the incompressibility constraint is replaced by a Poisson equation for the pressure is critically examined. It is shown that the pressure conditions required in a nonfractional-step scheme to formulate the problem as a split second-order equations are of an integral character and similar to the previously discovered integral conditions for the vorticity. The novel integral conditions for the pressure are used to derive a finite element method which is very similar to that developed by Glowinski and Pironneau [C. R. Acad.Sci. Paris Sér. A 282(1976)] and is the finite element counterpart of the influence matrix method of Kleiser and Shumann [Notes on Numerical Fluid Mechanics, 2, Vieweg, 1980]”. More recently, Quartapelle has published several papers on spectral methods, see, e. g., [95, 96] and the references therein. Among his many students, the author likes to mention S. Rebay [97] and F. Auteri, with whom Luigi wrote several journal papers and two outstanding Fluid Dynamics textbooks [98, 99]. Here, it is the author’s pleasure to present some results obtained by Luigi at the Fifth IAHR meeting held in Rome on May 24-25 1982 [100]. There, several scientists tested their methods versus a somewhat challenging test case proposed by P. Roache [101], namely, flow past a channel whose length (xout) is scaled with the Reynolds number (Re), for which, asReincreases the vorticity at the wall vsx/xoutbecomes independent ofRe, leading to a self-similar flow, see [100, 101] for details (Fig.16). A parabolic velocity profile is assumed as the boundary condition at the entrance of the channel, so that a singularity arises at the left corner of the channel’s bottom, which is not perfectly horizontal. Such a singularity becomes negligible asReincreases so that the most difficult solution is obtained for the lowestReconsidered, namely,Re= 10, where difficulties may arise for the aforementioned singularity for the vorticity, see the Fig.17. It turned out that Quartapelle’s vorticity-stream function finite element solution was the most accurate one, as compared with a finer mesh benchmark solution provided by Cliffe et al. [AERE-R1068], and the velocity-pressure finite element solution provided by Luigi was chosen as the benchmark for evaluating all other ones, see [100], for details.

Fig.16 Wall vorticity profiles versus x/xout, obtained by all participants using the prescribed 21×21 grid.
11 Philip L. Roe: Approximate Riemann solvers, parameter vectors and difference schemes
Phil Roe obtained a Bachelor’s degree in Engineering from Cambridge University before starting his career as a research scientist at the Royal Aircraft Establishment, Bedford, United Kingdom, in 1962, where he worked initially in the field of hypersonic wave-rider aerodynamics. He later shifted to CFD and devised the Roe solver for the numerical computation of compressible flows with shocks. His famous paper, now cited more than 7000 times (Google scholar), “Approximate Riemann solvers, parameter vectors, and difference schemes”[7], was reprinted with an appreciation by M. J. Baines in a special issue of the journal devoted to its most influential articles [102]. The illustration included in the chapter on S. K. Godunov demonstrates that there is little difference between the exact and approximate solvers when used as flux functions. In 1981, he began a fruitful collaboration with K. W. Morton, M. J. Baines and P. K. Sweby at the University of Reading, resulting in papers presented to the GAMM conferences. These papers, for example [103], introduced limiter diagrams for theminmodandSuperbeelimiters that are now part of standard practice.
In 1984 he began the academic phase of his career, moving to Cranfield Institute of Technology, England. In 1986 he was invited to write a review article [104] onCharacteristic-basedSchemesfortheEulerequationsforVolume 1 of Annual Review of Fluid Mechanics. Since 1990, he is full professor at the Department of Aerospace Engineering of the University of Michigan at Ann Arbor, Michigan. Roe is Fellow of the AIAA and obtained the following Honors and Awards: NASA Group Achievement Award (1992); Department of Aerospace Engineering Research Award (1994, 2000-2001). In 2013 a two-day Symposium was organized preceding the AIAA Conference in San Diego to honor him jointly with B. van Leer and A. Jameson.
After moving to Cranfield in 1984, Phil began a long quest, still not completely fulfilled, for truly multidimensional concepts of upwinding, beginning in 1987 with a short informal note introducing what came to be known as residual distribution schemes. This led to a lasting collaboration with H. Deconinck at the von Karman Institute in Brussels, which continued after Roe’s move to Ann Arbor in 1990 and involved several students on both sides of the Atlantic [105]. These schemes have many interesting features and are the subject of current research in several countries.
12 Bram van Leer: Towards the ultimate Riemann solver
Bram van Leer was a doctoral student in astrophysics at Leiden Observatory (1966-70) when he got interested in CFD for the sake of solving cosmic flow problems. His first major result in CFD was the formulation of the upwind numerical flux function for a hyperbolic system of conservation laws [106]:
Fup=(Fj+Fj+1)/2-|A|j+1/2(uj+1-uj)
Here,thematrixAappears for the first time, defined as the matrix that has the same eigenvectors as the flux Jacobian, but the corresponding eigenvalues are the moduli of those ofA. The subscriptj+1/2 indicates a representative or average value on the intervalxj-xj+1. It was no less than 10 years later that Phil Roe [107] first presented his much used averaging formulas. Next, Van Leer succeeded in circumventing Godunov’s barrier theorem, by limiting the second-order term in the Lax-Wendroff scheme, as a function of the non-smoothness of the numerical solution itself. This is a nonlinear technique even for a linear equation. Having discovered this basic principle, he planned a series of three articles titledTowardstheultimateconservativedifferencescheme[108-110], which advanced from scalar non-conservative but non-oscillatory (part I) via scalar conservative non-oscillatory (part II) to conservative non-oscillatory Euler (part III). The finite-difference schemes for the Euler Equations turned out to be unattractive because of their many terms; a switch to the finite-volume formulation completely cleared this up and led to Part IV (finite-volume scalar) [111] and, finally, Part V (finite-volume Lagrange and Euler) titledASecond-OrderSequeltoGodunov’sMethod[112], now cited more than 4 000 times (Google Scholar). The series contains several original techniques that have found their way into the CFD community. In Part II, two limiters are presented, later called by van Leerdoubleminmod(after Osher’sminmodlimiter) and its smoothed versionharmonic; the latter is sometimes referred to in the literature asVanLeer’slimiter. Part IV,Anewapproachtonumericalconvection, describes a group of 6 second- and third-order schemes that includes two Discontinuous Galerkin schemes with exact time-integration. Bram was not the only one to circumvent Godunov’s barrier theorem using nonlinear limiting; similar techniques were developed independently around the same time by Boris [113] and by V. P. Kolgan, a Russian researcher unknown in the West. In 2011, van Leer devoted an article to Kolgan’s contributions [114] and had Kolgan’s 1972 report reprinted in trans-lation [115].
After the publication of the series (1972-1979) Bram spent two years at ICASE (NASA LaRC), where he was engaged by NASA engineers interested in his numerical expertise. This led to van Leer’s differentiable flux-vector splitting [116] and the development of the block-structured codes CFL2D and CFL3D [117-118], which still are heavily used. Other seminal papers from these years are the review of upwind methods with Harten and Lax [119], the AMS summer seminar paper [120] detailing the differences and resemblances between upwind fluxes and Jameson’s flux formula, and that on upwind relaxation methods [121]; the latter includes the concept ofSwitchedEvolution-Relaxationfor automatically choosing the time-step in an implicit marching scheme, which was inspired by a seminar by Napolitano at ICASE in 1982. Last but not least, with Roe and Leveque he produced a paper in 1983 composed entirely of limericks,Aone-sidedview. Printed first as an ICASE unofficial report, it was finally published in the conference book in honor of Roe’s 60th birthday, with an introduction by van Leer about its genesis [122].
In 1986 Bram became a full professor of Aerospace Engineering at the University of Michigan; from 2007 he held an endowed chair, till his retirement in 2012. Among his awards, are an honorary doctorate from the Free University of Brussels, two NASA LaRC group awards, and the AIAA 2010 Fluid Dynamics Award for a lifetime of dedication to (C)FD research and education.
The author had the privilege—as organizer and chairman of the 13thICNMF, Rome, 1992—of choosing van Leer as the first invited lecturer. There, Bram gave an inspiring talk about multi-dimensional upwind methods [123].
Finally, a numerical solution taken from [112] is shown to demonstrate the superiority of a second order solution with respect to the first-order one shown at the beginning of this paper (Fig.18).

(a) p~x

(b) u~xFig.18 Exact solutions and cell averages (circles) of ρ and u, obtained with MUSCL for Sod’s problem. Initial values: u = 0; ρ=p=1 for x<0.5; ρ=0.125, p = 1, for x>0.5; γ=1.4; CFL=0.9; solution after 34 time steps at t=0.14154.
13 Michele Napolitano: High Reynolds number separated flows (Last and Least)
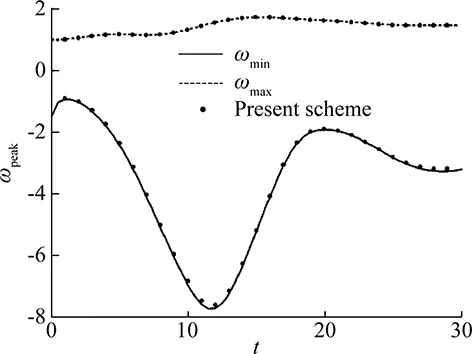
Michele Napolitano started his career at the Polytechnic of Turin, where he graduated in Mechanical Engineering with a thesis on unsteady flows through screens [124] and soon after moved to Bari, where he became professor in 1980. In the seventies, as an assistant professor on leave, he obtained a MSc and a Ph. D. under M. J. Werle and R. T. Davis at the University of Cincinnati. He developed Alternating Direction Implicit (ADI) methods for solving the Navier-Stokes equations and the triple-deck equations for high Reynolds number weakly separated flows [125-128]. His main contributions were to devise ADI methods that could account for upstream propagations in separated flows for the supersonic as well as subsonic triple-deck equations. For the latter equation, the pressure is related to the displacement thickness by a Cauchy integral, that becomes a linear system upon discretization, whose matrix is inverted once and for all, so that the pressure solution at every time step is obtained by a very fast matrix-vector multiplication. Later, when spending his summers at ICASE (NASA LaRC), he was exposed to the work of B. van Leer on upwind methods, that guarantee the diagonal dominance of the linearized systems to be solved at each iteration of the solution procedure. He immediately understood that the line Gauss-Seidel method was the most effective solver for high Reynolds number weakly separated flows, if combined with the delta form of the equations: the left-hand sides advection operators are discretized by a first-order-accurate upwind scheme and the right hand side residual are discretized by second-order accurate-central differen-ces or even high order splines [129]. In this way, the linear systems to be solved at each pseudo-time step are diagonally dominant and the steady solution is numerical viscosity-free. This idea has been applied in [130] to both the incompressible and compressible Navier-Stokes equations and has been later made famous by R. W. MacCormack and G. V. Chandler [131]. Last but not least, in order to alleviate the slow convergence at very high Reynolds numbers, due to the use of a deferred correction approach, Napolitano has equipped his solver with a simple though effective multi-grid approach [132]. In particular, he realized that a fully implicit approach using the finest grid is needed in the direction normal to the wall, whereas semi-coarsening in the stream-wise direction is a very effective means for upstream propagation [133, 134]. The accuracy and efficiency of the scheme developed by Napolitano allowed him and his coworkers to obtain benchmark solutions for high Re weakly separated external flows [133-135]. Figs.19-21, taken from [133], show the geometry and the grid of Inoue’s problem—a boundary layer flow past a diffuser, the convergence of the method using from 1 to 4 grids, and the wall vorticity values obtained with increasingly refined grids, respectively. One work unit is the CPU time required by a single iteration on the finest grid. Figures 22 and 23(a, b), taken from [134], show the geometry and the boundary conditions for the flow past a backward facing step and the vorticity profiles at the upper and lower walls, obtained using increasingly refined grids. Finally, the table 1 shows the benchmark values (obtained by Richardson’s extrapolation after removing the influence of the downstream boundary condition location, see [134], for details) for the abscissas of the primary reattachment point (on the lower wall) and of the secondary separation and reattachment points (on the upper wall). For the problem as described in Fig.22 (a parabolic velocity profile is assumed immediately ahead of the step), these values are correct to all digits. Similar benchmark solutions are provided for sudden symmetric expansions in a 2D channel and in a circular duct [135].

Fig.19 Geometry and grid for Inoue’s diffuser flow (IDF).
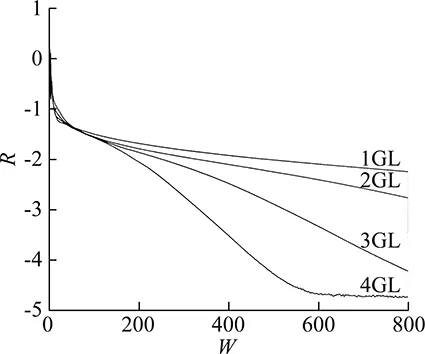
Fig.20 Convergence histories for IDF, using from 1 to 4 Grid Levels.

Fig.21 Wall vorticity distribution for IDF.

Fig.22 Backward Facing Step (BFS) geometry and boundary conditions.

Re200400600800X1R/h5.348.6310.7212.16X2S/h-7.968.719.67X2R/h-10.4416.2320.96
This chapter would be incomplete without mentioning some of the work on implicit methods for the lambda formulation, see [136] and the references therein, which led M. Napolitano to give an invited lecture to the 10th ICNMFD-Beijing [137] and to become a member of the Scientific Committee of such a conference, as well as some of the major contributions of the younger colleagues of M. Napolitano at the Politecnico di Bari, who have all been his students and have overcome their mentor—the major merit of a scholar is to choose and motivate his co-workers. The major contributions have been in developing and applying: i) methods for solving the vorticity velocity Navier-Stokes equations, capable of satisfying the solenoidality constraint and the vorticity definition, exactly in the discrete [138-140]; ii) low- and high-order fluctuation splitting schemes using triangles as well as quadrilaterals see, e. g., [141-144] and the references therein; iii) the first Immersed Boundary Method [IBM] for the compressible Euler and Navier-Stokes equations[145]; iv) numerical methods for biomechanical applications, transition and com-bustion [146-148]. Last but not least, on the occasion of his 60th birthday, Computers & Fluids has dedicated him a special issue in recognition of his contributions to CFD.
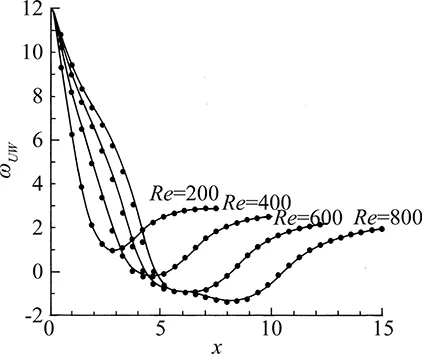
(a) Upper wall vorticity distributions

(b) Lower wall vorticity distributionsFig.23 Upper and lower wall vorticity distributions for flows past a BFS.
Acknowledgements: This work has been funded by MIUR (PRIN 2010-11, and Cofinlab 2001). The author is grateful to M. Germano, R. Glowinski, A. Lerat, K. W. Morton, P. Orlandi, O. Pironneau, P. L. Roe and B. van Leer, for kindly providing either their contributions—that the author has somewhat modified—or some useful information. The other colleagues will have to forgive him for any inaccuracy. The author also thanks the Organizing Committee of ICCFD8 for inviting him to write this paper, being well aware that each of the scientists discussed here—as well as many others not considered in this paper—would have been more deserving than him. Last, but not least, he is grateful to all of his coauthors throughout his academic career.
[1]Godunov S K. A finite-difference method for the numerical computation and discontinuous solutions of the equations of fluid dynamics[J]. Mat. Sb. , 1959,47:271-290.
[2]Godunov S K. Reminiscences about difference schemes[J]. Journal of Computational Physics, 1999, 153 (1):6-25.
[3]Godunov S K. Thermodynamically consistent systems of hyperbolic equation[C]//Computational Fluid Dynamics 2010, A. Kuzmin Ed., Springer-Verlag, 2011: 31-33 (Proceedings of the ICCFD6).
[4]Godunov S K. Computation of discontinuous solutions of fluid dynamics equations with entropy nondecrease guarantee[J]. Computational Mathematics and Mathematical Physics, 2014, 54 (6): 1012-1024.
[5]Van Leer B. An Introduction to the article “Reminiscences about difference schemes” by S. K. Godunov[J]. Journal of Computational Physics, 1999, 153 (1):1-5.
[6]Hirsch C. Numerical computation of internal and external flows. Volume 2:Computational methods for inviscid and viscous flows[M]. John Wiley and Sons, 1990.
[7]Roe P L. Approximate Riemann solvers, parameter vectors, and difference scheme[J]. Journal of Computational Physics, 1981, 43 (2): 357-372.
[8]Germano M. A proposal for a redefinition of the turbulent stresses in the filtered Navier-Stokes equations[J]. Physics of Fluids, 1986, 29: 2323-2324.
[9]Germano M. Averaging invariance of the turbulent equations and similar subgrid modelling[M]. Stanford, CA: CTR Manuscript 116, 1990.
[10]Germano M. Turbulence: the filtering approach[J]. Journal of Fluid Mechanics, 1992, 238: 325-336.
[11]Germano M. Fundamentals of large eddy simulation[M]//Peyret R, Krause E. Advanced turbulent flows computations. CISM Courses and Lectures 395, Springer, 2000: 81-130.
[12]Germano M, Piomelli U, Moin P, et al. A dynamic subgrid-scale eddy viscosity model[J]. Physics of Fluids A, 1991, 3: 1760-1765.
[13]Glowinski R. Viscous flow simulations by finite element methods and related numerical techniques[M]//Murman E M, Abarbanel S S. Progress in supercomputing in Computational Fluid Dynamics. Birkhäuser, Boston: 1985,173-210.
[14]Bristeau M O, Glowinski R, Périaux J, et al. On the numerical solution of nonlinear problems in fluid dynamics by least squares and finite element methods (II). Application to transonic flow simulations[J]. Computer Methods in Applied Mechanics and Engineering, 1985, 51:363-394.
[15]Glowinski R. Numerical methods for nonlinear variational problems[M]. New-York, NY: Springer, 1984 (2nd Printing: 2008).
[16]Bristeau M O, Glowinski R, Périaux J. Numerical methods for the Navier-Stokes equations. Applications to the simulation of compressible and incompressible viscous flows[J]. Computer Physics Reports, 1987, 6 (1): 73-187.
[17]Glowinski R. Finite element methods for incompressible viscous flow[M]// Ciarlet P G, Lions J L. Handbook of numerical analysis. North-Holland, Amsterdam, 2003, 9: 3-1176.
[18]Dean E J, Glowinski R, Guidoboni G. On the numerical simulation of Bingham visco-plastic flow: old and new results[J]. Journal of Non-Newtonian Fluid Mechanics, 2007, 142 (1): 36-62.
[19]Glowinski R, Pan T W, Hesla T I, et al. A distributed Lagrange multiplier/fictitious domain method for flows around moving rigid bodies: Application to particulate flows[J]. International Journal of Multiphase Flow, 1999, 25: 755-794.
[20]Glowinski R, Pan T W, Hesla T I, et al. A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow[J]. Journal of Computational Physics, 2001, 169: 363-426.
[21]Glowinski R, Pan T W, Hesla T I, et al. A distributed Lagrange multiplier/fictitious domain method for flows around moving rigid bodies: application to particulate flow[J]. International Journal for Numerical Methods in Fluids, 1999, 30 (8): 1043-1066.
[22]Pan T W, Joseph D D, Glowinski R. Modelling Rayleigh-Taylor instability of a sedimenting suspension of several thousand circular particles in a direct numerical simulation[J]. Journal of Fluid Mechanics, 2001, 434: 23-37.
[23]Pan T W, Joseph D D, Bai R, et al. Fluidization of 1204 spheres: Simulation and experiment[J]. Journal of Fluid Mechanics, 2002, 451: 169-191.
[24]Pan T W, Glowinski R, Hou S. Direct numerical simulation of pattern formation in a rotating suspension of non-Brownian settling particles in a fully filled cylinder[J]. Computers and Structures, 2007, 85: 955-969.
[25]Hirsch C. Numerical computation of internal and external flows. Volume 1: Fundamentals of numerical discretization[M]. John Wiley and Sons, 1988.
[26]Kang S, Hirsch C. Numerical simulation of three-dimensional viscous flow in a linear compressor cascade with tip clearance[J]. Journal of Turbomachinery, 1996, 118 (3): 492-502.
[27]Coutier-Delgosha O, Fortes-Patella R, Reboud J -L, et al. Numerical simulation of cavitating flow in 2D and 3D inducer geometries[J]. International Journal for Numerical Methods in Fluids, 2005, 48 (2) : 135-167.
[28]Van Ertbruggen C, Hirsch C, Paiva M. Anatomically based three-dimensional model of airways to simulate flow and particle transport using computational fluid dynamics[J]. Journal of Applied Physiology, 2005, 98 (3): 970-980.
[29]Oberkampf W L, Trucano T G, Hirsch C. Verification, validation, and predictive capability in computational engineering and physics[J]. Applied Mechanics Reviews, 2004, 57 (1-6) :345-384.
[30]Launder B E, Spalding D B. The numerical computation of turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 1974, 3 (2) :269-289.
[31]Launder B E, Spalding D B. Lectures in mathematical models in turbulence[M]. Academic Press, 1972.
[32]Launder B E, Sharma B I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc[J]. Letters in Heat and Mass Transfer, 1974, 1 (2): 131-137.
[33]Gibson M M, Launder B E. Ground effects on pressure fluctuations in the atmospheric boundary layer[J]. Journal of Fluid Mechanics, 1978, 86 (3): 491-511.
[34]Launder B E, Reece G J, Rodi W. Progress in the development of a Reynolds-stress turbulence closure[J]. Journal of Fluid Mechanics, 1975, 68 (3): 537-566.
[35]Launder B E. Second moment closure and its use in modelling turbulent industrial flow[J]. International Journal of Numerical methods in Fluids, 1989, 9 (8): 963-985.
[36]Corre C, Hafez M. Preface to the special issue dedicated to Prof. A. Lerat on the occasion of his 60thbirthday[J]. Computers & Fluids, 2009, 38: 113.
[37]Lerat A, Peyret R. Noncentered schemes and shock propagation problems[J]. Computers & Fluids, 1974, 2: 35-52.
[38]Lerat A, Peyret R. The problem of spurious oscillations in the numerical solution of the equations of gas dynamics[J]. Lecture Notes in Physics, 1975, 35: 251-256.
[39]Lerat A. Numerical shock structure and nonlinear corrections for differences schemes in conservation form[J]. Lecture Notes in Physics, 1979, 90: 345-351.
[40]Lerat A, Sides J, Daru V. An implicit finite-volume method for solving the Euler equations[J]. Lecture Notes in Physics, 1982, 170: 343-349.
[41]Lerat A. Implicit methods of second-order accuracy for the Euler equations[J]. AIAA Journal, 1985, 23: 33-40.
[42]Lerat A, Sides J. Efficient solution of the steady Euler equations with a centered implicit method[M]//Numerical methods for fluid dynamics IV. Clarendon Press, 1988: 65-86.
[43]Khalfallah K, Lacombe G, Lerat A. Analysis of implicit treatments for a centred Euler solver[J]. Computers & Fluids, 1993, 22: 381-406.
[44]Lerat A. Multidimensional centered schemes of the Lax-Wendroff type[J]. Computational Fluid Dynamics Review, J. Wiley, 1995: 124-140.
[45]Lerat A, Wu Z. Stable conservative multidomain treatments for implicit Euler solvers[J]. Journal of Computational Physics, 1996, 123: 45-64.
[46]Corre C, Khalfallah K, Lerat A. Line-relaxation methods for a class of centred schemes[J]. Computational Fluid Dynamics Journal, 1996, 5: 213-246.
[47]Huang H, Lerat A. Second-order upwinding through a characteristic time-step matrix for compressible flow calculations[J]. Journal of Computational Physics, 1998, 142: 445-472.
[48]Granier B, Lerat A, Wu Z. An implicit centered scheme for steady and unsteady incompressible one and two-phase flows[J]. Computers & Fluids, 1997, 26: 373-393.
[49]Lerat A, Corre C. A residual-based compact scheme for the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 2001, 170: 642-675.
[50]Lerat A, Corre C. Residual-based compact schemes for multidimensional hyperbolic systems of conservation laws[J]. Computers & Fluids, 2002, 31: 639-661.
[51]Lerat A, Corre C. Higher order residual-based compact schemes on structured grids[M]//CFD-higher order discretization methods. VKI-LS 2006-01, 2006: 1-111.
[52]Corre C, Falissard F, Lerat A. High order residual-based compact schemes for compressible inviscid flows[J]. Computers & Fluids, 2007, 36:1567-1582.
[53]Corre C, Lerat A. A residual-based compact scheme of optimal order for hyperbolic problems[J]. Computers & Fluids, 2011, 41: 94-102.
[54]Lerat A, Cinnella P, Michel B, Falissard F. High-order residual-based compact schemes for aerodynamics and aeroacoustics[J]. Computers & Fluids, 2012, 61: 31-38.
[55]Lerat A, Grimich K, Cinnella P. On the design of high order residual-based dissipation for unsteady compressible flows[J]. Journal of Computational Physics, 2013, 235: 32-51.
[56]Lerat A, Falissard F, Sides J. Vorticity-preserving schemes for the compressible Euler equations[J]. Journal of Computational Physics, 2007, 225: 635-651.
[57]Falissard F, Lerat A, Sides J. Computation of airfoil-vortex interaction using a vorticity-preserving scheme[J]. AIAA Journal, 2008, 46: 1614-1623.
[58]Lerat A. Steady discrete shocks of high-order RBC schemes[J]. Journal of Computational Physics, 2013, 252: 350-364.
[59]Lerat A. Steady discrete shocks of 5thand 7th-order RBC schemes and shock profiles of their equivalent differential equations[J]. Journal of Computational Physics, 2014, 272: 629-643.
[60]Richtmeyer R D, Morton K W. Difference methods for initial-value problems[M]. Second edition. Interscience Publishers, a division of John Wiley and Sons, 1967.
[61]Morton K W. Numerical solution of convection-diffusion problems[M]. Applied Mathematics and Mathematics Computation 12. London: Chapman & Hall, 1996.
[62]Morton K W. Stability of finite difference approximations to a diffusion-convection equation[J]. International Journal for Numerical methods in Engineering, 1980, 15 (5): 677-683.
[63]Barret J W, Morton K W. Approximate symmetrization and Petrov-Galerkin methods for diffusion-convection problems[J]. Computer Methods in Applied Mechanics and Engineering, 1984, 45 (1-3): 97-122.
[64]Morton K W. Generalised Galerkin methods for hyperbolic problems[J]. Computer Methods in Applied Mechanics and Engineering, 1984, 45 (1-3): 97-122.
[66]Morton K W, Suli E. Finite volume methods and their analysis[J]. IMA Journal of Numerical Analysis, 1991, 11 (2): 241-260.
[67]Crumpton P I, Mackenzie J A, Morton K W. Cell vertex algorithms for the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 1993, 109 (1) : 1-15.
[68]Morton K W, Mayers D F. Numerical solution of partial differential equations: an introduction.[M]. II Edition. Cambridge University press, 2005.
[69]Orlandi P, Ferziger J H. Implicit noniterative schemes for unsteady boundary layers[J]. AIAA Journal, 1981,19 (11):1408-1414.
[70]Crocco L, Orlandi P. A transformation for the energy-transfer term in isotropic turbulence[J]. Journal of Fluid Mechanics, 1985, 161: 405-424.
[71]Orlandi P, Cunsolo D. Two-dimensional laminar flow in elbows[J]. ASME Transactions, Journal of Fluids Engineering, 1979, 101: 276-283.
[72]Choi H, Moin P, Kim J. Direct simulation of turbulent flow over riblets[J]. Journal of Fluid Mechanics, 1993, 255: 503-539.
[73]Orlandi P. A tentative approach to the direct simulation of drag reduction by polymers[J]. Journal of non-Newtonian fluid mechanics, 1995, 60 (2): 277-301.
[74]Orlandi P, Fatica M. Direct simulations of turbulent flow in a pipe rotating about its axis[J]. Journal of Fluid Mechanics, 343: 43-72.
[75]Verzicco R, Orlandi P. A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates[J]. Journal of Computational Physics, 1996,123 (2): 402-414.
[76]Orlandi P, Jimenez J. On the generation of turbulent wall friction[J]. Physics of Fluids, 1994,6 (2): 634-641.
[77]Leonardi S, Orlandi P, Smalley R J, Djenidi L, Antonia R A. Direct numerical simulations of turbulent channel flow with transverse square bars on one wall[J]. Journal of Fluid Mechanics, 2003, 491: 229-238.
[78]Orlandi P. Fluid flow phenomena: a numerical toolkit[M]. The Nederlands: Kluwer Academic Publishers.(P.O. Box 17, 3300 AA Dordrecht) 2000 (Reprinted 2001).
[79]Pirozzoli S. Numerical methods for high-speed flows[J]. Annual Review of Fluid Mechanics, 2011, 43: 163-194.
[80]Orlandi P, Pirozzoli S, Carnevale G F. Vortex events in Euler and Navier-Stokes simulations with smooth initial conditions[J]. Journal of Fluid Mechanics, 2012, 690: 288-320.
[81]Bernardini M, Pirozzoli S, Orlandi P. Velocity statistics in turbulent channel flow up toReτ=4000[J]. Journal of Fluid Mechanics, 2014 ,742: 171-191.
[82]Verzicco R, Orlandi P. Wall/vortex-ring interactions[J]. Applied Mechanics Review, 1996, 49 (10 PART 1): 447-460.
[83]Antonia R A, Orlandi P. Effect of Schmidt number on small-scale passive scalar turbulence[J]. Applied Mechanics Review. 2003, 56 (6): 615-632.
[84]Pironneau O. Optimum shape design in Stokes flow[J]. Journal of Fluid Mechanics, 1973, 59 (1).
[85]Pironneau O. Optimal shape design of elliptic systems[M]. New York: Springer-Verlag, 1984.
[86]Marrocco A, Pironneau O. Optimum design with Lagrangian finite elements; design of an electromagnet[J]. Computer Methods in Applied Mechanics and Engineering, 1978, 15 (3) : 273-288.
[87]Mohammadi B, Pironneau O. Applied optimal shape design[M]. 2ndEd. Oxford University Press , 2009.
[88]Alauzet F, Pironneau O. Continuous and discrete adjoints to the Euler equations for fluids[J]. International Journal for Numerical Methods in Fluids, 2012, 70 (2): 135-157.
[89]Donea J, Giuliani S, Laval H, et al. Finite element solution of the unsteady Navier-Stokes equations by a fractional step method [J]. Computer Methods in Applied Mechanics and Engineering 1982, 30 (1): 53-73.
[90]Guermond J -L, Quartapelle L. Calculation of incompressible viscous flows by an unconditional-ly stable projection FEM[J]. Journal of Computational Physics, 1997, 132 (1): 12-33.
[91]Quartapelle L. Vorticity conditioning in the computation of two-dimensional viscous flows[J]. Journal of Computational Physics, 1981, 40 (2): 453-477.
[92]Quartapelle L, Napolitano M. Integral conditions for the pressure in the computation of incompressible viscous flows[J]. Journal of Computational Physics, 1986, 62 (2): 340-348.
[93]Quartapelle L. Numerical Solutions of the incompressible Navier-Stokes Equations[M]. ISNM, Birkhauser Verlag, Basel, 1993, 3.
[94]Napolitano M, Pascazio G, Quartapelle L. A review of vorticity conditions in the numerical solution of the-equations[J]. Computers & Fluids, 1999, 28 (2) :139-185.
[95]Auteri F, Quartapelle L. Spectral solvers for spherical elliptic problems[J]. Journal of Computational Physics, 2007, 227 (1): 36-54.
[96]Auteri F, Quartapelle L. Galerkin-Laguerre spectral solution of self-similar boundary layer problems[J]. Communications in Computational Physics, 2012, 12 (5): 1329-1358.
[97]Quartapelle L, Reba Y S. Numerical solutions of two-point boundary value problems[J]. Journal of Computational Physics, 1990, 86 (2): 314-354.
[98]Quartapelle L, Auteri F. Fluidodinamica incomprimibile[M]. Casa Editrice Ambrosiana, Rozzano (MI), 2013.
[99]Quartapelle L, Auteri F. Fluidodinamica comprimibile[M]. Casa Editrice Ambrosiana, Rozzano (MI), 2013.
[100]Napolitano M, Orlandi P. Laminar flow in a complex geometry: a comparison[J]. International Journal for Numerical methods in Fluids, 1985, 5: 667-683.
[101]Roache P. Scaling of high Reynolds number weakly separated channel flows[M]//Cebeci T. Numerical and physical aspects of aerodynamic flows. Springer Science+Business Media, LLC. 1982: 87-98.
[102]Baines M J. Introduction to “approximate Riemann solvers, parameter vectors, and difference schemes”[J]. Journal of Computational Physics, 1997, 135 (2): 249.
[103]Roe P L, Baines M J. Asymptotic behaviour of some non-linear schemes for linear advection[J]. Notes on Numerical Fluid Mechanics, 1983, 7: 283-290.
[104]Roe P L. Characteristic-based schemes for the Euler equations[J]. Annual Review of Fluid Mechanics, 1986, 18 (1): 337-365.
[105]Struijs R, Deconinck H, Roe P L. A multidimensional generalization of Roe's flux difference splitter for the Euler equations[J]. Computers & fluids, 1993, 22 (2-3): 215-222.
[106]Van Leer B. A choice of difference schemes for ideal compressible flow[R]. Thesis, Sterrewacht, Leiden, The Netherlands, 1970.
[107]Roe P L. The use of the Riemann problem in finite difference schemes[M]// Reynolds W C, MacCormak R W. Lecture Notes in Physics 141. Springer-Verlag, 1980: 354-359 (Proceedings of the 7thICNMFD).
[108]Van Leer B. Towards the ultimate conservative difference scheme. I. The quest for monotonicity[M]// Cabannes H, Temam R. Lecture Notes in Physics 18. Springer-Verlag, 1973: 163-168 (Proceedings of the 3rdICNMFD).
[109]Van Leer B. Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme[J]. Journal of Computational Physics, 1974, 14 (4): 361-370.
[110]Van Leer B. Towards the ultimate conservative difference scheme. III. Upstream-centered finite difference schemes for ideal compressible flow[J]. Journal of Computational Physics, 1977, 23 (3): 263-275.
[111]Van Leer B. Towards the ultimate conservative difference scheme. IV. A new approach to numerical convection[J]. Journal of Computational Physics, 1977, 23 (3): 276-299.
[112]Van Leer B. Towards the ultimate conservative difference scheme. V. A second order sequel to Godunov’s method[J]. Journal of Computational Physics, 1979, 32 (1) : 101-136.
[113]Boris J P, Book D L. Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works[J]. Journal of Computational Physics, 1973, 11 (1): 38-69.
[114]Van Leer B. A historical oversight: Vladimir P. Kolgan and his high-resolution scheme[J]. Journal of Computational Physics, 2011, 230 (7): 2378-2383.
[115]Kolgan V P. Application of the principle of minimizing the derivative to the construction of finite-difference schemes for computing discontinuous solutions of gas dynamics[J]. Journal of Computational Physics, 2011, 230 (7): 2384-2390.
[116]Van Leer B. Flux-vector splitting[M]//Krause E. Lecture Notes in Physics 170. Springer-Verlag, 1982: 507-512. (Proceedings of the 8th ICNMFD).
[117]Thomas J L, Walters R W, Van Leer B. Implicit flux-split schemes for the Euler-equations[R]. AIAA-85-1680, 1985.
[118]Anderson W K, Thomas J L, Van Leer B. Comparison of finite-volume flux-vector splittings for the Euler equations[J]. AIAA Journal, 1986, 24: 1453-1460.
[119]Harten A, Lax P D, Van Leer B. Upstream differencing and Godunov-type schemes for hyperbolic conservation laws[J]. SIAM Review, 1983, 25:35-61.
[120]Van Leer B. Upwind-difference methods for aerodynamic problems governed by the Euler equations[M]// Engquist B, Osher S, Somerville R C J. Large-scale computations in fluid mechanics. Lectures in Applied Mathematics, Part 2 (A85-48201 23-34), Providence, R. I. :American Mathematical Society, 1985: 327-336. (Proceedings of the Fifteenth Summer Seminar on Applied Mathematics, La Jolla, CA, June 27-July 8, 1983).
[121]Mulder W A, Van Leer B.Experiments with implicit upwind methods for the Euler equations[J]. Journal of Computational Physics 1985, 59: 232-246; AIAA-83-1930-CP, 1983.
[122]Roe P L, Le Veque R, Van Leer B. A one-sided view[M]// Hafez M M, Chattot J -J. Innovative methods for numerical solutions of partial differential equations. World Scientific, 2002: 1-10.
[123]Van Leer B. Progress in multidimensional upwind differencing[M]//Lecture Notes in Physics 414, Napolitano M, Sabetta F., Springer-Verlag, 1993: 1-26. (Proceedings of the 13thICNMFD).
[124]Dadone A, Napolitano M. Unsteady flows through screens[J]. Meccanica, 1974, 9: 165-171.
[125]Napolitano M, Werle M J, Davis R T. Numerical solutions for high Reynolds number separated flow past a semi-infinite compression corner[J]. Computers & Fluids, 1979, 7:165-175.
[126]Napolitano M, Werle M J, Davis R T. A numerical technique for the triple-deck problem[J]. AIAA Journal, 1979, 17 (7): 699-705.
[127]Napolitano M. A numerical study of strong slot injection into a supersonic laminar boundary layer[J]. AIAA Journal, 1980, 18 (1): 72-77.
[128]Napolitano M, Messick R E. On strong slot injection into a subsonic laminar boundary layer[J]. Computers & Fluids, 1980, 8: 199-212.
[129]Napolitano M. Efficient ADI and spline ADI methods for the Navier-Stokes equations[J]. International Journal on Numerical Methods in Fluids, 1984, 4 : 1101-1115.
[130]Napolitano M, Walters R W. An incremental block-line-Gauss-Seidel method for the Navier-Stokes equations[J]. AIAA Journal, 1986, 24 (5): 770-776. Originally presented at the 21st annual meeting of the Society of Engineering Science, Inc., October 15-17, 1984. Virginia Tech, Blacksburg, VA, USA.
[131]Mac Cormack R W, Candler G V. The solution of the Navier-Stokes equations using Gauss-Seidel line relaxation[J]. Computers & Fluids, 1989, 17: 135-150.
[132]Napolitano M. An incremental multigrid strategy for the fluid dynamic equations[J]. AIAA Journal, 1986, 24 (12): 2040-2042.
[133]Napolitano M. Efficient solution of two-dimensional incom-pressible steady separated flows[J]. Computers & Fluids, 1991, 20: 213-222. Invited lecture at the second ISCFD Sydney, 1987.
[134]Morrison J H, Napolitano M. Efficient solutions of two-dimensional incompressible steady flows[J]. Computers & Fluids, 1988, 16 (2):119-132.
[135]Napolitano M, Cinnella P. A numerical study of two-dimensional and axially-symmetric sudden expansion flows[J].Computers & Fluids, 1989, 17 (1):185-193.
[136]Dadone A, Napolitano M. A perturbative lambda formulation[J]. AIAA Journal, 1986, 24: 411-417.
[137]Napolitano M. Simulation of compressible inviscid flows: the Italian contribution[R]. Lecture Notes in Physics 264, Springer-Verlag, 1986: 47-56 (Proceedings of the 10thICNMFD).
[138]Pascazio G, Napolitano M. A staggered-grid finite volume method for the vorticity-velocity equations[J].Computers & Fluids, 1996, 25 (4) : 433-446.
[139]Giannattasio P, Napolitano M. Optimal vorticity conditions for the node-centred finite-difference discretization of the second-order vorticity-velocity equations[J]. Journal of Computational Physics, 1996,127: 208-217.
[140]Grimaldi A, Pascazio G, Napolitano M. A parallel multi-block method for the unsteady vorticity-velocity equations[J]. CMES: Computer Methods in Engineering and Sciences, 2006,14 (1): 45-56.
[141]Catalano L A, De Palma P, Napolitano M, et al. A critical analysis of multidimensional upwinding for the Euler equations[J]. Computers & Fluids, 1996, 25 (1): 29-38.
[142]De Palma P, Pascazio G, Rubino D T, et al. Residual distribution schemes for advection and advection-diffusion problems on quadrilateral cells[J]. Journal of Computational Physics, 2006, 218 (1) : 159-199.
[143]Rossiello G, De Palma P, Pascazio G, et al. Second-order-accurate explicit fluctuation splitting schemes for unsteady problems[J].Computers & Fluids, 2009, 38 (7) : 1384-1393.
[144]Rossiello G, De Palma P, Pascazio G, et al. Third-order-accurate fluctuation splitting schemes for unsteady hyperbolic problems[J]. Journal of Computational Physics, 2007, 222 (1): 332-352.
[145]De Palma P, De Tullio M D, Pascazio G, et al. An immersed-boundary method for compressible viscous flows[J]. Computers & Fluids, 2006, 35 (7): 693-702.
[146]De Palma P, Valentini P, Napolitano M. Dissipative particle dynamics simulation of a colloidal micropump[J].Physics of Fluids 2006, 18: 027103-1-12.
[147]Cutrone L, De Palma P, Pascazio G, et al. Predicting transition in two- and three-dimensional separated flows[J]. International Journal of Heat and Fluid Flow, 2008, 29 (2): 504-526.
[148]Cutrone L, De Palma P, Pascazio G, et al. A RANS flamelet-progress-variable method for computing reacting flows of real-gas mixtures[J]. Computers & Fluids, 2010, 39 (3): 485-498.
0258-1825(2016)02-0139-18
欧洲计算流体力学——个人观点
M. Napolitano*
(Department of Mechanics, Mathematics and Management, Polytechnic of Bari, Via Orabona 4, 70125, Bari, Italy)
介绍了70年代初到20世纪末欧洲科学家对CFD发展的主要贡献,并重点关注了对国际流体力学数值方法会议(ICNMFD)和国际计算力学学术会议(ISCFD)的成功举办具有重大贡献的科学家。ICNMFD始于1969年(新西伯利亚),由参与了美国和苏联太空竞赛的两国科学家联合创办,而ISCFD则作为ICNMFD在亚太地区的同类会议初创于1995年(东京)。由Oshima教授和本人提议,得益于上述两个会议全体科学委员会成员的共同努力,ICNMFD和ISCFD自2000年开始,合并成为每两年举办一次的国际计算流体力学会议(ICCFD)。绝大部分本文讨论所涉及的学者通常都在受邀进行大会报告后,成为了前述三大国际会议中的一个或多个科学委员会的成员。作者对文中讨论所涉及的研究人员的圈定负有全权责任,上述人员的选择更多地基于应用而非理论计算流体力学,因此尚存在不完善之处。此外由于文中所讨论的学者大都是作者在40多年计算流体力学研究生涯中的私交好友,因此并没有将年轻一代的科学家考虑进来,但这并非由于他们的贡献不重要。另外值得注意的是欧洲的计算流体力学同美国的计算流体力学有非常紧密的联系,本文讨论所涉及的研究学者有些最早从欧洲开始涉足计算流体力学而现在则生活和工作于美国(例如Glowinski, Roe, Van Leer等人),而有些则是在美国取得了博士学位(例如Launder, Napolitano),他们都同美国的科学家进行过合作,因此很难清晰地对欧洲和美国的计算流体力学进行界定。对那些现已移居美国的欧洲科学家们,本文优先考虑了他们移居之前的贡献。最后但并非是最不重要的,作者通过电子邮件一一联系了文中所涉及的科学家,希望他们本人能够给出其自身贡献的评价草稿,从而帮助作者以最权威的视角在文中相应章节对其工作进行评述。本文向提供自述评价的诸位致以谢意,同时也希望其他同仁能够对本人不恰当的擅自评述给予谅解。
计算流体力学; 直接数值模拟; 有限差分; 有限元; 有限体积; 通量差分分裂; 通量矢量分裂; 高阶格式; 大涡模拟; Lax-Wendroff格式; 多重网格; 粒子流动; 湍流模型
V211.3
A doi: 10.7638/kqdlxxb-2016.0011
*Professor; michele.napolitano@poliba.it
format: Napolitano M. Computational Fluid Dynamics in Europe, a personal view[J]. Acta Aerodynamica Sinica, 2016, 34(2): 139-156.
10.7638/kqdlxxb-2016.0011. Napolitano M. 欧洲计算流体力学——个人观点(英文)[J]. 空气动力学学报, 2016, 34(2): 139-156.
Received date: 2016-02-04; Revised date:2016-03-15
- 空气动力学学报的其它文章
- The History of CFD in China
- Simulations of Transonic Flows withFriction and Heat Addition
- Coupled CFD/RBD Modeling for a BasicFinner Projectile with Control
- High Order Numerical Methods for LESof Turbulent Flows with Shocks
- Vorticity Dynamics and Control of Self-PropelledFlying of a Three-Dimensional Bird
- Residual Schemes Applied to an Embedded MethodExpressed on Unstructured Adapted Grids

