缺失数据下基于EM算法的非线性过程建模

王幼琴，赵忠盖，刘飞（江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122）



缺失数据下基于EM算法的非线性过程建模

王幼琴，赵忠盖，刘飞
（江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122）

摘要：线性时变参数系统（LPV）将多阶段、非线性的过程建模转化为线性多模型的辨识问题，近年来得到了极大关注。考虑缺失数据下LPV系统的离线建模问题，首先引入一个二进制变量表征输出样本缺失状态，选取过程关键变量作为调度变量，确定主要工况点；然后围绕不同工况点建立局部子模型，将输出缺失部分和采样数据的模型归属当作隐藏变量，利用EM算法进行参数估计，再采用高斯权重函数融合各子模型。最后分别针对典型二阶过程和连续搅拌反应釜（CSTR），运用提出的多模型和算法进行仿真实验，表明有效性。

关键词：非线性过程；LPV系统；多模型；缺失数据；EM算法；参数估计

2015-06-12收到初稿，2015-09-08收到修改稿。

联系人：刘飞。第一作者：王幼琴（1991—），女，硕士研究生。基金项目：国家自然科学基金项目（61134007，61573169）。

引 言

非线性过程的建模一直是学术界和工业界的关注焦点。过去几十年，非线性过程建模技术得到了极大发展，归纳起来，主要包括黑箱建模和机理建模方法。黑箱建模方法通过分析过程的历史数据，建立过程变量之间的相关模型。常见的黑箱模型有人工网络模型，非线性自动回归模型（NARX），高斯回归过程和混杂模型[1-4]，这些建模方法均不需深入了解过程的反应机理，对数据的数量和质量依赖性强。机理建模方法根据过程运行机理，通过能量/质量守恒定理建立过程非线性模型，精度高。但该方法基于对过程机理的深入了解，建模周期长，难度大。

LPV（liner parameter varying）系统，也称为线性变参数系统，通过线性模型参数变化，也即线性多模型系统逼近复杂非线性系统，其模型描述形式具有线性系统的特点，模型系数矩阵是关于一个调度变量的函数。调度变量一般选取实际工业过程中可测量且反映不同阶段特征的过程关键变量[5]。近年来LPV建模得到极大关注[6-9]，Bamieh等[6]提出了一种假设输入-输出数据和调度变量都可测量的LPV辨识模型，采用最小二乘方法估计参数，该方法要求在整个大范围工作点进行长时间测试，难以适用于部分输入信号不能操纵的过程。为了降低对输入信号的要求，Zhu等[9]提出一种基于调度变量操作轨迹LPV模型的非线性辨识方法，只在特定工作点进行测试与辨识相应模型，并根据工作点测试数据及各工作点间过渡数据辨识全局插值LPV模型。然而，该方法中所有的局部先验模型都要求已知，且全局辨识模型的性能容易受到各个局部模型精度的影响。此外，该方法采用三次样条函数作为权重函数融合子模型，而确定三次样条函数合适的阶数也具有一定的难度。Jin等[10]将EM算法引入LPV模型的辨识中，利用EM算法对局部模型进行辨识，并采用高斯权函数合成局部模型。EM算法是基于极大似然的参数估计方法，是一种当观测数据为不完全数据时求解最大似然估计的迭代算法，能够有效处理多模型建模问题[11-12]。在Jin等的研究基础上，Chen等[13]继续研究了调度变量受噪声干扰的非线性系统，引入状态空间模型来描述调度变量的动态特性，应用多模型方法及期望最大化（EM）算法辨识过程模型。

但是，上述方法仅仅考虑了测量值完全可测的情形。而在实际工业过程中，由于恶劣的环境、传感器故障等原因，测量值缺失情况普遍存在。缺失值从缺失的分布来讲可以分为完全随机缺失（MCAR）、随机缺失（MAR）和完全非随机缺失（MNAR）[14]，对于缺失数据的处理方法主要有两大类：缺失值删除法和缺失值插补法[15]。删除法就是将含有缺失值的样本直接舍弃，方法简单，缺失的变量值占总体数据的总量很小的情况下使用该方法比较有效，但该方法最大的缺点就是可能会丢失有效信息，不适合用于采样频率低、采样数据少的过程。缺失值插补法包括均值插补、极大似然估计、多重插补等方法。该方法对于缺失类型是随机缺失的效果较好，但也存在对样本存在干扰的缺点。

本文主要考虑测量值缺失的情况下非线性系统的辨识问题，假设输出缺失类型属于MCAR或者MAR，并选用基于极大似然估计的EM算法处理缺失数据。首先引入一个二进制变量H表征每一时刻输出是否缺失，同时选取过程中的关键变量作为调度变量，确定主要的工况点并进行子模型的划分，子模型结构采用能较好逼近任意线性动态系统的ARX模型。然后基于EM算法，将采样数据的模型归属以及输出数据缺失部分当作隐藏变量，对子模型参数进行估计，最后通过符合高斯分布的权重函数合成全局模型。针对典型二阶非线性过程和CSTR系统分别进行仿真实验，结果表明该方法具有较高的拟合精度。

1 基于EM算法的多模型建模

本文中用一组ARX模型作为局部线性模型来逼近过程的动态[16]。ARX模型具有较好的逼近线性动态系统的性能，表示如下

假设工况点个数记为M，即子模型的个数，每个工作点处的调度变量记为τi本质上是非线性过程局部线性化的操作条件，在实际生产过程中，操作阶段明确，因此此处τi假设已知。

为使各子模型平滑融合，采用高斯分布函数为权重函数[17]，k时刻第i个子模型的权重wki表示如下

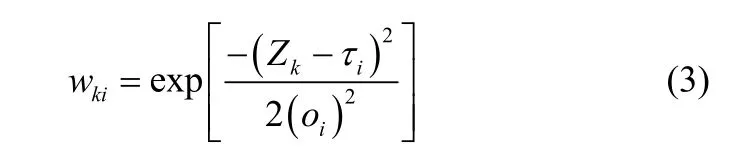
式中，Zk表示k时刻调度变量的值；oi表示第i个模型的有效宽度。归一化后的权重函数可以表示为

因此，对于输出的预测可以表示如式（5）所示

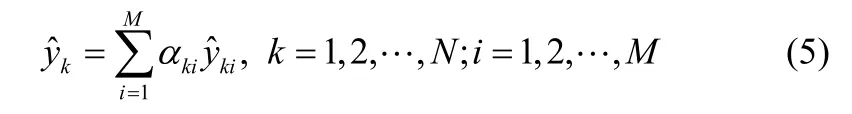
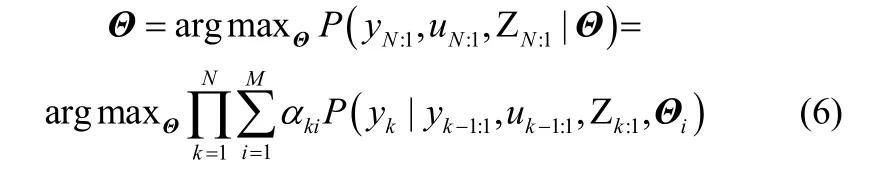
2 缺失数据下基于EM算法的参数估计

EM算法由Dempster等[18]于1977年提出，旨在求解数据有缺失或隐含情况下参数的极大似然估计。EM算法由E（expectation）步和M（maximization）步组成。E步利用对隐藏变量的现有估计值和可观测数据，计算完整数据的对数似然函数的期望，记为Q函数；M步中，通过最大化Q校正参数向量。

E步和M步不断迭代直至似然函数收敛。Cobs和缺失数据Cmis两部分组成，即记输出可测部分为yobs，输出缺失部分为ymis，则整个过程的输出为，可观测数据集，不可观测部分为，过程中完整的数据集可以表示为，其中。

则EM算法可以归纳为以下步骤[12]：

（1）初始化参数向量Θold；

（2）E步，使用当前参数Θold估计近似的Q函数

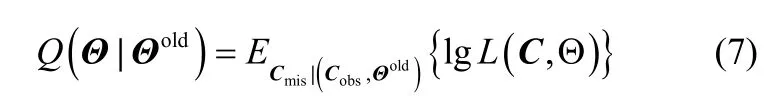
（3）M步，将Q函数最大化，获得新的迭代参数

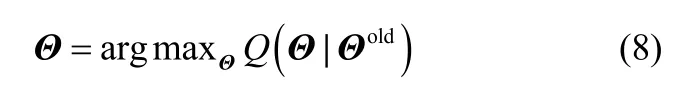
（4）迭代过程，将获得新的参数代入步骤（2），不断重复步骤（2）和步骤（3），直至满足收敛条件。

下面详细介绍本文在输出有缺失的情况下EM算法的计算步骤。

（1）E步

利用隐藏变量的现有估计值和可观测数据求完整数据集C期望的表达式如式（9）所示。

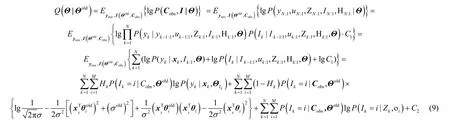
为了进一步计算式（9）中的Q函数，则需要计算P( yk|xk, ΘIk)，和这3个概率密度函数。表示的是ARX模型分布概率，符合高斯分布，根据高斯分布概率函数可以得到，如式（10）所示

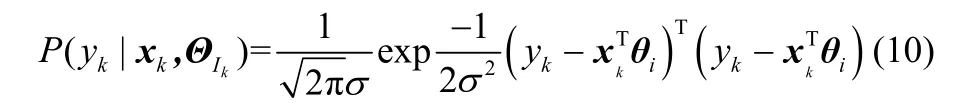
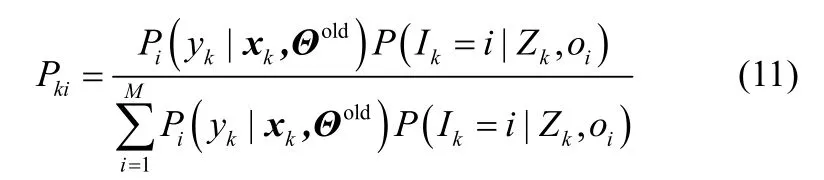
详细推导见附录3。

（2）M步

M步就是将E步中得到的Q函数极大化，获得新的参数。分别针对子模型参数θi和过程噪声方差σ2求偏导得到

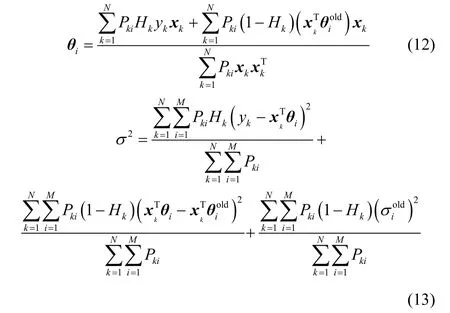
对于局部模型有效宽度oi，由于采用指数函数形式作为权函数来合成模型，在对式（9）中Q函数进行优化时不能得到它的解析形式，可以转化为有约束情况下的极值求解问题，该最优值问题可描述为

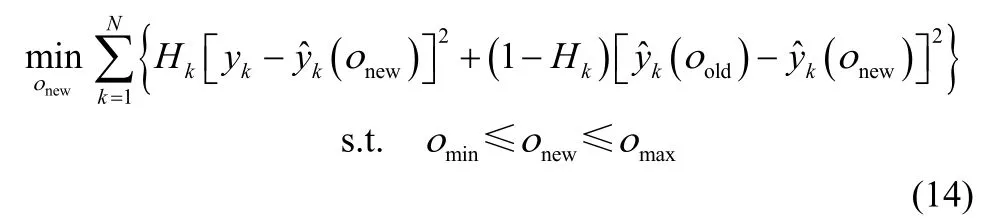
根据式（12）～式（14）得到当前的参数、噪声方差和子模型有效宽度的估计，将其代入Q函数进行下一次迭代，直至收敛。

3 建模验证

3.1 数值仿真试验

以模型参数变化的二阶过程为例，验证前述LPV建模方法，二阶过程的传递函数如式（15）

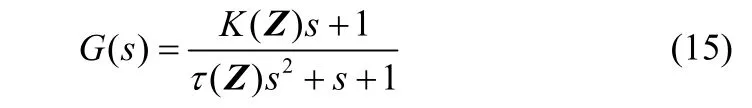
该过程增益K(Z)和过程时间常数τ(Z)均为调度变量Z的非线性函数，具体的非线性关系式如下：

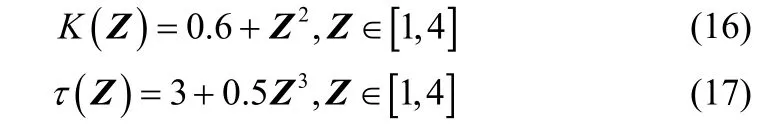
可以看出，在整个过程的操作范围内，过程增益和时间常数的变化比较剧烈，在特定工作条件下的单一线性模型难以捕捉整个工作范围内的动态特性。因此采用基于LPV系统的多模型描述在不同操作条件下的过程行为。

采用多模型对LPV系统建模时，假设在Z1= 1、Z2= 2.5、Z3= 4这3个工作点进行测试，测试信号为幅值0.5的随机二进制信号。在两个工作点的过渡期间，调度变量Z以固定的步长增加。同时在获取的输出数据中加入了方差为0.15的过程白噪声，输出数据随机缺失。

图1表示实际的输入输出信号，图2表示整个过程中调度变量的轨迹。输出缺失50%时二进制数Hk如图3所示。图4表示了归一化后的权重与调度变量之间的关系。当输出数据缺失50%时，模型自我验证的结果如图5所示。模型的质量通过相关误差量测[17]

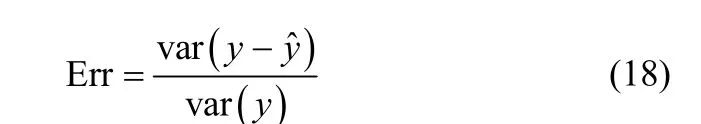
图1 输入输出信号(理论值)Fig.1 Input-output excitation data

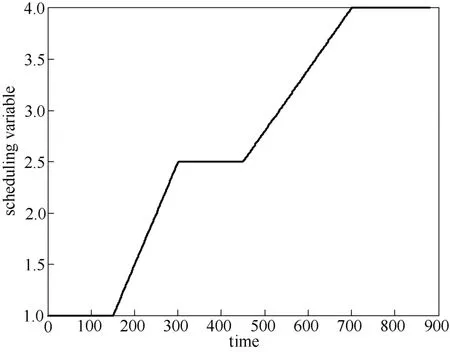
图2 二阶非线性过程调度变量的值Fig.2 Scheduling variable of second-order nonlinear process

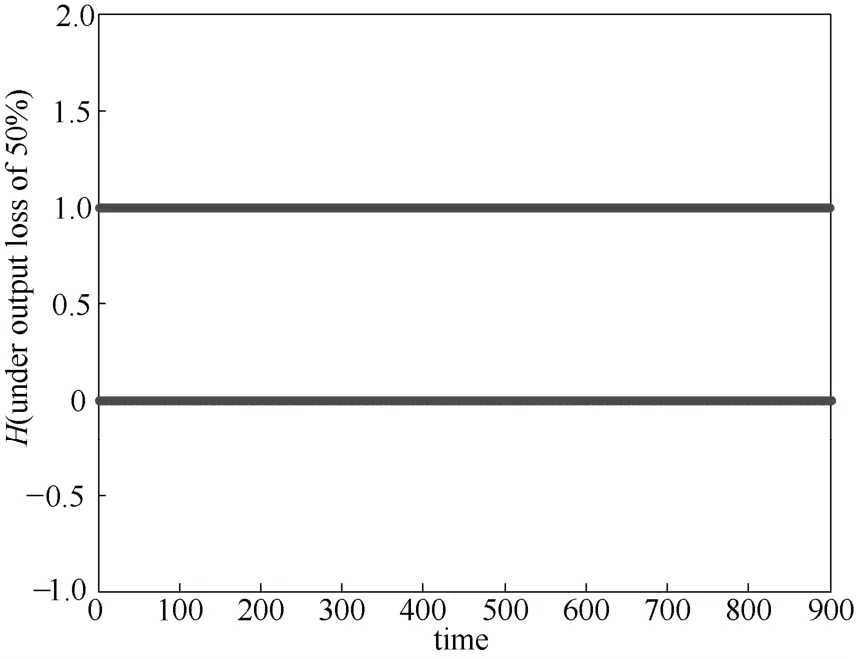
图3 输出缺失50%时二进制变量Hk的值Fig.3 Value of binary variables under output loss of 50%

3.2 CSTR仿真实验

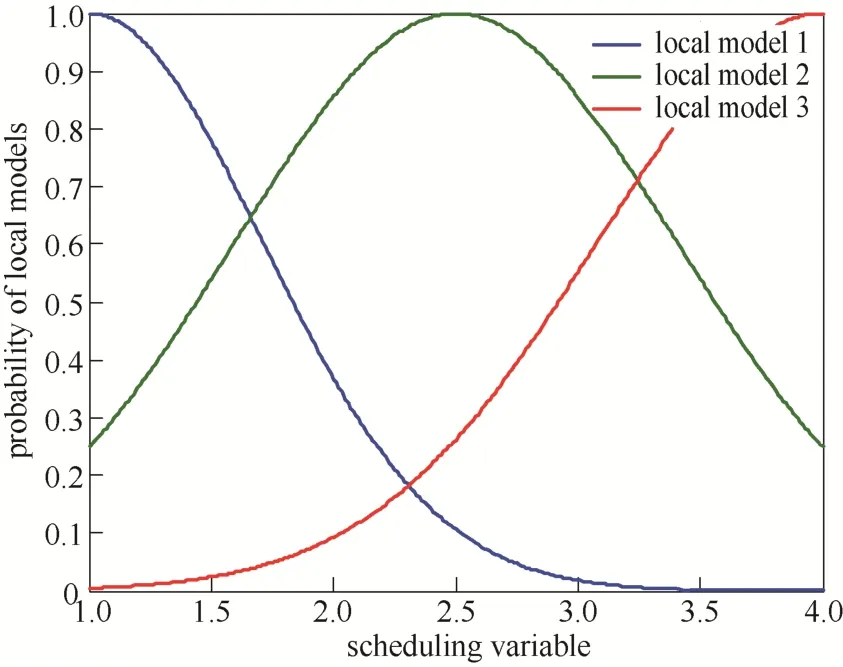
图4 二阶非线性过程不同操作点下的子模型权重Fig.4 Weight of each local model at different operating points of second-order nonlinear process

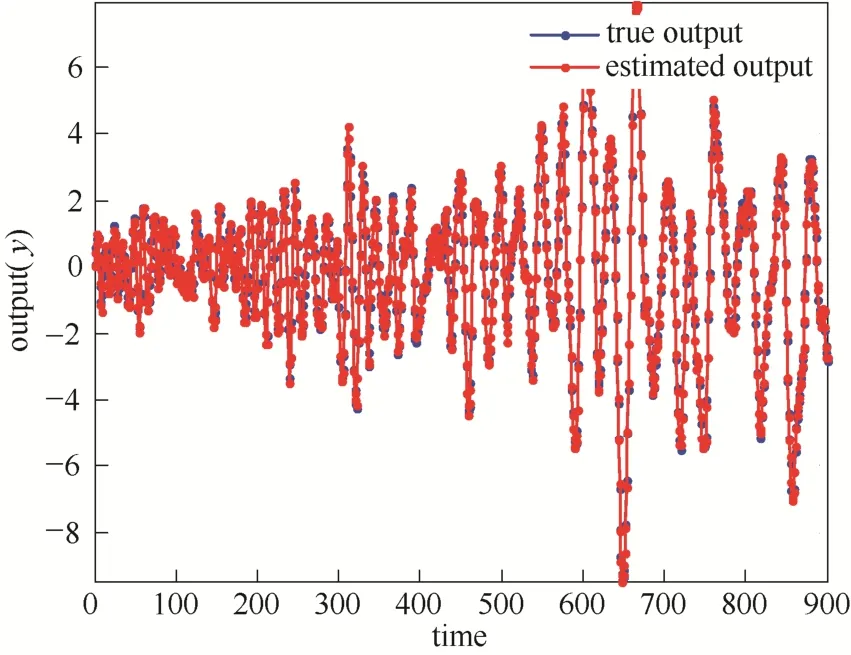
图5 二阶非线性过程自我验证输出预测Fig.5 Validation of global model against model training data set of second-order nonlinear process

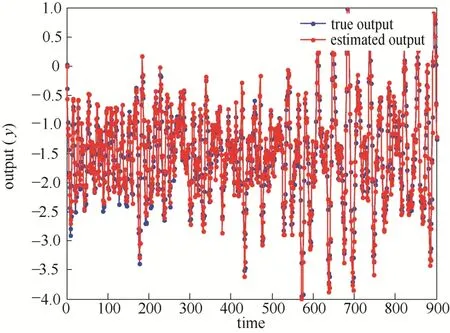
图6 二阶非线性过程交叉验证输出预测Fig.6 Cross validation of identified global model of second-order nonlinear process

表1 ARX子模型的真实参数Table 1 Real parameters of ARX model

连续搅拌反应釜（continuous stirred tank reactor， CSTR）是发酵、化工、石油生产、生物制药等工业生产过程中应用最广泛的一种化学反应器，CSTR的化学反应过程是一个非线性、时变的过程，对这类系统难以建立精确的机理模型。在本文中，采用的是不可逆放热反应过程A→B[10,19-20]。如图7所示是一个装有冷却管的连续搅拌反应槽（CSTR）。进入CSTR的过程流量为q，温度为T0，密度为ρ，A物质浓度为CA0，冷却液温度为Tc0，流量为qc，介质密度为ρc。物料在反应槽中充分搅拌并发生化学反应，产生的热量由冷却器带走。最后生成的产品溢流出去，产品A最终的浓度为CA。

表2 不同缺失数据下ARX子模型的参数估计值Table 2 Estimated parameter of ARX model under missing output

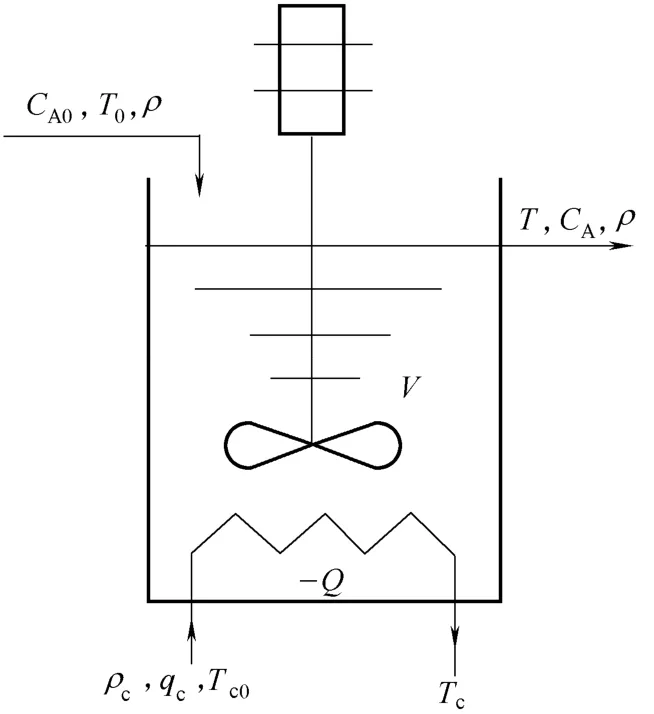
图7 具有冷却器的连续搅拌反应槽Fig.7 Continuous stirring tank reaction

根据质量和热量守恒定律，该过程的第一原理模型可以表示为

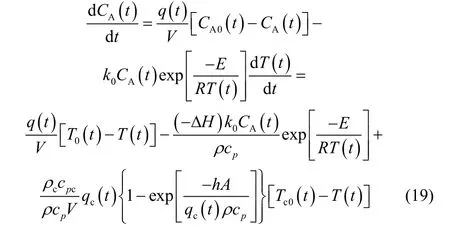
式（19）中各项变量及其相应的稳态值见表3。

本文中，反应器内A产品浓度为主要输出，冷剂流量qc为输入变量同时也为调度变量，其范围为97～105 L·min−1，预先选定97、100、101、103、105 L·min−15个工作点。

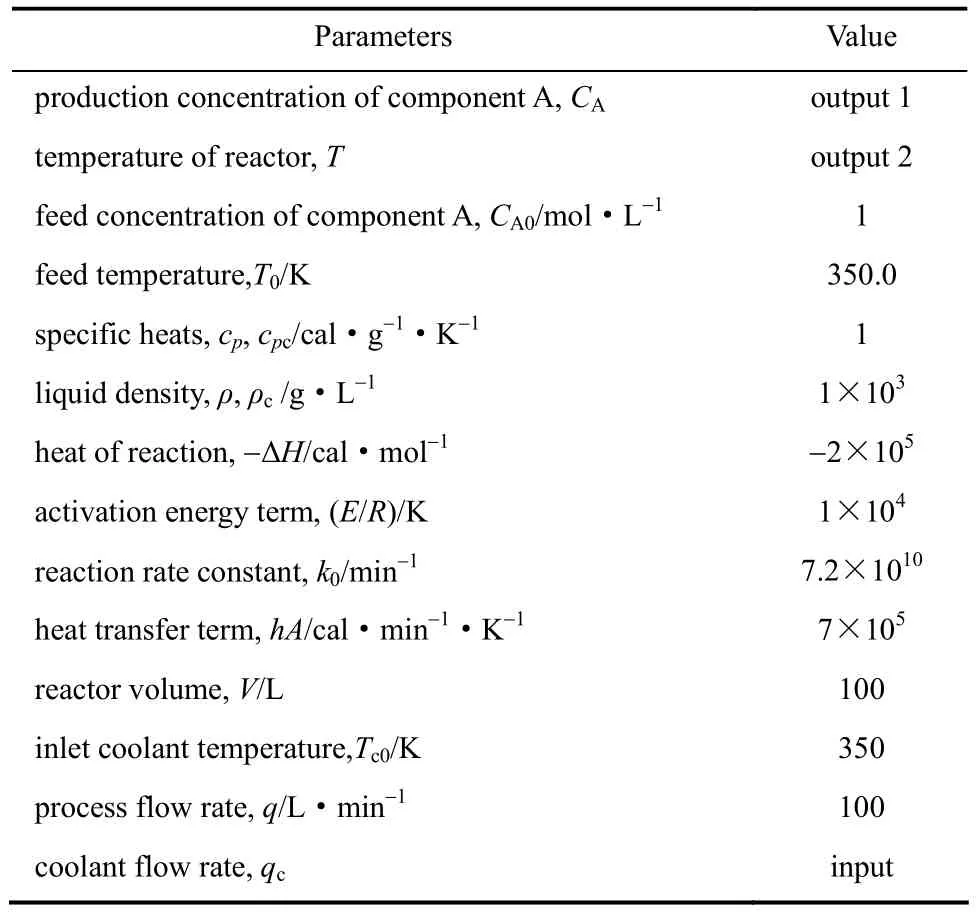
表3 CSTR模型参数及稳态值Table 3 CSTR model parameters and their steady state values

图8所示的是输入-输出数据，由图中可以看出输入包含了5个工作点，在每个操作点时输入是幅值为1的随机二进制信号，同时在每两个操作点之间，冷剂流量以固定步长增加。图9表示的是整个操作范围内的调度变量的值。图10表示的是归一化后的权重，图11为输出缺失25%时自我验证，可以看出预测输出和真实输出拟合效果较高。为了进一步验证模型有效性，选取另一组数据进行交叉验证。图12为交叉验证，图13为预测输出和真实输出的分布，可以看出预测输出较好的拟合真实输出。从图11～图13可以看出根据本文所述方法建立的模型拟合精度较高。根据式(18)计算得到的自我验证的相关误差为1.14%，交叉验证的相关误差为1.72%。

4 结 论

针对输出存在缺失的非线性工业过程，引入二进制变量表示输出的有效性，选取过程关键变量作为调度变量，将模型归属以及输出缺失部分当作隐含变量，采用基于EM算法的多模型方法建模。子模型结构采用ARX模型，同时将归一化的指数函数作为权重函数，用来表示每个局部模型有效的概率并将所有的局部模型合成。最后对二阶非线性过程和CSTR系统分别进行仿真实验，结果表明本文方法下的建模精度较高。

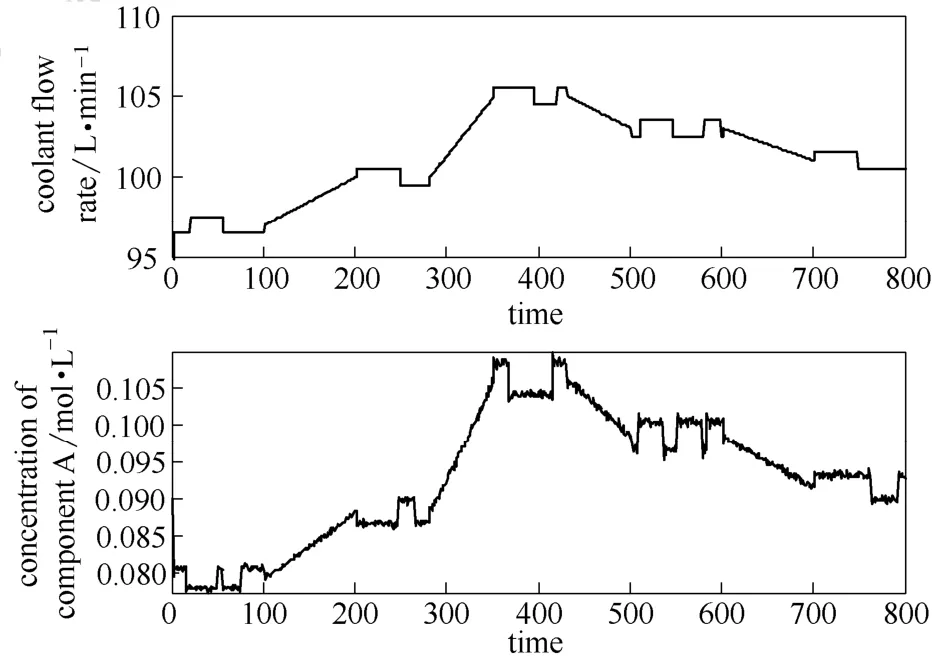
图8 CSTR系统的输入-输出Fig.8 Input-output excitation data of CSTR system

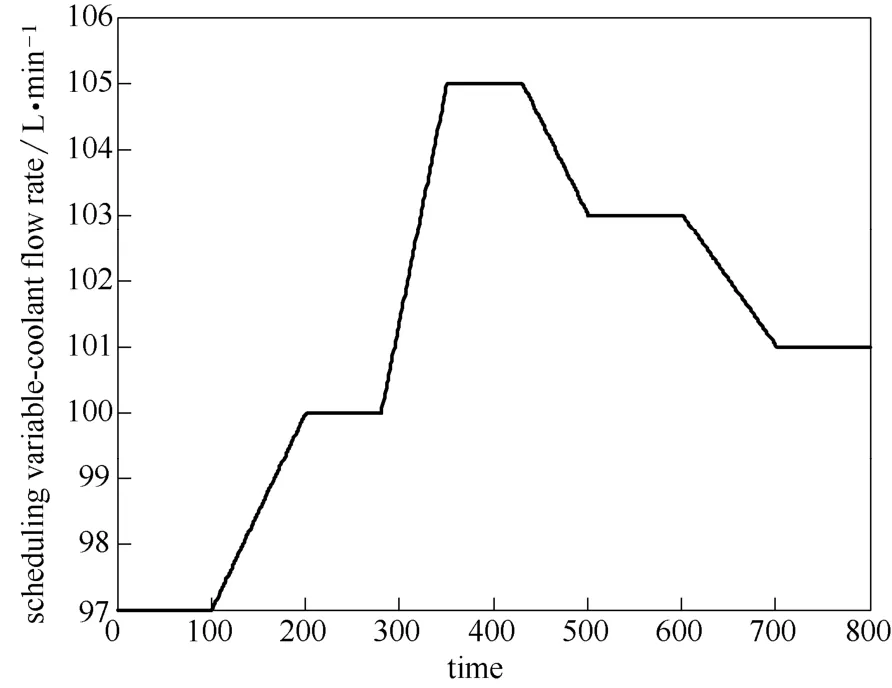
图9 CSTR系统调度变量的值Fig.9 Scheduling variable of CSTR system

图10 CSTR系统不同操作点下的子模型权重Fig.10 Weight of each local model at different operating points

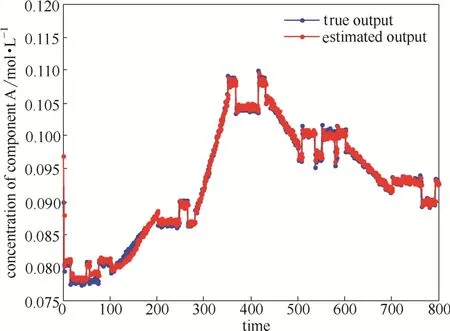
图11 CSTR系统自我验证输出预测Fig.11 Validation of global model against model training data set of CSTR system

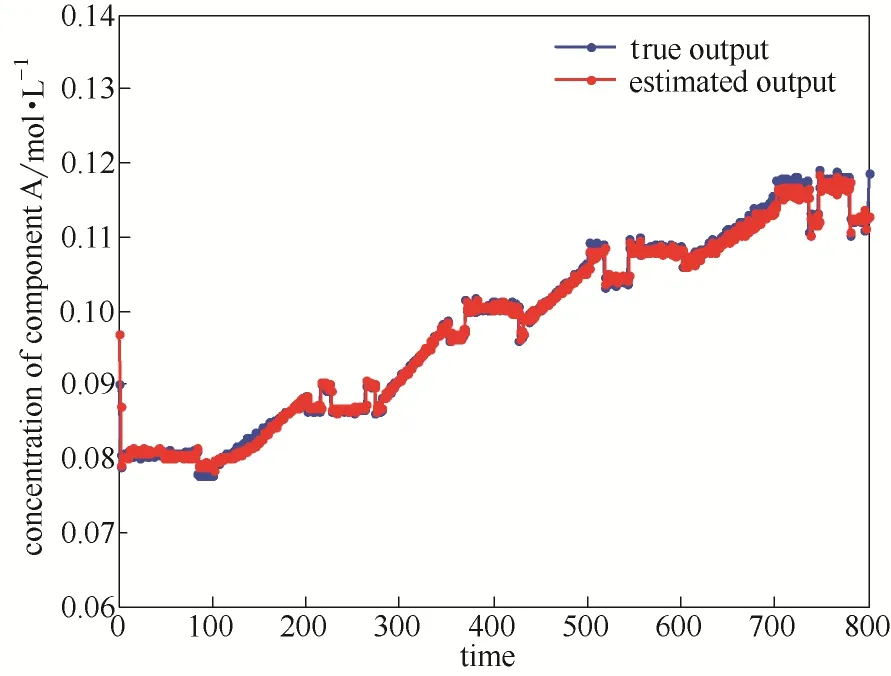
图12 CSTR系统交叉验证输出预测Fig.12 Cross validation of identified global model of CSTR system

图13 交叉验证预测输出分布Fig.13 Output forecast maps under cross validation

References

[1] PICHE S, SAYYAR R B, JOHNSON D, et al. Nonlinear modelpredictive control using neural networks [J]. IEEE Control Systems, 2000, 20 (3): 53-62.

[2] HENSON M A. Nonlinear model predictive control: current status and future directions [J]. Computers & Chemical Engineering, 1998, 23 (2): 187-202.

[3] RASMUSSEN C E. Gaussian Processes in Machine Learning [M]. Berlin: Springer Berlin Heidelberg, 2004: 63-71.

[4] WANG X F, CHEN J D, LIU C B, et al. Hybrid modeling of penicillin fermentation process based on least square support vector machine [J]. Chemical Engineering Research and Design, 2010, 88 (4): 415-420.

[5] ZHU Y C, XU Z H. A method of LPV model identification for control [J]. IFAC Proceedings Volumes (IFAC-Papers Online), 2008, 17 (1): 5018-5023.

[6] BAMIEH B, GIARRE L. Identification of linear parameter varying models [J]. International Journal of Robust and Nonlinear Control, 2002, 12 (9): 841-853.

[7] LEE L H, POOLLA K. Identification of linear parameter varying systems using nonlinear programming [J]. Journal of Dynamic Systems, Measurement, and Control, 1999, 121 (1): 71-78.

[8] JOHANSEN T A, FOSS B A. Multiple model approaches to modelling and control [J]. International Journal of Control, 1999, 72 (7/8): 575-575.

[9] XU Z H, ZHAO J, QIAN J X, et al. Nonlinear MPC using an identified LPV model [J]. Industrial & Engineering Chemistry Research, 2009, 48 (6): 3043-3051.

[10] JIN X, HUANG B, SHOOK D S. Multiple model LPV approach to nonlinear process identification with EM algorithm [J]. Journal of Process Control, 2011, 21 (1): 182-193.

[11] JIN X, WANG S Y, HUANG B, et al. Multiple model based LPV soft sensor development with irregular/missing process output measurement [J]. Control Engineering Practice, 2012, 20 (2): 165-172.

[12] MCLACHLAN G J, KRISHNAN T. The EM algorithm and extensions [J]. Biometrics, 2008, 15 (1):154-156.

[13] CHEN L, TULSYAN A, HUANG B, et al. Multiple model approach to nonlinear system identification with an uncertain scheduling variable using EM algorithm [J]. Journal of Process Control, 2013, 23 (10): 1480-1496.

[14] KHATIBISEPEHR S, HUANG B. Dealing with irregular data in soft sensors: Bayesian method and comparative study [J]. Industrial & Engineering Chemistry Research, 2008, 47 (22): 8713-8723.

[15] DENG J, HUANG B. Identification of nonlinear parameter varying systems with missing output data [J]. AIChE Journal, 2012, 58 (11): 3454-3467.

[16] LJUNG L. System Identification: Theory for the User [M]. New Jersey: Birkhäuser Boston, 1987: 163-173.

[17] HUANG J Y, JI G L, ZHU Y C, et al. Identification of multi-model LPV models with two scheduling variables [J]. Journal of Process Control, 2012, 22 (7): 1198-1208.

[18] DEMPSTER A P, LAIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1977, 39 (1):1-38.

[19] HUANG Y L, LOU H H, GONG J P, et al. Fuzzy model predictive control [J]. IEEE Transactions on Fuzzy Systems, 2000, 8 (6): 665-678.

[20] MORNINGRED J D, PADEN B E, SEBORG D E, et al. An adaptive nonlinear predictive controller [J]. Chemical Engineering Science, 1992, 47 (4): 755-762.

附录1 式（6）推导过程

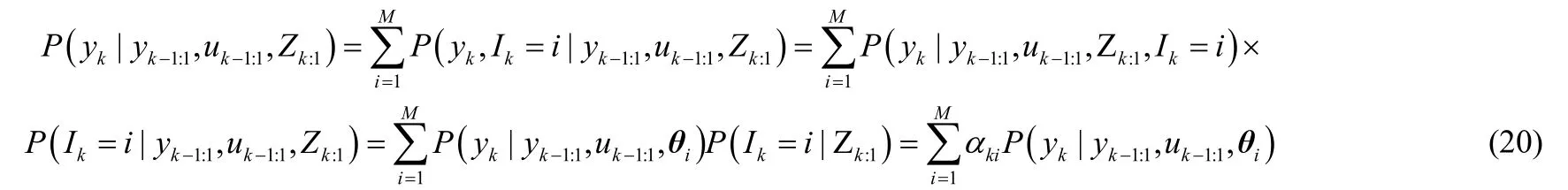
基于每个收集过程数据的局部模型身份可以由调度变量来推断的假设，故式（20）中存在等价。

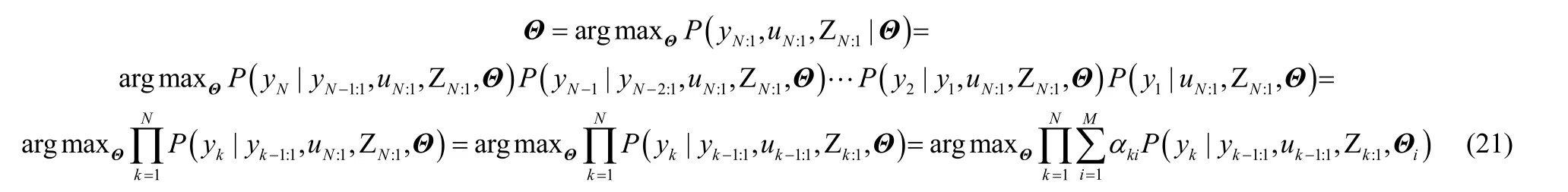
附录2 式（9）推导过程

从式（9）中可以看出要求Q函数，则需要求以下3项期望值：

下面将详细推导求期望值的过程，如下所示：

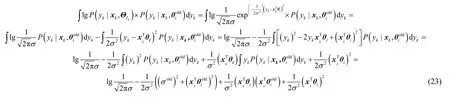
将式（23）代入式（22）中得到

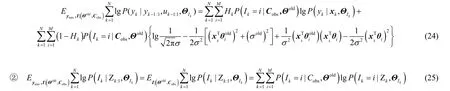
③因为C1为常数，故其期望也为常数，用C2表示，即将①、②和③中的期望相加即可得到Q函数，即

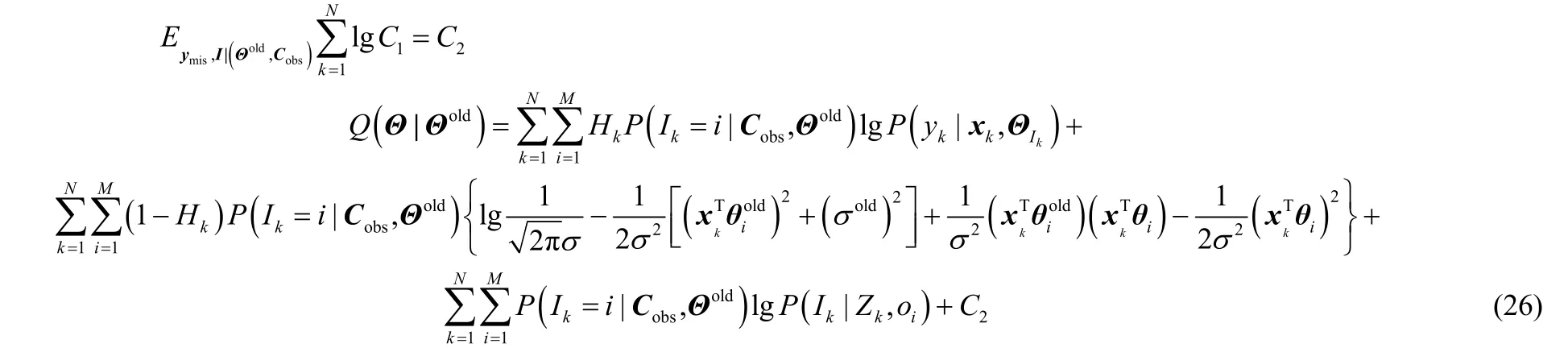
附录3 式（11）推导过程

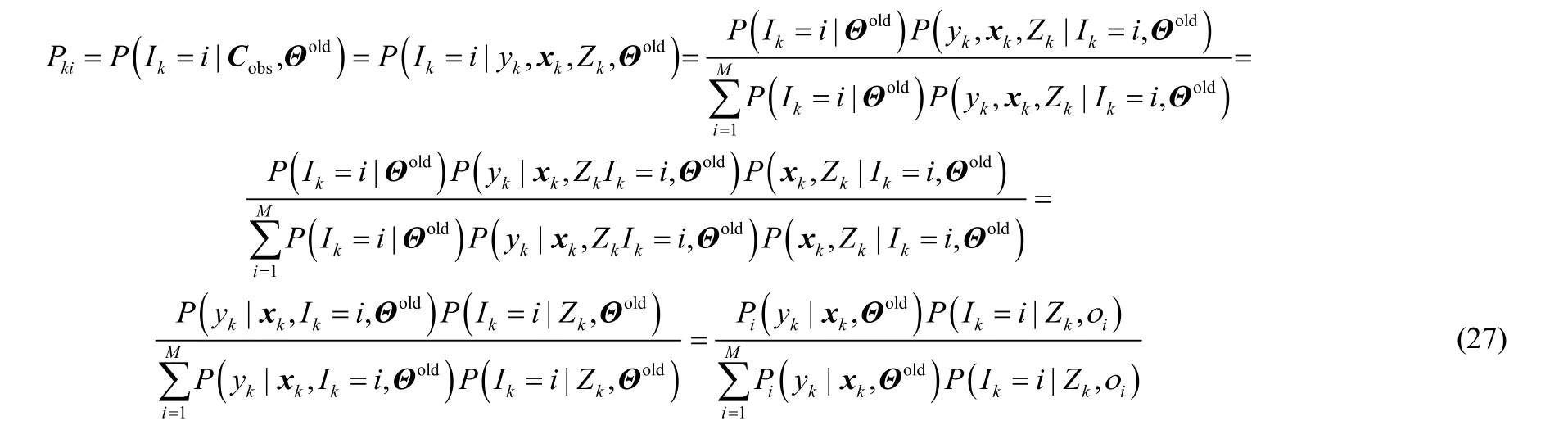
研究论文

Received date: 2015-06-12.

Foundation item: supported by the National Natural Science Foundation of China (61134007, 61573169).

Identification of nonlinear parameter varying systems with EM algorithm under missing output data

WANG Youqin, ZHAO Zhonggai, LIU Fei
(Key Laboratory of Advanced Control for Light Industry Processes of Ministry of Education, Jiangnan University, Wuxi 214122, Jiangsu, China)

Abstract:A linear parameter varying (LPV) method can develop the model of the multi-stage, non-linear process through the identification of linear multiple models. In recent years it has been of great concern. This paper investigates the identification of the LPV model with incomplete measurements. First, to indicate whether the output measurement is missing at each sampling instant, a binary variable is defined through which the availability of the output measurement is denoted. The key variable(s) can be taken as the scheduling variable(s) and the main operating point is determined based on the actual production process. Then, local models are constructed around each operating point, and EM algorithm is introduced to estimate their parameters. Both the missing data and the sampling data belonging are treated as the hidden variables. Finally, local models are combined according to an exponential weighting function. A simulated numerical example as well as the continuous stirred tank reactor (CSTR) are employed to demonstrate the effectiveness of the proposed method.

Key words:nonlinear process; LPV system; multiple models; missing data; EM algorithm; parameter estimation

DOI：10.11949/j.issn.0438-1157.20150917

中图分类号：TQ 028.8

文献标志码：A

文章编号：0438—1157（2016）03—0931—09

Corresponding author:Prof. LIU Fei, fliu@jiangnan.edu.cn