一种基于PWA模型的控制策略在连续搅拌反应釜中的应用

王宇红，杨璞（中国石油大学（华东）信息与控制工程学院，山东 青岛 266580）



一种基于PWA模型的控制策略在连续搅拌反应釜中的应用

王宇红，杨璞
（中国石油大学（华东）信息与控制工程学院，山东 青岛 266580）

摘要：在化工系统实际运行过程中，常常会出现一些不正常的工作状态，为了使系统运行状态能够避开这些不正常的工作状态，往往需要对控制器进行重构。针对这种情况，本文阐述了一种基于分段仿射模型的控制策略，该控制策略采用显式模型预测控制算法对系统进行控制，当检测到系统出现异常工作点时，先对系统进行形式验证，根据验证结果，再决定是否进行控制器重构，这样，既大大节约了生产时间和成本，也提高了控制效率。将该控制策略应用到连续搅拌反应釜系统中，取得了显著的应用成效。

关键词：分段仿射模型；显式模型预测控制；形式验证；连续搅拌反应釜；动态仿真

2015-12-07收到初稿，2015-12-17收到修改稿。

联系人及第一作者：王宇红（1970—），男，博士研究生，教授。

引 言

化工装置往往具有非线性特性和混杂特性，分段仿射（PWA）模型能够很好地描述这类装置的特性[1]。化工生产对控制实时性要求较高，能否准确及时地对生产过程进行控制，将直接影响生产的效率和产品的质量。目前，采用传统的模型预测控制技术[2-4]、非线性预测控制技术[5-6]、自适应控制技术[7-8]，均需要在线求取控制器，导致控制实时性不强。显式模型预测控制[9-10]分为离线计算和在线计算两部分，它通过离线计算得到系统状态和最优控制输入的显式关系，在线计算时，只需根据系统当前时刻状态，进行简单的线性运算，即可得到系统输入，从而大大减少了在线计算量，节省了在线计算时间，若采用显式模型预测控制技术对化工系统进行控制，则能够很好地满足化工生产对控制实时性的要求。

在实际化工生产过程中，也常常会出现一些异常或不理想的工作点，它们组成的集合称为危险状态集，为了使系统运行状态能够避开危险状态集，往往需要重新设计控制器以满足新的控制要求，这会导致控制的实时性变差，浪费大量生产时间，增加生产成本。如果先对系统进行形式验证[11-12]，即系统在给定时间内，在当前控制器的作用下，判断初始状态集中的状态，是否可达不安全状态集，根据判断的结果，再决定是否需要重新设计控制器，这样可以大大减少控制器重构的次数，从而提高了生产效率。

本文首先介绍了PWA模型，然后分别对基于PWA模型的显式模型预测控制算法和形式验证进行了详细的研究，最后提出了一种基于PWA模型的控制策略，并将该控制策略应用到连续搅拌反应釜（CSTR）系统中，达到了期望的控制效果。

1 PWA模型

PWA模型的特点是包含有限个连续变量动态子模型，随着系统状态的不断演化，系统根据切换律在不同模态之间进行切换，其表达式为[13-14]

2 基于PWA模型的显式模型预测控制

显式模型预测控制分为离线计算和在线计算两部分，它的基本思想是将模型预测控制算法与多参数规划理论相结合，通过离线计算求取显式控制律，那么在线计算过程就不需要复杂的优化计算，控制的实时性高。

2.1 离线计算

考虑如下控制问题：

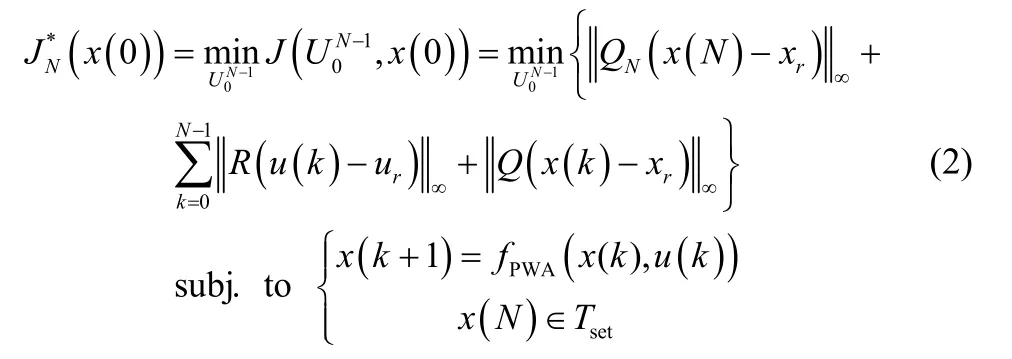
setN是权值矩阵，它们是满秩矩阵。这是带约束的有限时域最优控制问题，本文采用一种将动态规划理论与多参数线性规划理论相结合的方法求解该问题。

根据贝尔曼最优化原理，问题（2）可以表示为一个等价的动态规划问题[15-16]

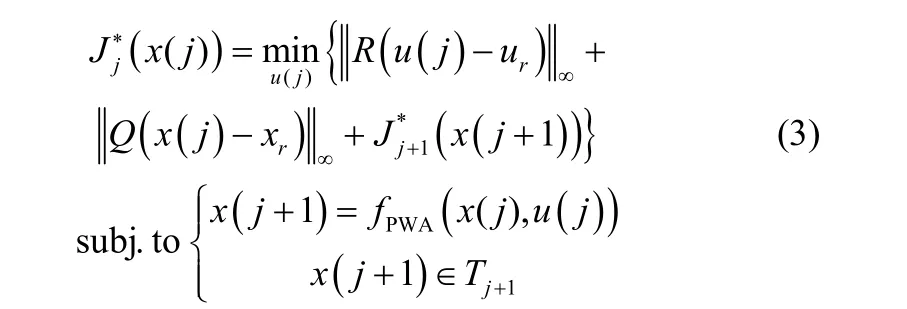
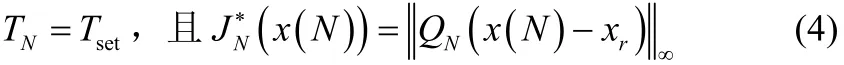
其中

是使问题（3）可行的所有状态的集合。

对于动态规划问题（3）、（4），若采用逆序解法求解，每一次迭代都可以将其转化为如下形式

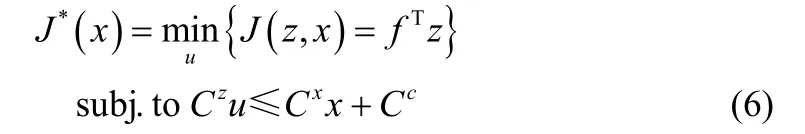
如果把x看作参数变量，u看作决策变量，那么式（6）可以看作多参数线性规划问题，通过求解该问题，得到分段仿射形式的显式控制率[15]

2.2 在线计算

在线计算过程只需检测系统当前时刻状态，先确定该状态所属的控制器分区，这实质上是一个“点定位”问题，采用文献[17]的方法，能够高效地解决该问题；再根据与该状态所属分区相对应的控制率子函数，即可求得系统输入，下一时刻，重复上述在线过程即可。

3 基于PWA模型的形式验证

对系统进行形式验证，本质是检验系统特定的行为属性是否满足控制要求。本文采用基于模型验证的方法，其中，系统模型为PWA模型，系统可能的输入通过显式模型预测控制器直接得到，形式验证算法如下所述。

（1）建立系统的形式验证模型

已知系统的PWA模型如式（1）所示，显式控制率如式（7）所示，依次求取与的交集为，得到系统的形式验证模型

可以看出，该形式验证模型为自治的PWA模型。（2）求取可达集定义1 对于自治系统其中，和均为多面体集，定义系统的一步可达集为。

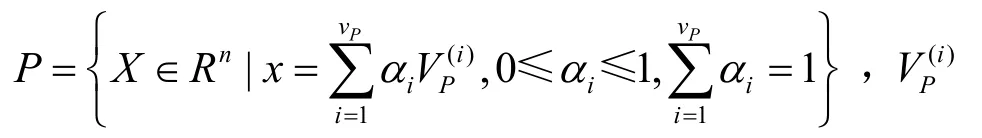
代表P的第i个顶点，vP代表P的顶点总数。

假设X0为满足系统状态约束条件的初始状态集，它是凸多面体集，根据建立的形式验证模型，求取与X0的交集为， h=1,… , q。如果将交集χh，h=1,… , q分别用它的顶点组合表示，其中，代表的第i个顶点，代表的顶点总数；那么，系统的一步可达集为其中，。根据递推关系，系统的N步可达集可通过，得到。

（3）给出验证结果

假设系统不安全状态集为Xf，要验证系统在有限步长N≤ Nmax内，是否可达Xf，其实只需要验证与是否有交集，当说明系统可达不安全状态集Xf，否则，不可达。

将基于PWA模型的显式模型预测控制与形式验证相结合，即可得到全新的控制策略：建立系统的PWA模型，采用显式模型预测控制算法对系统进行控制，针对系统在实际运行过程中出现危险状态集的情况，先对系统进行形式验证，再决定是否需要重新设计控制器，以期最终达到控制目标。

4 仿真实例

4.1 CSTR系统的PWA模型

CSTR是化工生产过程中必不可少的生产工具，由于它具有高度非线性、多变量和多工作点的特点，采用简单单一的模型往往不能很好地反映系统的特性，这里采用PWA模型对其进行建模，一个标准两状态的CSTR系统如图1所示。

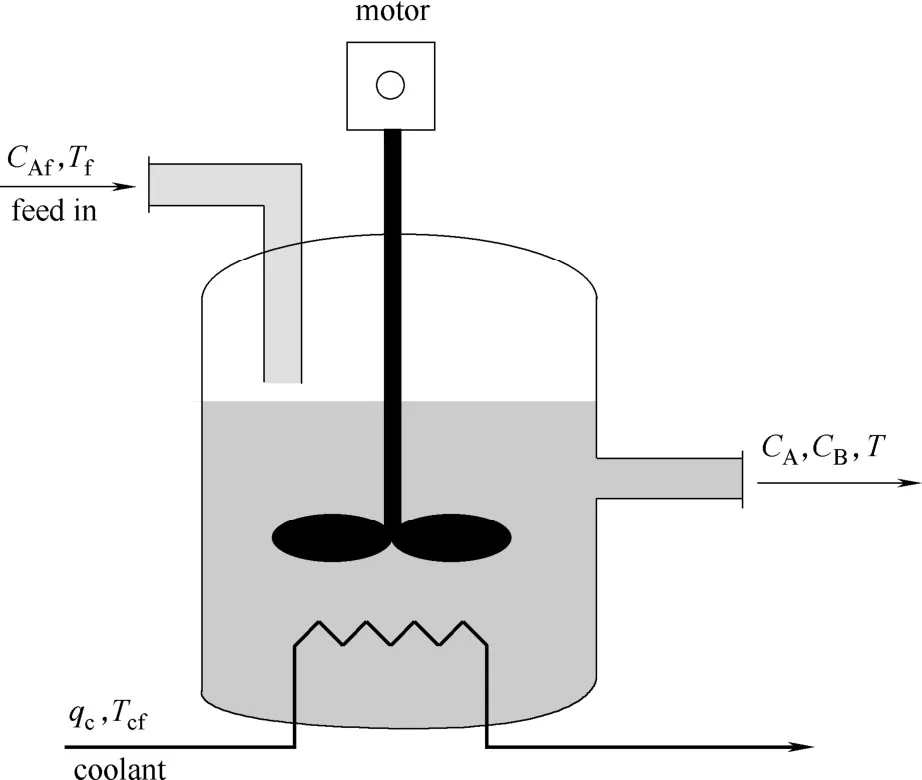
图1 连续搅拌反应釜Fig.1 Continuous stirred tank reactor

假设反应釜中发生的化学反应为不可逆放热反应A→ B，其中，CA为产物浓度，T为反应釜内温度，qc为冷却剂流量，Tcf为冷却剂温度。根据文献[18-19]，令CA和T分别为系统的状态变量x1, x2； Tcf为系统的输入u；CB为系统的输出y，则CSTR系统可由式（8）描述

其中κ(x2)λ=20.0，x1f= 1.0，，变量的取值范围为。

在额定工作条件下，系统有3个稳定工作点：xs1=(0.856,0.886)，xs2=(0.5528,2.7517)，xs3= (0.2353,4.7050)，其中，xs1, xs 3为渐近稳定工作点，xs2为局部稳定工作点。

若在稳定工作点处先对式（8）进行线性化，再离散化，即可建立CSTR系统的PWA模型为

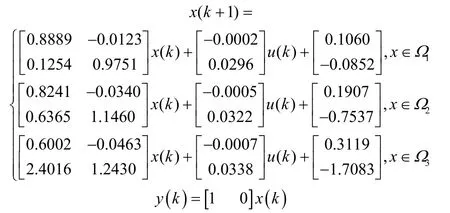
4.2 仿真结果与分析

化工生产过程中，CSTR系统需要工作在不同的工作点（稳态点）处，以便生产出所需要的产品，这里假设某一产品在点处产出，系统初始状态集为控制目标是使X0中的状态点，在输入作用下，都能够达到期望的工作点xs1处。若选取任意一个符合要求的状态点x0=( 0.35,0.4 )作为系统初始状态，应用上述控制策略进行仿真，仿真结果如图2～图4所示。

图2 显式模型预测控制器状态分区Fig.2 Partitions of explicit model predictive controller

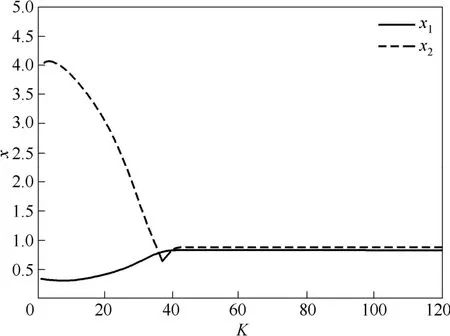
图3 CSTR系统的状态演化曲线Fig.3 State evolution of CSTR system

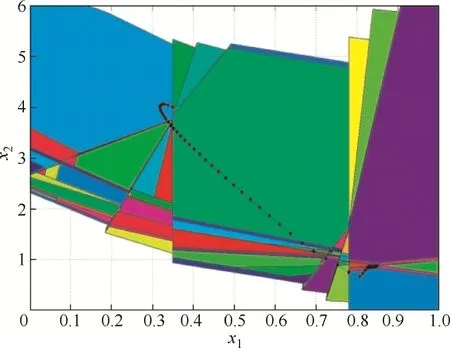
图4 CSTR系统状态演化过程的相平面图Fig.4 Phase-plane diagram of state evolution of CSTR system

图2中，显式模型预测控制器共有26个不同的子控制率分布在162个状态分区上，其中，不同颜色的分区对应不同的子控制率。图3中，在K =42时，系统达到并稳定在期望的工作状态，整个控制过程快速平稳。图4反映系统状态在状态空间演化过程及在不同采样时间经过的控制器分区。

在产品生产过程中，若检测到危险状态集时，假设两种情况

其中Xf1和Xf2代表危险状态集。

先对系统进行形式验证，在当前控制器作用下，如果系统初始状态集中所有状态不可达危险状态集，则不需要重构控制器；反之，则需要重构控制器。根据形式验证算法，得到验证结果如图5～图6所示。

图5～图6中，绿色区域代表初始状态集，红色区域代表危险状态集，蓝色区域代表可达集。图5中，系统初始状态集中的状态不可达危险状态集，所以针对情况一，不需要对控制器进行重构。图6中，系统初始状态集中的状态可达危险状态集，所以针对情况二，需要应用显式模型预测控制算法，重新设计满足要求的控制器，仿真结果如图7～图8所示。

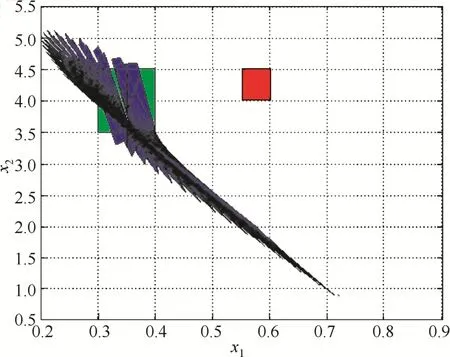
图5 CSTR系统的形式验证（情况一）Fig.5 Formal verification of CSTR system (Situation 1)

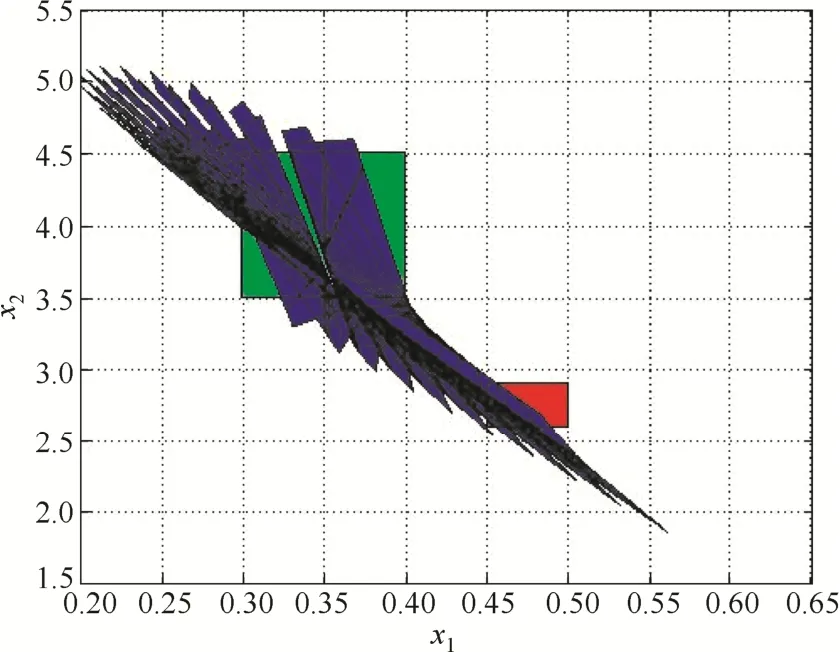
图6 CSTR系统的形式验证（情况二）Fig.6 Formal verification of CSTR system (Situation 2)

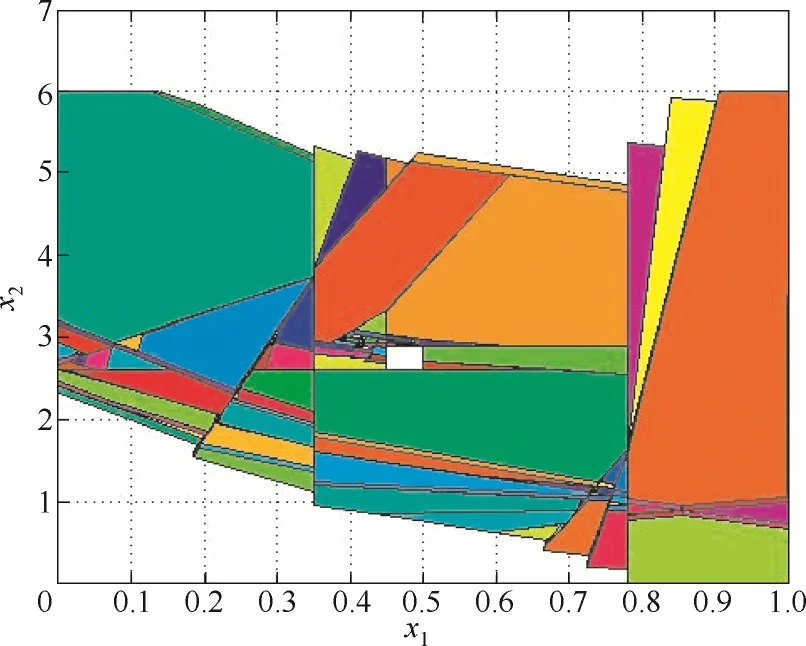
图7 重构后的显式模型预测控制器状态分区Fig.7 Partitions of controller after reconfiguration

图7中，新的显式模型预测控制器共有43个不同的子控制率分布在320个状态分区上。图8中，在新的控制器作用下，系统仍然能够从初始状态x0达到期望的工作状态，整个控制过程快速平稳且避开了不安全状态。

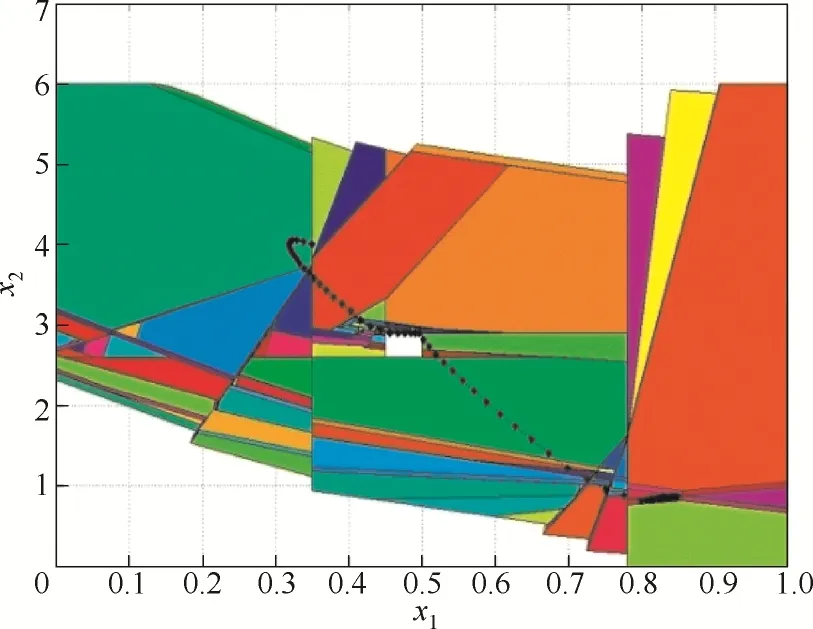
图8 重构后系统状态演化过程的相平面图Fig.8 Phase-plane diagram of state evolution under new controller

由于模型预测控制方法[20-21]在化工生产中有较为广泛的应用，为了说明本文控制策略的高效性，与传统的模型预测控制方法进行比较。仍然在上述条件下，仿真结果表明，采用传统的模型预测控制方法，在K =68时，系统从初始状态到达期望工作状态，平均完成一次在线过程的时间为3320 ms，当出现危险状态集时，均需要重新设计控制器；而采用本文控制策略，在K =42时，系统从初始状态到达期望工作状态，平均完成一次在线过程的时间为2.1 ms，当出现危险状态集时，控制器重构的次数仅为1次。可以看出，本文控制策略在控制的实时性、所需的计算量和计算时间方面均优于传统的模型预测控制方法。

5 结 论

本文阐述了一种基于PWA模型的控制策略，并将其应用到CSTR系统中进行仿真研究。仿真结果表明，PWA模型很好地反应了CSTR系统的特性，显式模型预测控制可以使CSTR系统状态快速平稳地达到期望的状态（如稳定的工作点），在运行过程中，检测到危险状态集出现时，先对系统进行形式验证，再决定是否需要对控制器进行重构。情况一不需要进行控制器重构，继续使用当前控制器即可满足控制要求；情况二则需要进行控制器重构，将重构后的控制器作用于系统，可以看出系统状态演变过程避开了不安全状态，满足了新的控制要求。最后，与传统的模型预测控制方法进行比较，说明了该控制策略的高效性。

References

[1] GARULLI A, PAOLETTI S, VICINO A. Survey on switched and piecewise affine system identification [C]//Proc. 16th IFAC Symposium on System Identification. Holland: Elsevier, 2012: 344-355.

[2] QIN S J, BADGWELL T A. A survey of industrial model predictive control technology [J]. Control Engineering Practice, 2003, 11 (7): 733-764.

[3] KUMAR S A, AHMAD Z. Model predictive control (MPC) and its current issues in chemical engineering [J]. Chemical Engineering Communications, 2012, 199 (4): 472-511.

[4] LEE J H. Model predictive control: review of the three decades of development [J]. International Journal of Control, Automation and Systems, 2011, 9 (3): 415-424.

[5] 钱积新. 非线性预测控制 [M]. 北京: 科学出版社, 2015: 83-150.

QIAN J X. Nonlinear Predictive Control [M]. Beijing: Science Press, 2015: 83-150.

[6] 杨剑锋, 赵均, 钱积新,等. 一类化工过程多变量系统的自适应非线性预测控制 [J]. 化工学报, 2008, 59 (4): 934-940. DOI:10.3321/ j.issn:0438-1157.2008. 04.021.

YANG J F, ZHAO J, QIAN J X, et al. Adaptive nonlinear model predictive control for a class of multivariable chemical processes [J]. Journal of Chemical Industry and Engineering (China), 2008, 59(4): 934-940. DOI:10.3321/j.issn:0438-1157.2008.04.021.

[7] 韩正之. 自适应控制 [M]. 北京：清华大学出版社, 2014.

HAN Z Z. Adaptive Control [M]. Beijing: Tsinghua University Press, 2014.

[8] 王东, 周东华, 金以慧. 自适应广义一般模型控制 [J]. 化工学报, 2003, 54 (3): 344-349. DOI: 10.3321/ j.issn:0438-1157.2003.03.016

WANG D, ZHOU D H, JIN Y H. Adaptive generalized generic model control [J]. Journal of Chemical Industry and Engineering (China), 2003, 54 (3): 344-349. DOI:10.3321/j.issn:0438-1157.2003.03.016.

[9] MAGNI L, RAIMONDO D M, ALLGÖWER F. Nonlinear Model Predictive Control: Towards New Challenging Applications [M]. Berlin: Springer-Verlag, 2009.

[10] OBERDIECK R, PISTIKOPOULOS E N. Explicit hybrid model predictive control: the exact solution [J]. Automatica, 2015, 58 (8): 152-159.

[11] IMMLER F. Verified Reachability Analysis of Continuous Systems [M]. Berlin: Springer Berlin Heidelberg, 2015: 37-51.

[12] FANG M, ZHANG Y S, HUI L I. Formal verification of hybrid systems [J]. Journal of System Simulation, 2006, 18 (10): 2921-2920.

[13] HEEMELS W P M, SCHUTTER B D, BEMPORAD A. Equivalence of hybrid dynamical models [J]. Automatica, 2001, 37 (7): 1085-1091.

[14] TORRISI F D, BEMPORAD A. HYSDEL—a tool for generating computational hybrid models for analysis and synthesis problems [J]. IEEE Transactions on Control Systems Technology, 2004, 12 (2): 235-249.

[15] BAOTIĆ M, CHRISTOPHERSEN F J, MORARI M. A new algorithm for constrained finite time optimal control of hybrid systems with a linear performance index[C]// Proc. Europe Control Conference. Piscataway: IEEE, 2003: 3335-3340.

[16] BERTSEKAS D P. Dynamic Programming and Optimal Control [M]. Massachusetts: Athena Scientific, 1996.

[17] CHRISTOPHERSEN F J, KVASNICA M, JONES C N, et al. Optimal Control of Constrained Piecewise Affine Systems [M]. Berlin: Springer Berlin Heidelberg, 2007: 150-165.

[18] DU J J, SONG C Y, LI P. Modeling and control of a continuous stirred tank reactor based on a mixed logical dynamical model [J]. Chinese Journal of Chemical Engineering, 2007, 15 (4): 533-538.

[19] ÖZKAN L, KOTHARE M V, GEORGAKIS C. Control of a solution copolymerization reactor using multi-model predictive control [J]. Chem. Eng. Sci., 2003, 58 (7): 1207-1221.

[20] 张端, 高岩, 章苗根,等. 线性规划实现动态优化的模型预测控制策略 [J]. 化工学报, 2010, 61 (8): 2121-2126.

ZHANG D, GAO Y, ZHANG M G, et al. Model predictive control strategies to realize dynamic optimization based on linear programming [J]. CIESC Journal, 2010, 61 (8): 2121-2126.

[21] 李秀改, 高东杰, 王宇红. 基于混合逻辑动态模型的混杂系统预测控制 [J]. 控制与决策, 2002, 3 (3): 315-319.

LI X G, GAO D J, WANG Y H. Predictive control for hybrid system based on mixed logic dynamic model [J]. Control and Decision, 2002, 3 (3): 315-319.

研究论文

Received date: 2015-12-07.

Foundation item: supported by the Natural Science Foundation of Shandong Province (2013ZRE28089).

Application of a control strategy based on PWA model in CSTR system

WANG Yuhong, YANG Pu
(College of Information and Control Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China)

Abstract:There will be some abnormal working states in the process of chemical production, so the controller of the system often needs to be reconfigured in order to keep the system running normally. In view of this situation, a control strategy based on piecewise affine (PWA) model is proposed. In the strategy, a system is modeled in PWA form and an explicit model predictive control algorithm is applied to control the system. When abnormal operating points are detected, formal verification is first used to decide whether the controller needs to be reconfigured or not. By this way, it not only saves production time, but also improves the control efficiency. An application case study on CSTR system is given to illustrate the effectiveness of this strategy.

Key words:PWA model; explicit model predictive control; formal verification; CSTR; dynamic simulation

DOI：10.11949/j.issn.0438-1157.20151844

中图分类号：TP 273

文献标志码：A

文章编号：0438—1157（2016）03—0865—06

基金项目：山东省自然科学基金项目（2013ZRE28089）。

Corresponding author:Prof. WANG Yuhong, y.h.wang@upc.edu.cn