不确定环境下自动化集装箱码头AGV调度与配置问题

马越汇,胡志华

(上海海事大学物流研究中心， 上海201306)



不确定环境下自动化集装箱码头AGV调度与配置问题

马越汇,胡志华

(上海海事大学物流研究中心， 上海201306)

摘要：为研究不确定环境下自动化集装箱码头AGV调度与配置问题，建立了以最末任务结束时间最小化为目标的基本模型，将装卸集装箱任务的带箱作业时间，完成一个任务后到执行下一个任务之前空箱行驶的时间这两个决策变量在合理的范围内生成了5 000个数据，选取其中有代表性的数据进行分析。考虑了不确定因素,例如集装箱码头堆场内的交通控制、交通拥堵情况等。结果表明：外界不确定因素对于最末任务结束时间最小值的影响是有限的，在一定程度上增加了工作时间，但不是时间增加的决定性因素；自动化集装箱码头实际运行过程中，并不是AGV数量越多，整个运作效率就会越高；随着AGV数量增加时，外界不确定因素对最末任务结束时间最小值的影响就会越来越小，直到几乎没有影响。算例证明了模型的有效性和实用性。

关键词：自动化集装箱码头；自动引导车；随机规划模型；调度与配置

0引言

AGV(automated guided vehicle)，指装备有电磁或光学等自动导引装置，能够沿规定的导引路径行驶，具有安全保护以及各种移载功能的运输车，工业应用中不需要驾驶员的搬运车，可充电的蓄电池为其动力来源。集装箱运输作为国际货物运输物流系统的一个重要节点,集装箱运输效率的高低会直接影响经济的发展，由于AGV具有自动化、智能化、并行作业的特点，能够很好地满足自动化集装箱码头的运输要求，因此在自动化集装箱码头得到了广泛的应用。

在集装箱卸船作业中，首先码头为船舶分配泊位，岸吊将集装箱放置在AGV上，AGV按照规定路径将集装箱运载至指定箱区，再由龙门吊将集装箱卸载至指定箱区的指定位置。集装箱装船作业的顺序与卸船作业相反。一般可通过电脑来控制AGV的行进路线以及行为，或利用电磁轨道来设立其行进路线，电磁轨道粘贴在地板上，AGV依循电磁轨道所带来的信息进行移动与动作。

Lee等[1]考虑了在集卡资源限制下的调度模型，建立了以集卡等待时间和运输时间加权和最小为目标函数的模型，设计了新的混合算法来求解模型。Cao等[2]针对集装箱码头在堆场卡车和堆场桥吊的装载作业的调度问题，建立了混合整数规划模型。Elmekkawy等[3]针对自动化集装箱码头研究了一种新的方法，结合了遗传算法开发了一种MA算法，提高AGV系统工作效率。Giuseppe等[4]将AGV的调度问题转化成最小流问题，并且建立了最小流模型，使用了贪婪算法和单纯形算法进行求解，将结果进行对比。康志敏[5]阐述了两种不同的AGV调度方式，提出了基于成本的AGV路线调度方法，在作业面动态调度模型下，建立了等待时间最少为目标的车辆调度模型，利用遗传算法来求解。徐远琴等[6]考虑了集卡运输时间与等待岸桥、场桥时间之间的权重系数，建立了以等待岸桥、场桥作业时间与集卡运输时间之和最小为目标的联合调度优化模型。张远春等[7]以生产线产能最大化为目标,以生产工艺、AGV路径、调度规则等为约束条件,建立了以AGV的数量为决策变量的数学模型，利用仿真得到优化方法。计明军等[8]提出了集卡与岸桥协同调度模型，并设计了进化规划算法求解该模型，以达到任务完成时间最少的目标。曾庆成等[9]考虑了等待时间问题，提出了综合考虑岸桥和场桥等待集卡的时间最小的集卡调度方法，采用Q-学习法对模型进行求解。秦天保等[10]以完工时间最小为目标，构建带有任务顺序约束的岸桥与集卡集成调度的 MIP 模型和约束规划模型。马超等[11]针对集装箱码头岸桥和集卡的协同调度问题，以进口箱和出口箱的总完工时间最短为目的，考虑了集卡路径约束和岸桥实际操作情况等实际约束，构建了边装边卸的混合整数规划模型。梁承姬等[12]针对集装箱码头集卡调度问题，建立基于岸桥作业并考虑时间窗约束的集卡协调调度耦合模型，目的为使集卡数最小且延误时间最短。

已有的文献中几乎都忽略自动化集装箱码头实际作业中不确定因素的，例如集装箱运输过程中堆场交通拥堵情况, 并且所建立的模型假设条件太多,与自动化集装箱码头实际作业相差不少,调度模型的研究也仅仅局限在理论层面,很难有实际意义。本文的创新之处就在于将这些不确定性因素考虑进去，使得模型更具现实意义。

本文首先结合AGV、岸桥、堆场、龙门吊四者建立了最末任务结束时间最小化为目标函数的模型。其次设计了算法来计算AGV任务作业完成时间、两个任务之间的空箱行驶时间。因为考虑到实际运行过程中，自动化集装箱码头不确定性因素，不确定因素包括堆场内的交通控制、交通拥堵情况等，因此在合理范围内对前述两个时间生成5 000组数据。采用数学建模和数据分析的方法研究AGV的调度问题，AGV一定时，最末任务结束时间是否受不确定因素影响；任务一定时，AGV的数量与最末任务结束时间、不确定性因素的关系,最后通过算例验证了模型的有效性和实用性。

1模型建立

图1为一个自动化集装箱码头的俯视图，共有5岸桥，6个箱区，每辆AGV按图1中所示箭头规定路径进行运作，在集装箱卸船作业中，首先码头为船舶分配泊位，岸吊将集装箱放置在AGV上，AGV按照规定路径将集装箱运载至箱区，再由龙门吊将集装箱卸载至所需要存放箱区的位置。集装箱装船作业的顺序与卸船作业相反。AGV的作业轨迹跟装船作业与卸船作业有关，根据集装箱卸下的位置和装载的位置确定其路径。本文使用参数1计算装卸集装箱任务的带箱作业时间为Ti，使用参数2计算在完成一个任务后到执行下一个任务之前空箱行驶的时间为Tij。

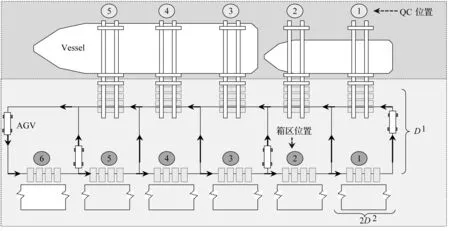
图1　自动化集装箱码头的俯视图示例

1.1符号

本文建立AGV的装卸作业任务调度模型，相关符号的定义如下：

I:N项任务的集合,I={1,2,…,N}，其中1和N表示起止两个虚拟任务；

V: AGV的集合,V={1,2,…,|V|}；

k:k=∑ijTij+∑iiTi，一个足够大的数；

Tij: 在完成任务i(i∈I)后去执行任务j,(j∈I)AGV空箱行驶的时间；

xijv:xijv∈{0,1},若v∈V在完成任务i∈I后执行下一个任务j∈I,则xijv为1; 否则xijv为 0；

yiv:yiv∈{0,1}，如果车辆v∈V执行任务i∈I，则yiv为1;否则yiv为0；

zi: 任务i∈I工作的开始时间；

f: 所有工作的完工时间，即最后一个任务完成时的时间；

Rv: AGV,v∈V最早有效使用的时间；

Ti: 任务i∈I的工作时间；

Ai: 任务i∈I的最早有效开始工作时间。

1.2基本模型

自动化集装箱码头AGV的调度问题，以最小化最末任务结束时间为目标建立模型，模型的目标函数与约束条件如下：

minf,

(1)

s.t.f≥zi+Ti,∀i∈I,

(2)

zj+(1-xijv)K≥zi+Ti+Tij,∀i≠j,v∈V,

(3)

zi≥Ai,∀i∈I,

(4)

Zi≥Ri+T1,i+(yi,v-1)K,∀i∈I,v∈V,

(5)

∑j∈I+{i}xjiv=∑j∈I+{i}xijv=yiv,∀i∈I,v∈V,

(6)

∑vyiv=1,∀i∈I,

(7)

xijv+xjiv≤1,∀i,j∈I,i≠j,v∈V,

(8)

∑i∈I+{1}x1,i,v=1,∀v∈V,

(9)

∑i∈I+{N}xi,N,v=1,∀v∈V,

(10)

f≥0,zi≥0,∀i∈I,

(11)

式(2)是最末任务结束时间的最小值f；式(3)表示f是由每个任务的开始工作时间和完成任务的时间决定的；在分配每辆AGV的任务顺序时，需要考虑每个任务的开始时间，以免任务分配发生时间重叠；式(4)对任意AGV (v)安排的作业任务序列，如果完成任务i后又执行任务j，则xijv=1，那么要求满足zi≥zi+Tij+T，即zi≥xijv(zi+Tij+T);式(5)表示任务i∈I的开始时间在其可执行的最早开始时间后进行；式(6)表示车辆v∈V所要完成的任务i∈I在AGV的有效工作时间内进行；式(7)对任意AGV，对任意非虚拟任务，满足该任务在任务网络中的流约束；式(8)每个任务只可以由一辆AGV完成运输;式(9)对于任意AGV，从虚拟任务出发，到虚拟任务完成运输，仅负责一个作业流程;式(10)和式(11)对于每辆AGV都是从虚拟任务开始，到虚拟任务后结束。

2参数估计

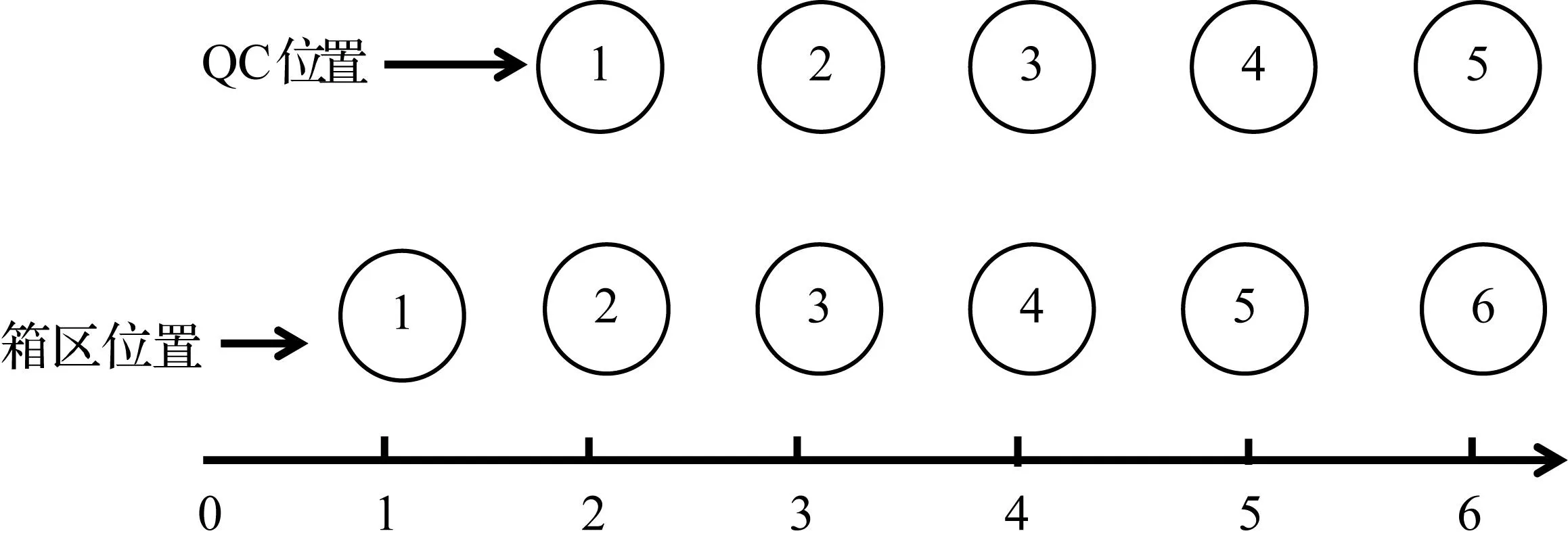
图2　岸桥与箱区的位置坐标

Lui,Luj:i∈I,j∈I，若Lui,Luj为1是卸船任务；否则是装船任务；

S: AGV的行驶速度；

Lu1: 岸桥装载和卸载一个集装箱的时间；

Lu2: 龙门吊装载和卸载一个集装箱的时间；

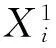
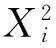
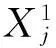
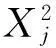
Di: 装卸集装箱任务i的带箱行驶距离;

Dij: 完成任务装卸作业i后去执行任务j之前空箱行驶距离。

①参数估计1：装卸集装箱任务i的带箱行驶时间。

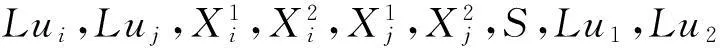
输出:Di,Ti

步骤:

Step 1: 根据Lui,Luj计算距离Di,若Lui,Luj=1,则转step 2;否则转step 3;

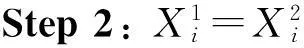
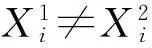
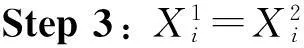
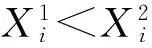
Step 4: 根据距离Di,计算时间Ti=Di/S+Lu1+Lu2。

②参数估计2：AGV完成一个任务i后到执行下一个任务j之前空箱行驶的时间。

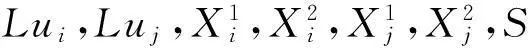
输出:Dij,Tij

步骤:

Step 1: 根据Lui,Luj,i∈I,j∈J的值计算距离Dij,

如果Lui=1,Luj=1,转step 2,

如果Lui=0,Luj=0,转step 3,

如果Lui=0,Luj=1,转step 4,

如果Lui=1,Luj=0,转step 5;

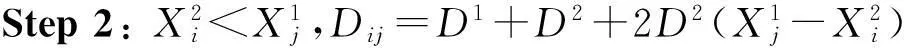
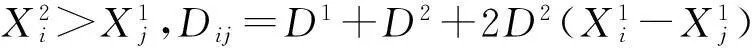
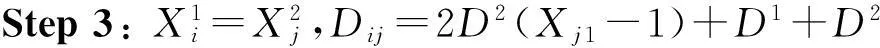
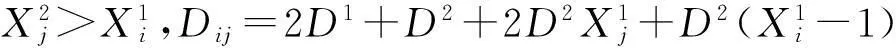
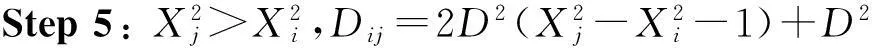
Step 6:Tij=Dij/S。

3算例

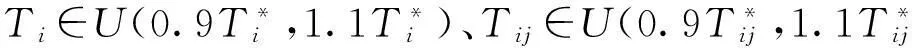
本文对AGV=2、3、4、5、6、7、8情况下的最末任务结束时间最小值的5 000组数据分别画出正态概率分布图，发现图形的增长趋势类似，以y=20.369ln(x)+402.08为例，画出柱状图和拟合图，见图3。对每组数据最大值与最小值的差值进行比较，当AGV数量很少时，差值还是很大的，随着AGV数量的增多，每组数据的最大值与最小值的差值就越来越小，说明在AGV数量很少时，外界不确定因素对最末任务结束时间最小值影响很大；随着AGV数量增加时，外界不确定因素对最末任务结束时间最小值的影响就会越来越小，直到几乎没有影响，见图4和图5。

对8种情况下5 000组数据最大值，平均值和最小值散点进行了拟合，因为图形类似，于是以一种情况为例画拟合图，见图6。发现最大值、平均值和最小值的拟合程度很高，最大值的拟合线为y=-24.546x+541.9，存在明显的负相关线性关系。本文可以这样理解，在自动化集装箱码头中实际运输过程，最末任务完成时间最小值总受不确定因素影响，所有最末任务结束时间最小值当中，最大值变化是很明显的，这就意味着最末任务结束时间最大值受外界不确定性因素影响是很大的，呈负相关关系；所有最末任务结束时间最小值当中，最小值变化幅度不大，最小值的拟合直线为y=432.29x-0.155，趋向于一个平缓趋势。说明，外界不确定因素对于最末任务结束时间最小值的影响是有限的，在一定程度上增加了工作时间，但不是时间增加的决定性因素。

本文考虑Tasks为10和20，AGV=2,3,4,5, 6,7,8时，对应的f值，得到了5 000组解，为了使得结果清晰明了，本文对每一组Tasks随机选取了7组数据(表1)绘制折线图。

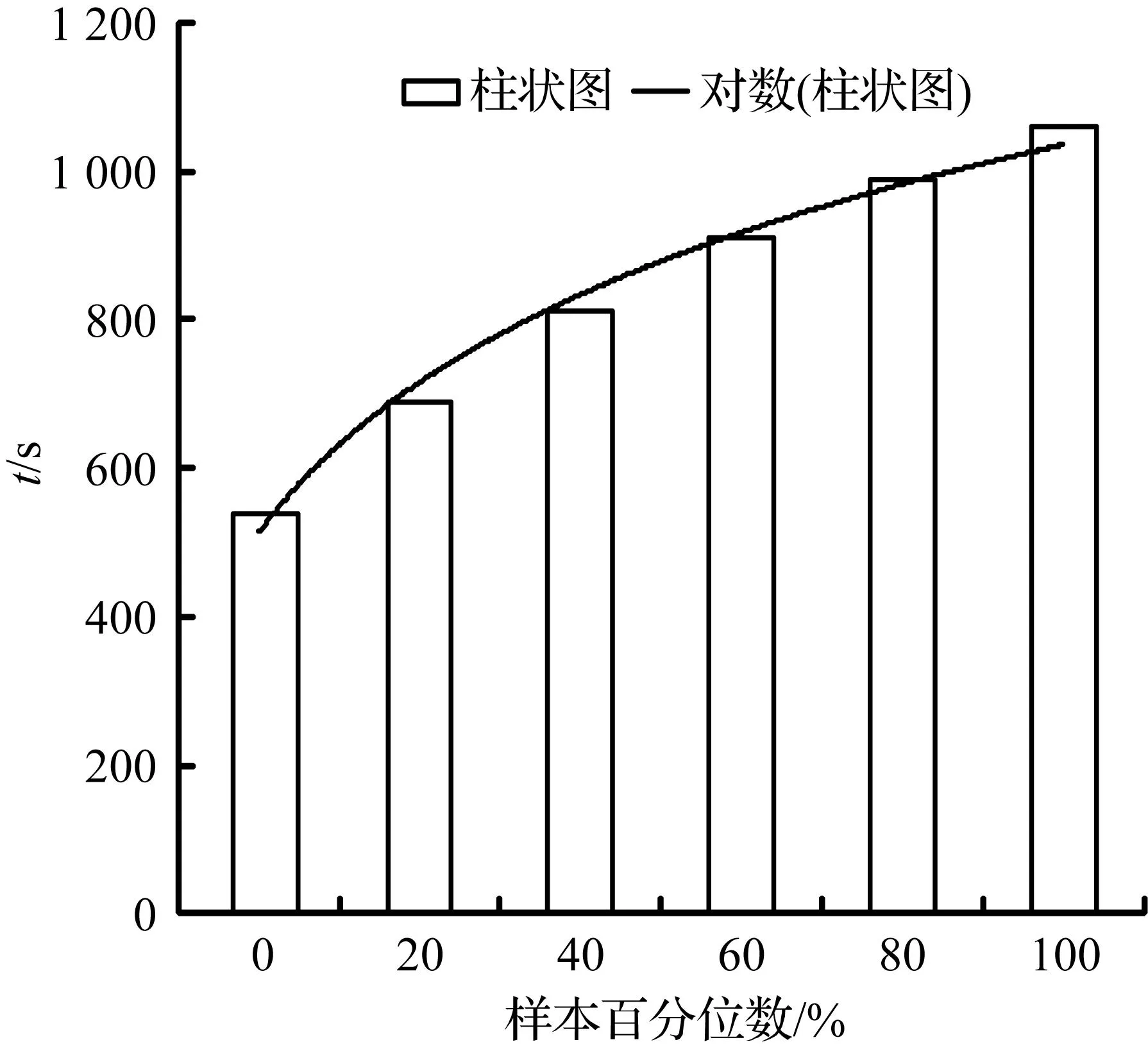
图3最末任务结束时间最小值的正态概率分布图

Fig.3Normal probability distribution of

the minimum last task end time

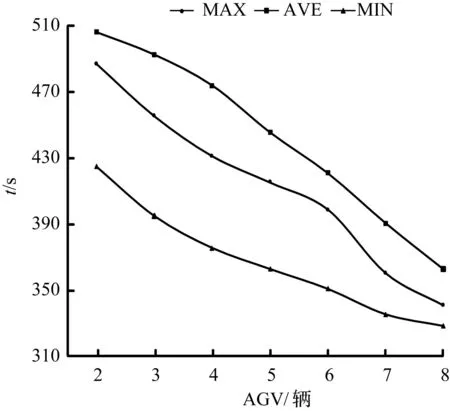
图4最末任务结束时间最大值、平均值

最小值随AGV数量的变化

Fig.4The maximum、average、minimum of the

last task end time values changes with AGVs

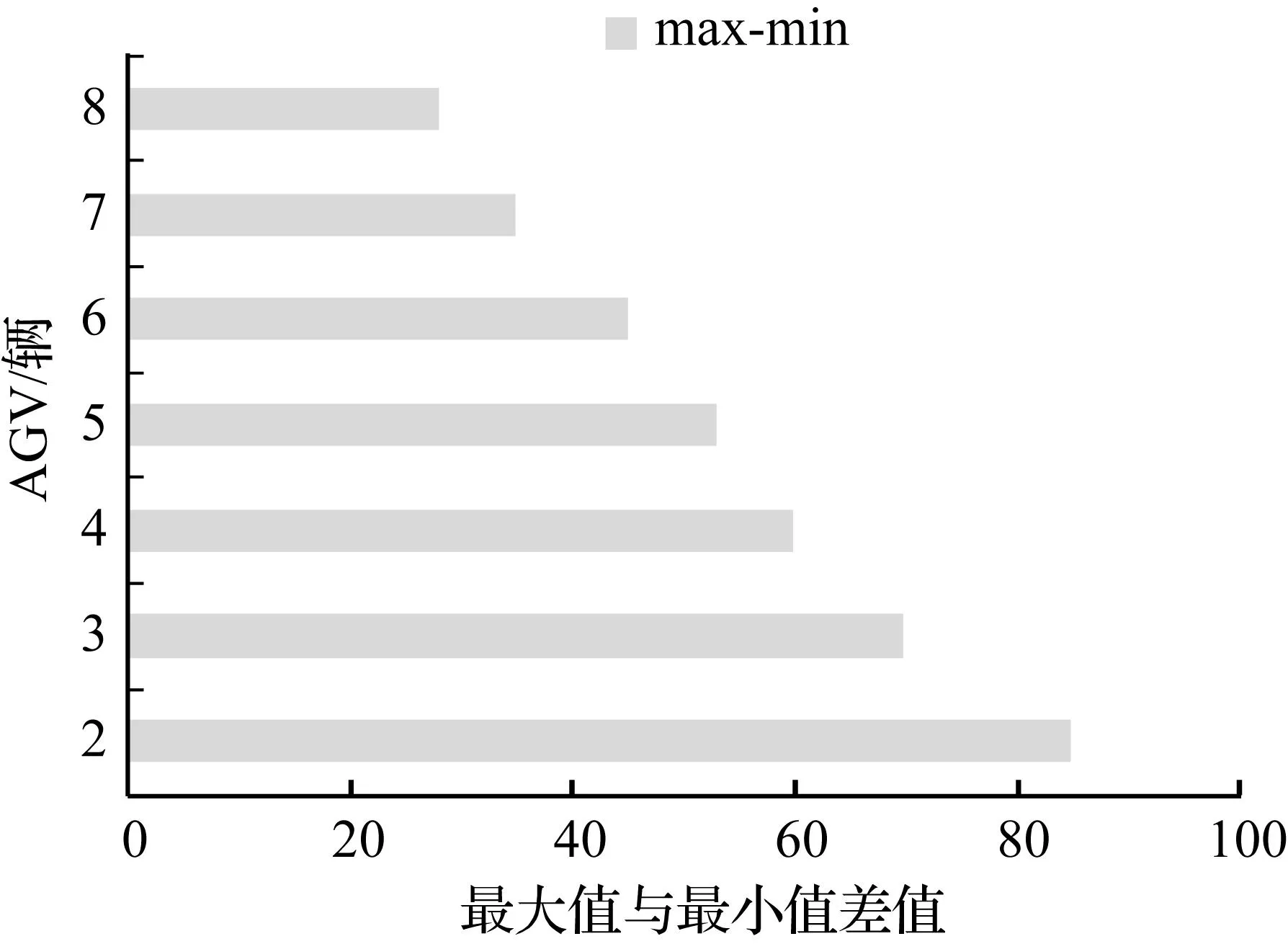
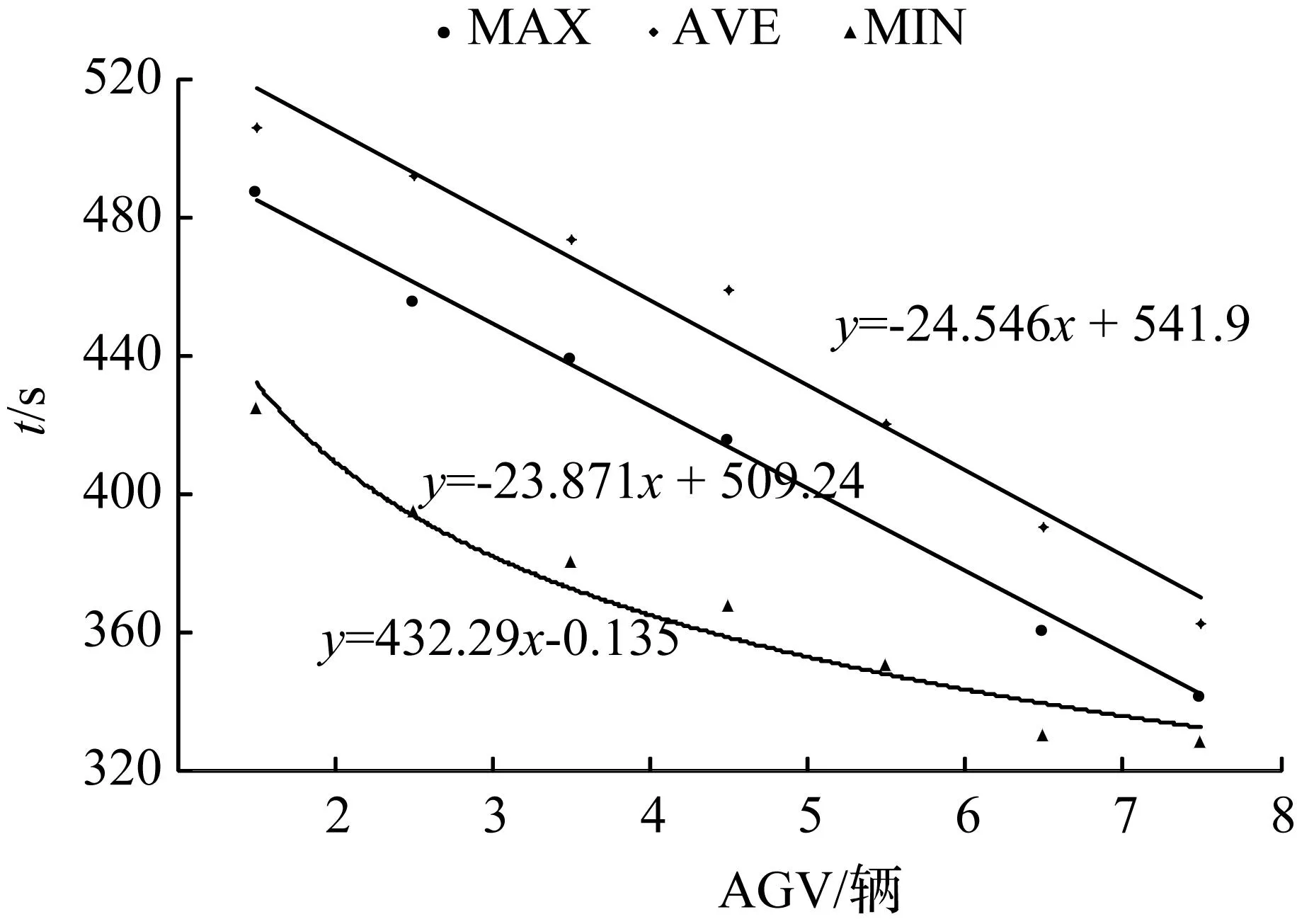
图5　最末任务结束时间最大值

首先，用对数趋势线对AGV最末任务结束时间最小值关系图进行拟合见图7和图8,发现拟合效果很好，见表2。当任务一定时，一开始曲线下降的速度很快，但之后降速又会趋于平稳。 随着AGV数量的增加，最末任务结束时间最小值基本上是呈下降的趋势，但是当数量趋于一定的值时，最末任务结束时间最小值就趋向于一个值，不会再发生明显的上升或者下降，也就是说在自动化集装箱码头实际运

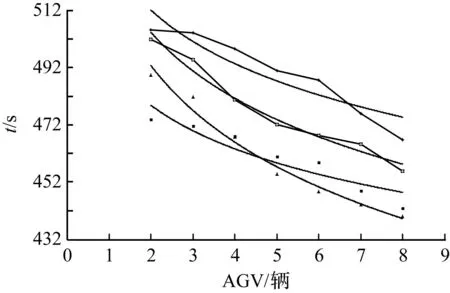
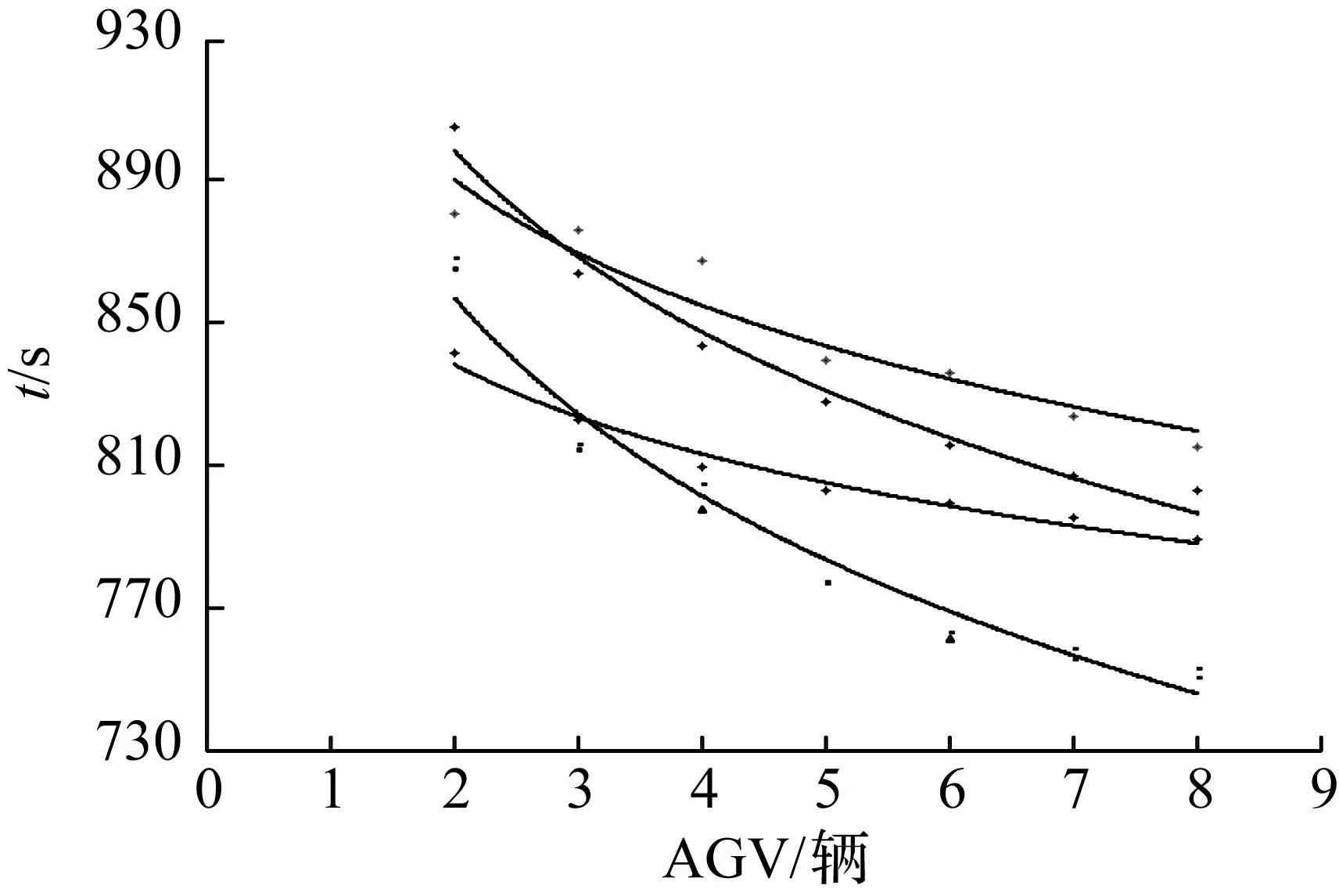
图7　AGV与最末任务结束时间最小值关系

行过程中，并不是AGV数量越多，整个运作效率就会越高，对于AGV的数量选择，码头工作人员应该选取一个相对最优值。

同时还可以看出，当任务一定时，最末任务结束时间最小值一定时，存在8辆AGV完成任务的时间与3、4辆AGV完成任务的时间相同的情形，说明外界不确定因素对自动化集装箱码头运输确实有影响，合理安排工作流程，对AGV进行合理调度，减少岸吊、龙门吊等待的时间都是很有必要的。

根据两次试验，自动化集装箱码头实际运行过程中，AGV的成本较高，需根据任务数目，选择合适的车辆数，车辆数目并不是越多越好，可以通过一定的方式，得出AGV的最优值，这样可以降低很多成本；其次,外界不确定因素对最末任务结束时间最小值确实是有影响的，但不是决定性因素，集装箱码头内部应该尽量安排好自己的作业流程，避免发生任务重叠，交通拥堵情况，提高工作效率，降低工作成本，增加码头的竞争力。

4结语

在自动化集装箱码头对于AGV的调度模式要科学与合理，合理的调度模式可以提高 AGV的利用率，减少空驶时间，提升重载率，并且其制造成本较高，如果使用效率太低的话，不仅会增加成本，造成资源浪费，而且会降低生产效率，影响企业的服务效率。本文在已有文献的基础上考虑了不确定因素，包括自动化集装箱码头堆场内的交通控制、交通拥堵情况等，建立了以最末任务结束时间最小化为目标的混合整数规划模型，研究了不确定环境下AGV的调度与配置问题，对今后研究该领域的问题提供理论价值，有实际应用价值。

不足之处就在于，没有考虑具体的某种不确定性因素对集装箱码头调度的影响，以及对AGV数量的影响，以后可以在这方面进行研究。

参考文献:

[1]LEE D , CAO J X, SHI Q X, et, al.Integrated quay crane and yard truck schedule problem in container terminals[J]. Tsinghua Science and Technology, 2010, 15(4): 467-474.

[2]CAO J X, LEE D H, CHEN J H, et, al.The integrated yard truck and yard crane scheduling problem: Benders’ decomposition-based methods[J]. Transportation Research Part E:Logistics and Transportation Review,2010, 46(3):344-353.

[3]ELMEKKAWY T Y, LIU S.A new memetic algorithm for optimizing the partitioning problem of tandem AGV systems[J]. International Journal of Production Economics, 2009, 118(2): 508-520.

[4]CONFESSORE G, FABIANO M, LIOTTA G.A network flow based heuristic approach for optimising AGV movements[J]. Journal of Intelligent Manufacturing , 2011, 24(2): 405-419.

[5]康志敏.集装箱自动化码头 AGV 路径优化和调度研究[D]. 武汉理工大学,2011.

[6]徐远琴，韩晓龙.集卡与岸桥及场桥联合调度模型优化[J],重庆交通大学学报(自然科学版),2013,32(2):318-320.

[7]张远春,范秀敏,驹田邦久.基于仿真优化的多种类型AGV数量配置优化方法[J]. 中国机械工程, 2011, 22(14):1680-1685.

[8]计明军，靳志宏.集装箱码头集卡与岸桥协调调度优化[J]. 复旦学报(自然科学版),2007,46(4):476-480.

[9]曾庆成.集装箱码头装卸作业集成调度模型与方法[D]. 大连：大连海事大学，2008.

[10]秦天保，彭嘉瑶，沙梅.带任务顺序约束的岸桥集卡集成调度约束规划模型[J]. 上海海事大学学报，2013,34(3):1-7.

[11]马超，梁承姬.集装箱码头岸桥分配与集卡调度整合问题研究[J]. 广西大学学报(自然科学版)，2015，40(3):643-650.

[12]梁承姬,王玲玲,佘文静.考虑时间窗约束的集卡调度耦合模型及求解[J]. 广西大学学报(自然科学版)，2014,39(3):656-662.

(责任编辑梁碧芬)

The dispatching and scheduling problems of AGVs at automated container terminals under uncertainty conditions

MA Yue-hui, HU Zhi-hua

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

Abstract：In order to study the dispatching and scheduling problems of AGVs at automated container terminals under uncertainty conditions, a model for minimizing the last task end time is established. 5000 data have been generated in a reasonable scope, with two decision variables, including the time for loading and unloading container task with boxes as well as the empty driving time from completing a task to performing the next task, and then the representative data are analyzed. The uncertainty factors, such as the traffic control and traffic jam, are taken into account. The results show that： The external uncertainties have limited impact on the minimum value of the last task end time, and they increase the working time to a certain extent but are not the decisive factors of increasing time. During the process of automated container terminal operation, a large quantity of AGV will not lead to higher operating efficiency. With the increase of the number of AGV, the impact of uncertainty factors on the minimum value of the last task end time will reduce, until there is almost no impact .Computational experiments have been conducted to verify the validity and practicality of the model.

Key words:automated container terminals; automated guided vehicle; linear program; dispatching and scheduling

中图分类号:U691.31; TP301.6

文献标识码:A

文章编号：1001-7445(2016)02-0589-09

doi:10.13624/j.cnki.issn.1001-7445.2016.0589

通讯作者：胡志华(1977—)，男，湖南长沙人，上海海事大学教授，博士后，博士;E-mail：zhhu@shmtu.edu.cn。

基金项目：国家自然科学基金青年项目(71101088)；国家自然科学基金面上项目(71471109)；上海市曙光计划项目(13SG48)；上海市教委科研创新项目(14YZ100);交通部应用基础研究项目(2015329810260)

收稿日期：2015-11-11；

修订日期：2016-01-07

引文格式：马越汇,胡志华.不确定环境下自动化集装箱码头AGV调度与配置问题[J].广西大学学报(自然科学版)，2016，41(2)：589-597.