基于分岔理论的孤立微网静态电压稳定性分析

李苏川，吕智林，谭　颖

(广西大学电气工程学院， 广西南宁530004)



基于分岔理论的孤立微网静态电压稳定性分析

李苏川，吕智林，谭颖

(广西大学电气工程学院， 广西南宁530004)

摘要：为了深入研究孤立微网的静态电压稳定性问题，将分岔理论应用于微网静态电压稳定性分析研究。以鞍结分岔点作为电压稳定临界点，采用连续潮流(CPF)算法对四节点小型孤立微网进行电压稳定性分析，追踪出该系统的PU曲线，并根据特征根来判断该曲线上是否存在鞍结分岔点。分别计算出含SVC和不含SVC系统的电压稳定极限，得出负荷节点处电压稳定裕度。由实验结果可以看出，随着负荷参数的不断增大，负荷所需功率和发电机的输出功率也会随之增大，当达到它的传输极限时就会产生鞍结分岔现象，从而导致系统电压出现跌落甚至崩溃的现象。结果表明，利用上述方法可以有效地计算出孤立微网的电压稳定极限，并且使用SVC控制器可以提高系统电压稳定性。

关键词：电压稳定；孤立微网；连续潮流；鞍结分岔；SVC

0引言

微电网在提高用户供电可靠性、电力利用率和电能质量等方面具有重要作用。随着我国经济的飞速发展以及对电力需求的日益增加，微电网越来越受到人们的重视，微电网方面的研究逐渐成为电力系统分析当中的一大热点，特别是独立微网的电压稳定性研究[1-2]更是当前所面临的一大挑战。针对这一发展趋势，借鉴以往电压崩溃事故的经验和教训，结合电压稳定的安全指标对电压崩溃的发生机理和分析方法进行深入研究，从而提出改善系统电压稳定和预防系统电压崩溃的措施。

从数学角度来说，小型孤立微网和大电网都是一个大规模的非线性动态系统，其电压稳定性态的改变实质上就是该系统从一种稳定运行的形态走向不稳定即分岔的过程。目前国内外有许多学者利用分岔理论来研究大型电力系统的电压稳定性，并已经取得了很大进展。文献[3-5]从传统的潮流计算的角度研究了含风电场的静态电压稳定性，其主要分析方法是基于风电场静态分析的最大功率法[6]，但是常规的潮流雅可比矩阵在静态电压稳定临界点难以收敛，会造成最大功率的追踪出现误差。随着柔性交流输电系统(FACTS)技术的不断完善，目前常用的FACTS的装置大致分为两种，即静止无功补偿器(SVC)和STATCOM，这两种装置对系统的电压稳定性都有一定的效果。文献[7]利用分岔理论研究含SVC装置对电压稳定的影响。但前人大多是从大电网的背景出发来研究电网的电压稳定性，主要考虑分布式发电系统并网后对大电网的电压影响情况[8-9]。实践表明，分岔理论是对非线性系统进行结构稳定性分析的有力工具，但目前尚少有涉及小型孤立微网的研究。

本文针对小型孤立微网，从静态电压分析的角度去研究孤立微网可能存在的静态分岔点，建立微网系统的潮流数学模型，利用连续潮流法[10-13]消除系统潮流雅可比矩阵在临界点附近的奇异性，从而找到系统的近似临界点，同时完整地描绘出系统的PU曲线，找出导致系统电压崩溃的分岔点，并给出该系统电压稳定的裕度。分别对含SVC和不含SVC系统进行了仿真分析，成功搜索出该系统中导致电压崩溃的静态分岔点，通过对比验证了SVC能提高系统的电压稳定性。

1静态分岔研究的理论基础

电力系统静态稳定性的数学模型一般可用下述代数方程组表示，即：

f(x,λ)=0，f:Rm+p→Rm，

(1)

又可表示为:

f=[f1,f2]T，

(2)

式中，f1表示有功潮流方程；f2表示无功潮流方程；x为系统静态状态变量，包括节点电压幅值以及相角；λ为反映系统负荷水平的标量，即控制参数。

所有满足式(1)的点(x,λ)称为系统的平衡点，系统的平衡解流形可表示为：

M={(x,λ)∈Rm+p/f(x,λ)=0}，

(3)

它的扩展向量场雅可比矩阵为：

Df(x,λ)=[Dxf|Dλf]，

(4)

式中，Df是f在点(x,λ)处的导算子。

当系统的控制参数连续变化，直至λ=λ0时，根据分岔理论的基本知识，可将平衡解流形M上的静态分岔点分为以下几种类型[14]：

①双曲平衡点：当导算子Dxf(x0,λ0)无实部为零的特征值时，其中对应的点(x0,λ0)就称为平衡解流形M上的双曲平衡点。

②鞍结分岔点：当导算子的秩rank[Dxf(x0,λ0)]=m-1且保证rank[Dxf(x0,λ0)|Dλf(x0,λ0)]=m，而且相对应的参数δ有x(δ0)=x0，λ(δ0)=λ0，且满足：d2λ(δ0)/dδ2≠0，那么我们把能同时满足上述条件的所有的点(x0,λ0)称为平衡解流形M上的鞍结分岔点。

③普通静分岔点：当rank[Dxf(x0,λ0)|Dλf(x0,λ0)]=m-1，且在点(x0,λ0)处有不同斜率的解分支相交，则称点(x0,λ0)为平衡解流形M上的普通静分岔点。

根据分岔理论，鞍结静分岔点实质上是从稳定走向失稳的临界点。对于微网而言，当系统的控制参数逐渐变化达到某一极限值λ=λmax时发生鞍结分岔，此时系统会失稳，会出现电压跌落的情况。因此，对于小型微网，找到这一临界点，确定出分岔点的位置和类型，找到系统的稳定裕度，避免出现电压失稳是很有意义的。

2连续潮流算法(CPF)

连续潮流法又称为延拓潮流法，也称曲线跟踪法，是研究电力系统电压稳定性非常实用的工具。该算法是从系统的初始稳定点出发，随着负荷参数的逐渐增加，依次计算出系统的潮流解，直至计算出稳定临界点的一种方法。PU和QU曲线常被用来分析电力系统的电压稳定性和电压崩溃，这些曲线实际上反映了电力系统随负荷和发电机功率变化的稳态行为。根据式(1)所对应的电力系统静态稳定性的数学模型，用常规潮流程序可计算出基本潮流解(x(0),λ(0))，我们的目的是要得到在参数λ变化范围内潮流的解路径(x(i),λ(i))。一般来说，潮流方程的个数为n=2n1+n2，其中，n1、n2分别代表系统中的PQ和PU母线个数。

图1　典型电力系统鼻型曲线Fig.1　Typical power system nose type curve

随着负荷的不断增长，电力系统越来越接近稳定运行边界。图1为典型电力系统的鼻型曲线。随着参数λ的缓慢变化，在系统运行的状态到达“鼻尖”即A点之前，系统表达式在f(x,λ)=0时,它所对应的雅可比矩阵都具有负实部的特征值；在到达A点时，系统所对应的雅可比矩阵有且只有1个零特征值，也就是我们常说的奇异点。显而易见，A点将系统的PU曲线分成上下两个分支，分别对应于系统的电压稳定与不稳定，在鞍结分岔点处，稳定平衡点的曲线分支与不稳定平衡点的曲线分支相交，随着系统参数不断增大，平衡点将消失。通常情况下，当系统的运行状态达到“鼻尖”时，系统的潮流解方程将变为病态方程，用常规的牛顿法潮流方程去求解时方程将难以收敛, 而CPF采用延拓法来跟踪负荷和发电机功率变化情况下电力系统的稳态行为，它通过求解增广潮流方程得到穿越雅可比矩阵奇异点的解曲线，因此不会碰到病态矩阵造成的数值求解困难。

2.1系统的连续潮流模型

当系统的负荷水平和发电机输出功率确定时，在极坐标下系统的常规潮流基本方程可写为：

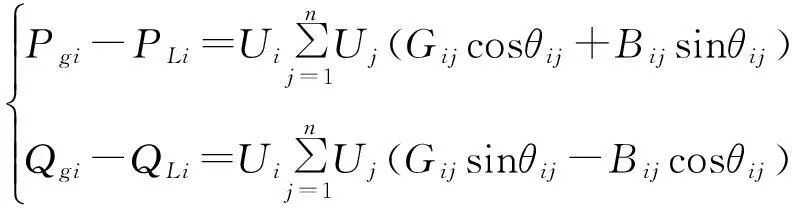
(5)

式中，Pgi为发电机节点处有功功率，Qgi为对应的无功功率；PLi为负荷节点处的有功功率，QLi为对应的无功功率；U，θ分别为节点电压幅值和相角。n代表节点总数，i,j表示节点号，Gij代表i,j节点间的电导，Bij代表i,j节点间的电纳。

连续潮流法的基本方程为：

f(x,λ)=F(x)+λb=0，

(6)

式中，x为系统静态状态变量(即节点电压幅值或相角)；F(x)对应常规潮流方程；b为表示系统节点发电机、负荷功率变化方式(方向和大小)的向量；λ为反映系统负荷功率变化量的标量参数。

含有负荷变化为参数的连续潮流方程为：

(7)

式中，kpg，kpl，kql分别表示发电机有功功率变化的方向向量和负荷有功以及无功变化的方向向量。

2.2连续潮流计算步骤

如果采用向量和矩阵形式[17]来表示系统的潮流方程，有：

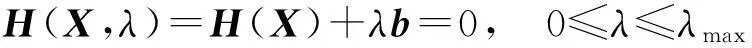
(8)

式中，X为状态变量，表示系统节点的电压或相角。

连续潮流计算步骤[15]：

①预估步。引入参数后的潮流方程状态变量为(X,λ)T。首先采用切线预估的方法来预估状态变量的下一步解，对式(8)进行全微分，在初始点X0展开，得到：

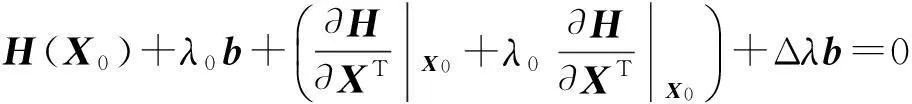
(9)

由于引入了参数λ使得系统的潮流方程增加了1个状态变量，此时要增加一维关于λ的规范化方程，那么系统的潮流雅可比矩阵也相应地增加了1行1列，则系统扩展后的潮流方程可写为：

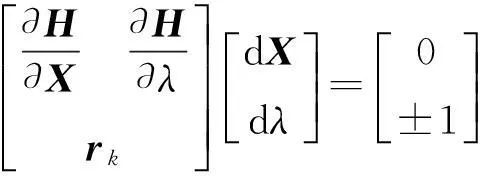
(10)

由式(10)可以得到方程组的切向量，步长因子设为μ，则方程的下一步预测解为：

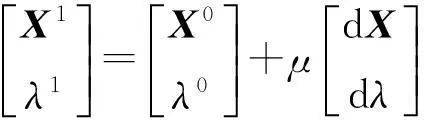
(11)

②校正步。在校正步中，将预估值代入扩展后的潮流方程(10)作为迭代求解。由于系统增加了1个独立变量λ，使得待求量个数要比方程个数多1个，这时要指定1组状态变量(X,λ)T，将它的第r个分量Uk的值作为预估值，得到新的扩展潮流方程为：

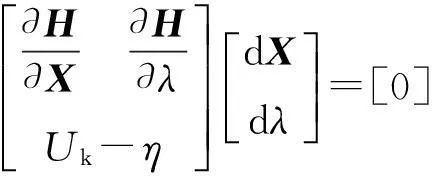
(12)

3小型孤立微网系统描述

搭建了1个小型微网模型，如图2所示。其简化模型由1个平衡节点(节点1)，4阶同步发电机节点(节点2)，1个蓄电池电源节点(节点4)以及1个负载节点(节点3，接SVC控制器)组成。系统基准功率SB=50 kVA。其中，U1，U2，U3，U4为各个节点的电压幅值；系统频率f=60 Hz；节点之间导纳分别为Y21、Y23、Y34和Y14。

图2　含SVC孤立微网系统模型

3.1主要节点的数学模型

①PV节点

PV节点有固定的电压值，所连母线注入的有功也有固定值，即：

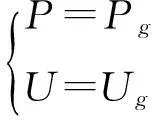
(13)

在分布式平衡节点的母线模型中，有功平衡方程为：

P=(1+γkG)Pg，

(14)

式中，kG是分布式平衡节点的可变参数，γ是损耗系数，潮流分析中要用到无功功率的限值，若达到无功极限值，则PV节点转化为PQ节点，有：

(15)

当算完潮流分布后，PQ母线要再次转化为PV母线。

②同步电机模型

该同步电机采用的是四阶模型，其数学表达式为：

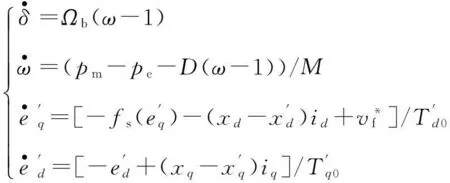
(16)

③负荷模型

负荷选用的是恒功率负荷，其数学模型为：

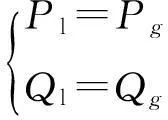
(17)

其所连母线注入的有功及无功为恒定值。

图3　SVC控制结构图Fig.3　Control chart of SVC

④SVC模型

静止无功补偿器(SVC)可以根据系统的需要向系统输送无功功率，或者从系统吸收无功功率，以便使系统达到无功功率平衡的目的，从而维持系统的电压稳定。其控制方式采用传统的PID控制方式，控制框图如图3所示。其简化的数学模型为：

(18)

此时，SVC向所连节点注入的无功功率为：

Q=bSVCU2，

(19)

式中，Uref为SVC模型的参考电压；Tr，Kr为SVC传递函数的时间常数和放大倍数；bSVC为SVC输出的等值电纳；U为补偿点采集到的电压。

4仿真分析

4.1不含SVC的系统

在利用连续潮流算法进行仿真时一般不考虑发电机的动态特性，本研究中，把发电机节点和蓄电池节点处理成PV节点，实验仿真参数如表1所示[Prat，Urat分别表示额定有功功率(MVA)和额定电压幅值(kV)，其余量的单位均为标幺值pu]。其中，节点间的导纳分别为Y21=0.05+0.19j，Y23=0.12+0.21j，Y14=0.1+0.16j，Y34=0.08+0.24j，用连续潮流算法对该系统的连续潮流模型进行仿真。图4给出了负荷节点处所需有功功率和无功功率随参数变化情况。可见，随着参数λ的增加，负荷需求也会增加，说明参数λ也直接反应了负荷需求的变化情况。

表2给出了参数λ迭代收敛过程。当参数λ从0逐步增大到1.608时，系统所对应的雅可比矩阵有1个零特征值，或者说奇异。图5给出了系统在“鼻尖”点特征值的分布情况。其中，Real表示特征根的实部，Imag表示虚部。可见，存在1个零特征根，由鞍结分岔定义可知系统此刻不稳定，发生了鞍结分岔，在计算出分岔点后λ开始减小直至0。

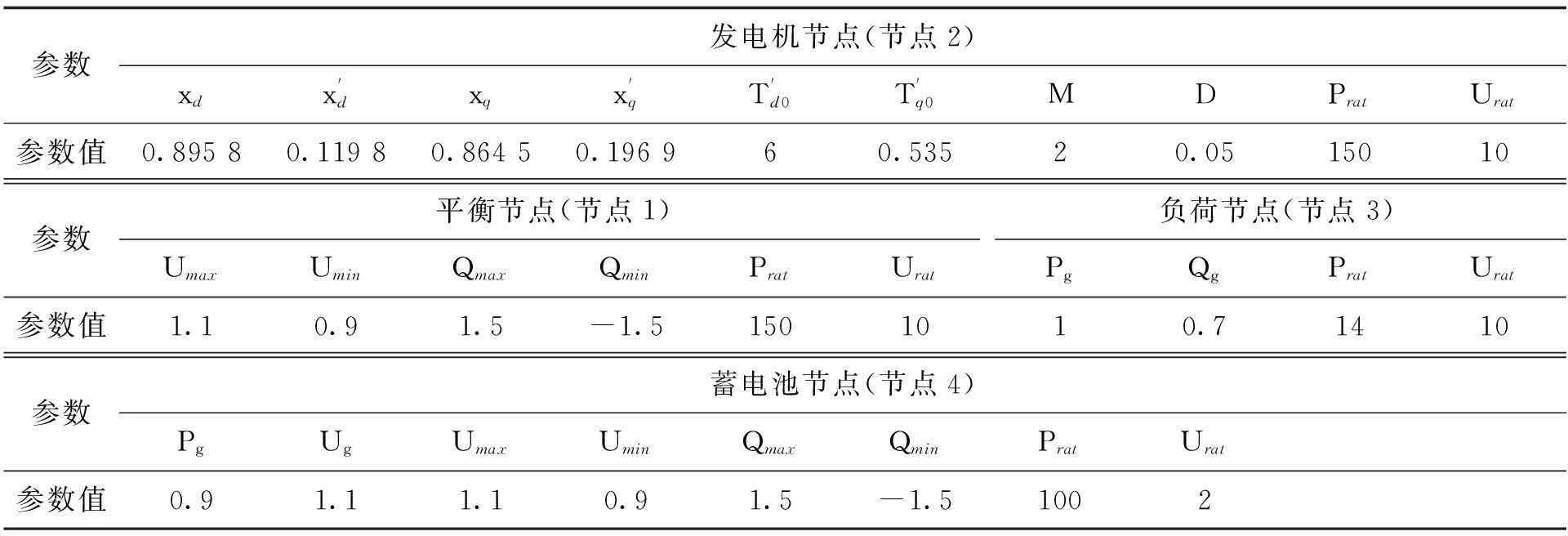
表1　不含SVC的系统参数取值

表2　参数λ迭代过程

图4负荷功率随参数λ的变化曲线

Fig.4Load power curve with parameters

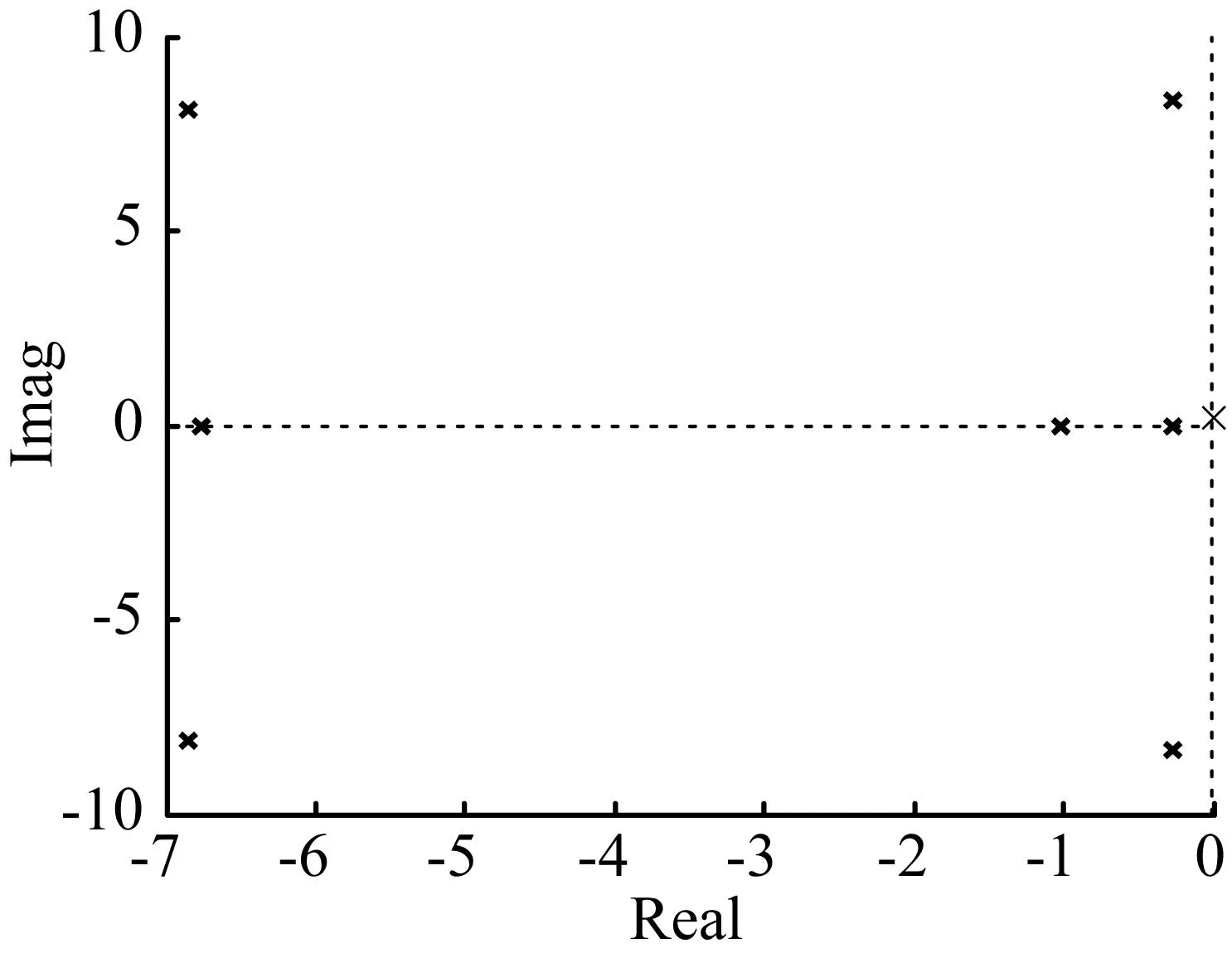
图5“鼻尖”处特征根的分布情况

Fig.5The characteristic root of “the tips”

图6给出了负荷节点处和发电机节点处的电压和相角随参数变化的情况。可以看到，电压和相角都在λmax=1.608处到达了曲线的“鼻尖”处，发生了鞍结分岔，此时系统是一个不稳定运行的状态，随着负荷的继续增大，该系统潮流方程发生鞍结点分岔将引起系统负荷节点处的电压崩溃。图7给出了在λmax=1.608(鞍结分岔点处)时，系统受扰后的仿真结果。可以看出，大约经过0.1 s后负荷节点处电压迅速下降，系统发生崩溃现象。这是由于系统平衡点数目发生变化引起的。

在物理意义上，随着参数的负荷需求的增加，发电机无功传输也会随之增大，当达到它的最大传输极限时就会发生鞍结分岔现象，这是由于电力网络达到最大传输能力所引起的，此时系统的连续潮流方程也会发生改变，发电机节点从PV节点改变为PQ节点。图8给出了发电机节点处的PU曲线，可见在发电机有功P=0.78时会产生分岔现象，此时节点电压会失稳。随着负荷需求的增大，发电机无功出力也会增大，当达到它的极限值时系统的输电能力也会下降，因为系统要传输更大的有功必须有一定的无功作为支撑。

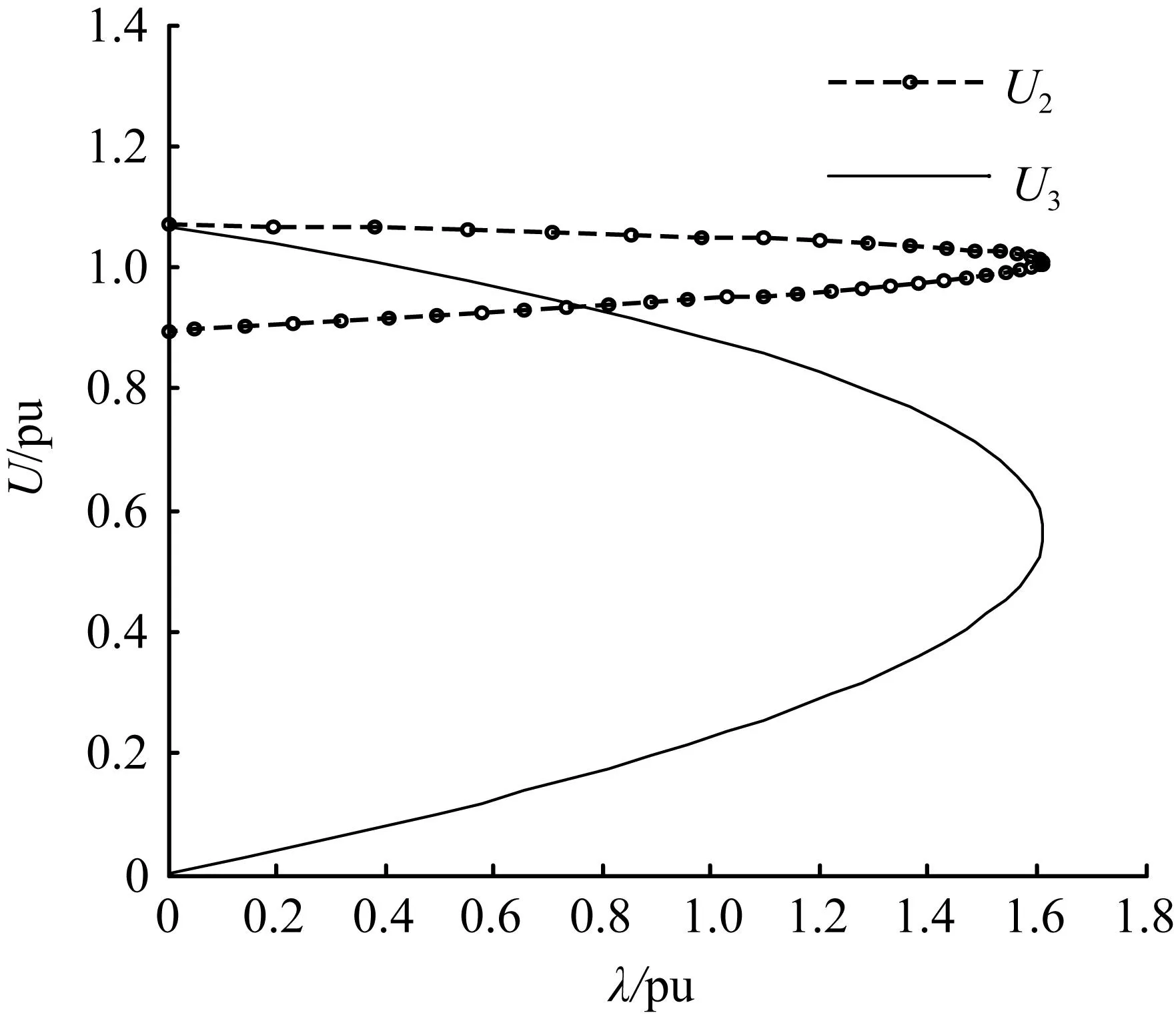
(a) 负荷和发电机节点处电压随参数λ的变化曲线

(b) 负荷和发电机节点处相角随参数λ的变化曲线

图6负荷和发电机节点处电压、相角随参数λ的变化曲线

Fig.6Curve of load and generator node voltage and phase angle with the change of parameterλ

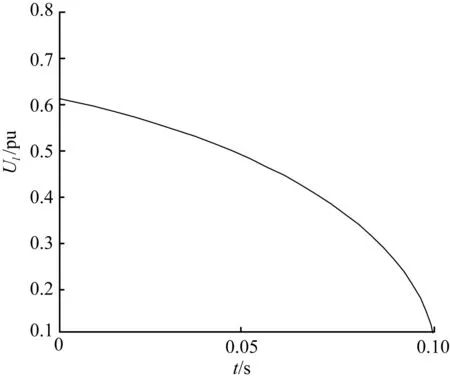
图7λmax=1.608时的时域仿真结果

Fig.7Time domain simulation results ofλmax=1.608

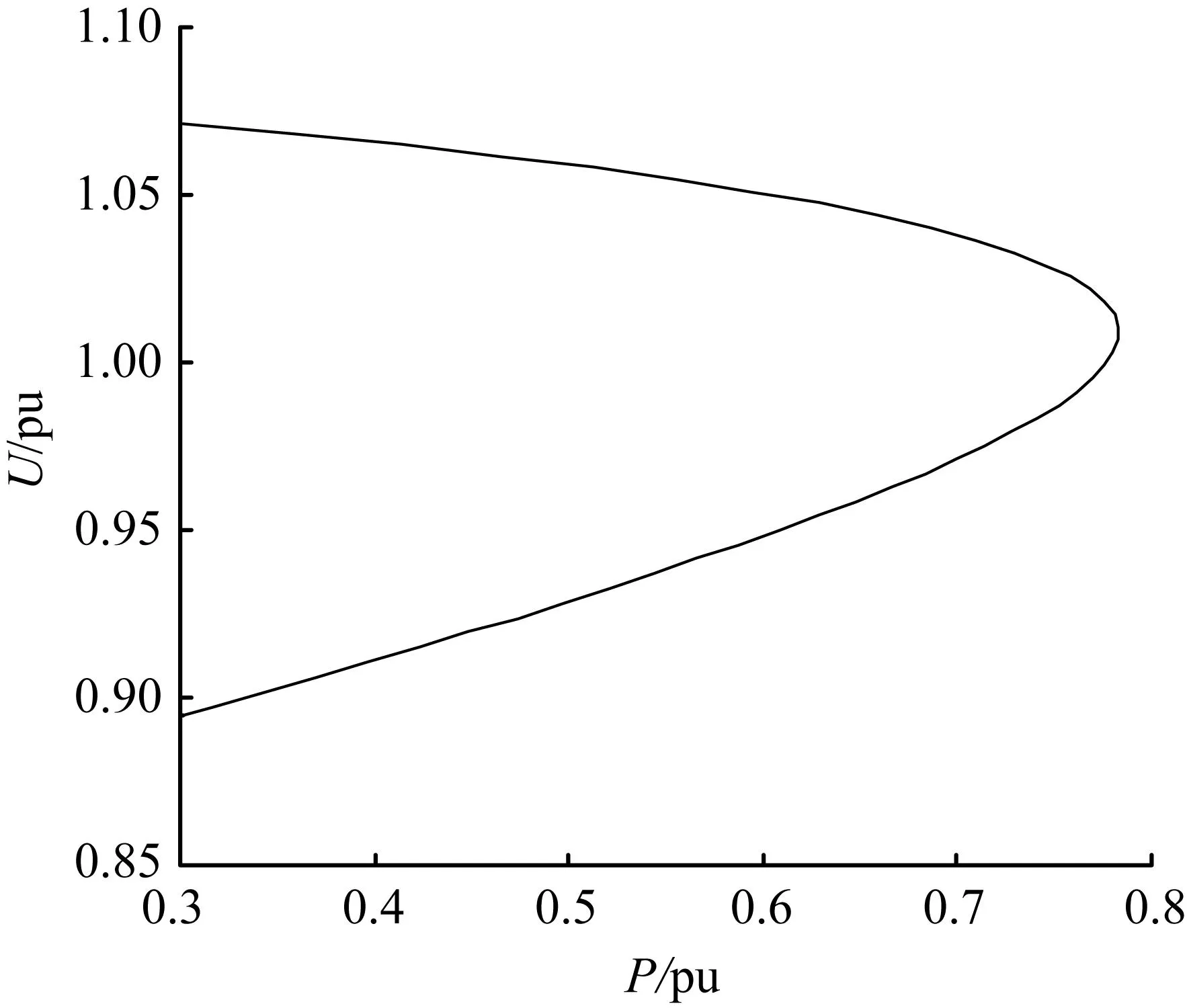
图8发电机节点处的PV曲线

Fig.8PV curve of generator node

4.2含SVC的系统

上述不含SVC的系统的仿真结果表明，随着负荷参数的增大，发电机无功出力也会增大，当达到它的输出极限时系统的输电能力也会下降，这是因为系统要传输更大的有功必须有一定的无功作为支撑，为此增加1个无功补偿装置(SVC)。在加装了SVC后，系统负荷节点、发电机节点处电压随参数λ的变化曲线以及发电机节点处的PU曲线如图9所示，其中SVC参数设置为：bmax=1，bmax=-1，Tr=1，Kr=10，Uref=1，其余参数和表1一致。

对比图6可以看出，加装SVC的系统在λmax=1.793 3 时系统达到了鼻尖点处，即发生鞍结分岔，而没有加装SVC的系统则在λmax=1.608时发生了鞍结分岔。可见SVC对延迟系统电压失稳有一定的效果，可以提高系统的稳定性。对比图8可以看出，SVC对提高发电机的输出功率也有很明显的效果。

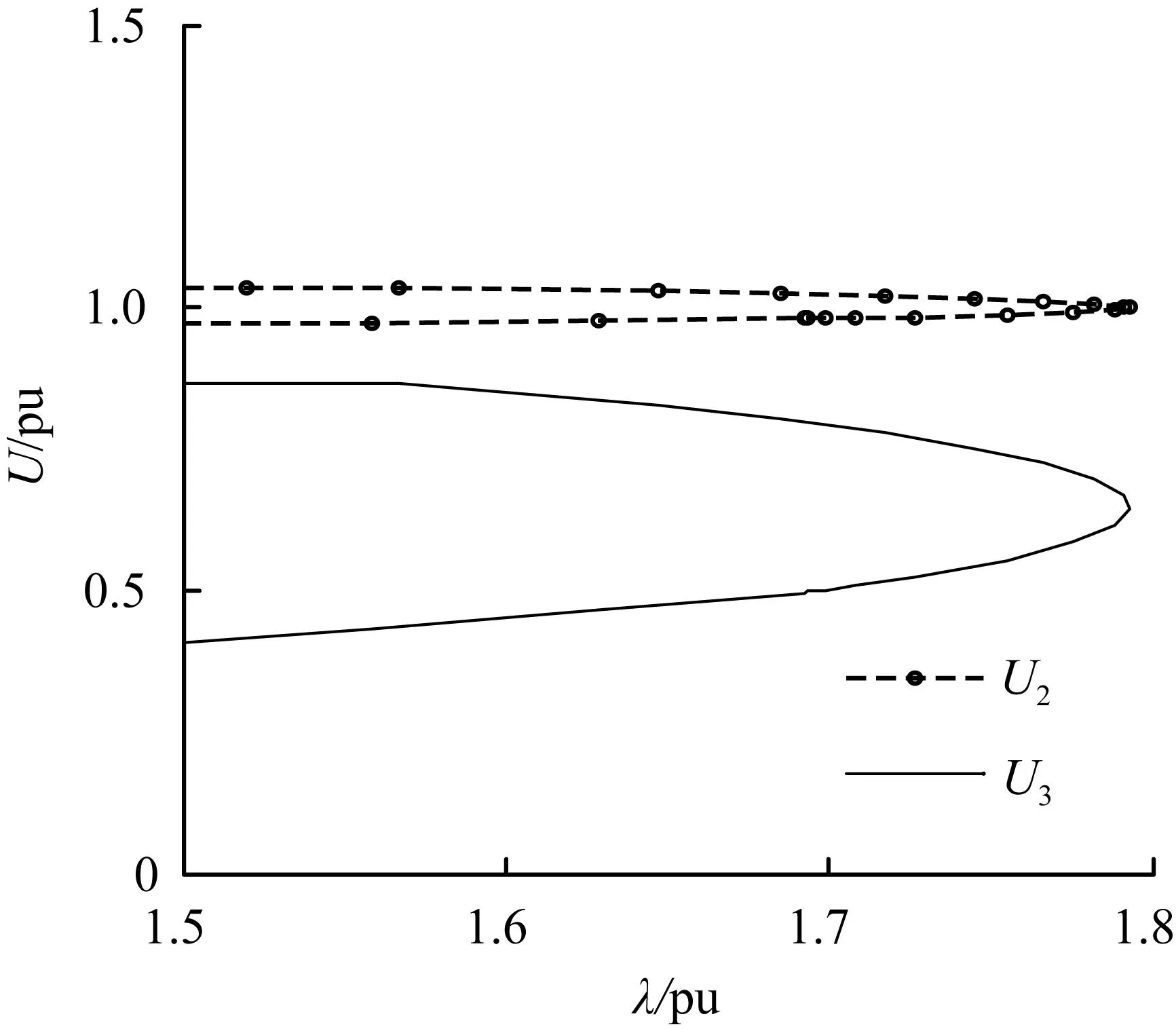
(a) 含SVC的节点电压随参数λ的变化曲线

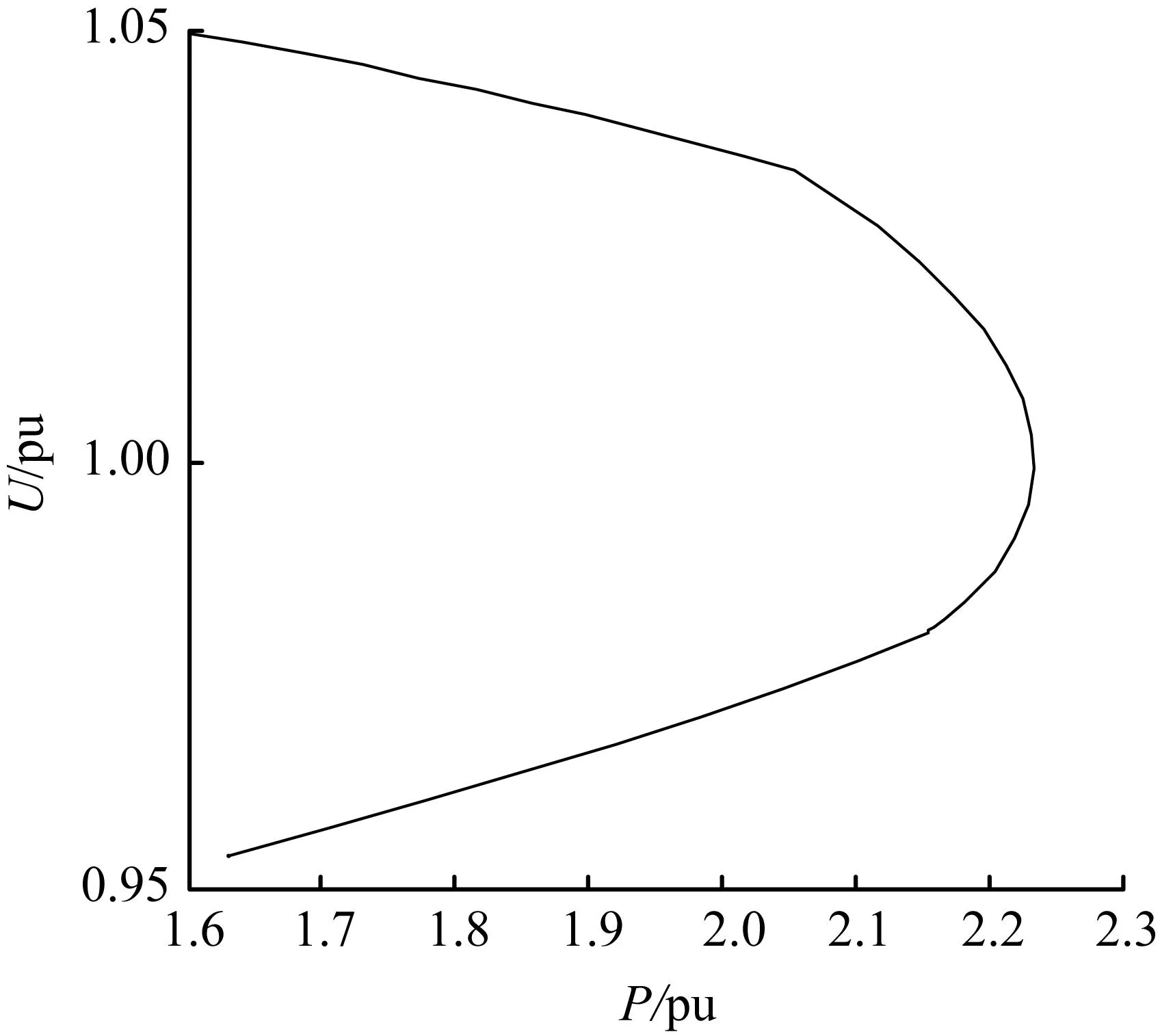
(b) 含SVC的发电机节点PU曲线

图9含SVC系统仿真图

Fig.9System simulation figure with SVC

5结语

本文采用分岔理论作为孤立微网电压稳定性分析研究的方法，利用连续潮流算法追踪出四节点孤立微网系统的PU曲线，并算出该曲线上的静态电压稳定临界点(鞍结分岔点)，给出该系统负荷节点处的电压稳定裕度。实验结果表明，随着负荷参数λ的不断增加，负荷所需功率也不断增加，此时发电机的功率传输也不断增加，当达到它的传输极限时就会产生鞍结分岔点，且该分岔点会导致负荷节点处的电压产生失稳。为了提高系统的稳定性，系统想要传输更大的有功必须要有一定的无功作为支撑，因此，对该系统增加了无功补偿装置(SVC)。对比分析的结果表明，通过增加SVC可以延迟系统鞍结分岔点的发生，增加负荷极限和发电机的输出功率，进而提高了系统电压稳定性。通过实验可以看出，利用这一方法同样可以很好地研究微网静态电压稳定性问题。

参考文献：

[1]张建华.微电网运行控制与保护技术[M]. 北京：中国电力出版社, 2010.

[2]杨维满, 王兴贵.光伏微源特性对串联型微网电压稳定性的影响[J]. 电网技术, 2013,9(9):2446-2451.

[3]薛振宇, 房大中.基于双向迭代的交直流互联电力系统潮流计算[J]. 电力系统自动化, 2013, 37(5):61-67.

[4]王海超, 周双喜, 鲁宗相,等.含风电场的电力系统潮流计算的联合迭代方法及应用[J]. 电网技术, 2005,29(18):59-62.

[5]吴义纯, 丁明, 张立军.含风电场的电力系统潮流计算[J]. 中国电机工程学报, 2005, 25(4): 36-39.

[6]张义斌, 王伟胜, 戴慧珠.基于P-V曲线的风电场接入系统稳态分析[J]. 电网技术, 2004, 28(23):61-65.

[7]杨秀, 金红核, 郭晨吉,等.应用分岔理论分析SVC对电力系统电压稳定性的影响[J]. 电力系统保护与控制, 2009, 37(7):7-11.

[8]KWATNY H G, PASRIJA A, BAHAR L.Static bifurcations in electric power networks: Loss of steady-state stability and voltage collapse[J]. IEEE Transactions on Circuits & Systems, 1986, 33(10):981-991.

[9]AIJARAPU V, CHRISTY C.The continuation power flow: a tool for steady state voltage stability analysis[J]. Power Systems, IEEE Transactions on, 1992, 7(1): 416-423.

[10]CAO G Y, HILL D J, HUI R.Continuation of local bifurcations for power systemdifferential-algebraic equation stability model[J]. IEEE Proceedings-Generation, Transmission and Distribution, 2005, 152(4): 575-580.

[11]马幼捷,张继东,周雪松,等.基于分岔理论的含风电场电力系统静态电压稳定问题研究[J]. 电网技术, 2008,32(9):74-79.

[12]阳育德,韦化.基于L_1范数和现代内点理论的电力系统潮流计算[J]. 广西大学学报(自然科学版), 2007,32(S1):22-26.

[13]彭志炜,胡国根,韩祯祥.基于分叉理论的电力系统电压稳定性分析[M]. 北京：中国电力出版社, 2005.

[14]杨超,沈聪,李睿.含分布式电源配电网前推回代潮流算法中处理PV节点新方法[J]. 电网技术, 2012, 36(9):238-243.

[15]周双喜,朱凌志,郭锡玖.电力系统电压稳定性及其控制[M]. 北京：中国电力出版社, 2004.

(责任编辑裴润梅)

Analysis on static voltage stability of isolated micro-grid based on bifurcation theory

LI Su-chuan， LYU Zhi-lin， TAN Ying

(College of Electric Engineering, Guangxi University, Nanning 530004, China)

Abstract:In order to study the problem of static voltage stability of isolated micro-grid, the bifurcation theory is applied. The saddle node bifurcation point is used as the voltage collapse critical point while using continuous power flow (CPF) algorithm to analyze the voltage stability of a small isolated micro-grid with four nodes. Then by tracing the PU curve of the system and according to the characteristics of the root the saddle node bifurcation point in the curve is determined. The stability limit of the SVC and non SVC system voltage are calculated respectively to obtain the voltage stability margin of load node. The experiments show that with the increase of the load parameters, the required power of the load and the output power of the generator will increase. Then the saddle node bifurcation will occur when the transmission limit which causes the system voltage to fall or collapse. The results of simulations show that the voltage stability limit of isolated micro grid can be calculated by using this method. And by using SVC controller the stability of system voltage can be improved.

Key words:voltage stability; isolated micro-grid; continuous power flow; saddle node bifurcation; SVC

中图分类号：TM61

文献标识码：A

文章编号：1001-7445(2016)02-0488-10

doi:10.13624/j.cnki.issn.1001-7445.2016.0488

通讯作者：吕智林(1971—)，女，广西南宁人，广西大学教授，博士；E-mail: luzhilin2001@163.com。

基金项目：国家自然科学基金资助项目(61364027)

收稿日期：2015-11-27；

修订日期：2016-01-18

引文格式：李苏川，吕智林，谭颖.基于分岔理论的含SVC小型孤立微网静态电压稳定性分析[J].广西大学学报(自然科学版)，2016，41(2)：488-497.