基于NARX神经网络的轨道垂向不平顺估计

王　贵，邢宗义，蒋　杰，黄　文

(1.南京理工大学自动化学院， 江苏南京210094；2.南京理工大学机械工程学院， 江苏南京210094)



基于NARX神经网络的轨道垂向不平顺估计

王贵1，邢宗义1，蒋杰2，黄文2

(1.南京理工大学自动化学院， 江苏南京210094；2.南京理工大学机械工程学院， 江苏南京210094)

摘要：轨道不平顺是影响车辆平稳性和安全性的关键因素，因此及时掌握轨道不平顺的状态对保障列车运营具有重要意义。针对单个惯性量较难达到对不同波段不平顺的检测，提出一种采用非线性自回归神经网络(Nonlinear Auto-Regressive with exogenous Input Neural Networks, NARX)的轨道不平顺估计方法。以实测高铁轨道不平顺数据作为输入，通过车辆—轨道垂向耦合动力学模型仿真得到多个惯性量数据，再将归一化的多个惯性量仿真数据作为神经网络的输入，轨道不平顺作为输出，并用均方根误差和相关系数进行网络性能评价。仿真结果表明，NARX神经网络模型估计结果的均方根误差为0.028 9，相关系数为0.939 5，优于反向传播(BP)神经网络模型的均方根误差0.086 8和相关系数0.641 8，NARX神经网络拟合效果更好，表明本文所提方法能精确有效地实现轨道垂向不平顺估计。

关键词：轨道不平顺；在线监测；NARX神经网络；估计

0引言

轨道不平顺主要由于轮轨反复作用及轨道枕木等恶化造成的，它是产生车辆随机振动、恶化轨道结构疲劳、降低车辆运行安全性的主要影响因素[1-2]。

目前国内外已见众多轨道不平顺在线监测的研究。Resendiz E等[3]在运营车辆上加装机器视觉仪器，构成轨道不平顺在线监测系统，然而机器视觉所用仪器成本高，且对环境状况较为敏感，难以满足在线实时监测的要求。Montalban Domingo M L等[4]通过安装轴箱振动传感器来检测轨道垂向不平顺，并对轴箱振动加速度信号进行二次积分、高通滤波和相位补偿、振动模型逆输入的处理，实现轨道不平顺的检测。朱文发等[5]提出基于捷联惯性系统实现轨道长波不平顺的检测方法。但是仅以单个惯性量较难实现对不同波段不平顺的检测，因此须选取多个惯性量以监测轨道不平顺。

在惯性监测轨道不平顺中，Lee J S[6]等提出一种通过测量包括车体、转向架和轴箱在内的车辆振动响应进行轨道长波不平顺识别。Li M X D[7]等提出了一种由轨道、车辆以及轮轨耦合的更接近实际的轮轨力学模型，通过快速傅里叶变换到频域求解动力学模型，然后利用输入输出数据建立线性系统逆模型，实现垂向轨道几何状态评估。而这些方法都需要建立复杂的力学模型，而本文采用智能优化算法非线性自回归神经网络(NARX神经网络)实现对轨道不平顺的估计，不需要考虑车辆轨道之间复杂的数学模型。

综合考虑轴箱垂向振动、构架垂向振动和构架点头角速度三个惯性量，采用NARX神经网络构建多输入，轨道垂向不平顺输出的数学模型，以达到精确的轨道不平顺估计。

1惯性监测基本原理

车辆的转向架由车轮、轴箱、一系簧、构架和二系簧等组成。在运营车辆上安装轴箱垂向振动加速度计、构架垂向振动加速度计和构架点头陀螺仪(如图1，其中陀螺仪位于轴箱的正上方)，在转向架另一侧相同的位置安装传感器，即可构成对左右轨道垂向不平顺的在线监测。

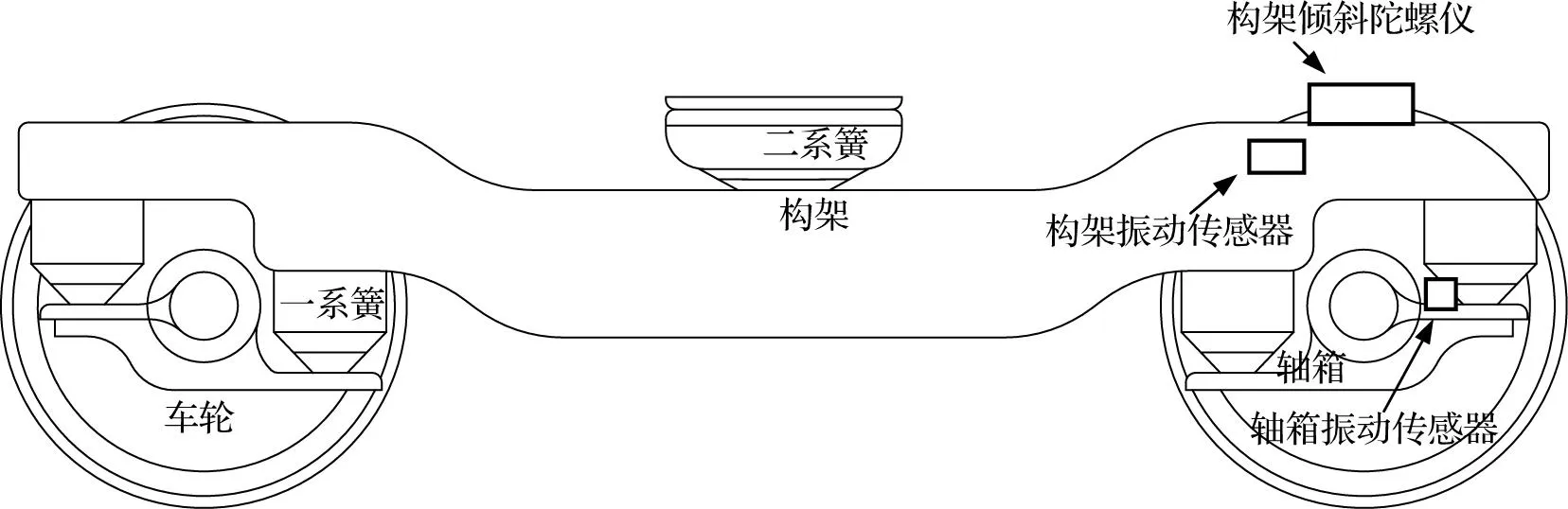
图1　传感器安装图

①轴箱振动加速度

将轴箱垂向加速度等效为车轮垂向加速度，轴箱垂向加速度信号对时间两次积分就转换成轨道垂向位移估计；轴箱垂向加速度除以车速的平方，而后相对空间步长两次积分即得到垂向位移估计如下式：

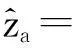
(1)

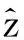
轴箱加速度与轨道位移之间的关系，会受到轴箱与车轮之间的滚动轴承、车轮不圆度、车轮踏面与轨道之间的非刚性接触关系以及环境噪声等[8]的影响，造成估计偏差。轴箱加速度的一个较大缺点是当车辆经过轨道局部故障时，轴箱加速度的值高达100 g，而在轨道长波不平顺时加速度往往小于1 g，因此仅适合于检测短波和局部不平顺。

②构架振动加速度

构架垂向振动同样通过两次积分即得到垂向位移估计。忽略一系簧，构架垂向运动依据前后车轮垂向运动的均值来确定。在轨道不平顺波长远高于构架轴距情况下，构架的垂向振动波长接近轨道垂向几何波长。在波长低于2倍轴距时，构架的垂向振动检测轨道垂向几何状态存在不确定的滤波特性。构架上的加速度和轴箱上的强振动输出是隔离的，所以它测量范围要求较小，可以在传感器线性度和信噪比低的情况下提供长波的信息。

③构架角速度检测长波不平顺

列车前进时构架点头陀螺仪输出的角度φ等于轨道的俯仰角，则相应的轨道垂向位移估计如下式：

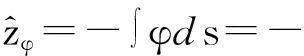
(2)

由式(2)可知，时域采样的角速度信号，可通过两次积分并乘以速度后得到垂向位移估计；空间域采样的角速度信号，可直接对空间步长两次积分得到垂向位移估计。

构架倾角等于前后轮的垂向位置差除以构架轴距。轴距大小决定了构架倾角和轨道垂向不平顺之间的几何滤波特性。对于轴距为2.5 m的车辆，当轨道不平顺波长大于2倍的轴距时，构架倾角能准确反应轨道平顺状态(0 dB)；当波长为2.5 m即等于轴距的情况时几何滤波增益迅速下降到零；当波长小于2.5 m时，通常为轨道局部故障，构架倾角会有额外的微小输出。

轨道不平顺包含1～300 m波长的不平顺以及小于1 m的轨道局部故障，仅以轴箱垂向振动、构架垂向振动或构架点头角速度中单一惯性量不能精确估计各个波长的轨道不平顺，故将该三个惯性量同时作为估计轨道不平顺的NARX神经网络的输入，从而避免了单惯性量估计不全面的缺陷。

2NARX神经网络

NARX神经网络是一个有着外部输入的非线性自回归网络，它有一个多步时延的动态特性，并通过反馈连接封闭网络的若干层[9]。

2.1网络结构

NARX神经网络结构包括输入层、输出层、隐层和承接层[10]，如图2所示。其中输入信号通过承接层传递给隐层，隐层对输入的信号进行处理后传递到输出层，输出层将隐层输出信号做线性加权获得最终的神经网络输出信号，承接层将网络反馈的信号和输入层输出的信号进行延时，然后输送到隐层。

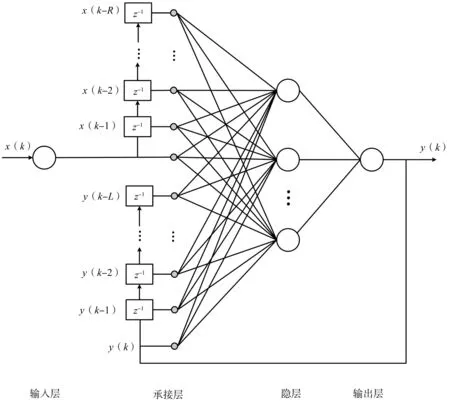
图2　NARX神经网络结构示意图

设NARX神经网络有M个输入层，在承接层中输入时间延迟阶数和输出时间延时阶数分别为R和L，并且网络单输出，则隐层节点j的输出Oj如下式：

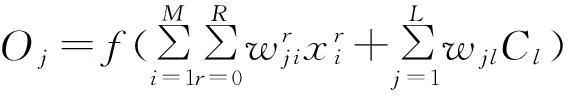
(3)

输出层第k个神经元的输出为：

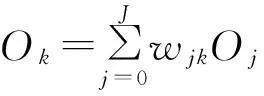
(4)

其中，wjk为隐层第j个输出与输出层第k个神经元之间的连接权值。

2.2贝叶斯正则化算法

神经网络常用的训练算法主要有动态反向传播(BP)算法和贝叶斯算法等[11]。而动态BP算法因为计算复杂度高从而学习效率较低。贝叶斯正则化算法[12]通过优化神经网络性能评价函数来提高其泛化能力从而达到降低网络的复杂度的目的，在神经网络训练过程中通过自动调整网络性能评价函数系数α与β使网络性能达到最优，网络性能评价函数为：

F(ω)=α·Ew+β·ED，

(5)

2.3输出评价

神经网络模型性能通过均方根误差(Root Mean Squared Error,RMSE)来衡量：

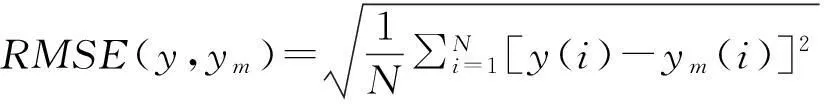
(6)

式中，N为测试样本个数，y为测试样本的真实值，ym为模型的输出值。当RMSE值越小时，表示模型精度越高，越接近实际系统。

为了对轨道不平顺估计输出和实际输出关系进一步描述，通过相关系数R来衡量两者的相关程度：

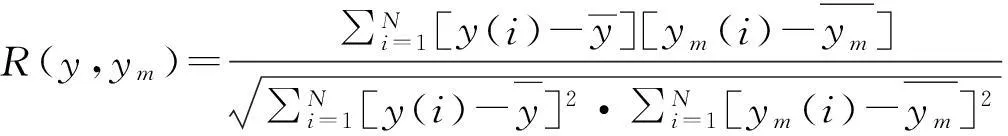
(7)

3实例分析

3.1数据准备及区分

以实测轨道不平顺数据作为输入，并建立车辆—轨道垂向耦合动力学仿真模型，得到轴箱加速度、构架点头角速度、构架加速度等仿真信号。

车辆—轨道垂向耦合系统模型是研究车辆—轨道在垂直方向离散点动态相互作用的理论工具，包括车辆子模型、轨道子模型和轮轨接触模型。车辆子模型包括车体、前后构架的沉浮、俯仰运动，四个轮对的沉浮运动；轨道子模型采用连续支撑的欧拉梁力学模型；轮轨接触模型应用Hertz非线性接触理论。模型采用Zhai W等[13]提出方法求取模型的动力学响应。

考虑到输入和输出数据数量级存在不同，有时数量级会有较大的差别。而在神经网络建模中，输入和输出数据数量级差别很大将影响网络的收敛[14]，因此，将输入和输出数据归一化至[0，1]范围内：

(8)

其中，xi为未经归一化处理的原始数据，xmax为变量x的最大值，xmin为变量x的最小值。

以某段高铁线路综合检测车实测的垂向轨道长波不平顺数据作为动力学模型输入。该段实测垂向轨道长波不平顺数据来自中国铁道科学研究院，是以0.5 m为间隔的离散采样序列，长度2 km。为模拟列车运行摩擦阻力和传感器观测噪声等其他因素对轨道不平顺谱的影响，本文在轨道不平顺谱上叠加5%的随机白噪声。共采集输入输出数据10 000对，其中前8 000对数据用于神经网络训练，后2 000对数据用于神经网络估计，输入输出数据归一化后如图3所示。

3.2结果分析

为了确定神经网络模型隐节点数目和时延阶数等参数，采用专家经验法和试凑法确定隐节点数目为20，时延阶数为45。

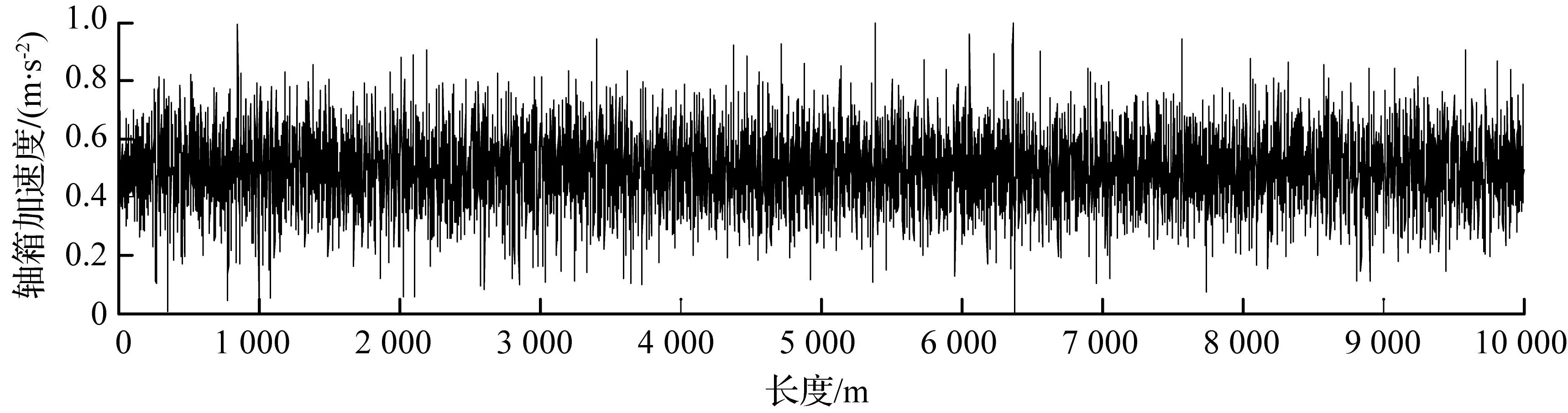
(a) 轴箱垂向振动

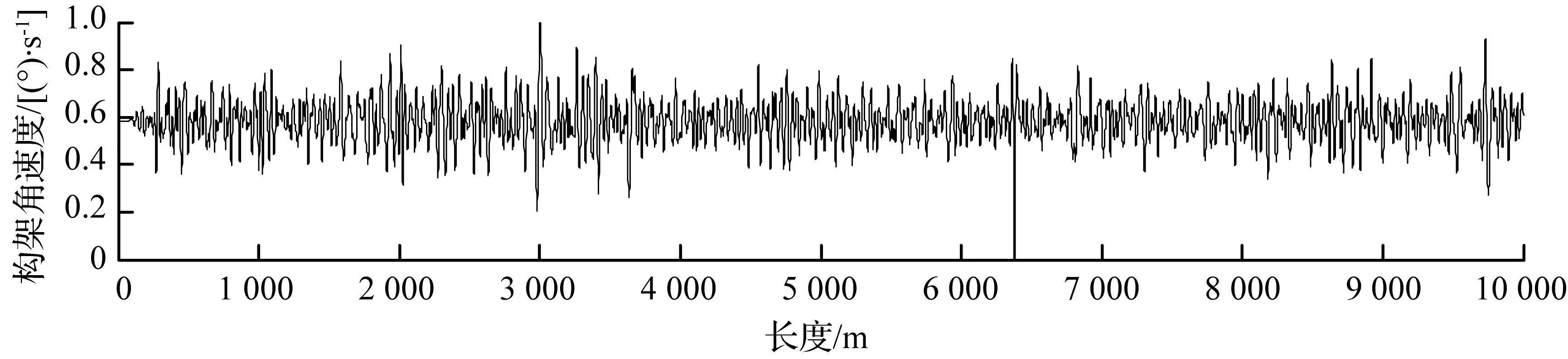
(b) 构架垂向振动

(c) 构架点头角速度

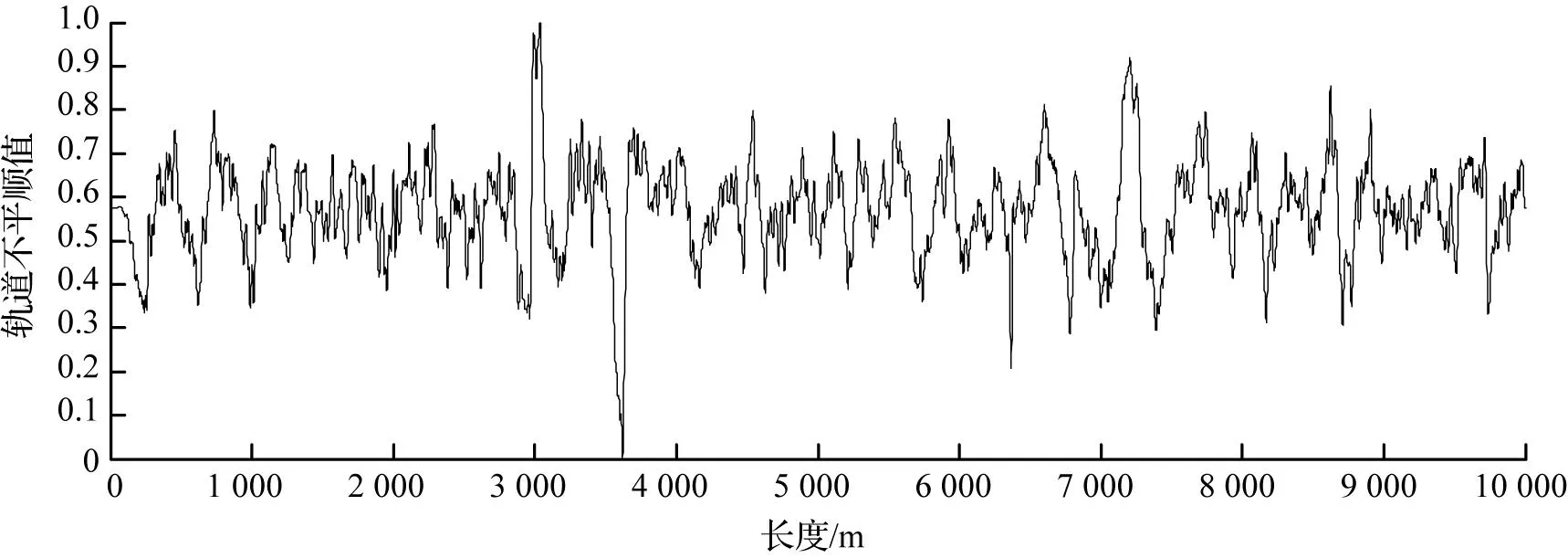
(d) 轨道不平顺

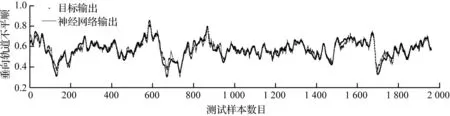
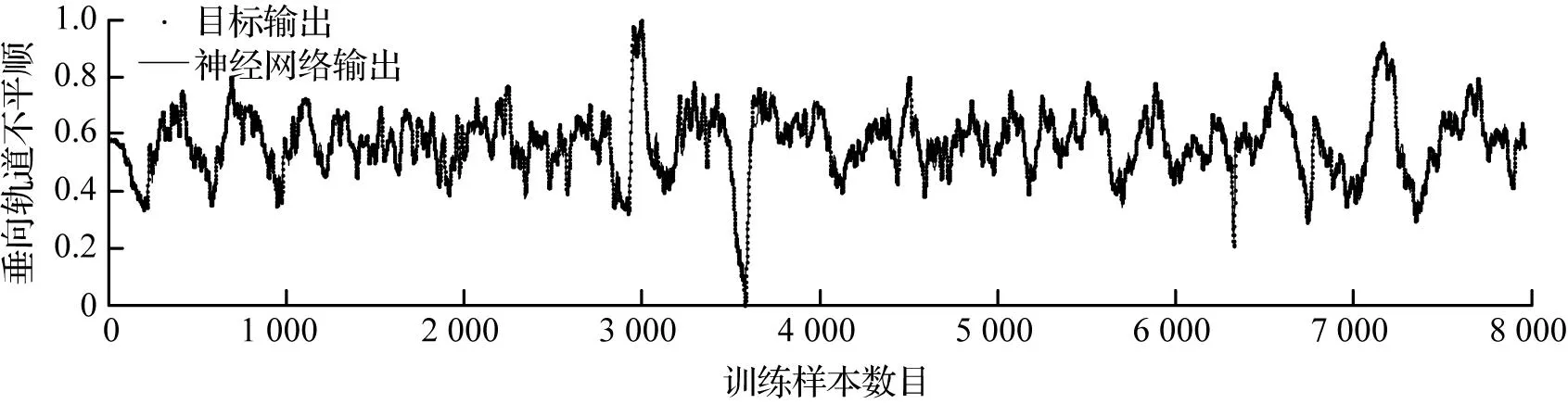
采用贝叶斯正则化算法训练NARX神经网络，模型输出与实际输出的误差图比较如图4所示， NARX神经网络输出与实际输出的相关性分析如图5所示。由图4和图5可见，NARX神经网络输出与目标输出趋势基本相同且相关性很高，从而能较好地实现轨道不平顺的估计。

(a) 训练数据与NARX神经网络输出比较

(b) 测试数据与NARX神经网络输出比较

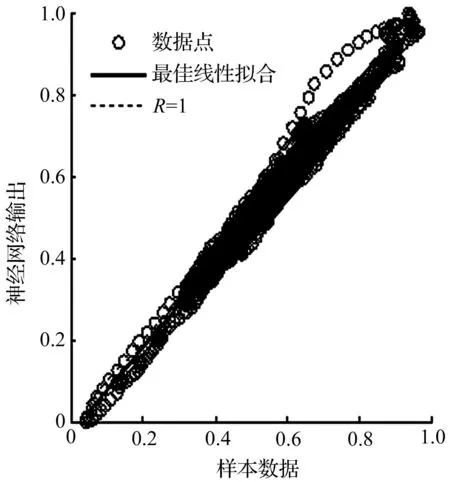
(a) 训练数据相关性

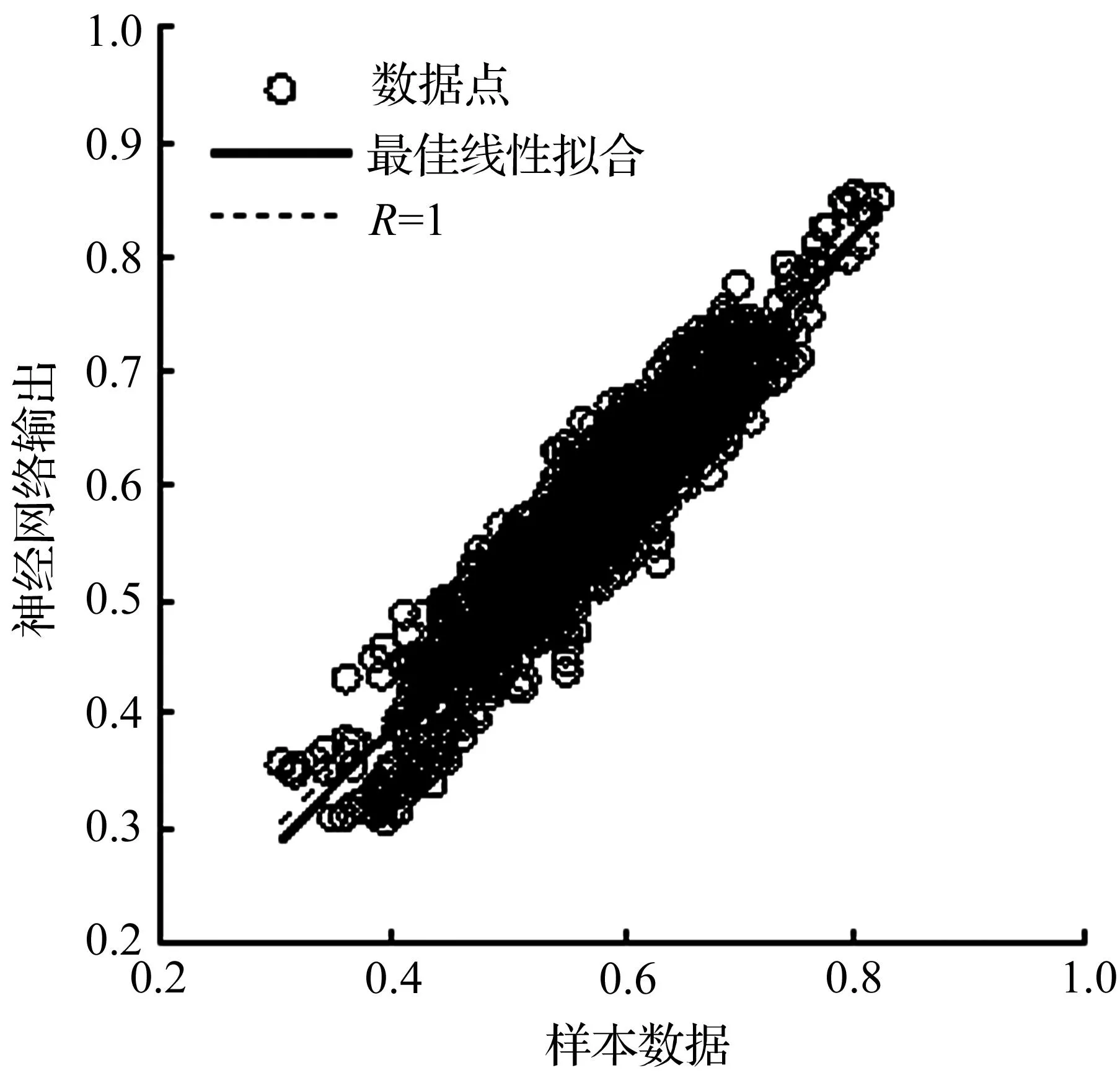
图5相关性比较

Fig.5Correlation comparison

NARX神经网络训练数据的RMSE值为0.018 0，相关性为0.989 1，估计数据的RMSE值为0.028 9，相关性为0.939 5。

为进一步说明本文采用的NARX神经网络的优越性，同时采用BP神经网络进行轨道不平顺的估计，训练算法都采用贝叶斯正则化算法，试验结果如表1所示。从表1可以得到,BP神经网络的训练数据的RMSE为0.058 9，相关性为0.721 1，估计数据的RMSE为0.086 8，相关性为0.641 8。可见采用NARX神经网络，以轴箱垂向振动、构架垂向振动和构架点头角速度为输入估计轨道不平顺优于BP神经网络。

表1　不同神经网络的性能指标

4结论

本文提出了一种基于NARX神经网络的轨道不平顺估计方法。通过建立车辆—轨道垂向耦合动力学仿真模型，以轨道不平顺数据作为输入得到轴箱垂向振动、构架垂向振动和构架点头角速度等仿真信号。将得到的仿真信号作为神经网络的输入，构建以轨道不平顺为输出的神经网络模型。仿真试验结果表明，NARX神经网络模型估计结果的均方根误差为0.028 9，相关系数为0.939 5，优于BP神经网络模型的均方根误差0.086 8和相关系数0.641 8，可见采用NARX神经网络对轨道不平顺进行估计具有较好的效果。

参考文献：

[1]左玉云.铁路轨道不平顺对车轨系统竖向振动响应的影响分析[D]. 长沙：中南大学, 2007.

[2]黄渊旭, 贺德强, 程卫.基于正则化 RBF 的轨道不平顺在线监测系统研究[J]. 广西大学学报(自然科学版), 2014, 39(5): 1007-1013.

[3]RESENDIZ E, HART J M, AHUJA N.Automated visual inspection of railroad tracks[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 751-760.

[4]MONTALBAN DOMINGO M L, MONTROS MONJE J, REAL T, et al.Design and validation of a railway inspection system to detect lateral track geometry defects based on axle-box accelerations registered from in-service trains[J]. Journal of Vibroengineering, 2014, 16(1): 234-248.

[5]朱文发,柴晓冬,郑树彬,等.基于捷联惯性系统的轨道长波不平顺检测[J]. 城市轨道交通研究，2012(11):87-90.

[6]LEE J S, CHOI S, KIM S S, et al.A mixed filtering approach for track condition monitoring using accelerometers on the axle box and bogie[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(3): 749-758.

[7]Li M X D, BERGGREN E G, BERG M, et al.Assessing track geometry quality based on wavelength spectra and track-vehicle dynamic interaction[J]. Vehicle System Dynamics, 2008, 46(S1): 261-276.

[8]宁静,诸昌钤,张兵.基于EMD和Cohen核的轨道不平顺信号分析方法[J]. 振动与冲击，2013(4):31-38.

[9]CAI L, MA S Y, ZHOU Y L.Prediction of SYM-H Index during large storms by NARX neural network from IMF and solar wind data[J]. Annales Geophysicae, 2010, 28:381-393.

[10]张国梁,张志杰,杜红锦,等.基于NARX神经网络的冲击加速度计建模研究[J]. 弹箭与制导学报, 2008, 28(3):284-286.

[11]潘丽莎, 程晓卿, 秦勇, 等.基于 NARX 神经网络的轮重减载率预测[J]. 铁道车辆, 2012, 50(9): 4-7.

[12]HIRSCHEN K, SCHAFER M.Bayesian regularization neural networks for optimizing fluid flow processes[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195:481-500.

[13]ZHAI W, WANG K, CAI C.Fundamentals of vehicle-track coupled dynamics[J]. Vehicle System Dynamics, 2009,47(11):1349-1376.

[14]张媛.某扫雷犁系统的神经网络建模与控制研究[D]. 南京:南京理工大学, 2009.

(责任编辑梁健)

Assessment of vertical track irregularity based on NARX neural network

WANG Gui1, XING Zong-yi1, JIANG Jie2, HUANG Wen2

(1.School of Automation, Nanjing University of Science and Technology, Nanjing 210094 China;2.School of Mechanical Engineering,Nanjing University of Science and Technology, Nanjing 210094 China)

Abstract:Track irregularities are the key factors which influence vehicle stability and safety, it is important to grasp the state of track irregularity for guaranteeing the train operation safety. Due to it is difficult to detected different bands irregularities with a single inertial amount, a method was proposed to assess the vertical track irregularities based on Nonlinear Auto-Regressive with exogenous input Neural Networks(NARX). A coupling dynamics model of vertical vehicle-track interactions was developed with the actual measured track irregularity data from high-speed line as input to obtain the simulation a plurality inertia data. Then, NARX neural network, with the normalization simulation a plurality inertia data as the input and track irregularity as the output, was built to assess vertical track irregularity. The root mean square error (RMSE) and correlation coefficients was applied to evaluate the network performance. Simulation results show that the RMSE of assessed results is 0.028 9, the correlation coefficient is 0.938 7 with NARX neural network model, which is higher than the 0.086 8 and 0.641 8 with Back Propagation (BP) neural network model, respectively. It shows that the proposed method can accurately and efficiently assess the track vertical irregularity.

Key words:track irregularity; online monitoring; NARX neural network; assessment

中图分类号：U216.3

文献标识码：A

文章编号：1001-7445(2016)02-0426-08

doi:10.13624/j.cnki.issn.1001-7445.2016.0426

通讯作者：邢宗义(1974-)，男，山东临沂人，南京理工大学副教授； E-mail:xingzongyi@163.com。

基金项目：国家高科技研究发展计划(863计划)项目(2011AA110501)；中央高校基本科研业务费专项资金项目(30920130132002)

收稿日期：2015-11-30；

修订日期：2016-01-12

引文格式：王贵，邢宗义，蒋杰，等.基于NARX神经网络的轨道垂向不平顺估计[J].广西大学学报(自然科学版)，2016，41(2)：426-433.