基于双剪统一强度理论的垂直井井壁坍塌压力解

崔　莹 ，屈　展，赵均海，王　萍

(1.西安石油大学土木工程系， 陕西西安710065； 2.西北工业大学航空学院， 陕西西安710072；3.长安大学建筑工程学院， 陕西西安710061)



基于双剪统一强度理论的垂直井井壁坍塌压力解

崔莹1,2，屈展1,2，赵均海3，王萍1

(1.西安石油大学土木工程系， 陕西西安710065； 2.西北工业大学航空学院， 陕西西安710072；3.长安大学建筑工程学院， 陕西西安710061)

摘要：针对钻井过程中井壁坍塌压力的理论计算值与实测值存在较大差异的问题，依据井壁力学模型和双剪统一强度理论，通过理论分析和实践验证，推导得出了不考虑渗透作用的垂直井井壁坍塌压力统一解表达式，并分析了不同b值、不同深度、不同强度准则下井壁坍塌压力的变化趋势。结果表明：当井深一定时，随着b值的增大，井壁坍塌压力相应降低。同一b值条件下，随着井深的增加，井壁坍塌压力相应提高。中间主应力对浅层井壁坍塌压力的影响较深层大，中间主应力的引入对井壁岩石强度的提升有着积极作用。文中建立的井壁坍塌压力解公式可以通过改变b值的大小调整中间主应力的贡献，以适应不同地质条件下垂直井井壁的坍塌压力计算。

关键词：双剪统一强度理论；井壁稳定；坍塌压力；中间主应力

0引言

石油天然气钻井过程中的井壁坍塌是常见的井壁稳定问题。为了防止钻井过程中井壁岩石的破坏，需要一定密度的钻井液充满井眼。从力学的角度来说，造成井壁坍塌的主要原因是井内液柱压力较低，使得井壁周围岩石所受应力超过岩石本身的强度而产生剪切破坏所造成的[1]。此外，不同井孔倾斜角、不同地层各向同性面倾斜角也会影响井孔周围的应力分布[2]。因此，计算确定井壁的坍塌压力对确定钻井过程中钻井液密度和保持井壁稳定有着重要的意义。

确定合理的强度准则是计算钻井过程中井壁坍塌压力的前提。目前井壁围岩坍塌压力的计算多基于Mohr-Coulomb强度准则和Drucker-Prager强度准则[3-4]，然而，Mohr-Coulomb强度准则忽略了中间主应力对岩石强度的影响，与实际存在较大差异[5-7]。Drucker-Prager强度准则考虑了中间主应力的影响，但是该准则将中间主应力对岩石强度的贡献夸大，与岩石材料的真三轴试验结果不符，需要对坍塌压力计算结果进行修正[8-10]。国内外学者通过对真三轴试验数据的直接拟合或通过插值、类比方法，建立了许多新的强度准则，但这些准则表达式参数众多且缺乏明确的物理意义，难以应用于实际解析计算[11-17]。因此，井壁坍塌压力计算中合理考虑中间主应力对岩石强度的贡献，以便确定更加符合实际的井壁坍塌压力强度计算准则，仍是钻井过程中井壁稳定评价需要解决的科学问题。俞茂宏教授提出的统一强度理论可以合理地反映中间主应力效应并获得了广泛地应用[18-20]，本文将双剪统一强度理论应用于各向异性应力条件下井壁坍塌压力计算，推导得到了垂直井井壁坍塌压力解表达式，探讨了中间主应力对井壁坍塌压力的影响，并对不同强度准则条件下井壁坍塌压力计算结果的差异进行了比较分析。

1双剪统一强度理论

俞茂宏建立的双剪统一强度理论认为[21]：当作用于双剪单元体上的两个较大切应力及其面上的正应力影响函数达到某一极限值时，材料开始发生破坏。引入岩石力学中剪切强度参数C0和岩石内摩擦角φ，推导得出岩石力学中以压应力为正的主应力形式双剪统一强度理论公式为：

(1a)

(1b)

(2)

式中，σ1为大主应力(MPa)；σ2为中间主应力(MPa)；σ3为小主应力(MPa)。α为材料拉压强度比系数；τ0为材料剪切屈服极限(MPa)；ft为材料拉伸屈服极限(MPa)；fc为材料压缩屈服极限(MPa)；b为反映中主切应力以及相应面上的正应力对材料破坏影响程度的系数，不同的b值可作为选用不同强度理论的参数。

2垂直井井壁坍塌压力统一解表达式

2.1主应力的确定

钻井过程中垂直井井壁围岩通常受到1个上覆岩层压力σv、钻井液液柱压力Pi、2个大小不等的水平地应力σH和σh以及孔隙压力Pp的共同作用。设垂直井半径为r0，以垂直井的中心作为原点，径向坐标为r，井壁上某点的矢径与σH的夹角为环向坐标θ，建立极坐标系。其三维力学模型如图1所示。

假设地层为线弹性多孔材料，井壁围岩处于平面应变状态，依据弹性力学理论，当不考虑地层的渗透作用(即Pp与Pi相互不影响)及应力非线性修正时，井壁围岩应力分布可分别考虑图1中Pi、σH、σh、σv的作用，并依据线性叠加原理叠加得到。简化后井壁平面力学模型如图2所示。依据线性叠加原理，图2可以进一步分解为图3所示。

图1井壁围岩三维力学模型

Fig.1The three-dimensional

mechanic model of wellbore rock

图2井壁围岩平面力学模型

Fig.2The two-dimensional mechanic

model of wellbore rock

+　　+　

以压应力为正，则图3(a)中钻井液液柱压力Pi所引起的围岩应力为：

(3)

同理，可推导出图3(b)中最大水平地应力σH所引起的围岩应力为：

(4)

图3(c)中最小水平地应力σh所引起的围岩应力为：

(5)

设岩石的泊松比为μ，上覆岩层压力σv所引起的围岩应力为：

(6)

在钻井液柱压力和地应力的联合作用下，井壁围岩应力分布可由式(3)～式(6)叠加组成，即：

(7)

式中，Pi为钻井液液柱压力(MPa)；σH为最大水平地应力(MPa)；σh为最小水平地应力(MPa)；σv为上覆岩层压力(MPa)；μ为岩石泊松比。其余符号含义同前。

将r=r0代入式(7)，得垂直井井壁表面的应力分布表达式为：

(8)

在式(8)的基础上考虑围岩孔隙压力Pp的作用，则垂直井井壁围岩的有效应力分布可以表达为：

(9)

式中，ξ为有效应力系数；Pp为孔隙压力(MPa)。其余符号含义同前。

(10)

对于岩石剪切破坏的情况，考虑式(10)得主应力表达式为：

(11)

2.2垂直井井壁坍塌压力统一解表达式

(12)

其中，A=1-sinφ，B=1-sinφ-2μ-2μsinφ。

3井壁坍塌压力计算的探讨

3.1实例分析

以克拉玛依油田呼2井安集海河组为例，其相关地质参数资料如下[1]：

井段范围H=2 900～2 940 m；地应力梯度：σH=2.73 MPa/100 m，σh=1.82 MPa/100 m，σv=2.34 MPa/100 m；地层孔隙压力系数pp=1.2；有效应力系数ξ=0.4；泊松比μ=0.2；岩石强度参数：C0=11.08 MPa，φ=19.8°。

为了考察中间主应力对井壁坍塌压力的影响，将上述具体参数代入式(12)，讨论仅中间主应力不同条件下不同井段深度处坍塌压力变化情况。为了便于比较，将计算得到的该深度处井壁坍塌压力折算成当量钻井液密度进行分析。

令b分别为0、0.25、0.50、0.75、1.00所得出的不同井深条件下坍塌压力(当量钻井液密度)变化曲线如图4所示。从图4中的曲线变化情况可以看出，不同b值条件下坍塌压力(当量钻井液密度)随着井深的不断增加均相应增长，同时，深度在1 000 m以内钻井液密度上升较快，之后趋于平缓。在同一深度处钻井液密度随着b值的增加而相应降低，即考虑中间主应力作用的围岩强度较高，井壁坍塌压力较低，低密度钻井液即可满足井壁稳定要求。随着深度的不断增加，同一深度处不同b值的当量钻井液密度之间的差异由最大的62.5%降低至12.6%，说明不同中间主应力参数条件对浅层井壁坍塌压力的影响较大，随着井深的不断增加，不同中间主应力参数所确定的井壁坍塌压力差异降低。

图4　不同b值条件下不同深度坍塌压力(当量钻井液密度)变化曲线

依据测井资料，呼2井在H=2 900～2 940 m井段实际确定的井壁稳定液柱压力临界值，即坍塌压力的当量钻井液密度变化范围为1.75～1.80 g/cm3。将不同b值条件下该井段深度处坍塌压力的当量钻井液密度变化范围计算结果与实际值进行比较，结果如表1所示。

从表1中的数据比较可以看出，随着中间主应力贡献的不断加大，该井段范围内坍塌压力当量钻井液密度计算值与依据测井资料确定的实际值误差逐步减小。从计算结果来看，b=1时计算值与实际值误差在6%以内，即针对呼2井该井段的实际地质情况，式(12)应采用双剪强度理论(即b=1)计算井壁坍塌压力较为合理。

表1　不同b值条件下同一井段井壁坍塌压力(当量钻井液密度)计算值与实际值对比

3.2不同强度理论条件下井壁坍塌压力的分析

3.2.1不同强度理论条件下同一井深处井壁坍塌压力的计算

依据前述分析结果，分别选择Mohr-Coulomb强度准则、Drucker-Prager强度准则和本文推导的统一解公式(令b=1)，计算井深H=2 940处井壁坍塌压力值。

①Mohr-Coulomb强度准则

Mohr-Coulomb强度准则仅考虑了大主应力和小主应力对材料强度的影响，当不考虑围岩应力非线性修正时，垂直井井壁坍塌压力的计算公式为：

(13)

将上述垂直井参数代入式(13)中，可以得到Mohr-Coulomb强度准则下该深度处井壁坍塌压力的当量钻井液密度为1.905 g/cm3。

②Drucker-Prager强度准则

Drucker-Prager强度准则中考虑了3个主应力对材料强度的影响，当不考虑围岩应力非线性修正时，垂直井井壁坍塌压力的计算公式为：

(14)

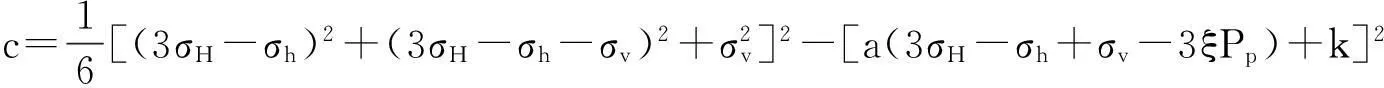
(15)

式(15)中的参数a和k为与岩石强度参数C0和φ相关的参数，按照偏平面与Mohr-Coulomb准则的关系可以得出，即：

(16)

(17)

将上述垂直井参数代入式(14)～式(17)中，可以得到Drucker-Prager强度准则下该深度处井壁坍塌压力的当量钻井液密度为1.587 g/cm3。

③双剪强度理论

将本文推导出来的井壁坍塌压力统一解表达式(12)中的反映中主切应力以及相应面上的正应力对材料破坏影响程度的系数b取为1，即得到双剪强度理论下不考虑地层渗透作用及应力非线性修正时垂直井井壁坍塌压力的计算公式为：

(18)

将上述垂直井参数代入式(18)中，可以得到双剪强度理论下该深度处井壁坍塌压力的当量钻井液密度为1.857 g/cm3。

依据测井资料，呼2井在该深度井段实际确定的井壁稳定液柱压力临界值，即坍塌压力的当量钻井液密度为1.80 g/cm3。将三种强度理论下针对呼2井该深度井段计算确定的坍塌压力当量钻井液密度值与实际值进行比较，结果见表2。

从计算结果可以看出，针对同一井段深度及围岩地质条件，Mohr-Coulomb强度准则计算的坍塌压力最大，Drucker-Prager强度准则计算的坍塌压力最小，双剪强度理论计算的坍塌压力居中。这是由于Mohr-Coulomb强度准则中没有考虑中间主应力的影响，从而使计算得出的维持井壁稳定所需的钻井液密度偏于保守，而Drucker-Prager强度准则中对中间主应力对强度的贡献考虑过大，使计算得出的维持井壁稳定所需的钻井液密度偏于危险。从表2中计算值与实际值的比较可以发现，应用本文所推导理论公式(18)的计算结果与实际值的误差在5%以内，表明双剪强度理论合理考虑中间主应力对岩石强度的贡献，更切近实际。

表2　不同强度理论下井壁坍塌压力(当量钻井液密度)计算值

3.2.2不同强度理论条件下坍塌压力(当量钻井液密度)随油井深度的变化情况

为考察不同强度理论条件下井壁坍塌压力随深度的变化情况，分别按照Mohr-Coulomb强度准则、Drucker-Prager强度准则和双剪强度理论计算得到的不同井深条件下坍塌压力(当量钻井液密度)变化曲线如图5所示。从图5曲线的变化可以看出，随着井深的不断增加，不同强度理论计算得出的钻井液密度均相应增加，其变化规律一致，表明在坍塌压力的计算上均具有一定的适应性。从3条曲线的分布来看，同一深度处，Mohr-Coulomb强度准则所计算得到的当量钻井液密度最大，Drucker-Prager强度准则的最小，双剪强度理论的结果居中，表明双剪强度理论计算得到的坍塌压力由于合理考虑了中间主应力对岩石强度的贡献，更加趋于合理。从3条曲线的关系还可以看出，双剪强度理论计算得到的钻井液密度在深度较小处接近Drucker-Prager强度理论的计算结果，在深度较大处接近Mohr-Coulomb强度理论的计算结果，这一结果表明中间主应力对井壁浅层围岩强度的影响较深层要大。

图5　不同强度准则下坍塌压力(当量钻井液密度)随井深的变化曲线

4结论

通过应用双剪统一强度理论推导垂直井井壁坍塌压力统一解表达式并进行分析，可以得出如下结论：

①随着油井深度的增加，井壁坍塌压力相应增加，在同一深度处井壁坍塌压力随着井壁围岩中间主应力贡献的增加而相应降低。

②中间主应力对浅层井壁坍塌压力值的影响较大。随着井深的不断增加，不同中间主应力参数条件下的井壁坍塌压力差异逐渐降低。

③考虑中间主应力可以充分发挥围岩的强度储备，从而降低钻井液密度，这为工程上低密度钻井液的应用提供了理论支持，但应当合理考虑中间主应力对井壁围岩强度的贡献，过高估计中间主应力的作用也是不合理的。

④应用双剪统一强度理论推导得到的垂直井井壁坍塌压力计算表达式有较好的涵盖性，通过改变参数b值的大小可以调整中间主应力的贡献，以适应不同地质资料钻井井壁的坍塌压力计算。

参考文献:

[1]邓金根,程远方,陈勉,等.井壁稳定预测技术[M]. 北京：石油工业出版社, 2008.

[2]邸元,袁子峰.倾斜地层中斜井井孔的应力分析[J]. 地下空间与工程学报, 2012, 8(5) : 981-988.

[3]梁涛,杨甘生,雷静.中间主应力对垂直井井壁坍塌压力的影响[J]. 探矿工程, 2012, 39(4) : 11-15.

[4]李玉伟,艾池,王志成,等.深井安全钻井液密度窗口影响因素[J]. 油气地质与采收率, 2013, 20(1) : 107-110.

[5]HAIMSON B C, CHANG C.A new true triaxial cell for testing mechanical properties of rock and its use to determine rock strength and deformability of Westerly granite[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 37(1):285-296.

[6]HAIMSON B C, CHANG C.True triaxial strength of the KTB amphibolite under borehole wall conditions and its use to estimate the maximum horizontal in-situ stress[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B10):2257-2271.

[7]刘玉石.地层坍塌压力及井壁稳定对策研究[J]. 岩石力学与工程学报, 2004, 23(14): 2421-2423.

[8]李天太,孙正义.井壁失稳判断准则及应用分析[J]. 西安石油学院学报(自然科学版), 2002, 17(5) : 25-27.

[9]邱康,陈勉,金衍.基于统计损伤的井壁坍塌压力模型[J]. 岩土力学, 2011, 32(7) : 2029-2033.

[10]周凤玺，李世荣.广义Drucker-Prager强度准则[J]. 岩土力学, 2008,29(3):747-751.

[11]AL-AJMI A M, ZIMMERMAN R W.Relationship between the parameters of the Mogi and Coulomb failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3):431-439.

[12]AL-AJMI A M , ZIMMERMAN R W.Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(8):1200-1211.

[13]COSTAMAGNA R, BRUHNS O T.A four-parameter criterion for failure of geomaterials[J]. Engineering Structures, 2007, 29(3):461-468.

[14]MORTARA G.A new yield and failure criterion for geomaterials[J]. Geotechnique, 2008, 58(2): 125-132.

[15]陈景涛,冯夏庭.高地应力下硬岩的本构模型研究[J]. 岩土力学, 2007, 28(11):2271-2278.

[16]姚仰平,路德春,周安楠,等.广义非线性强度理论及其变换应力空间[J]. 中国科学(E辑),2004,34(11):1283-1299.

[17]周小平,钱七虎,杨海清.深部岩体强度准则[J]. 岩石力学与工程学报, 2008, 27(1):117-123.

[18]赵均海,李艳,张常光,等.基于统一强度理论的石油套管柱抗挤强度[J]. 石油学报, 2013, 34(5) : 969-976.

[19]崔莹,赵均海,张常光,等.基于统一强度理论的灰土桩复合地基挤密影响区半径计算[J]. 岩土力学, 2013,34(4):1116-1120.

[20]赵均海,崔莹,张常光,等.灰土挤密复合地基桩体极限承载力统一解[J]. 广西大学学报(自然科学版), 2013,38(1):125-131.

[21]YU Mao-hong.Unified Strength Theory and its applications[M]. Germany: Springer-verlag Berlin Heidelberg, 2004.

(责任编辑唐汉民裴润梅)

Collapse pressure solution of vertical wellbore based on twin-shear unified strength theory

CUI Ying1, 2，QU Zhan1, 2，ZHAO Jun-hai3，WANG Ping1

(1.Department of Civil Engineering, Xi’an Shiyou University, Xi’an 710065, China;2.School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China;3.School of Civil Engineering, Chang’an University, Xi’an 710061, China)

Abstract：As the theoretical values for collapse pressure of vertical wellbore were quite different from the actual measured values, based on the twin-shear unified strength theory and the mechanical model of wellbore rock, a computational method for collapse pressure of vertical wellbore without considering the penetration of wellbore was analyzed and discussed. The unified formula of the collapse pressure was deduced and proved by analyzing the different factors, such as different b values, different depths of wellbore and different strength criteria. The results show that, under the condition of wellbore depth being unchanged, the collapse pressure decreases with the increase of b value. Also, under the condition of b value being unchanged, the collapse pressure increases with the increase of wellbore depth. The results also show the intermediate principal stress has greater impact on the collapse pressure of shallow borehole than that of deep one. And the deduced solution considering the intermediate principal stress has active meaning to the ultimate strength of rock. The proposed unified formula of the collapse pressure based on the twin-shear unified strength theory can meet different geological conditions by changing the value of b.

Key words：twin shear unified strength theory; wellbore stability; collapse pressure; intermediate principal stress

中图分类号：TU452

文献标识码：A

文章编号：1001-7445(2016)02-0346-09

doi:10.13624/j.cnki.issn.1001-7445.2016.0346

通讯作者：崔莹(1979—)，男，陕西西安人，西安石油大学讲师，博士；E-mail: cuiying126@163.com。

基金项目：国家自然科学基金资助项目(51174162)；陕西省教育厅专项科研计划项目(15JK1561)；西安石油大学青年科技创新基金项目(2015BS17)

收稿日期：2015-12-28；

修订日期：2016-01-21

引文格式：崔莹，屈展，赵均海，等.基于双剪统一强度理论的垂直井井壁坍塌压力解[J].广西大学学报(自然科学版)，2016，41(2)：346-354.