基于三参数强度准则的高强混凝土井壁力学特性分析

李雪梅，荣传新，程　桦

(安徽理工大学土木建筑学院， 安徽淮南232001)



基于三参数强度准则的高强混凝土井壁力学特性分析

李雪梅，荣传新，程桦

(安徽理工大学土木建筑学院， 安徽淮南232001)

摘要：为了分析高强混凝土井壁的力学特性，采用三参数强度准则推导出了高强混凝土立井井壁极限承载力理论解以及弹性区和塑性区应力与半径和荷载之间的解析表达式，并对计算结果进行了实验的验证。计算分析表明：在弹性区，高强混凝土井壁径向压应力σr随半径r的增大而增大，环向压应力σ(θ)随半径r的增大而减少；在塑性区，径向压应力σr和环向压应力σ(θ)均随半径r的增大而增大。当井壁内半径为4.0 m、厚度为1.0 m、混凝土强度等级为C60时，井壁极限承载力为22.87 MPa，井壁厚度每增加0.1 m，井壁极限承载力增加2.8 MPa左右。同时，混凝土井壁的环向压应力σ(θ)达到164.38 MPa，是混凝土立方体单轴抗压强度的2.7倍左右，表明考虑了混凝土多轴强度影响的三参数强度准则更适用于高强混凝土井壁力学特性分析，为高强混凝土井壁结构的设计计算提供了的理论参考。

关键词：三参数强度准则；高强混凝土井壁；极限承载力；井壁应力

因浅部煤炭资源的日益枯竭，在山东和安徽等产煤大省的煤炭开发已逐渐转向深部，新井建设时煤矿立井井筒需要穿过的冲积层越来越厚，如在建的山东巨野煤田万福矿和即将建设安徽展沟煤田口孜西矿井穿过的第三和第四系表土层达600～800 m。在如此深厚的冲积层中建井必须大幅度提高立井井壁极限承载力，以抵抗作用在其上巨大的水土压力，为此，在井壁结构设计中采用了C60～C80的高强混凝土。关于混凝土井壁结构的研究已有较多的报道[1-4]，但关于高强混凝土井壁结构的力学特性研究多以实验研究为主[5-8]，并根据井壁模型实验结果得到了井壁极限承载力的实验回归公式，同时采用Mohr-Coulomb准则分析了井壁结构的力学特性[9]。在压力不太大的情况下，采用Mohr-Coulomb准则对其进行分析是比较符合实际，但当压力较大的情况下则采用三参数强度准则[10-11]能更好地反映高强混凝土井壁的力学特性，因为该准则考虑了混凝土在多轴应力下的力学性能[12]。深厚冲积层冻结法施工的煤矿立井井壁一般采用双层井壁结构型式，冻结井内层井壁中的混凝土一般处于双向或三向应力状态[13]。本文针对深冻结井内层井壁受力特点，采用了符合混凝土强度特性的三参数强度准则[14]，通过分析计算，推导出高强混凝土立井井壁结构极限承载力以及井壁弹性区和塑性区应力的解析表达式，旨在为井壁的结构设计提供更多的理论参考。

1混凝土三参数强度准则

三参数强度准则的破坏面为外凸的光滑曲面，其子午线为抛物线，在负静水压力轴的方向是开口的，描述准则的三个力学特征值为单轴抗拉强度σl、单轴抗压强度σy、双轴抗压强度σ2y[10]，三参数准则通常以ρ、ξ、θ表示其应力组合，其中：

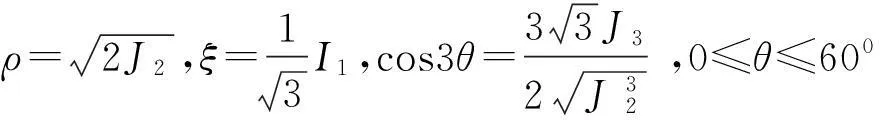
(1)

式中：

I1=σ1+σ2+σ3=3σm，

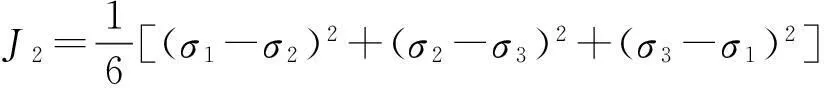
J3=s1s2s3=(σ1-σm)(σ2-σm)(σ3-σm)。

三参数强度准则的屈服面如图1所示，破坏面上任一点M(ρ,ξ,θ)满足：

M(ρ,ξ,θ)=ρ2+A1(θ)ρ+A2(θ)ξ+A3(θ)=0，

(2)

式中：

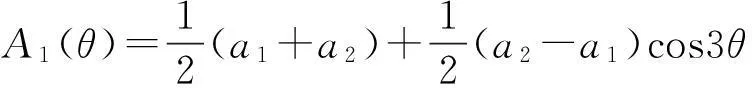
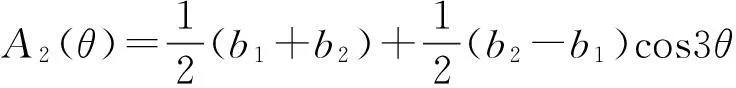
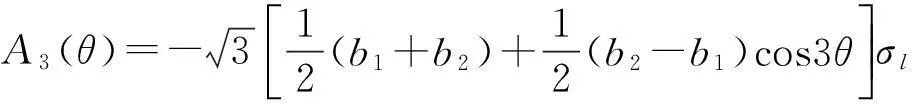
其中：

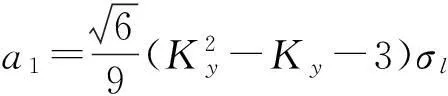
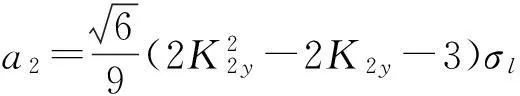
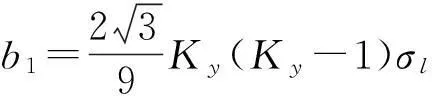
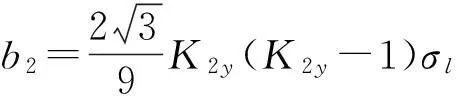
Ky=σy/σl，

K2y=σ2y/σl。

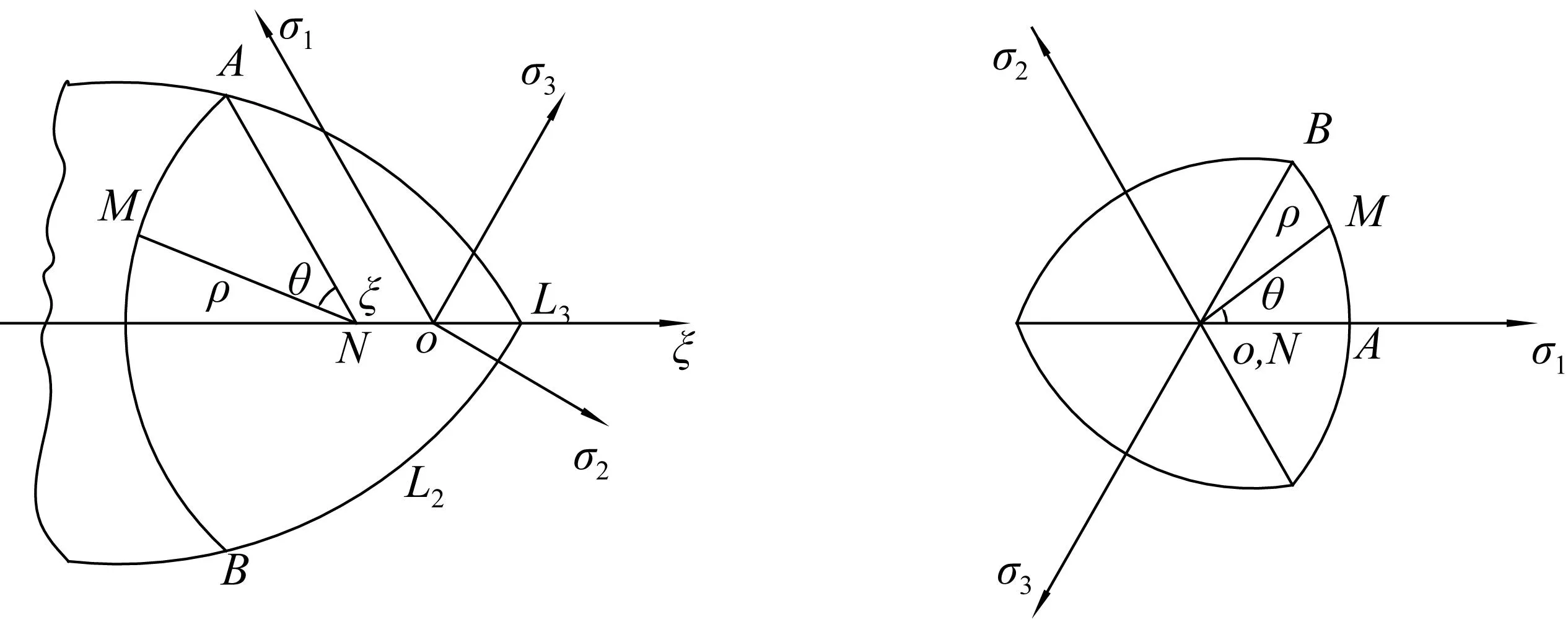
图1　三参数强度准则

2高强混凝土井壁结构力学特性分析

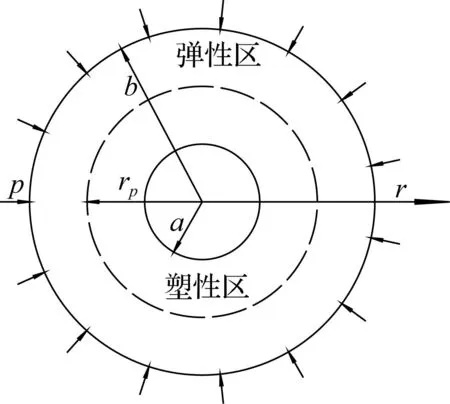
图2　高强混凝土井壁的力学模型Fig.2　Mechanical model of high-strength concrete shaft lining

混凝土井壁在外压作用下，其应力分量σr，σθ,σz为主应力，且有σr>σz>σθ，σr<0，σθ<0。井筒的径向和轴向应力均为压应力。设煤矿立井井筒的内半径为a，外半径为b，在外压作用下井壁处于弹塑性状态，弹塑性分界半径为rp，如图2所示。

主应力符号规定，拉为“+”、压为“-”，且σ1>σ2>σ3。

2.1三参数准则应用于井壁极限承载力分析中的公式推导

煤矿立井井壁可以作为平面轴对称问题进行分析，径向应力和切向应力仅是r的函数，与θ无关，σr=σr(r)，σθ=σθ(r)。假设中间主应力为σz=β(σr+σθ)/2，0≤β≤1，β为中间主应力系数，在井壁塑性区，取β=1 ，则σ1=σr，σ3=σθ，σ2=(σr+σθ)/2，从而有：

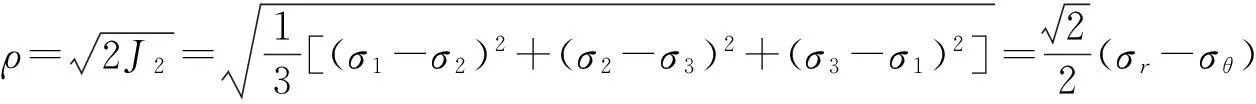
(3)

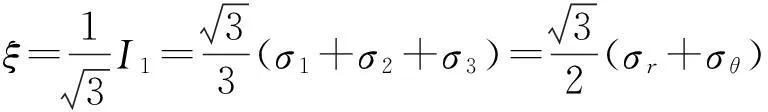
(4)

cos3θ=0，

(5)

由式(3)和式(4)可得：

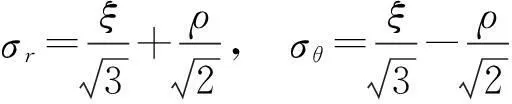
(6)

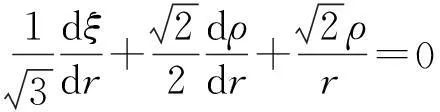
(7)

将式(5)代入式(2)，得：

ρ2+C1ρ+C2ξ+C3=0，

(8)

因此，求解混凝土井壁受外压p作用的问题时应满足平衡条件式(7)、强度准则式(8)以及边界条件：

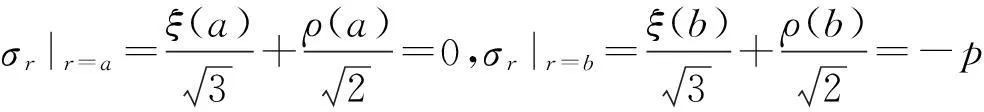
当p很小时，整个立井井筒处于线弹性阶段，各应力分量为：

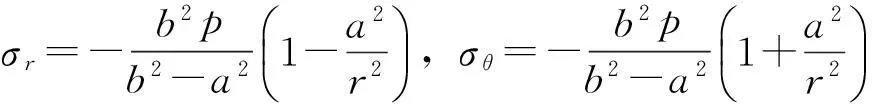
代入式(3)和式(4)，可得：

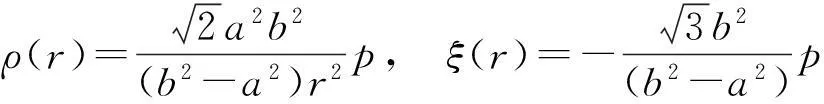
(9)

将式(9)代入强度条件式(8)，可得：

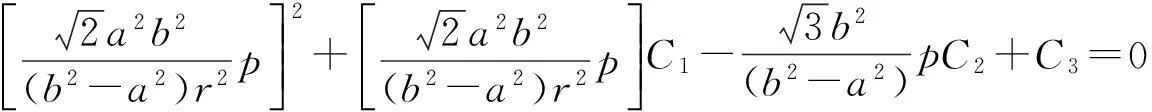
(10)

由此可知，当外压p逐渐增大时，井筒内壁(r=a)最先满足强度条件(或称进入塑性)，相应的外压为弹性极限压力，记为pe。把r=a代入式(10)，可得：

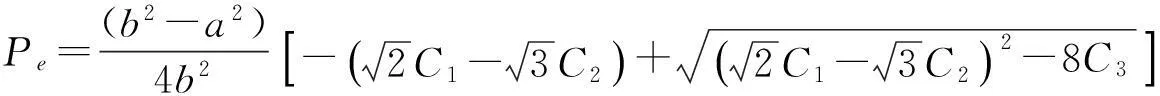
(11)

当p>pe时，在井壁内缘出现塑性区(a≤r≤rp)，并且随着荷载p的增加，塑性区逐渐向外扩展。若弹塑性分界半径为rp，由于轴对称，在交界面上只能有径向压力q，即σr|r=rp=-q。在塑性区内，应力分量应满足平衡方程与强度准则。对于混凝土，有Ky≫1和K2y≫1，因此，有C2>0，由式(8)可得：

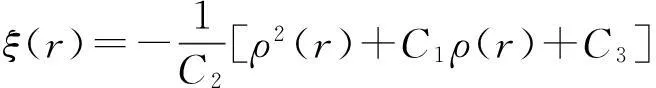
(12)

将式(12)代入式(7)，有：

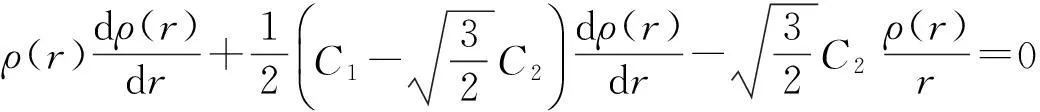
(13)

将式(13)积分，并利用边界条件σr|r=a=0，整理可得：

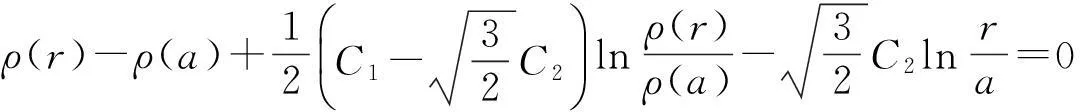
(14)

把式(11)和r=a代入式(9)第一式，可得：

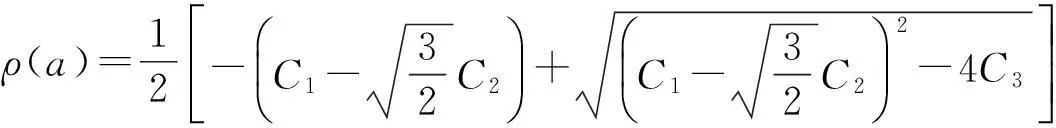
(15)

把C1、C2和C3的值代入式(15)得到ρ(a)，同时联立式(14)、式(12)和式(6)可确定塑性区内的应力分量为：

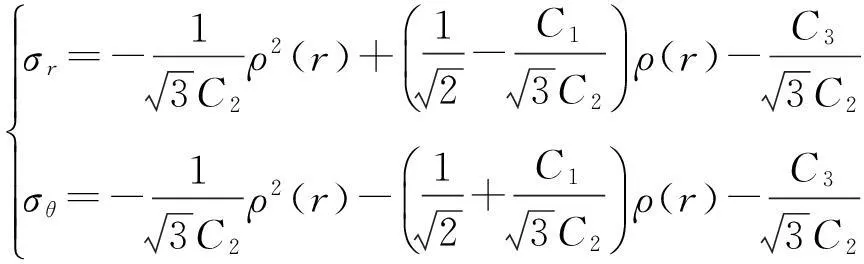
(16)

式中，ρ(r)可根据式(14)在代入各参数后利用MATLAB求得，其余参数同前。

当混凝土立井井筒出现塑性区时，在弹性区(rp≤r≤b)内可视为在r=rp处受内压q作用，在r=b处受外压p作用的弹性混凝土立井井筒，其应力分量为：

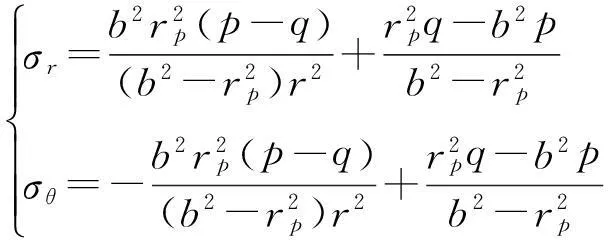
(17)

将式(17)代入(3)和式(4)，有：

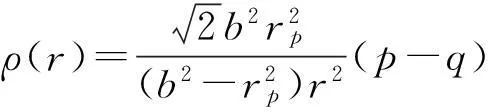
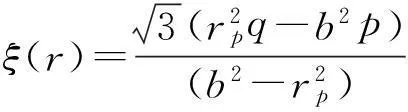
在r=rp处，有：

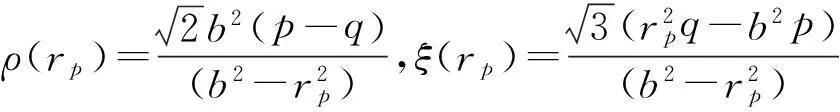
(18)

式(18)中q和rp均未知，可以由弹性与塑性交界处径向应力相等的条件确定二者之间的关系。在塑性区r=rp处求σr时，利用式(6)第一式及式(12)，有：

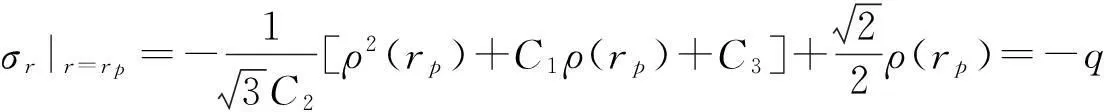
(19)

在弹性区的r=rp处，材料刚进入塑性状态，应力分量应满足强度准则，将式(18)代入(8)式，可得：

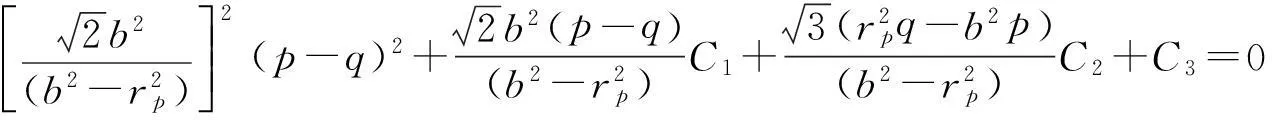
(20)

把r=rp和ρ(a)的值代入式(14)得ρ(rp)，再联立式(19)和式(20)得井壁极限承载力pp与塑性区半径rp的关系式为：

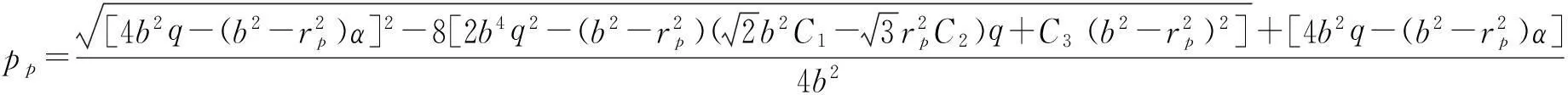
(21)

2.2理论计算与模型实验结果对比分析

由文献[9]中高强钢筋混凝土井壁结构实验结果可知，把模型实验的参数代入式(21)，此时rp=b，得到的高强混凝土井壁极限承载力如表1所示。由表1可知，计算结果和实验结果相差很小，其误差在±5.0%左右，表明三参数强度准则不仅参数少、函数形式简单，由此推导出的理论计算公式能够很好地反映高强混凝土井壁结构的力学特性。

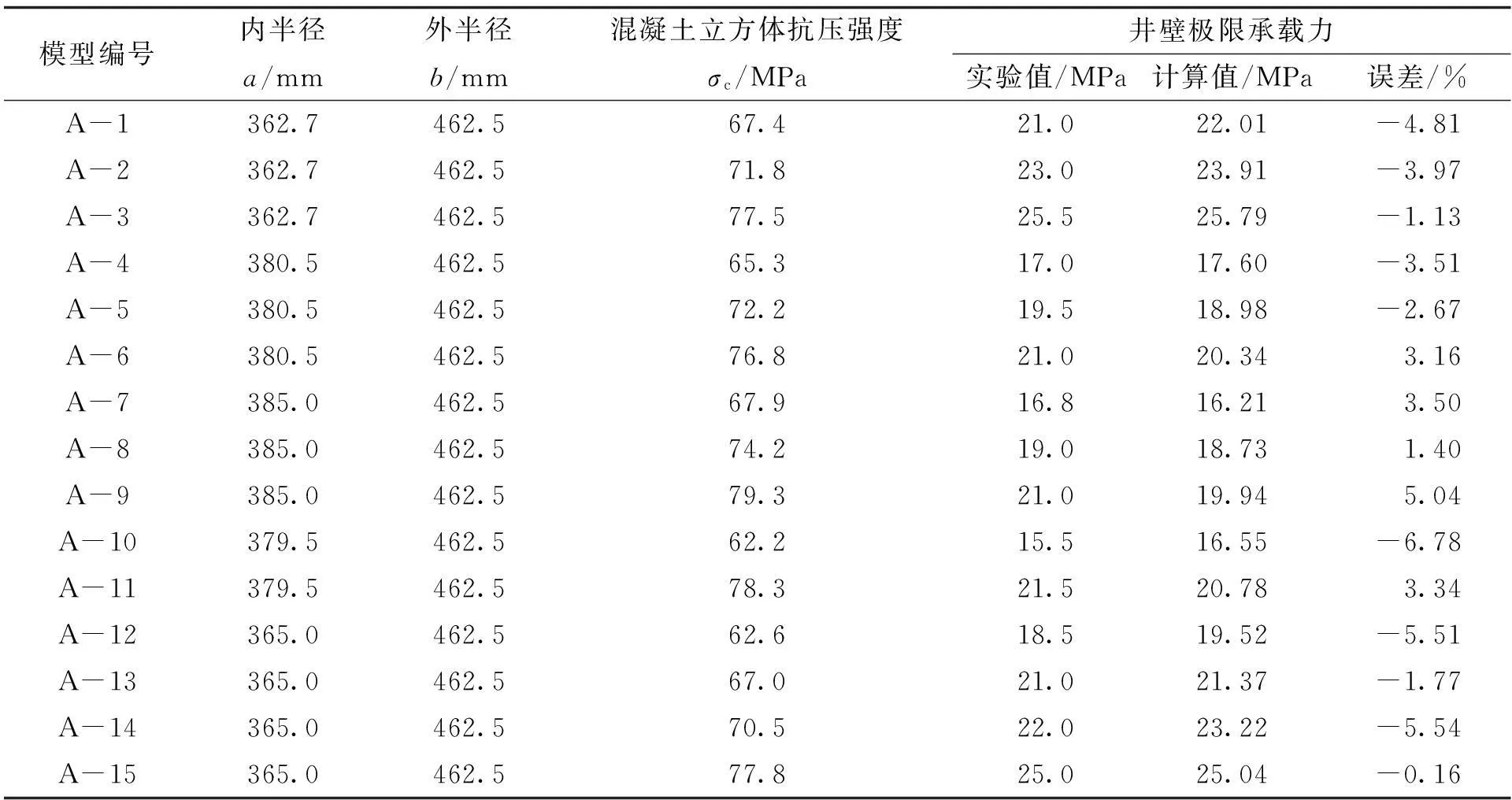
表1　混凝土井壁塑性极限承载力理论分析与实验结果的比较

2.3井壁极限承载力分析

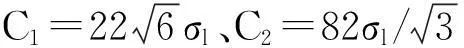
以C60混凝土为例，井壁内半径a=4.0 m，外半径b分别取4.8 m、4.9 m、5.0 m、5.1 m，5.2 m时，几何尺寸的大小对井壁极限承载力的影响如表3和图4所示。表3中，每个塑性区半径所在列的第一个数据为每个半径所对应的井壁塑性极限承载力。由表3和图4可见，不同厚度的井壁在同一塑性区半径处的极限承载力相差很大，且井壁厚度每增加0.1 m，井壁的塑性极限承载力增加2.8 MPa左右。

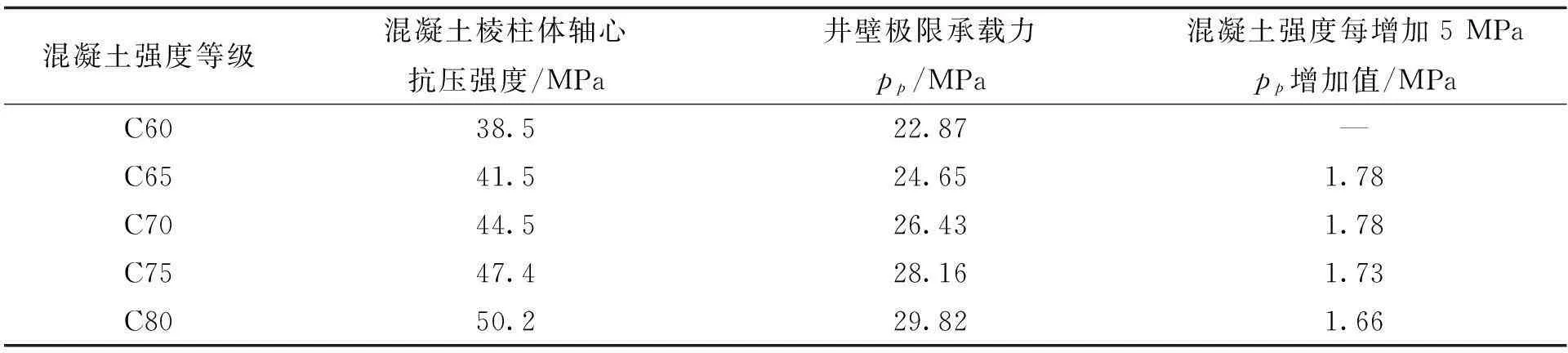
表2　不同强度等级的混凝土所对应的井壁极限承载力分析

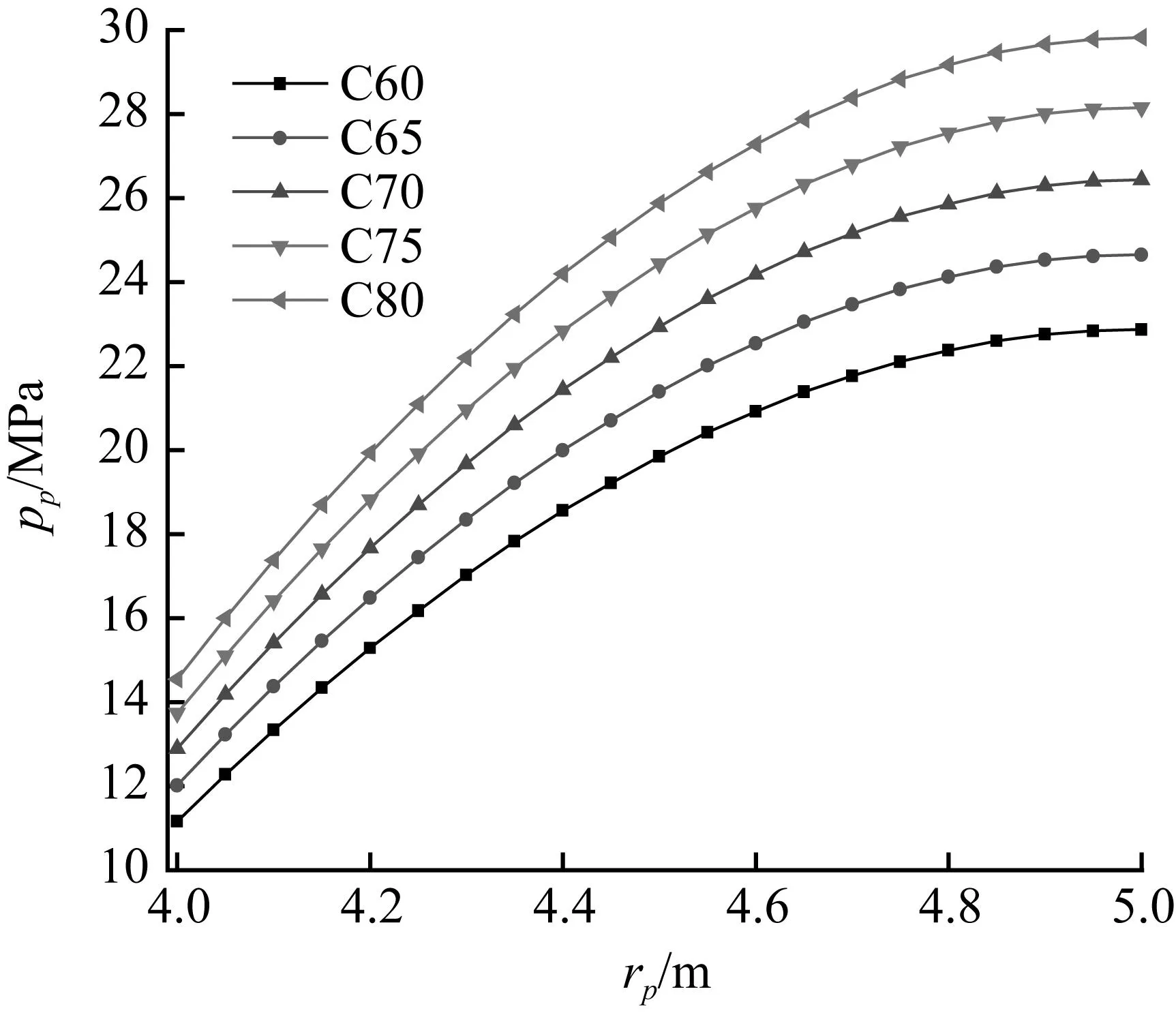
图3　强度等级不同时，极限承载力pp与

塑性区半径rp的关系曲线图

Fig.3Curve of ultimate bearing capacityppand

plastic radiusrpunder different concrete strength

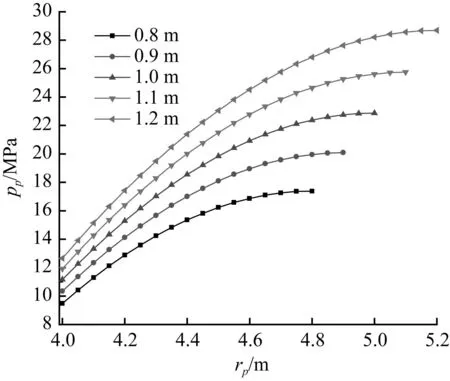
图4井壁厚度不同时，极限承载力pp与

塑性区半径rp的关系曲线图

Fig.4Curve of ultimate bearing capacityppand plastic

radiusrpunder different thickness of the shaft lining

表3井壁厚度不同时，不同位置所对应的井壁极限承载力分析

Tab.3The analysis of ultimate bearing capacity of shaft liningpp, when different thickness of the shaft lining

混凝土井壁厚度/m井壁极限承载力/MParp=4.8mrp=4.9mrp=5.0mrp=5.1mrp=5.2m厚度每增加0.1m承载力变化值0.817.38—————0.919.9520.09———2.711.022.3822.7522.87——2.781.124.6625.2625.6125.75—2.881.226.8127.6328.2028.5828.692.94

2.4井壁应力分析

取井壁内半径a=4 m，外半径b=5 m，混凝土强度等级为C60。当井壁的塑性区半径rp=4.0 m时，对应井壁的弹性极限承载力为11.16 MPa；rp=4.3 m时，井壁极限承载力为17.02 MPa；rp=4.5 m时，井壁极限承载力为19.85 MPa；rp=5.0 m时，对应井壁的极限承载力为22.87 MPa。井壁外围分别承受这四种荷载作用下，井壁应力σr、σθ和半径r的关系曲线如图5和图6所示。由此可见，在弹性区，径向压应力σr随半径r的增大而增大，环向压应力σθ随半径r的增大而减少，均呈抛物线性分布；在塑性区，压应力σr、σθ均随半径r的增大而增大。当高强混凝土井壁的极限承载力等于22.87 MPa时，由于考虑了混凝土多轴强度的影响，混凝土井壁的环向压应力σθ达到了164.38 MPa，是混凝土立方体单轴抗压强度的2.7倍左右。

取r的值分别为4.3 m、4.5 m、4.7 m和5.0 m(记为r1)，计算并绘出不同位置处压应力σr、σθ和荷载Pp的关系曲线如图7和图8所示。结果表明，随着荷载的增大，处于弹性区(a≤r≤r1)的井壁混凝土压应力σr、σθ逐渐增加，而当荷载增加达到塑性半径所对应的极限荷载后，该位置的井壁混凝土径向和环向应力则保持不变，表明混凝土塑性区应力仅与塑性半径rp和混凝土本身的性能有关。当荷载为17.02 MPa时，井壁的塑性区半径rp=4.3 m，径向应力σr为-5.48 MPa，环向应力σθ为-94.18 MPa，但随着荷载的增大，在r=4.3 m处，井壁混凝土径向和环向应力均保持不变。

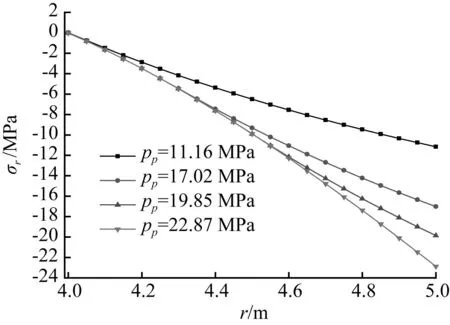
图5pp取不同值时，径向应力σr

与半径r的关系曲线图

Fig.5Curve of radial stressσrand

radiusr, when differentppvalue

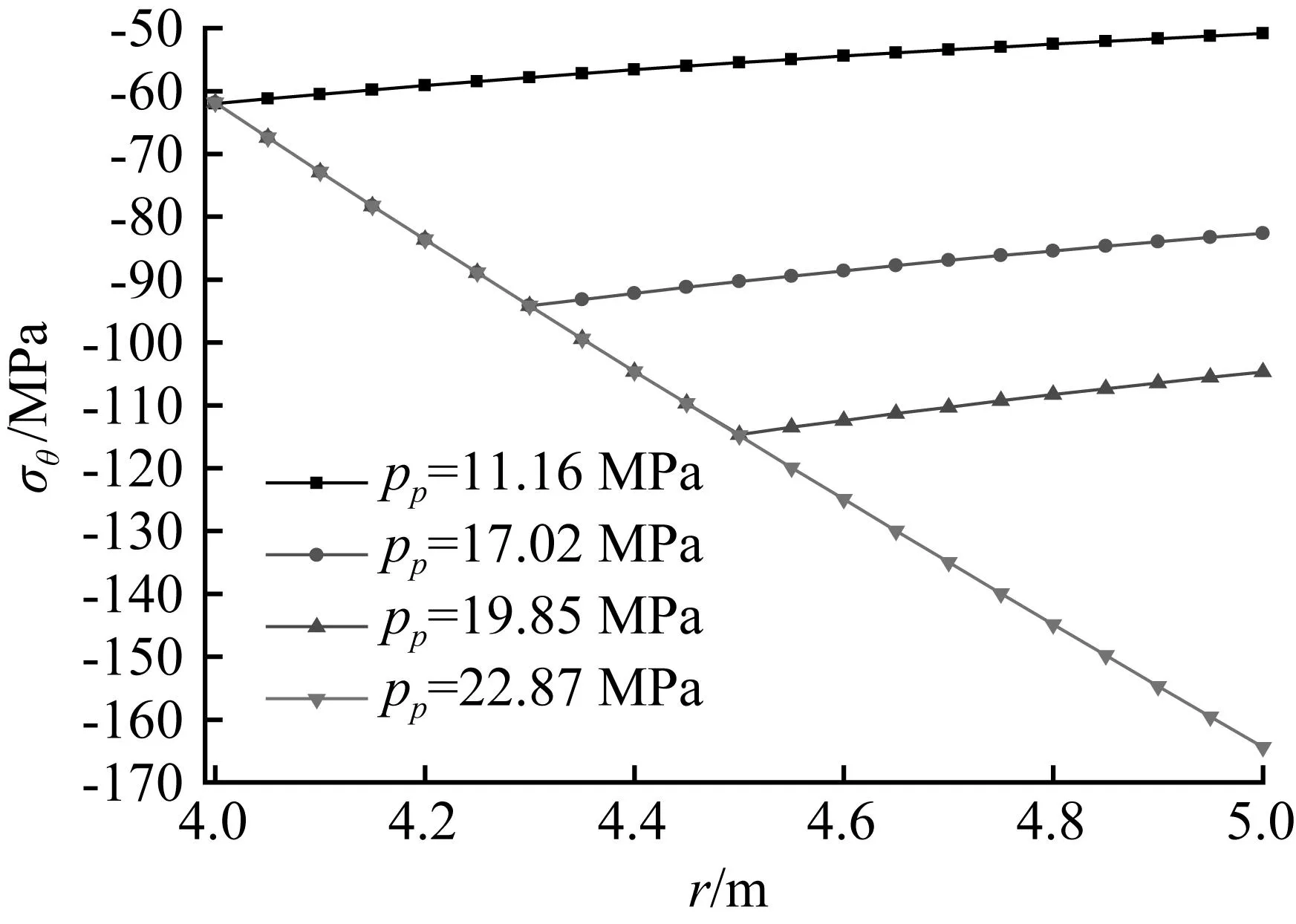
图6pp取不同值时，环向应力σθ

与半径r的关系曲线图

Fig.6Curve of hoop stressσθand

radiusr, when differentppvalue

图7r取不同值时，径向应力σr和

荷载p的关系曲线图

Fig.7Curve of radial stressσrand

loadp, when different r value

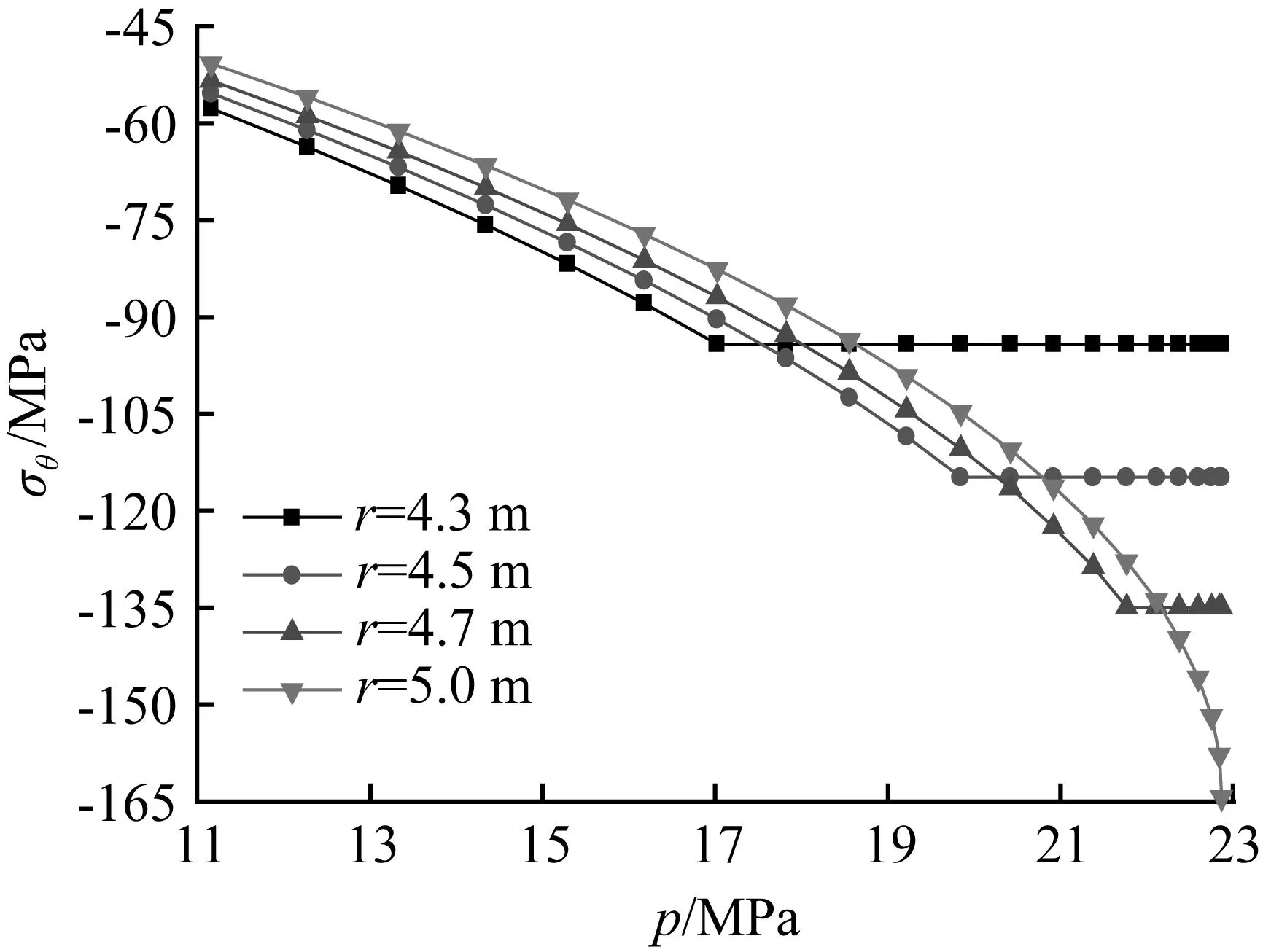
图8r取不同值时，环向应力σθ和

荷载p的关系曲线图

Fig.8Curve of hoop stressσθand

loadp, when differentrvalue

综上所述，高强混凝土立井井壁结构的压应力σr、σθ在塑性区(a≤r≤rp)仅和半径有关，在弹性区(rp≤r≤b)除了和半径有关外还与所受荷载有关。由于三参数强度准则考虑了混凝土多轴强度的影响，极大地提高了高强混凝土井壁的环向应力，且实验结果也表明三参数强度准则用于高强混凝土井壁力学特性的分析是安全可靠的。

3结论

①文中基于三参数强度准则推导出了高强混凝土井壁极限承载力理论解，以及弹性区和塑性区应力与半径和荷载之间的解析表达式。高强混凝土井壁极限承载力计算结果和实验结果相差很小，其误差均在±5.0%左右。由此可见，采用三参数强度准则对高强混凝土井壁结构进行力学特性分析是可行的。

②凝土强度等级和几何尺寸对井壁极限承载力的影响较大，当井壁内半径为4.0 m、井壁厚度为1.0 m、混凝土强度等级为C60时，井壁极限承载力为22.87 MPa；井壁厚度每增加0.1 m，井壁极限承载力增加2.8 MPa左右。同时，混凝土井壁的环向压应力σθ达到164.38 MPa，是混凝土立方体单轴抗压强度的2.7倍左右，表明三参数强度准则更适用于高强混凝土井壁力学特性分析。另外，井壁混凝土强度等级从C60至C80每提高5 MPa，井壁极限承载力增加1.7 MPa左右。

③弹性区，高强混凝土井壁径向压应力σr随半径r的增大而增大，环向压应力σθ随半径r的增大而减少，均呈抛物线性分布；在塑性区，径向压应力σr和环向压应力σθ均随半径r的增大而增大。由此可见，井壁结构的应力σr、σθ在塑性区(a≤r≤rp)仅与半径有关，在弹性区(rp≤r≤b)不仅与半径有关外，而且还与外荷载有关。

参考文献：

[1]姚直书，桂建刚，程桦，等.内层钢板高强钢筋混凝土复合井壁数值模拟[J]. 广西大学学报(自然科学版), 2010,35(1):35-38.

[2]徐志伟，邵鹏，商翔宇，等.深厚表土地压误差对冻结壁厚度设计的影响[J]. 中国矿业大学学报, 2014,43(4):606-611.

[3]LEE S W, JUNG J W, NAM S W, et al. The influence of seepage forces on ground reaction curve of circular opening[J]. Tunnelling and Underground Space Technology, 2006, 22(1) : 28-38.

[4]王衍森，黄家会，李金华，等 冻结井外壁高强混凝土的早期强度增长规律研究[J]. 中国矿业大学学报, 2008,37(5):595-598.

[5]荣传新，程桦.冻结井钢筋混凝土弧形板井壁力学特性研究[J]. 岩石力学.2006, 27(2):193-198.

[6]YAO Z S, YANG J J, SUN W R.Experimental study on sliding shaft lining mechanical mechanisms underground subsidence conditions[J]. Journal of Coal Science and Engineering, 2003, 9 (1):95-99.

[7]姚直书，程桦，杨俊杰.深表土中高强钢筋混凝土井壁力学性能的试验研究[J]. 煤炭学报，2004，29(2)：167-171.

[8]姚直书，薛维培，宋海清，等.富水松软岩层冻结法凿井井壁结构试验研究[J]. 广西大学学报(自然科学版), 2014, 39 (2):231-236.

[9]荣传新, 王秀喜, 程桦，等.深厚冲积层高强钢筋混凝土井壁力学特性研究[J]. 岩石力学与工程学报，2008，27(S1): 2841-2847.

[10]徐秉业，刘信声.应用弹塑性力学[M]. 北京:清华大学，1995.

[11]张远高，陆明万.混凝土的三参数破坏准则[J]. 上海交通大学学报, 1990,24(5,6):62-88.

[12]过镇海，王传志.多轴应力下混凝土的强度破坏和破坏准则研究[J]. 土木工程学报，1991,24(3): 1-13.

[13]YAO Z S, CHANG H, RONG C X.Research on stress and strength of high strength reinforced concrete drilling shaft lining in thick top soils[J]. Journal of China University Mining & Technology,2007,17(3):0432-0435.

[14]李朝弟.结构的安定性与极限分析[D]. 北京: 清华大学, 1991.

[15]KUPFER H, SHINOZUKA M, SCHELLER G, et al.Behavior of concrete under biaxial stress[J]. American Concrete Institute, 1969, 66(8): 656-666.

[16]中华人民共和国国家标准编写组.GB50010-2010 混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2010.

(责任编辑唐汉民裴润梅)

Mechanical properties of high-strength concrete shaft lining based on three-parameter strength criterion

LI Xue-mei, RONG Chuan-xin, CHENG Hua

(School of Civil Engineering and Architecture, Anhui University of Science and Technology, Huainan 232001, China)

Abstract:In order to analyze the mechanical properties of high-strength concrete shaft lining, the three-parameter strength criterion was used to obtain the theoretical ultimate bearing capacity of the high-strength concrete shaft lining and the analytical expressions among stress, radius and the loads in both elastic and plastic regions. The calculated results were verified by experimental results. The results show that the radial stress σr increases while the circumferential stress σ(θ) decreases with the increase of radius r in the elastic region. The radial stress σr and the circumferential stress σ(θ) increase with the increase of radius r in the plastic zone. The ultimate bearing capacity of the shaft lining pp is 22.87 MPa when the thickness of the shaft lining is 1.0 m and the concrete strength is C60. The ultimate bearing capacity of the shaft lining increases by about 2.8 MPa when the thickness increases by 0.1 m. And the circumferential stress of the concrete shaft lining reaches 164.38 MPa, which is about 2.7 times of the uniaxial compressive strength of concrete cubes and demonstrates that the three-parameter strength criterion, considering the influence of multi-axial strength of concrete, is more applicable to analyze the mechanical properties of high-strength concrete shaft lining. It provides a theoretical reference for structure design and calculation of high strength-concrete shaft lining.

Key words:three-parameter strength criterion; high strength concrete shaft lining; ultimate bearing capacity; shaft lining stress

中图分类号:TD262

文献标识码:A

文章编号：1001-7445(2016)02-0308-09

doi:10.13624/j.cnki.issn.1001-7445.2016.0308

通讯作者：荣传新(1968—)，男，安徽六安人，安徽理工大学教授，博士生导师，博士；E-mail: chxrong@aust.edu.cn。

基金项目：国家自然科学基金资助项目(51374010，51474004)

收稿日期：2015-11-01；

修订日期：2016-01-21

引文格式：李雪梅，荣传新，程桦.基于三参数强度准则的高强混凝土井壁力学特性分析[J].广西大学学报(自然科学版)，2016，41(2)：308-316.