渗流理论在多个染病阶段的疾病传播中的应用

霍娅鲜，靳　祯

(1.中北大学理学院，山西太原　030051；2.山西大学复杂系统研究所, 山西太原　030006)



渗流理论在多个染病阶段的疾病传播中的应用

霍娅鲜1，靳祯2

(1.中北大学理学院，山西太原030051；2.山西大学复杂系统研究所, 山西太原030006)

摘要：为了研究具有多染病期的疾病在人群中传播所形成的疾病爆发情况，将疾病传播网络研究和生成函数理论与渗流原理结合起来，使得网络的拓扑结构更加清晰和便捷。把染病期分为n个阶段：I1，I2，…，In，得出了由一个染病节点开始在网络中传播所引起的疾病的爆发阈值、爆发规模、疾病爆发时染病节点的平均度、未染病节点的平均度等的计算方法。

关键词：应用数学；生成函数；渗流原理；染病阶段；爆发阈值；爆发规模

随着科学技术的发展，科研工作者对网络的研究所涉及的不仅有社会网络[1-3]、技术网络[4-5]、合作网络，还有生物网络[6-7]，并且从中获得了一系列细节方面的计算、检查和模拟，许多研究者已经把这些理论应用到了疾病传播方面[8-14]。

许多疾病是通过人与人之间的接触在人群中传播的。当染病者和易感者接触时，疾病会从染病者传向易感者，这种引起疾病传播的接触形式就形成了一个网络。假设网络中每个节点代表1个人，2个人有接触就在这2个节点之间连边。连接在1个节点的边数叫做节点的度。假设网络中任意1个节点度为k的概率为Pk，可以通过设置网络的概率密度函数Pk来得到一个网络。

把每个个体的状态分为易感者S，染病者I,所处的不同染病阶段记为I1，I2，…，In，恢复者R。 易感者S是指没有染病，但易被染病者传染的个体；染病者I指已经染病且具有传染能力的个体；I1，I2，…，In指染病者I所处于染病期的不同阶段，在不同的染病阶段染病者I具有不同的传染能力；恢复者R指染过病，但已经痊愈的个体，这样的个体具有免疫能力不会再被感染。把染病者I所处的阶段分为n个阶段是有意义的，因为在有些疾病中，有的染病阶段染病者具有高传染性，有的染病阶段染病者具有低传染性。所以把染病期假设为n个阶段更精确，也更加符合实际情况。

⋮

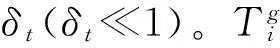
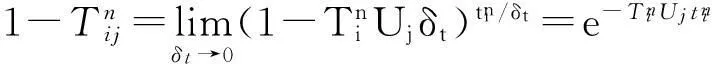
以上的分析是在时间连续的情况下进行的。而在有些情况下，需要指定一段时间长为单位1，这样时间就可以看成是离散的。在时间离散的情况下，不取极限，而是简单地令δt=1[15]， 此时有：

⋮

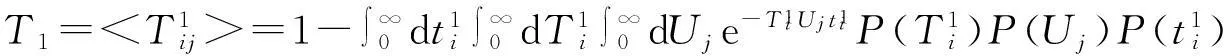
(1)

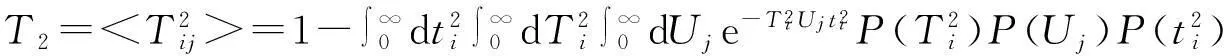
(2)

⋮

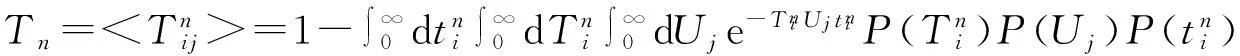
(3)

对于时间离散的情况，有[15]：

(4)

(5)

⋮

(6)

在下面的分析中，直接用每一阶段的平均传染率T1,T2,…,Tn。

1生成函数

依据有边占用概率T1，T2，…，Tn的边渗流原理进行分析，由一个染病节点开始在网络中传播所形成的疾病爆发情况，使得网络研究更加清晰便捷。采用生成函数的方法来解决[16-17]。 参照NEWMAN 等[18]的定义，对关于度分布的生成函数定义如下：

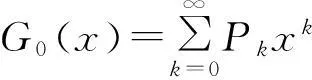
(7)

若Pk被正规化，则当x为1时，有G0(1)为1。在下面的讨论中，都假设Pk被正规化。

这个函数包含了关于度分布的所有信息。给了这个生成函数，就能够计算出任意一个节点度为k的概率[18]：

(8)

生成函数具有以下性质：

1)幂： 如果已知网络中所有节点度分布的生成函数G0(x)，那么如果任选m个节点，关于这m个节点度的和的分布可由[G0(x)]m得到[18]。

比如，要计算网络中任选2个节点度的和为3的概率，则可以先计算[G0(x)]2。

[G0(x)]2= [∑kPkxk]2=∑j,kPjPkxj+k=

P0P0x0+(P0P1+P1P0)x1+

(P0P2+P1P1+P2P0)x2+(P0P3+P1P2+P2P1+P3P0)x3+…。

那么网络中任选2个节点度的和为3的概率为式中x3的系数。对于生成函数的更高次幂也符合上面的性质[18]。

2)矩： 由一个生成函数生成的网络中节点度的平均值是由这个生成函数的一阶导数在自变量为1时计算出的[18]。例如，一个节点的平均度是：

(9)

分布的高阶矩也能够通过高阶导数计算出来[18]，即：

设G1(x)是随机选择一条边到达的节点的余度分布的生成函数。余度指除选的那条边以外的边的数目，即度减去1。根据NEWMAN等[18]的描述，有以下结论：

(10)

且

(11)

这里z是节点的平均度。

利用渗流原理来研究网络中由一个染病节点开始引起的疾病传播，把疾病(病原体)通过的边做标记或者说它被“占用”。那么疾病的最终爆发规模正是那些通过占用边到达的节点的巨连通片的大小[15]。

为了建立网络中的疾病传播和物理中渗流理论之间的关系，当边中有病原体在传播时，可对边做标记或者说它被“占用”[15]。 那么对于一个度为k的节点，它有m条边被占用的概率如下：

因此m的概率分布的生成函数(即m的概率母函数)是[15，19]:

G0(x;T1,T2,…,Tn)= ∑∞k=0Pk∑km=0kmæèçöø÷∑mm1=0mm1æèçöø÷Tm11∑m-m1m2=0m-m1 m2æèçöø÷Tm22æèç…

(1-T1-T2-…-Tn)k-mxm=

G0(1+(x-1)T1+(x-1)T2+…+(x-1)Tn),

(12)

同理，随机选择一条边，通过跟随这条边到达的节点的其余的边中有m条边被占用的概率是：

G1(x;T1,T2,…,Tn)=G1(1+(x-1)T1+(x-1)T2+…+(x-1)Tn),

(13)

根据定义，有：

G0(x;1,1,…,1)=G0(nx-n+1),

G0(1;T1,T2,…,Tn)=G0(1),

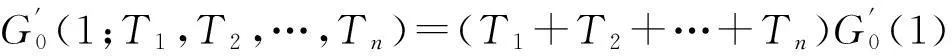
对于G1(x;T1,T2,…,Tn)，同样有:

G1(x;1,1,…,1)=G1(nx-n+1),

G1(1;T1,T2,…,Tn)=G1(1),

图1　连通片包含情况示意图Fig.1　Internal components of the connected component

图1中的正方形表示一个连通片，圆圈表示1个节点。这个图表示跟随随机选择的1条边到达的终端是1个连通片，包括以下情况：这个连通片包括1个节点；这个连通片包括1个节点以及由这个节点引出的1个小连通片；这个连通片包括1个节点以及由这个节点引出的2个小连通片；……；这个连通片包括1个节点以及由这个节点引出的n个小连通片。

2疾病的爆发规模

疾病的爆发规模，即在网络中通过占用边连接在一起的节点的连通片的规模。为了得到这一重要数据，定义一个关于爆发规模的生成函数(即爆发的节点数量为s的概率母函数)：

(14)

为了得到s的平均值，先来定义H1(x;T1,T2,…,Tn)是通过随机选择1条边到达的1个连通片的大小的生成函数。在这里假设图中没有环，完全是树状的。由图1可以看出该连通片包含以下情况：只有1个节点；有1个节点，并且节点连接着1个连通片；有1个节点，并且节点连接着2个连通片；……；有1个节点，并且节点连着n个连通片。

H1(x;T1,T2,…,Tn)=xq0+xq1H1(x;T1,T2,…,Tn)+xq2[H1(x;T1,T2,…,Tn)]2+

…+xqk[H1(x;T1,T2,…,Tn)]k+…,

即：

H1(x;T1,T2,…,Tn)=xG1(H1(x;T1,T2,…,Tn);T1,T2,…,Tn)。

(15)

图2　　　随机选择1个点所在的连通片　　　包含情况示意图Fig.2　　　Internal components of the component to 　　　which a randomly chosen verticle belongs

如果从随机选择的1个节点开始，从这个节点出发的每1条边都有1个这样的连通片，如图2所示，那么包含这个节点在内的整个连通片的大小的生成函数为

H0(x;T1,T2,…,Tn)=

xP0+xP1H1(x;T1,T2,…,Tn)+

xP2[H1(x;T1,T2,…,Tn)]2+

…+

xPk[H1(x;T1,T2,…,Tn)]k+

…，

即：

H0(x;T1,T2,…,Tn)=

xG0(H1(x;T1,T2,…,Tn);T1,T2,…,Tn)。

(16)

与式(8)类似，当有了H0(x;T1,T2,…,Tn)，就能用式(14)得到Ps(T1,T2,…,Tn)。但是在大多数情况下，找到H0的任意阶导数是不可能的。所以用柯西积分来找它的近似算法:

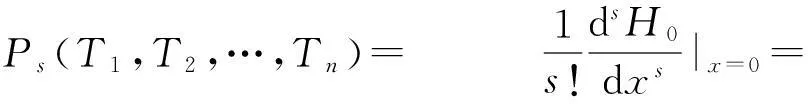
Ps(T1,T2,…,Tn)= 1s!dsH0dxs|x=0=

(17)

这样把求导转化为了求周线上的积分。根据文献[20]甚至可以找到一个方程的第一千阶导数。所以根据渗流理论，假设的模型中疾病将感染s个人的概率为Ps(T1，T2，…，Tn)。

3爆发规模、爆发阈值以及被感染个体的均度

假设Ps(T1，T2，…，Tn)为爆发规模的完整分布，现在求平均爆发规模。

由式(9)和式(16)得：

把式(15)进行微分，有：

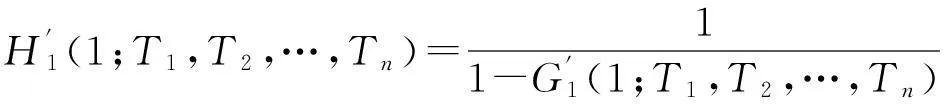
因此:

(18)

这样，就得出了对于任何的T1，T2，…，Tn值，染病者的平均数目，即疾病的平均爆发规模。

(19)

当T1+T2+…+Tn≥Tc时，有一个染病者巨连通片，即“巨片”在渗流中。此时网络不再是树状结构，所以式(15)和式(16)不再有效。

现在再来讨论网络中存在“巨片”的情况。需要对H0重新定义为除“巨片”以外的其他小连通片大小的生成函数，即不连接到染病者巨连通片的孤立的小连通片。因此在T1+T2+…+Tn≥Tc时，有：

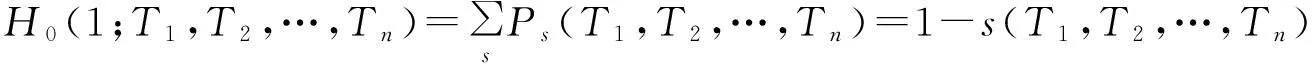
(20)

在这里s(T1，T2，…，Tn)是染病者巨连通片在整个图中所占的比例。

由式(16)和式(20)，得：

s(T1,T2,…,Tn)=1-H0(1;T1,T2,…,Tn)=1-G0(u;T1,T2,…,Tn)，

(21)

这里u≡H1(1;T1,T2,…,Tn)，由式(15)得，它是下列自相容方程的解：

u=G1(u;T1,T2,…,Tn)。

(22)

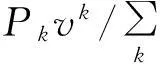
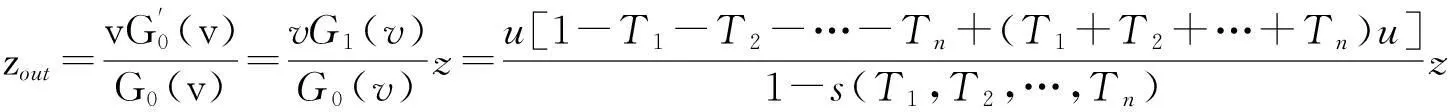
(23)

相似的，在所有染病的节点中选择一个节点度为k的概率是由生成函数[G0(x)-G0(vx)]/[1-G0(v)]生成的[15]，下式给出了“巨片”中一个节点的平均度zin：

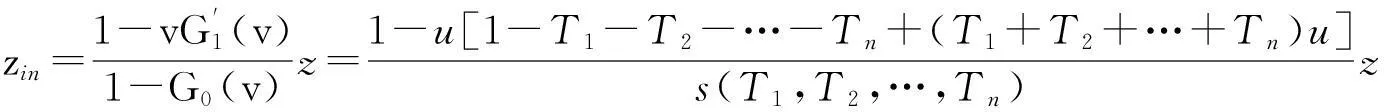
(24)

可以证明：

u[1-T1-T2-…-Tn+(T1+T2+…+Tn)u]/[1-s(T1,T2,…,Tn)]≤1,

[1-u[1-T1-T2-…-Tn+(T1+T2+…+Tn)u]]/s(T1,T2,…,Tn)≥1,

所以zout≤z,zin≥z。 即染病节点的平均度大于等于所有节点的平均度，未染病节点的平均度小于等于所有节点的平均度。

由此可以得出，度小的节点不易染病，因此在有传染病威胁时可以通过减少自己与他人的接触来预防疾病，如减少走亲访友与外出旅游的次数，戴口罩以减少直接接触的次数等。

4结语

本文应用渗流原理和生成函数理论研究了网络中的疾病传播。其特别之处在于，把染病期分为n个阶段，染病者在每一阶段的传染率都不同，计算出了疾病的爆发阈值、爆发规模、染病节点的平均度等。本文的研究方法可以应用于疾病传播以及信息传播方面的研究。在信息传播研究方面，可以假设以天为单位，每一个得知信息的人在得知信息以后，随着时间的推移，把信息传播出去的概率是不同的，采用本文介绍的方法，可以得到最后这个信息有多少人获得等数据，从而预判信息在人群中所造成的影响力。

参考文献/References:

[1]WATTSDJ,STROGATZSH.Collectivedynamicsof‘smallworld’networks[J].Nature, 1998, 393(6684): 440-442.

[2]LILJEROS F, EDLING C R, AMARAL L A N, et al. The web of human sexual contacts[J].Nature, 2001, 411(6840):907-908.

[3]汪小帆, 李翔, 陈关荣. 网络科学导论[M].北京：高等教育出版社, 2012.

[4]ABELLO J, BUCHSBAUM A L, WESTBROOK J R. A functional approach to external graph algorithms[C]//Algorithms-ESA’98 Berlin: Springer, 1998: 332-343.

[5]FALOUTSOS M, FALOUTSOS P, FALOUTSOS C. On power-law relationships of the internet topology[C]//Proceedings of the Conference on Application,Technologies,Architectures and Protocols for Computer Communication.SIGCOMM'99.[S.l.]:[s.n.],1999:251-262..

[6]JEONG H, MASON S P, BARABSSI A L, et al. Lethality and centrality in protein networks[J]. Nature, 2001, 411(6833):41-42.

[7]WILLIAMS R J, MARTINEZ N D. Simple rules yield complex food webs[J]. Nature, 2000, 404(6774): 180-183.

[8]MOORE C, NEWMAN M E J. Epidemics and percolation in small-world networks[J]. Physical Review E, 2000,61(5): 5678.

[9]PASTOR-SATORRAS R, VESPIGNANI A. Epidemic spreading in scale-free networks[J]. Physical Review Letters, 2001,86(14): 3200.

[10]MORENO Y, PASTOR-SATORRAS R, VESPIGNANI A. Epidemic outbreaks in complex heterogeneous networks[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2002, 26(4): 521-529.

[11]WARREN C P, SANDER L M, SOKOLOV I M. Firewalls, disorder, and percolation in epidemics[EB/OL].http://arXiv preprint cond-mat/0106450, 2001-06-21.

[12]KARRER B, NEWMAN M E J,ZDEBOROVA L. Percolation on sparse networks[J]. Physical Review Letters, 2014, 113(20): 208702.

[13]宋瑞, 靳祯. 复杂网络上不同染病期疾病的传播及控制研究[J]. 中北大学学报(自然科学版), 2014, 35(2): 93-96.

SONG Rui,JIN Zhen.The spread and control of epidemic with different infectious period in complex networks[J].Journal of North University of China(Natural Science Edition),2014, 35(2): 93-96.

[14]宋瑞, 靳祯. 复杂网络上阶段性传染病动力学分析[J]. 复杂系统与复杂性科学, 2014, 11(3): 73-78.

SONG Rui,JIN Zhen.Dynamics analysis of staged progression epidemic model on complex networks[J].Complex Systems and Complexity Science,2014, 11(3): 73-78.

[15]NEWMAN M E J. Spread of epidemic disease on networks[J]. Physical Review E, 2002, 66(1): 016128.

[16]WILF H S. Generating Functionology[M]. New York: Academic Press Inc,2013.

[17]WANG J, ZHOU Z, ZHANG W, et al. Bond and site percolation in three dimensions[J]. Physical Review E, 2013, 87(5): 052107.

[18]NEWMAN M E J, STROGATZ S H, WATTS D J. Random graphs with arbitrary degree distributions and their applications[J]. Physical Review E, 2001, 64(2): 026118.

[19]MEYERS L A, NEWMAN M E J, POURBOHLOUL B. Predicting epidemics on directed contact networks[J]. Journal of Theoretical Biology, 2006, 240(3): 400-418.

[20]MOORE C, NEWMAN M E J . Exact solution of site and bond percolation on small-world networks[J]. Physical Review E, 2000, 62(5): 7059.

Application of percolation theory in pathophoresis during multiple stages of the infected period

HUO Yaxian1， JIN Zhen2

(1.School of Science, North University of China, Taiyuan，Shanxi 030051, China；2.Complex Systems Research Center, Shanxi University, Taiyuan， Shanxi 030006, China)

Abstract:Network study combined with the generating function and percolation theory is used to study the outbreak of infectious disease with multiple infected stages among people, so the network topology is made more clear and convenient. The infected period is divided into n stages: I1, I2,…,In. The calculation of the disease outbreak threshold, the scale of outbreaks,the mean degree of infected nodes, and the mean degree of uninfected nodes in the spreading epidemic caused by one infected individual are obtained.

Keywords:applied mathematics; generation function; percolation theory; stages of infected period; the outbreak threshold; the scale of the outbreak

中图分类号：O173；N949MSC(2010)主题分类：34N05

文献标志码：A

通讯作者：靳祯教授。E-mail：jinzhn@263.net

作者简介：霍娅鲜(1991—)，女，山西晋城人，硕士研究生，主要从事生物数学方面的研究。

基金项目：山西省科技创新团队项目(2015013001-06)；山西省高校优秀创新团队项目(232548901001)；山西省回国留学人员重点科研资助项目(2013-重点)

收稿日期：2015-10-09；修回日期：2015-12-12；责任编辑：张军

doi:10.7535/hbkd.2016yx02008

文章编号：1008-1542(2016)02-0160-07

霍娅鲜，靳祯.渗流理论在多个染病阶段的疾病传播中的应用[J].河北科技大学学报,2016,37(2):160-166.

HUO Yaxian，JIN Zhen.Application of percolation theory in pathophoresis during multiple stages of the infected period[J].Journal of Hebei University of Science and Technology,2016,37(2):160-166.