某汽车发动机护板的有限元分析及优化设计

刘　学，王奕睿，李志磊，张兴宇，乔冠翔

（武汉理工大学　现代汽车零部件技术湖北省重点实验室，湖北　武汉　430070）

Liu Xue，Wang Yirui，Li Zhilei，Zhang Xingyu，Qiao Guanxiang



某汽车发动机护板的有限元分析及优化设计

刘学，王奕睿，李志磊，张兴宇，乔冠翔

（武汉理工大学现代汽车零部件技术湖北省重点实验室，湖北武汉430070）

Liu Xue，Wang Yirui，Li Zhilei，Zhang Xingyu，Qiao Guanxiang

摘要：以某型汽车发动机护板为分析对象，采用CATIA软件建立汽车护板模型；以有限元分析软件HyperWorks为平台，对护板进行模态分析，并应用OptiStruct软件对护板进行形貌优化，选择1阶频率最大化作为目标函数，并满足护板刚度和强度的约束条件。根据优化的分析结果，将其与加工工艺结合在一起，布置下护板加强筋，并对优化方案进行模型验证，结果显示发动机护板的1阶频率提高了29.96％，优化效果良好，避开了发动机的激振频率，为发动机护板设计加强筋提供了新的方法。

关键词：发动机护板；HyperWorks；有限元分析；形貌优化

0　引　言

在汽车发展过程中，发动机下护板在汽车安全行驶过程中起着至关重要的作用。发动机下护板是根据各自车型设计的发动机防护装置，主要由护板、通风孔、螺栓孔和加强筋等结构组成，设计的目的主要是防止泥沙飞溅到发动机，其次是在行驶过程中防止高低不平的路面对发动机造成撞击，造成发动机的损坏。通过发动机下护板的保护延长发动机的使用寿命，减小事故发生的概率，避免行驶过程中路面刮碰发动机导致汽车抛锚。国内外许多工程师和学者也发现了发动机下护板的优越性能，对下护板进行了探索研究，但大多集中在对下护板的理论研究[1]，文中的重点是解决下护板的结构优化问题。

下护板安装在发动机的下方，在工作过程中下护板和发动机有可能会产生共振，因此下护板的模态是安全使用的保证。发动机工作频率一般是15～60Hz，所以发动机下护板1阶频率应尽可能地避开发动机工作频率，避免下护板和发动机产生共振，影响下护板的使用。

对下护板的频率进行分析，结果显示：下护板的1阶模态比较接近发动机工作频率。为了解决发动机下护板的模态问题，在保证下护板刚度和强度的同时，提高下护板的1阶频率，使其大于发动机的一般工作频率即大于60Hz，保证其远离发动机工作频率。将此问题定义为约束条件下的局部优化问题，对发动机下护板进行模态分析及形貌优化，提出优化设计方案以提高1阶频率，计算出合理的结构，为汽车零部件关键技术方面的研制与开发提供重要的参考依据。

1　有限元模型建立

1.1下护板实体模型

根据某型汽车发动机的需要，利用CATIA软件[2]设计一款发动机下护板，以满足发动机防护的需要，发动机下护板CATIA模型如图1所示，下护板主要由板件本体、通风孔和加强筋结构组成，其中板件本体厚度为1.5mm，局部区域为1.2mm，发动机下护板总质量为2.8kg左右，满足技术规范要求，下护板通过4个安装孔和1个预挂点安装固定。

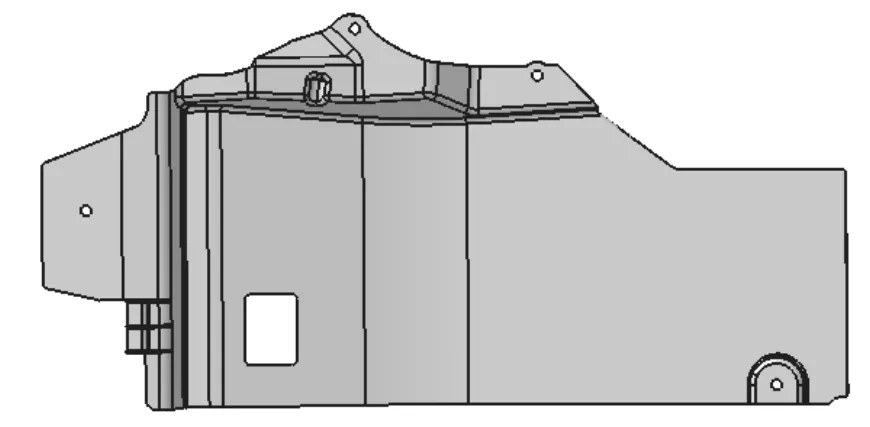
图1　下护板实体模型

1.2下护板有限元模型

几何模型的质量高低直接影响分析的结果，对原模型进行有限元分析时，需要对其进行简化。下护板几何模型是对分析对象尺寸和形状的描绘，是从实际形状中抽象出来的，在建立有限元模型时，应该根据研究对象的具体特征，对下护板结构进行必要的简化处理，以适应有限元的特点[3]。下护板的主要厚度为1.5mm，其长度方向的尺寸远远大于厚度方向尺寸，符合壳单元的理论假设，因此对壳单元进行离散，采用5mm大小的网格进行有限元网格划分，以获得比较高的计算精度。发动机下护板有限元模型如图2所示，以四边形单元为主，少量三角形过渡，有限元模型共计9369个单元，9489个节点，其中三角形单元占0.13％，网格质量较高，下护板本体与加强筋之间通过节点耦合模拟。

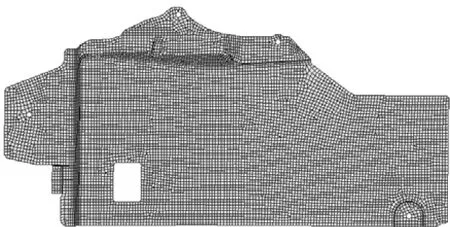
图2　下护板有限元模型

2　模态分析

在评价下护板结构动态设计时，固有频率和振型是结构的重要参数，因此可以得出模态分析是动态分析核心。模态分析是机械零部件或结构的动态特性分析的一种重要形式，其结果是为了得到结构的固有频率和振型[5-6]。

基于线性振动原理和有限元法，对于一个多自由度线性系统，其运动微分方程

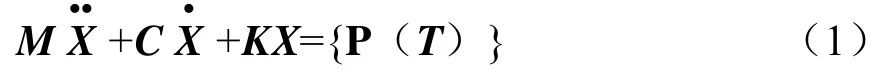
傅里叶变换方程为

由式（4）可得，频率与刚度成正比，与质量成反比，因此提高下护板的频率有2种方法，一是提高下护板的刚度，二是减小下护板的质量。

对于发动机下护板选材，材料的弹性模量为2.09×105MPa，泊松比为0.269，密度为7.89×103kg/m3，抗拉强度600MPa，屈服强度355MPa。

下护板用螺钉安装在发动机下方，不能自由运动，所以对下护板进行约束模态分析。在下护板4个安装孔位置约束X、Y、Z向的平动和转动自由度，在预挂点位置约束Z向平动自由度。采用线性分析软件Radioss计算其模态，有限元分析发动机下护板前8阶约束模态频率如表1所示，前2阶频率显示如图3、图4所示。

表1　下护板前8阶频率Hz

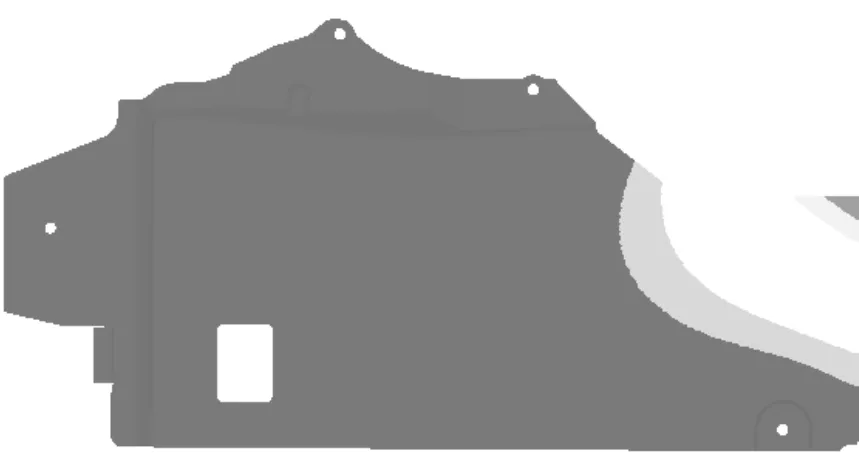
图3　1阶模态振型云图

图4　2阶模态振型云图

由分析可知发动机下护板1阶模态频率为51.36Hz，小于技术规范要求的60Hz，下护板容易与发动机共振，导致下护板应力集中，损坏下护板，因此不满足技术要求。

3　结构优化

3.1形貌优化

基于发动机下护板的1阶频率和模态云图，为了加强下护板的刚度和强度，提高1阶频率，采用提高下护板刚度的方法，即在下护板平面上布置加强筋[7]，加强筋对下护板的模态以及刚度、强度有较大的影响。为了提高下护板的1阶频率[8]，对下护板采用形貌优化，从而确定加强筋的形状和位置。在形貌优化中，设计空间由大量的节点波动向量组成，这些节点波动向量按照一定的模式进行组合以满足设计约束，生成了优化后的最佳形貌。通过最大化下护板的动态响应，使下护板的最低频率高于发动机的激振频率，从而避免了下护板与发动机的共振。形貌优化数学模型为

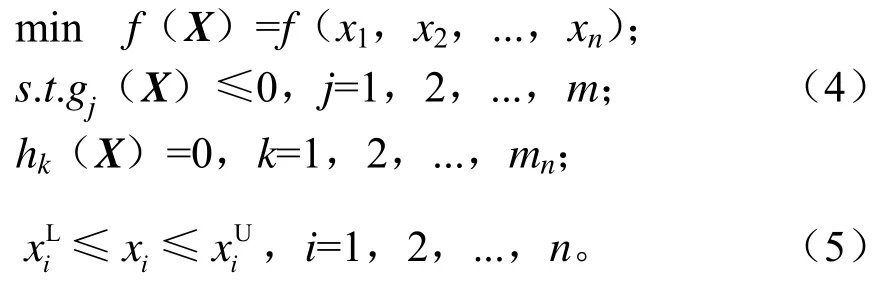
式中，X为设计变量；f（X）为目标函数；g（X）为不等式约束函数；h（X）为等式约束函数；为设计的下限；为设计的上限。

3.2优化参数设定

用有限元软件OptiStruct进行形貌优化，确定一个布置加强筋区间。由于下护板网格节点变形后起筋与未起筋区域之间网格变化较大，容易导致网格变形，因此浅色区域（图5）不能做设计区域；安装孔区域没有合适的起筋平面也不能作为设计区间，确定设计区间为深色区域，如图5所示。下护板的迎风面最好平整，最终设计区间选定背风平面区域。

形貌优化在下护板平端面结构上通过对目标函数、约束条件和设计变量的设定，进行迭代运算得到最佳加强筋布置位置。其中，根据单元尺寸的大小，加强筋的设计宽度为6mm，起筋角为60°；根据冲压工艺以及材料的形成特点，起筋最大高度为4mm，节点位移变量为xi，下限为0mm，上限为4mm，其约束条件为控制下护板节点位移变量0≤xi≤4mm，i=1，2，3，…，n。考虑到下护板的1阶频率较小，因此将下护板的1阶频率最大化作为目标函数，提高1阶频率，使其达到设计要求，如图6所示。

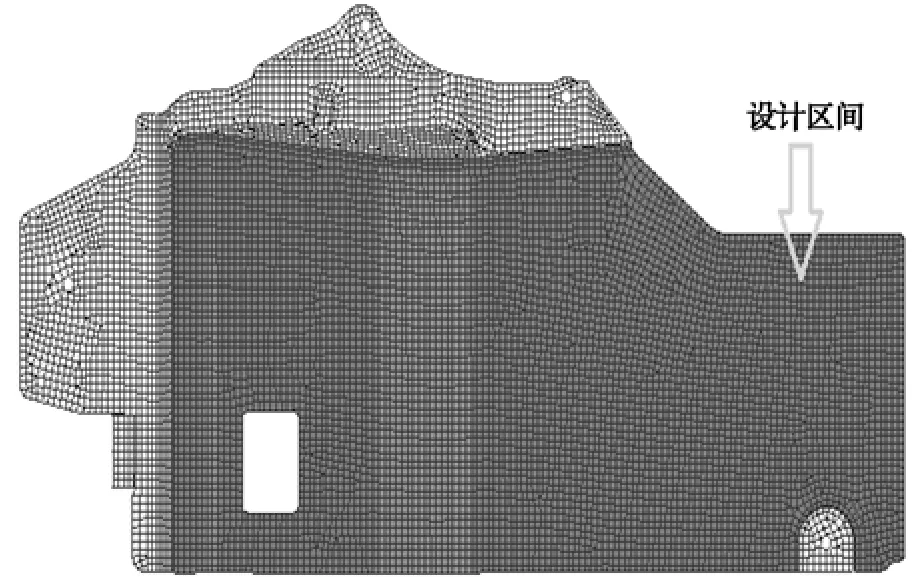
图5　设计区间

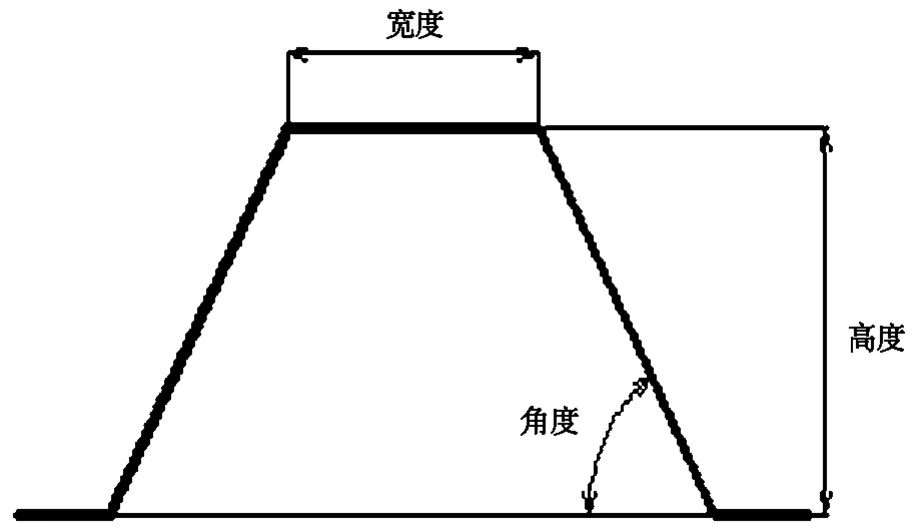
图6　加强筋参数

3.3优化结果处理

经过12轮的迭代计算，得到优化后的下护板1阶频率为89.49Hz，1阶频率提高了74.3％，满足设计要求，见表2。

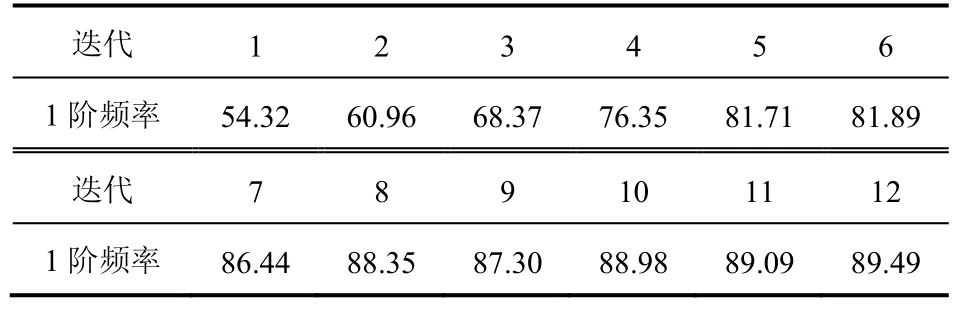
表2　下护板优化迭代过程Hz

优化的过程曲线如图7所示。

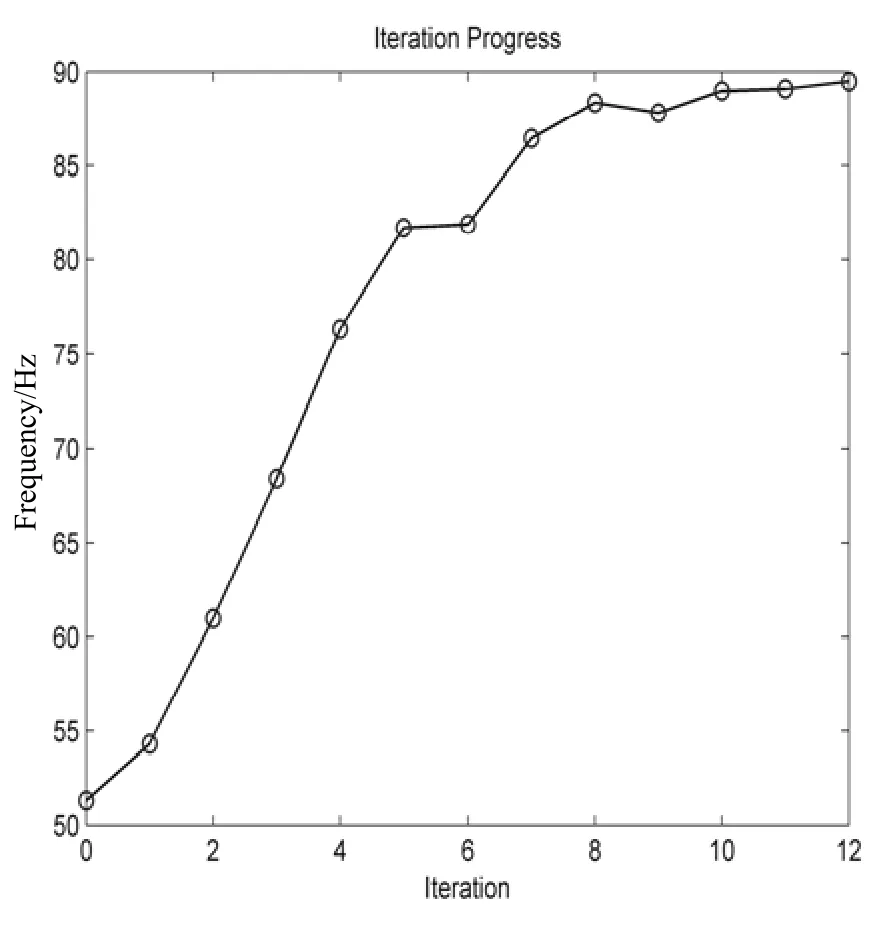
图7　迭代过程

在HyperView中查看下护板形貌优化的云图，标注了加强筋产生处，如图8所示。下护板平端面生成的云图为加强筋的形状及位置提供了依据，利用HyperWorks软件后处理中的OSSmooth工具，可以获得形貌优化的几何图形。由于制造下护板工序增加，提高了制造成本，所以将局部区间的加强筋忽略。考虑到加强筋的易加工性和连续性，以及路面积水进入下护板时的滤水性，根据优化结构建立下护板模型，如图9所示。

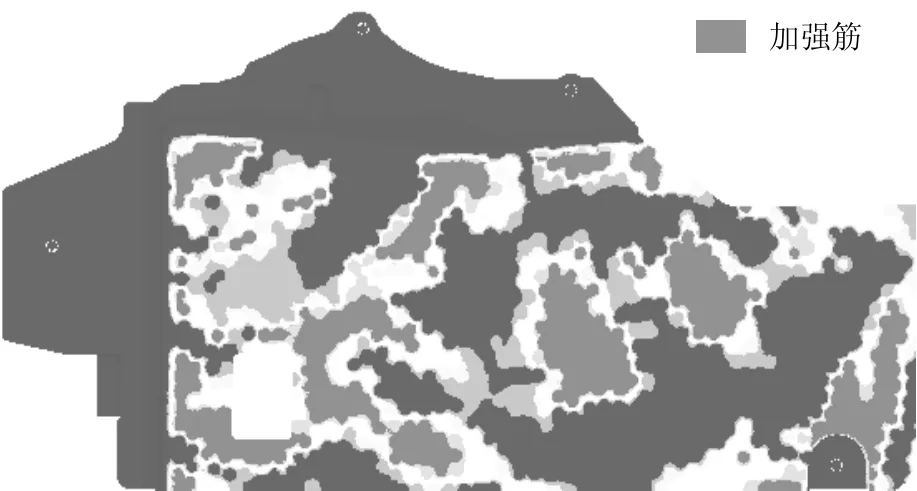
图8　形貌优化结果

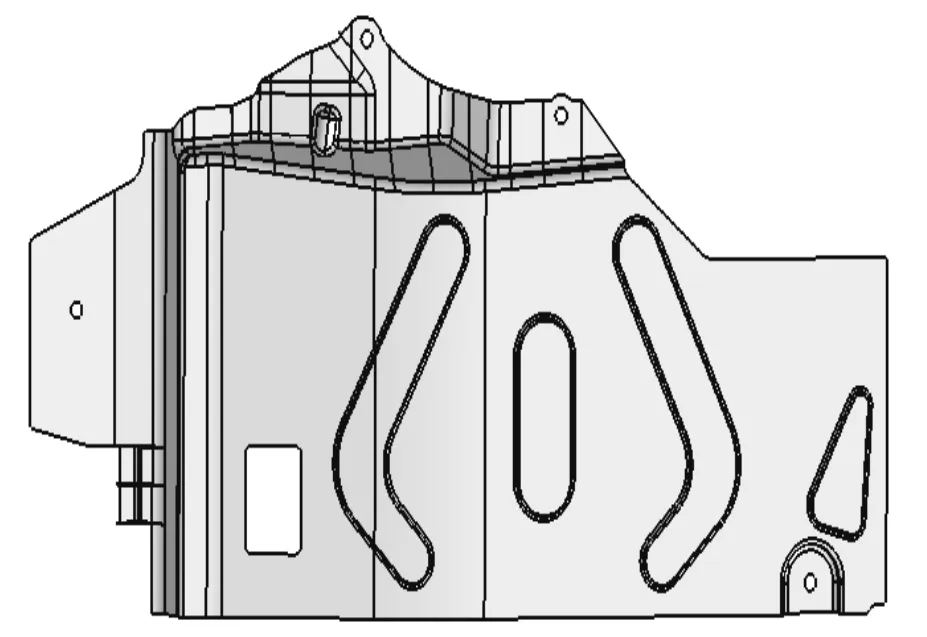
图9　实际下护板加强筋

4　模型验证

为了检验新方案的可行性，对形貌优化后的发动机下护板模型进行模态分析，经计算得到优化后模型的1阶模态和模态云图，在很大程度上提高了下护板结构的1阶频率。1阶模态为89.49Hz，比原始模型模态提高了38.13Hz。经过比较发现，实际模型的1阶模态比12轮迭代优化模型的1阶频率低，是因为在形貌优化中考虑到发动机下护板的加工工艺，忽略掉了一些不必要的加强筋，见表3。

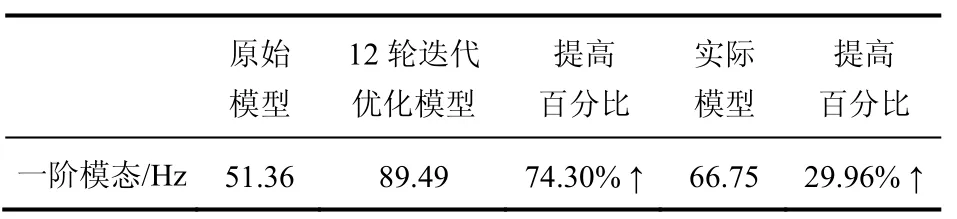
表3　优化模型与原始模型的比较

5　结　论

形貌优化是一种较为理想的优化方法，在板型结构件中寻找加强筋的设计方法来提高结构的模态以及刚度和强度，在优化过程中合理选取参数，获得较满意的形状布局。为了提高发动机下护板1阶约束模态频率，对下护板进行了形貌优化。与原始方案对比，优化后的下护板1阶约束模态频率从51.36Hz提高到66.75Hz，避开了发动机的激振频率（15～60Hz），满足了设计需求，证明了形貌优化的有效性和可行性，为企业发动机下护板设计加强筋提供了新的方法。

参考文献

[1]王萍萍，夏汤忠.CAE技术在某发动机下护板国产化中的应用[C]//中国汽车工程学会.2010中国汽车工程学会年会论文集.2010.

[2]詹熙达.CATIAV5R20快速入门教程[M].北京：机械工业出版社，2011：91-148.

[3]洪清泉，赵康.OptiStruct&HyperStudy理论基础与工程应用[M].北京：机械工业出版社，2012：24-55.

[4]孟祥伟，陈富强.有限元分析在汽车零部件优化设计中的应用[J].客车技术与研究，2012，40（2）：40-42.

[5]马迅，盛勇生.车架刚度及模态的有限元分析及优化[J].客车技术与研究，2004，26（8）：8-11.

[6]邓亚东，邓丽梅.轻型货车驾驶室有限元模态分析与优化设计[J].武汉理工大学学报（信息与管理工程版），2008，30（3）：412-414.

[7]陈塑寰，麻凯.板壳加筋结构的组合优化[J].吉林大学学报（工学版），2008，38（2）：388-392.

[8]Son J H，Kwak B M.Optimization of Boundary Conditions for Maximum Fundamental Frequency of Vibrating Structures[J].AIAA Journal.1993，31（12）：2351-2357.

[9]Murali M.R.Krishna.Topology & Topography Optimization of a Drive Shaft[R].：SAE Technical Paper，2005.

[10]廖芳，王承．支架形貌优化设计方法研究[J].装备制造技术，2009（9）：38-40.

收稿日期：2016-01-08

中图分类号：U464.13

文献标志码：A

DOI：10.14175/j.issn.1002-4581.2016.02.006

文章编号：1002-4581（2016）02-0021-05