罐式危化品多式联运调度模型研究

何红弟， 谢　静， 丁　一， 林国龙

(上海海事大学 物流研究中心，上海 201306)



罐式危化品多式联运调度模型研究

何红弟， 谢静， 丁一， 林国龙

(上海海事大学 物流研究中心，上海 201306)

摘要：随着我国危化品需求的快速增长，危化品运输事故也越频繁。为了降低危化品运输风险，保障运输安全，本文尝试将以罐式集装箱为载体的危化品调度问题与多式联运结合起来，建立了带时间约束的成本和风险最小的多目标规划模型。在此基础上，利用二维欧氏距离客观赋值的模糊算法求解模型。结合算例验证，将多式联运应用到危化品调度问题有利于降低风险，确保调度的安全性。同时，该方法能在风险可控的范围内，实现调度成本的最小化。

关键词：危化品； 罐式集装箱； 多式联运； 调度模型； 模糊算法

化工产业的发展, 促进了化工原料需求的增长。2012年统计显示，我国每年道路危化品在2亿t左右，3000多个品种，铁路危化品货运量占到铁路货运总量的10%。2013年液化品内贸水运总量约2100万t，较上年增长约5%。但是我国危化品生产主要集中在东部沿海，中西部及东北地区偏少，并且需求分散，铁路运力不足，导致危化品过度依赖于公路运输，这对道路安全造成了严重威胁。而多式联运可以克服单一运输方式的不足，在保证充足运力的同时，控制风险与成本。同时，罐式集装箱具有“宜海宜路”、“宜储宜运”、“一罐到底”的优点，可以衔接多种运输方式，确保中转的安全，但是罐式集装箱成本高租金贵，给物流企业带来了巨额的费用。因此，研究从多个起讫点通过多式联运调度罐式危化品有助于物流企业在保证调度安全的同时降低调度成本。

国内外对危化品运输路径优化和多式联运最短路径问题早有研究，但是将危化品调度和多式联运结合起来研究的很少。储庆中[1]建立了风险最小为上层目标，成本最小为下层目标的双层规划模型对危险品运输网络进行优化。种鹏云[2]将风险偏好分为远期风险厌恶型、近期风险厌恶型和风险中性，依此建立了多目标决策模型。宋伟程[3]综合考虑危险品性质、事故类型和环境因素，建立点危险源的路径风险评价模型。杨信丰等[4]选取时间、运输事故的概率、交通损失、暴露人数及应急响应能力描述路段的属性，构建了城市危险品运输路径选择模型。刘慧怡[5]将风险、运距及费用目标抽象成类似广义费用的综合表达形式，并采用Dijkstra算法求解。ASLAN H等[6]基于博弈论的理论基础提出了危险品运输中的风险规避方法。ROJEE PRADHANANGA等[7]提出基于蚁群算法的危险品路径优化，结果表明蚁群算法能够很好地解决带时间窗的路径优化问题。MOHDRAPIKSAAT等[8]研究了北美地区危险品运输的特性，特别针对油罐车设计了基于运输效率和安全的运输模型。姜军等[9]以各运输方式运输费用和运输时间的线性加权之和最小为目标建立模型，并采用改进的遗传算法求解模型。唐建桥等[10]建立了集装箱多式联运组织优化模型，并用模拟退火遗传算法求解模型。刘舰和俞建宁[11]研究了多式联运运输方式选择问题，建立了成本、风险最小的优化模型，并采用克隆增扩的人工免疫算法求解模型。张鹏鸽等[12]分析了西江水系公铁水多式联运现状，根据其时间窗特性建立了基于时间约束的最小费用流数学模型。杨雪[13]提出换装时间函数，建立以总成本最小和总时间最短的多目标0-1整数规划模型，并将时间转化为广义成本对模型进行求解。BAUER[14]建立了一个多式联运碳排量最小模型，并将其应用于东欧铁路网案例的研究。

本文从危化品物流企业的角度出发，尝试将危化品调度与多式联运结合起来，建立了成本和风险最小的多目标模型，研究将罐式危化品从多个供应点通过联运网络调运至多个需求点的问题。通过不同运输方式的组合调度优化，使整个联运网络风险和成本相互平衡，进而避免由于危化品运量增加、供求信息繁杂造成的危险事故频发以及成本剧增现象。

1问题描述和模型建立

1.1 问题描述

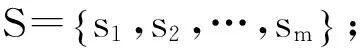
1)供应点供应箱量、需求点需求箱量以及相邻节点间存在的运输方式都已知；

2)供应箱量大于需求箱量；

3)只考虑一种箱型，即20英尺。

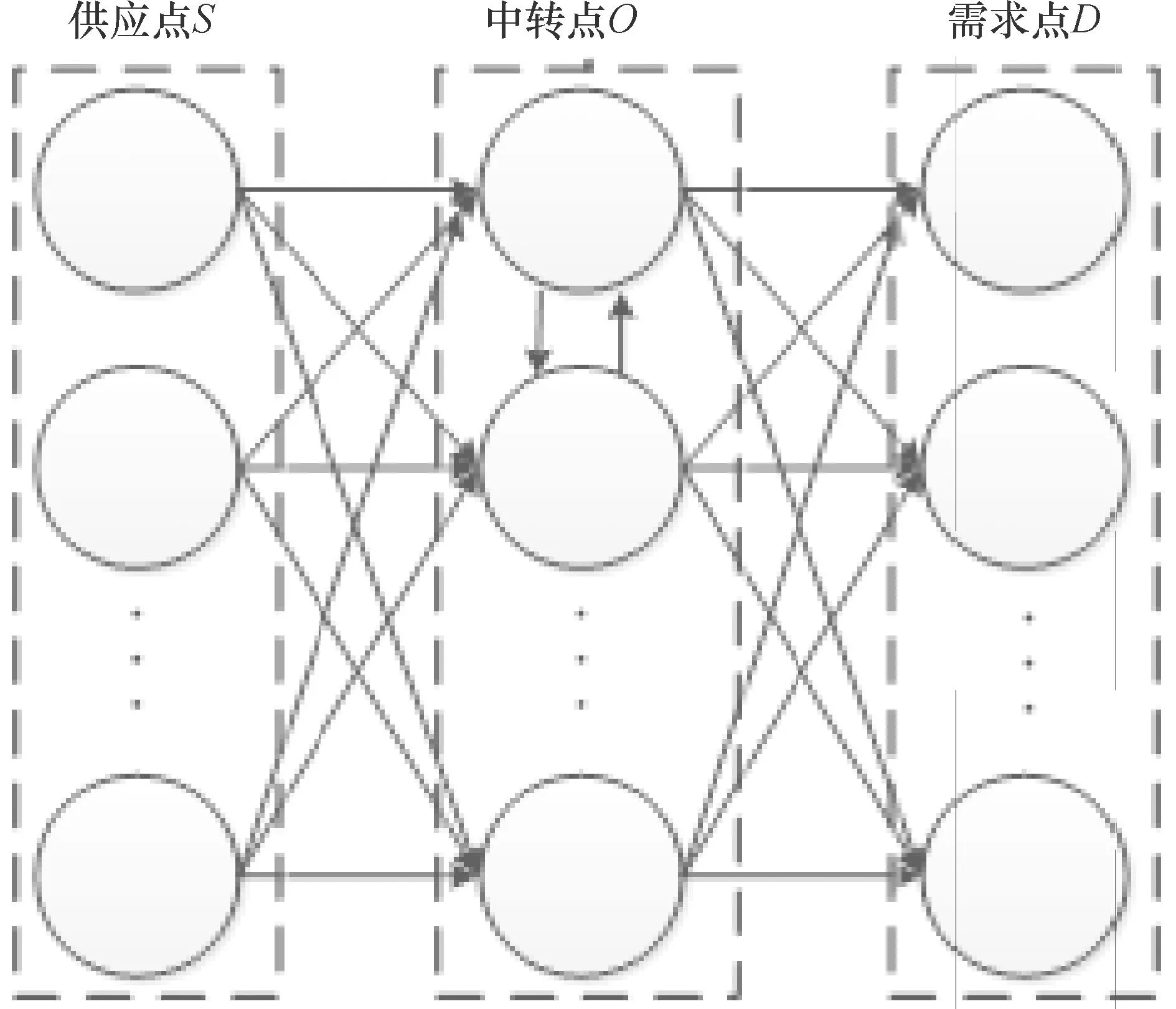
图1　多式联运网络图

1.2模型符号说明

1.3目标函数与约束条件

调度成本与调度风险一直是物流企业不可调和的矛盾所在，据此文章建立了成本与风险最小的两个目标函数：

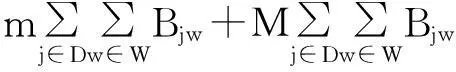
(1)

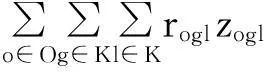
(2)

式(1)总成本由运输成本、中转成本、罐式集装箱租箱成本和管理成本组成；式(2)总风险由运输风险和中转风险组成。

约束条件为：

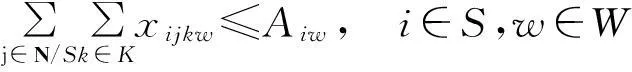
(3)

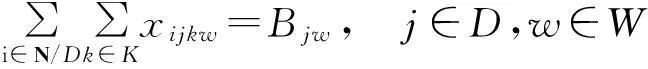
(4)

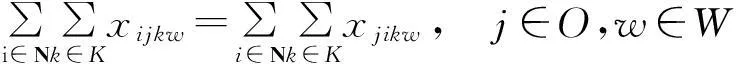
(5)

xijkw≤Qijkwyijkw≤πxijkw

(6)

yiogwyojlw=zogl,i,j∈N，g,l∈K，w∈W；

(7)

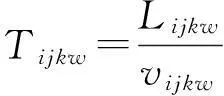
(8)

Tif=0,i∈S；

(9)

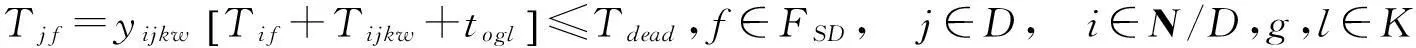
(10)

xijkw≤Qijkw,i,j∈N；

(11)

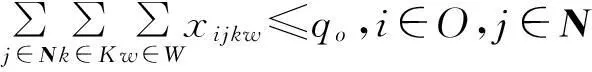
(12)

yijkwRijkw≤Hmax；

(13)

zoglrogl≤hmax,g,l∈K，o∈O。

(14)

式(3)表示供应点S提供危化品w的箱量要不小于实际输出供应点S的危化品w箱量；(4)表示需求点D危化品w的需求箱量等于实际输入到节点D的危化品w箱量；(5)表示中转点流量守恒，运入到中转点O危化品箱量等于运出箱量；(6)表示是否存在箱量分配；(7)确保转运的连续性；(8)表示运输时间；(9)表示开始运输时间记为0；(10)表示实际交付时间不得超过交付期限；(11)表示实际运量不超过运输能力限制；(12)表示中转点中转能力限制；(13)表示节点间运输风险不可超过运输风险限制值；(14)表示中转风险不超过中转风险限制值。

1.4风险分析

本文只考虑运输风险与中转风险，其中风险可以表示为

R=Pζ。

(15)

式中R表示风险，P为危化品发生事故的概率，ζ为危化品发生事故造成的损失。其中，发生事故的概率可表示为

P=PkPcτ。

(16)

Pk为运输方式k发生事故的总体概率，该数值可以由全年交通事故统计所得数据求得。公路的事故概率为0.40×10-6次/km，铁路的事故概率为0.088×10-6次/km，水运的事故概率为0.028×10-6次/km，参考2012年中国统计年鉴。Pc表示事故发生后罐式集装箱破损的概率。τ为本地化因子，它反映该区域区别于其他区域诱使事故发生的环境影响因子，可以看作对道路(航道)等级、隧道、桥梁、疏散路网和其他应急设施的综合评价。

对于事故造成的损失，本文主要考虑事故发生后影响的人口数目，具体可表示为

ζ=4(σ)2ρ。

(17)

式中ζ表示液体危化品发生事故影响的人口数；ρ表示人口密度；σ表示发生事故的影响半径，影响半径参考表1，表1来源于佛兰德政府环保部门2009年报告(LNE，2009)。

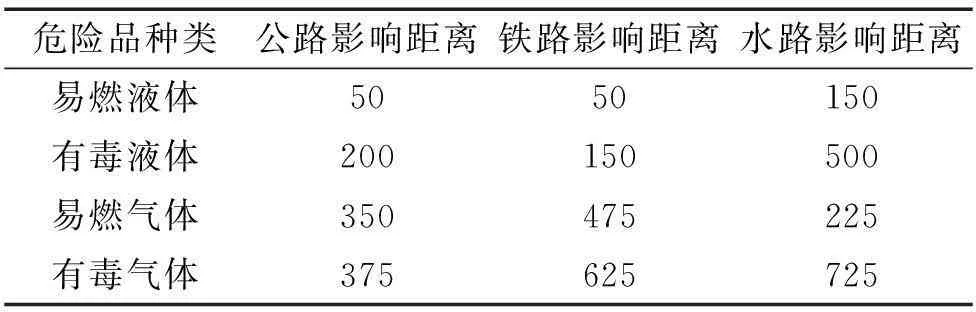
表1　危化品泄露影响距离

2基于二维欧氏距离客观赋权的模糊算法

对于多目标模型

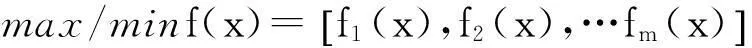
s.t.x∈f(x),

(18)

其求解算法如下[15]。

Step3:将多目标模型转化为单目标模型

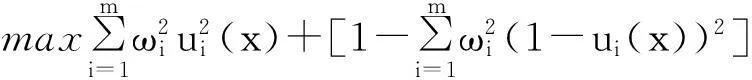
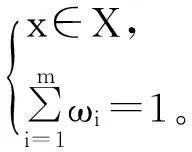
(19)

Step4:解单目标模型，构造拉格朗日函数

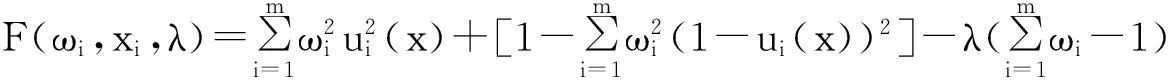
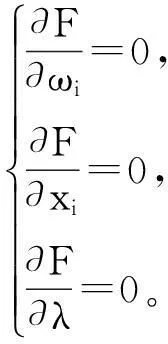
(20)

上述整个计算过程的实施通过Matlab软件完成。

3实例分析

危化品调运网络如图2所示，分别由供应点1、2，中转点3、4和需求点5、6组成。不同节点间有水路、铁路、公路可供选择。供应点1可提供油品30箱，苯2箱；供应点2可提供油品20箱，苯5箱；需求点5需要油品25箱，苯4箱；需求点6需要油品25箱，苯2箱。求满足需求的情形下，找到风险和成本整体最优的危化品调度方案。

已知公路、铁路、水路3 种运输方式的运费分别为0.4元/(t·km)、0.15元/(t·km)、0.05元/(t·km)，运速分别为60 km/h,40 km/h,20 km/h；交货期为48 h；租箱成本为200元/箱天(不足一天按一天算)；管理成本为50元/箱；发生事故后罐体破裂的概率为0.1；中转发生事故概率为0.2×10-6；运输能力限制为80箱，运输风险限制为0.5；中转能力限制为100箱，中转风险限制为0.1。表2、表3分别是运输过程和中转过程模拟数据。

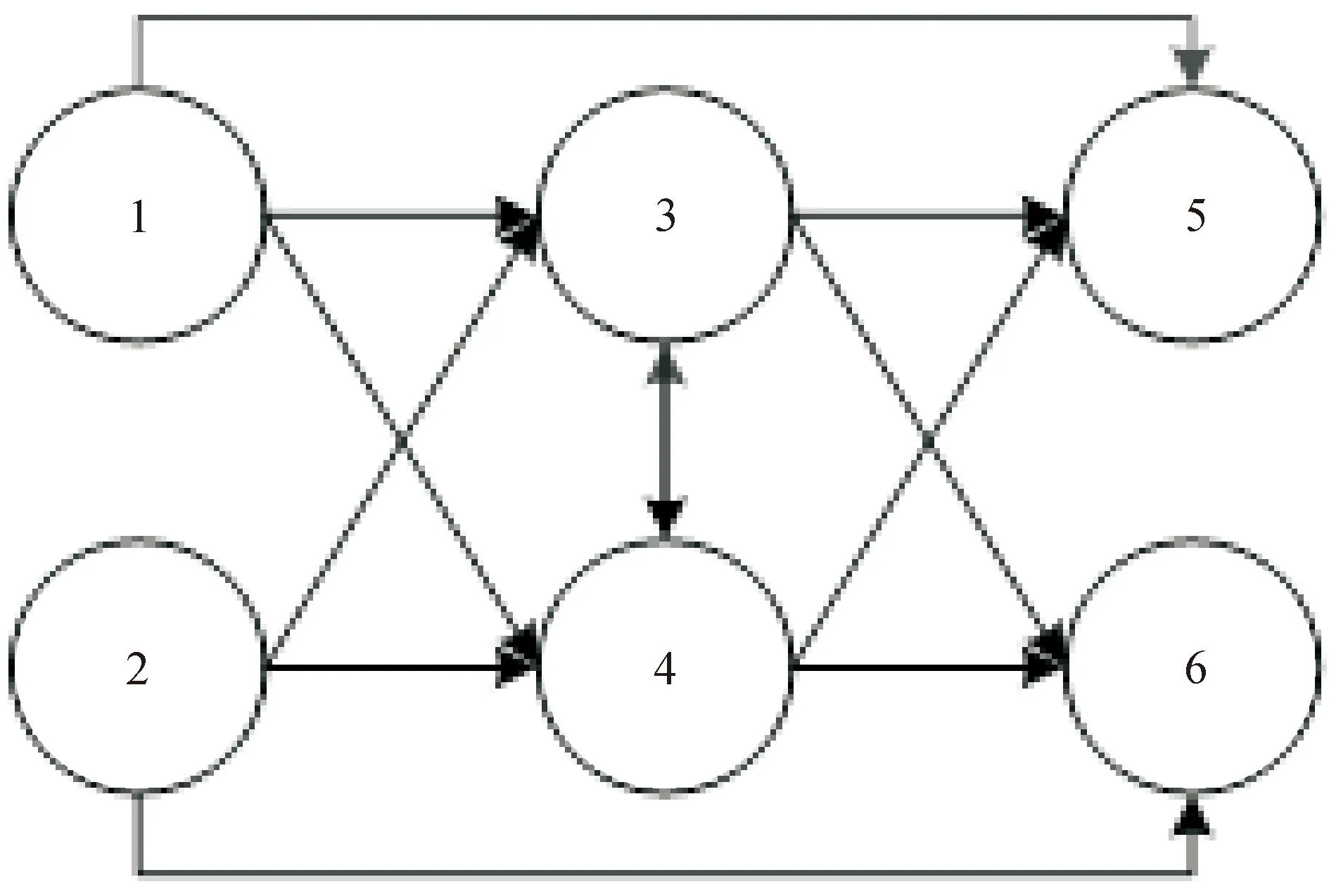
图2　算例联运网络

(i,j)距离/(km)本地因子人口密度/(人/km2)公路铁路水路公路铁路水路公路铁路水路1,3488585—36—800800—1,4681809—36—1000700—1,59881162—66—500800—2,36591169—44—800800—2,46188834333471200100010002,61743234210033467004003003,43493013925561500160012003,5450467—46—500600—3,6486998—36—600600—4,5782968—46—700600—4,6561900408448800700800

1)“—”表示节点间不考虑此种运输方式

表3　中转模拟数据1)

1)a/b/c中a的单位为h；b的单位为元；c的单位为人/km2

式(1)、(3)～(17)构成模型1成本最小，式(2)、(3)～(17)构成模型2风险最小，模型1、2求解结果见表4。

模型1求得最小成本是27.691 7万元，总风险是42.808 77×10-2。从调运方案可看出，由于水运成本最低，危化品特别是油品主要通过水路调运，而水-公联运既降低成本又避免单一水运由于时间过长增加调运风险。模型2求得最小风险是9.620 15×10-2，成本是151.418 6万元。调运方案显示危化品大多通过铁路或者公-铁联运调运，这主要因为一旦油品或苯发生泄露，水路的扩散速度远大于公路、铁路运输，并且水运事故救援反应慢代价高，影响人口远大于公路和铁路,为了保证调度安全，铁路成为首选，再通过公-铁联运缓解单一公路运输的调运风险。综上所述，多式联运可以弥补单一运输方式带来的不足，所得调运结果符合联运的风险分布。

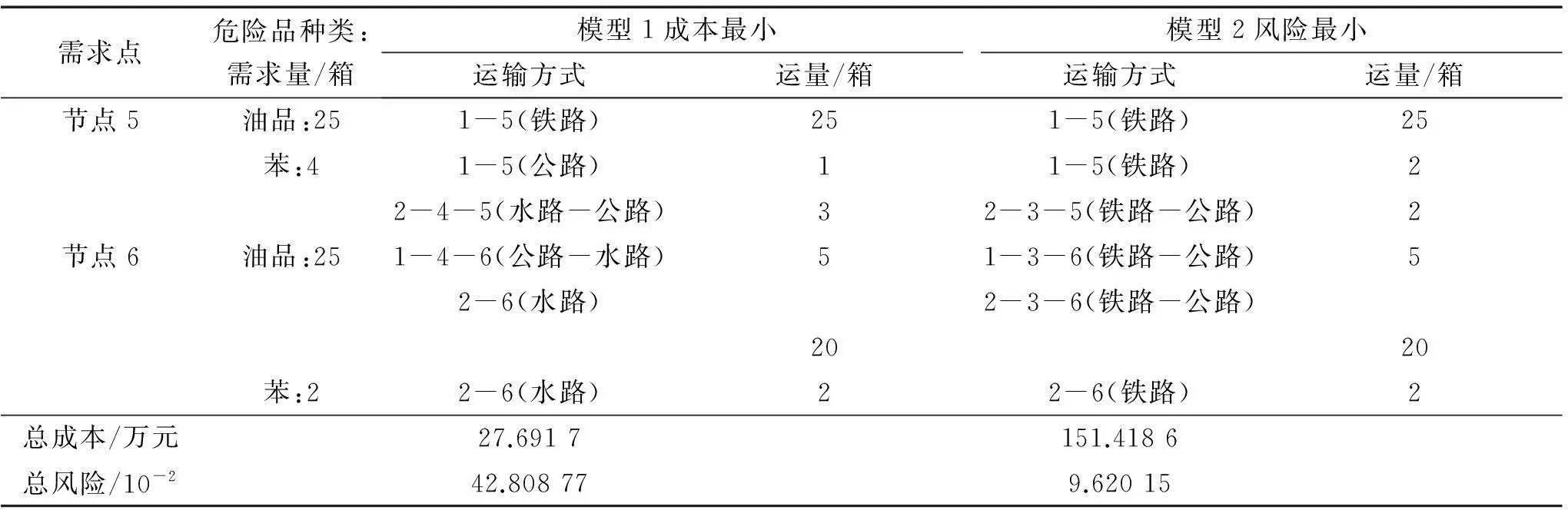
表4　单目标多式联运调运方案

式(1)～(20)构成模型3，求解结果见表5。

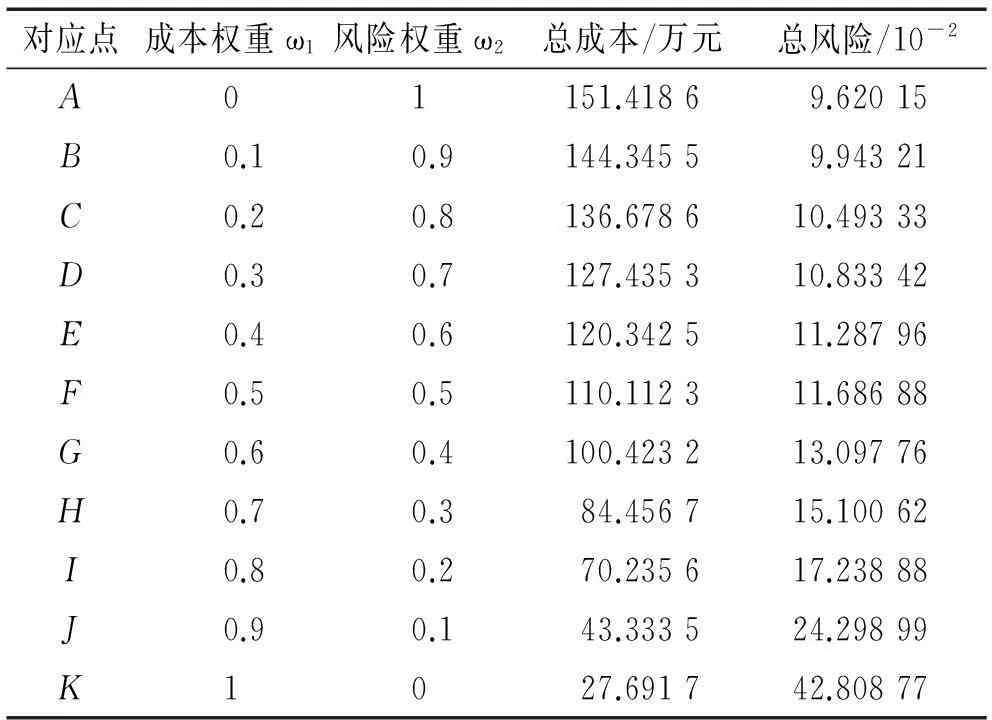
表5　不同权重下的成本-风险

表5给出了基于二维欧氏距离客观赋权的模糊算法在不同权值情形下的调度成本-风险值，其中权值ω1,ω2分别表示对成本、风险的重视程度。从表5可以看出，随着参数ω2值的变小，总风险在不断增加，成本在不断下降。根据表5中散点A-K,绘制得散点图3，K点对应调运方案成本最小风险最大，A点对应调运方案风险最小成本最高。物流企业一方面要保证运输安全，同时也要降低成本，就会权衡点A-K,找出相对较佳的调运方案。由图3看出，调运成本-风险的变化分三个阶段，第一阶段从点K到点J，成本增加约15.6万元就可降低风险约18.51×10-2，风险下降幅度最大；第二阶段从点J到点E，随着成本增加，风险下降幅度变小；第三阶段从点E到A，随着成本增加风险下降很少，趋近最小风险值。考虑到物流企业对安全的重视程度必定会赋予ω2更高的权值，同时要最大程度地降低成本，因此点E(ω1=0.4,ω2=0.6)对应的调度方案是相对较佳的，调运风险为11.287 96×10-2，调运成本为120.342 5万元，具体调度方案见表6。综上所述，该模型可以平衡成本与风险的关系，在调度风险可控范围内，最大程度的降低调运成本，得到成本与风险综合最优的调运方案。

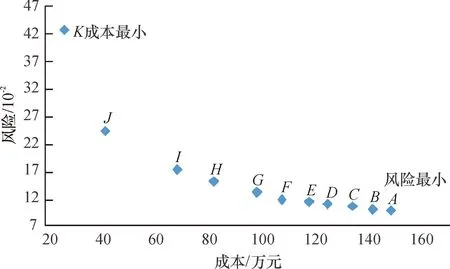
图3　基于权重的成本-风险图

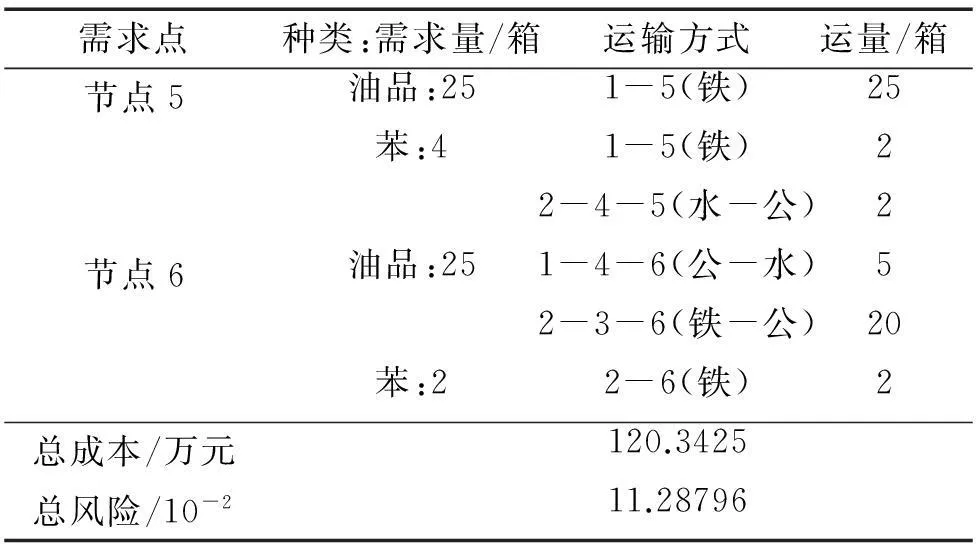
需求点种类:需求量/箱运输方式运量/箱节点5油品:251-5(铁)25苯:41-5(铁)22-4-5(水-公)2节点6油品:251-4-6(公-水)52-3-6(铁-公)20苯:22-6(铁)2总成本/万元120.3425总风险/10-211.28796

4结语

本文考虑到装卸搬运会加大危化品调度风险，特别的以罐式集装箱为载体，结合实际情况建立了不同品种危化品的多式联运调度模型，并利用二维欧氏距离客观赋权的模糊算法解决了基于成本和风险最小的多目标问题。结合算例验证，多式联运可以弥补单一运输方式带来的不足，所得调运方案成功地避开了风险较大的路段。并且该模型可以平衡成本和风险的关系，在风险可控范围内，最大程度地降低调度成本，这对物流企业安排调度计划有一定的借鉴意义。

参考文献：

[1]储庆中,张家应，谢之权.基于双层规划的危险品道路运输网络设计[J].重庆交通大学学报(自然科学版)，2010(2)：58-62.

CHU Qingzhong，ZHANG Jiaying，XIE Zhiquan. Road network design for hazardous materials transportation based on bi-level programming[J].Journal of Chongqing University(Natural Science)，2010(2)：58-62.

[2]种鹏云，帅斌. 一种基于决策者风险偏好的危险品运输路径优化问题研究[J].交通运输工程与信息学报，2012，10(1)：46-51.

CHONG Pengyun，SHUAI Bin. Research on routing optimization of hazardous material transportation based on risk preference of decision maker[J]. Journal of Transportation Engineering and Information，2012，10(1)：46-51.

[3]宋伟程，帅斌，陈钢铁.基于点危险源的危险品运输路径优化研究[J].中国安全科学学报，2012，22(2)：116-121.

SONG Weicheng，SHUAI Bin，CHEN Gangti. Dangerous goods transport path optimization based on point of hazard[J]. China Safety Science Journal，2012，22(2)：116-121.

[4]杨信丰，李引珍，何瑞春，等.多属性时间依赖网络的城市危险品运输路径优化[J].中国安全科学学报，2012，22(9)：103-108.

YANG Xinfeng，LI Yinzhen，HE Ruichun，et al. Route optimization for urban hazardous material transportation intime-dependent networks with multi-attributes[J].China Safety Science Journal，2012，22(9)：103-108.

[5]刘慧怡.危险品的多目标运输路径优化研究[J].武汉理工大学学报(交通科学与工程)，2013，37(3):585-588.

LIU Yihui. A multi-objectivetransportation path optimization research of dangerous goods[J]. Journal of Wuhan University of Technology，2012，22(9)：103-108.

[6]ASLAN H. Safe movement of hazardous materials through heuristic hybrid approach:tabu search and game theory application[J].Journal of Engineering Sciences，2008，14(3)：279-289.

[7]ROJEE Pradhananga，EIICHI Taniguchi，TADASHI yamada. ant colony system based routing and scheduling for hazardous material transportation[J]. Procedia Social and Behavioral Sciences，2010(2)：6097-6108.

[8]MOHDRAPIKSAAT，CHRISTOPHER P L Barkan. Generalized railway tank car safety design optimization for hazardous materials transport: addressing the trade-off between transportation efficiency and safety[J]. Journal of Hazardous Materials，2011，189：62-68.

[9]姜军，陆建.集装箱多式联运系统中各种运输方式最优组合模式研究[J].技术与方法，2008，27(4)：127-130.

JIANG Jun，LU Jian.Research on optimal transport mode combination in a multimodal transportation system of containers[J].Techniques and Methods，2008，27(4)：127-130.

[10]唐建桥，李新民，王慈光，等.集装箱多式联运组织优化模型及算法研究[J].交通与计算机，2008，26(3)：89-91.

TANG Jianqiao，LI Xinmin，WANG Ciguang，et al. Container multimodal transport organization optimization model and algorithm research[J]. Traffic and Computer，2008，26(3)：89-91.

[11]刘舰, 俞建宁. 多式联运运输方式选择的模型和算法[J].兰州交通大学学报，2010，29(1)：56-61.

LIU Jian，Yu Jianning. Intermodal transportation mode choice model and algorithm[J]. Journal of Lanzhou Jiaotong University，2010，29(1)：56-61.

[12]张鹏鸽，张煜，刘佳伟，等.不确定环境下公铁水多式联运决策研究[J].铁道运输与经济，2013，35(2)：41-45.

ZHANG Pengge，ZHANG Yu，LIU Jiawei, et al. Research on motor-rail-sea inter-model transport strategy under uncertain environment[J].Railway Transport and Economy，2013，35(2)：41-45.

[13]杨雪.考虑换装时间的集装箱多式联运路径优化问题研究[D].大连：大连海事大学，2013.

YANG Xue. Research on the optimal routes and modes selection in container multimodal transportation networks consider of the transshipment time[D].Dalian:Da Lian Maritime University，2013.

[14]BAUER J，BEKTAS T，CRAINIC T G. Minimizing greenhouse gas emissions in intermodal freight transport：an application to rail service design[J].Journal of the Operational Research Society，2010，61(3)：530-542.

[15]唐伟勤.大规模突发事件应急物资调度基本模型研究[D].湖北：华中科技大学，2009.

TANG Weqin.Study on the basic model of dispatching commodities of large-scale emergency[D].Hubei:Huazhong University，2009.

A Research on Multimodal Transportation Scheduling Model of Hazardous Chemical Materials in Tank Containers

HE Hongdi，XIE Jing，DING Yi，LIN Guolong

(Shanghai Maritime University， Logistics Research Center，Shanghai 200135，China)

Abstract：With the rapidly growing demands of hazardous chemical materials, transport accidents are more and more frequent. In order to reduce the risk of transportation and ensure the transportation safety, a research is conducted by connecting scheduling problems of hazardous chemical materials with multimodal transportation and the hazardous chemical materials packed in tank containers. A multimodal transportation scheduling model of hazardous chemical materials in tank containers is established based on the minimum cost and risk under a time constraint. At the same time, a fuzzy algorithm based on two-dimensional Euclidean distance is used to solve the model. The case study verifies that the application of multimodal transport to scheduling problem of hazardous chemical materials is beneficial to reduce risks and ensure safety of the scheduling. In addition, this method can reach the goal of minimizing cost within the scope of the controllable risk and it is a good reference for the logistics enterprise to do scheduling plan.

Key words：hazardous chemical materials；tank containers；multimodal transportation；scheduling model；fuzzy algorithm

中图分类号：U15

文献标志码：A

文章编号：1007-7375(2016)01- 0045- 06

doi:10.3969/j.issn.1007- 7375.2016.01.007

作者简介：何红弟(1980-)，男，陕西省人，副教授，博士，主要研究方向为交通流交通污染、绿色物流、低碳物流.

基金项目：国家自然科学基金资金资助项目(11302125，71301101)；上海教育委员会科研创新重点资助项目(11ZS1145)；上海市教育委员会科研创新重点资助项目(13YZ085)；上海市教委重点学科资助项目(J50704)

收稿日期：2014- 12- 26