航空公司飞机航线可更换单元两级库存控制方法

付维方, 卞　娇

(1.中国民航大学 航空工程学院, 天津300300; 2.中国国际航空股份有限公司 工程技术分公司, 北京 101312)



航空公司飞机航线可更换单元两级库存控制方法

付维方1, 卞娇2

(1.中国民航大学 航空工程学院, 天津300300; 2.中国国际航空股份有限公司 工程技术分公司, 北京 101312)

摘要：航空公司以维修基地和中央仓库两级库存保障飞机的航线可更换单元需求,同时规定高保障率以提供高航空服务质量，提出了保障率约束下的两级仓库最佳备件数量问题。本文首先通过航线可更换单元的失效数据以极大似然方法估计需求率，然后提出所有仓库总备件成本最小化为目标，备件综合保障率为约束的两级库存控制模型，最后采用边际分析法进行模型求解完成维修基地和中央仓库两级备件量的配置优化，实现航材资金占用量的最小化。通过实例验证表明采用此方法能够有效压缩库存规模，降低库存成本。

关键词：航线可更换件; 保障率; 极大似然方法; 两级库存控制; 边际分析法

航空器材价格高昂，其库存一直以来是我国航空公司巨大的负担。由于其不具有价值增值能力，降低航材库存是航空公司重要的成本控制工作。其中航线可更换件(line replacement unit, LRU)作为在航线上可更换的飞机组件由于其技术复杂、成本比重高，成为航材管理部门关注的重点。民用航空企业往往对航空器材采用两级库存的方式，在维修基地储备一定量的航材满足航线飞机维修的需要，保障飞机的有效使用，同时在运营总部建立中央航材库为各基地提供支援服务。在这种保障模式下，如何对高价LRU部件进行库存的管理和控制成为目前研究的主要问题。

上述库存管理的问题属于两级备件的管理问题，目前已有很多学者对其进行了研究。其中，Sherbrooke博士[1]对多级备件的库存优化技术基础理论进行了系统的论述，为多级库存的研究提供了基础；付兴方等[2]提出了在有限成本约束下的场站后订货数总和最小化的两级库存模型及算法；杜俊刚等[3]提出了基于可用度的航材二级库存控制模型；聂涛等[4]提出了有限购置费用条件下供应效能最大化的两级装备备件的库存优化方法；孙蕾[5-6]针对民用飞机的可用性提出了基于后订货数的备件控制模型和初始LRU的配置模型；周伟等[7]对武器装备贵重件两级供应关系进行研究，提出满足率约束条件下的初始备件购置费用优化模型和算法；王乃超等[8]提出以备件保障概率作为优化目标的备件库存多级模型。上述文献多以采购成本为约束条件，以可用性、后订货数量、保障概率作为目标函数，而且多应用在军用产品备件控制。对于民用航空企业，其往往以一定的航材保障率为先决条件确定两级最佳的库存数量。这与上述文献研究条件不同。杨建华等[9]针对复杂装备多种备件，提出以满足率为主要约束的多级库存控制模型，并用蒙特卡洛仿真的方法对模型进行了求解，但其只针对不可修部件，对于可修件没有提出解决方法。

本文以航空企业高价器材LRU为研究对象，基于失效数据运用采用极大似然估计方法确定其故障分布参数即需求率,运用Metric理论建立以综合保障率约束下的两级库存控制模型，以解决非成本约束下的飞机运行保障问题。其通过有效分配不同维修基地及中央仓库两级LRU备件数量以满足航空公司飞机运行保障的约束，同时使LRU备件成本最低。

1航材供应过程

航空公司通常根据自身运营管理特点在全国设置不同的基地，并为每个基地分配一定数量的飞机，由其负责这些飞机的维修和保障任务。基地往往具有自己独立的维修分部和资源保障分部。当飞机LRU出现故障时，将其拆下，由基地仓库提供LRU备件进行更换。拆下的故障LRU首先由基地进行维修；如果在基地无法修复，则将其提交给总部，由其实施外委维修或发往OEM(original equipment manufacturer)厂家直接维修，同时总部将为基地发送一个备用件；OEM厂家维修完毕后，将其发往中央仓库库房作为LRU备件；如果基地能够修复，则将修复后的LRU送至基地仓库作为可用LRU备件。整个过程如图1所示。

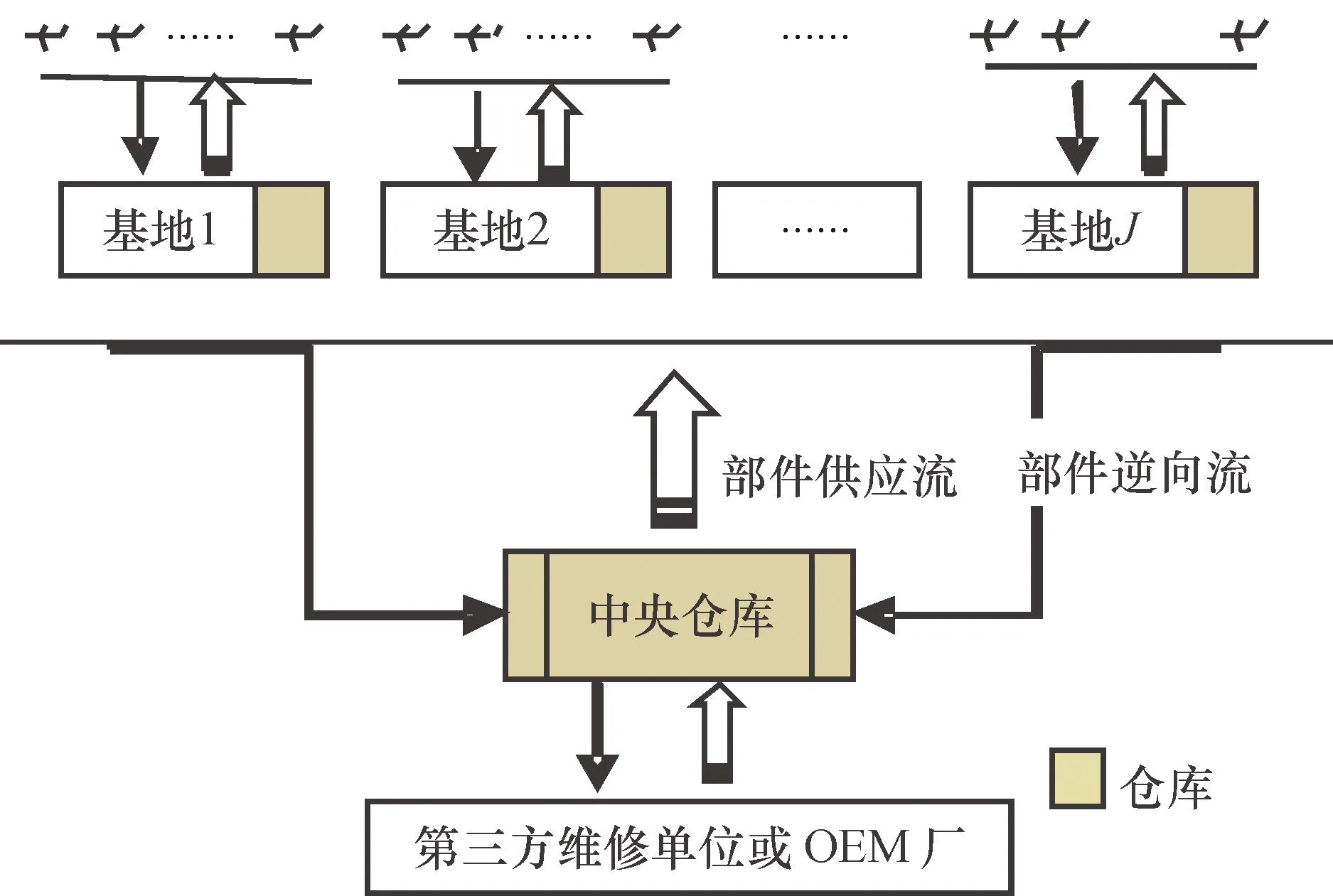
图1　部件的流动过程

2基地LRU需求率的确定

LRU结构复杂，由多元件组成，它在一定时期内的故障次数或更换需求往往建模为泊松过程[1]，也就是拆换间隔时间服从指数分布，其密度函数公式为

(1)

根据修理报告，获得LRU的每次拆卸时的使用时间，分别为t1,t2,…,tn，以极大似然估计方法[10]评估部件的年平均需求，似然函数为

(2)

ln)。

(3)

似然函数(3)的最小值即为似然函数(2)的极大值。对似然函数(3)求极值，得的极大似然估计值为

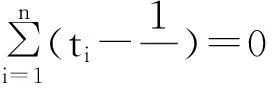
即

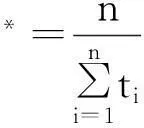
当获得单个装机位置LRU年平均需求后，则根据泊松分布的可加性获得维修基地的LRU年平均需求，计算方式为

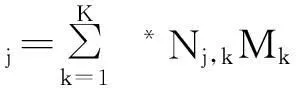
(4)

式(4)中，j表示基地序号；K表示机型数；Nj,k表示第j个基地直管的第k种机型的飞机数量；Mk表示第k种机型LRU的装机数量。

3两级库存模型的建立

3.1基本假设

为了简化问题的解决，进行如下假设。

1)各基地LRU需求互相独立，都服从泊松分布；

2)各基地仓库之间不存在横向的LRU供应，各基地除自身仓库之外只接受中央仓库的备件保障；

3)故障LRU基地能够维修的概率为r，外委或OEM维修的概率为1-r；

4)每一级都采用(S-1,S)库存策略；

5)需求处于稳态且不存在LRU报废情况；

6)各LRU具有相同的重要程度，进入中央仓库后会及时送修；

7)LRU不具有故障保留能力，出现故障需要及时更换。

3.2确定基地综合保障率

正常情况下每个基地仓库都存有一定量的LRU满足航线的故障更换需要，这里记为sj，当j为0时表示中央仓库。当航线存在一个需求时,就在基地仓库提取一个，这时基地库存就减少一个。飞机上更换下来的故障部件以rj的概率在基地维修，平均维修时间为Tj。但是由于基地的维修能力约束，还可能以1-rj的概率交由中央仓库送修，同时向中央仓库申请一个进行补充，申请与运输时间为Oj，送修的平均维修时间为T0。

中央仓库向基地提供补充的同时接收送修完毕的部件。这里对中央仓库平均年需求量为

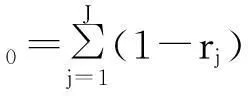
(5)

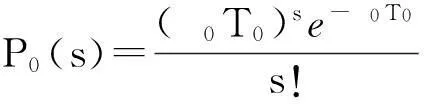
(6)

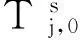
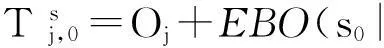
(7)

其中，EBO(s0|0T0)表示中央仓库有LRU为s0时的期望短缺数。

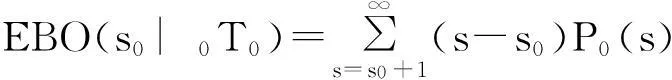
(8)

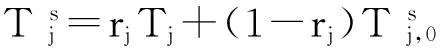
(9)

则基地j的LRU在修数量s的概率分布为

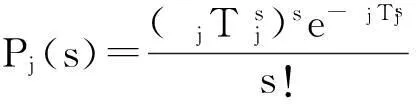
(10)

考虑到所有基地的保障能力后，可得综合保障率为

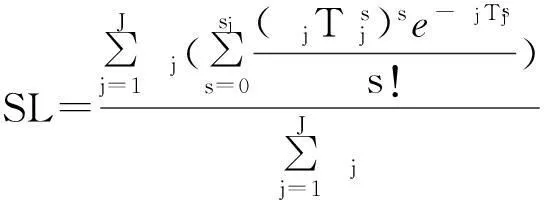
(11)

3.3模型建立

根据上述综合保障率模型，建立如下所示的部件优化模型。

minC(S)。

s.t.SL(S)>sl。

(12)

其中，sl表示企业设定的基地综合保障率目标;S表示各仓库初始库存LRU数量集合，C(S)为

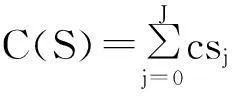
(13)

其中，c表示某LRU的单位购置成本。此模型表示在企业综合保障目标的约束下，如何调整各基地仓库和中央仓库LRU量使企业采购成本最低。

4模型求解

上述模型的求解可采用边际分析方法，用Δj作为单位效能因子，其计算方法为

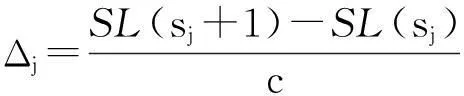
由于

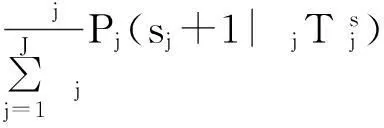
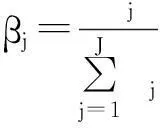
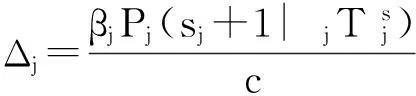
(14)

Δj表示某LRU在基地j增加一个单位时其综合保障概率的单位成本变化率。边际方法就是在每轮计算中确定不同基地的Δj，选择最大的Δj作为优先增加单位LRU的基地。然后进入下一轮继续计算Δj和选择，直至达到综合保障率指标。具体算法见图2。

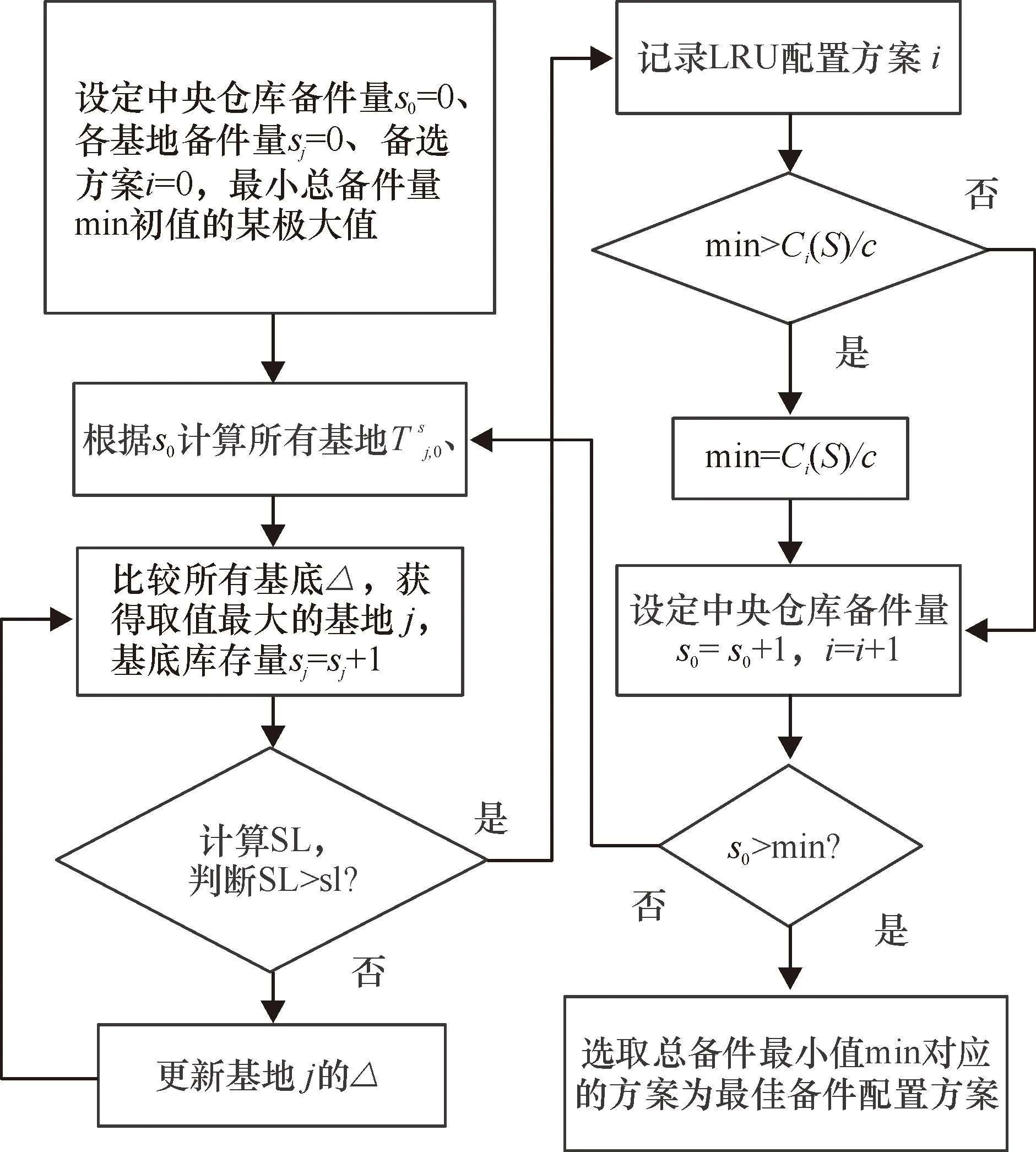
图2　模型求解过程

5实例分析

某航空公司在全国设定了4个维修基地并具有附属的航材库，公司总部建立了中央航材库满足各基地航材的需求。已知此航空公司只运营一种机型，基地1直管飞机15架，基地2直管飞机25架，基地3直管飞机10架，基地4直管飞机16架。每架飞机某LRU装机数量为3，根据修理报告得知其寿命数据如表1所示。

此类LRU平均送修周期为45 d，所有基地维修周期平均都为15 d，单价为93 556美元。当基地向中央仓库请求航材时采用空运的方式运输，所以所有LRU向基地的运输时间均为1 d。LRU故障时由基地维修的概率为0.2。公司此LRU综合保障率设定为0.95。

由于飞机的使用寿命单位为飞行小时，根据飞机的日利用率8飞行小时/d转换为日历日。获得此部件的失效率为0.000 189 796个/d。表2给出了不同基地的计算得到相关参数。

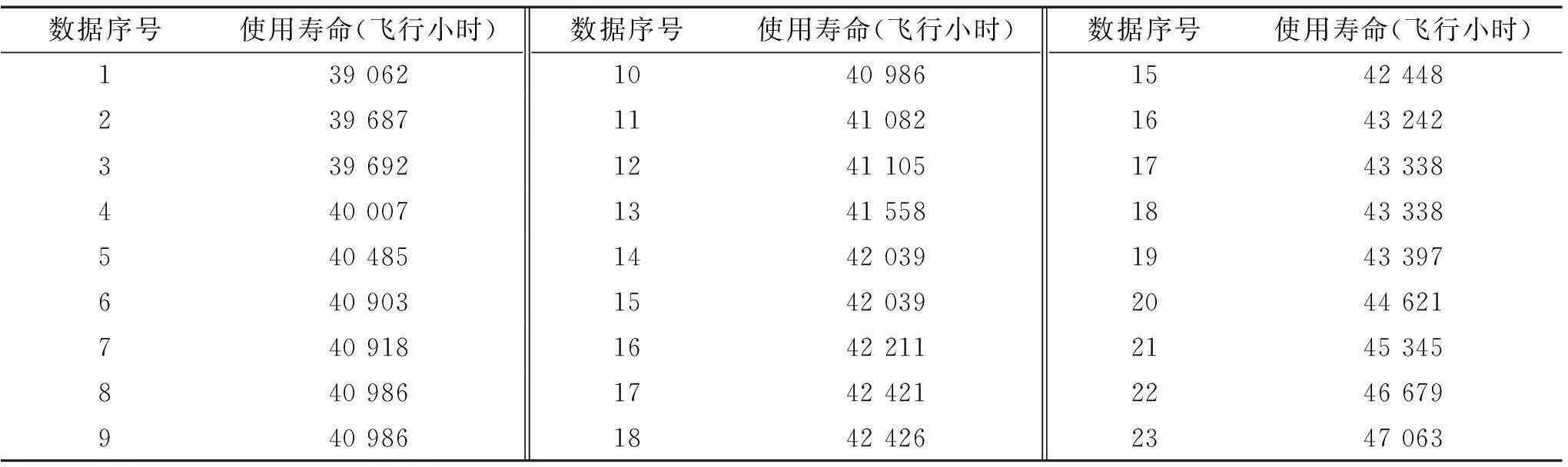
表1　修理报告寿命数据

表2　不同基地的相关参数

根据以上信息，利用式(10)～(14)按照图2的逻辑计算得出结论，如表3所示。当中央仓库LRU为0时，在基地1、3、4各存贮1个LRU，在基地2设置2个LRU，就能使LRU的综合保障率达到需要的95%以上，这样可以在下一步的迭代计算中总LRU量以5作为约束条件。以此类推，这样将大大减少计算范围，提高求解速度。

表3　满足保障需求的备件方案

通过表3可知，如果以95%作为航空公司某LRU的综合保障目标，只要在中央仓库采购2个LRU备件，在基地2采购1个LRU备件即可，总LRU备件成本为280 668美金。

6结论

根据LRU的修理报告获得其可靠性数据并以此采用极大似然估计对基地的航材需求率进行计算，针对航空公司器材管理模式提出LRU的两级库存控制模型及其求解算法。本模型以企业设定的基地综合保障率为约束，以总备件成本最小化为目标，符合航空企业的运营实际具有一定的实用性。由于在分析时只考虑单一件号的LRU，未对飞机机载的所有LRU综合考虑，也没有考虑各基地间横向供应问题，因此下一步应对模型及算法进一步改进以适应企业所有LRU综合库存控制的要求。

参考文献：

[1]SHERBROOKE C C. Optimal inventory modeling of system: multi-echelon techniques[M]. 2nd ed. New York: Springer, 2004.

[2]付兴方, 李继军, 李宗植. 基于两级供应关系的可修复航材存储策略模型研究[J]. 系统工程理论与实践,2004, 24(2): 111-115.

FU Xingfang, LI Jijun, LI Zongzhi. A stock strategy model for restoring air materiel based on the two-level providing condition[J]. Systems Engineering-Theory & Practice, 2004, 24(2): 111-115.

[3]杜俊刚, 杜鑫, 何亚群. 基于飞机可用度的航材二级库存优化配置. 兵工自动化,2009, 28(1):39-44.

DU Jungang, DU Xin, HE Yaqun. Premium allocation of spare inventory in two-echelon supply system based on aircraft operational availability[J]. Ordnance Industry Automation, 2009, 28(1):39-44.

[4]聂涛, 胜文, 王晗中. 装备备件两级闭环供应链库存优化与分析[J]. 系统工程理论与实践,2010, 30(12):2309-2314.

NIE Tao, SHENG Wen, WANG Hanzhong. Optimizing and analyzing two-echelon closed loop supply chain storage system for equipment spare part[J]. Systems Engineering-Theory & Practice, 2010, 30(12):2309-2314.

[5]SUN Lei, ZUO Hongfu. Multi-echelon inventory optimal model of civil aircraft spare parts[C].2010 Chinese Control and Decision Conference. Xuzhou: IEEE, 2010:824-828.

[6]孙蕾 左洪福.基于METRIC 的民机初始备件数量确定及配置模型[J]. 中国机械工程, 2013,24(23):3200-3204

SUN Lei, ZUO Hongfu. Optimal allocation modeling for initial spare parts of civil aircraft based on METRIC[J]. China Mechanical Engineering, 2013,24(23):3200-3204

[7]周伟, 刘亚杰, 郭波, 等. 基于两级供应关系的武器装备贵重件初始配置模型[J]. 系统工程理论与实践,2011, 31(6):1056-1061.

ZHOU Wei, LIU Yajie, GUO Bo, et al. Initial configuration model about the valuable parts of weapon system based on two-class supply relationship[J]. Systems Engineering-Theory & Practice, 2011,31(6): 1056-1061.

[8]王乃超, 康锐. 基于备件保障概率的多级库存优化模型[J]. 航空学报, 2009.30(6):1043-1047

WANG Naichao, KANG Rui. Optimization of multi2echelon repairable item inventory systems with fill rate as objective[J]. Acta Aeronautica et Astronautica Sinica. 2009.30(6):1043-1047

[9]杨建华, 宋扬. 基于备件满足率的多级备件库存模型研究[J]. 工业工程与管理,2014,19(4):8-14

YANG Jianhua, SONG Yang. Research of multi-echelon spare parts inventory model based on fill rate constraint[J]. Industrial Engineering and Management, 2014,19(4):8-14

[10]RAUSAND M, HØYLAND A, System reliability theory: models, statistical methods and applications[M]. Hoboken, New Jersey: John Wiley, 2004.

[11]MUCKSTADT J A. Analysis and algorithms for service parts supply chains[M]. New York: Springer, 2004.

An Approach to Two-echelon Inventory Control of Aircraft LRU for Airline

FU Weifang1, BIAN Jiao2

(1.School of Aviation Engineering, Civil Aviation University of China, Tianjin 300300, China;2. Engineering Technics Branch, Air China Limited, Beijing 101312,China)

Abstract：Airlines meet maintenance requirement of line replacement unit (LRU) with two-echelon supply pattern by base warehouse and central warehouse and set high fill rate to support airplane operation. Under this situation, it raises a problem as to how to decide LRU stock level in different base and central warehouses. Firstly, the requirement rate of LRU is calculated by Maximum Likelihood method using its failure data. Secondly, a two-echelon inventory control model is established to optimize total inventory costs under the constraint of joint fill rate. At last, a marginal analysis algorithm is designed to solve this model. An example is given to show that this approach is effective and reduces inventory cost.

Key words：line replacement unit; fill rate; Maximum Likelihood ; two-echelon inventory control; marginal analysis algorithm

中图分类号：V37

文献标志码：A

文章编号：1007-7375(2016)01- 0061- 05

doi:10.3969/j.issn.1007- 7375.2016.01.009

作者简介：付维方(1977-)，男，天津市人，讲师，硕士，主要研究方向为数字化维修、决策支持系统.

基金项目：国家自然科学基金委员会与中国民用航空局联合资助项目(U1233107)

收稿日期：2015- 03- 03