微网中双向DC-AC变流器的性能优化控制
杨 刚 杨奇逊 张 涛 刘 树 张 恒
(1.新能源电力系统国家重点实验室(华北电力大学) 北京 102206
2.北京四方继保自动化股份有限公司 北京 100084
3.国网北京经济技术研究院 北京 102209)
微网中双向DC-AC变流器的性能优化控制
杨刚1杨奇逊1张涛2刘树2张恒3
(1.新能源电力系统国家重点实验室(华北电力大学)北京102206
2.北京四方继保自动化股份有限公司北京100084
3.国网北京经济技术研究院北京102209)
摘要为解决用于直流微网与交流电网相连的双向DC-AC变流器因受到交直流双侧母线电压谐波的影响而导致的交流并网电流波形质量恶化等问题,首次推导了考虑交直流双侧电压谐波情况下的DC-AC变流器交流并网电流的表达式,揭示了交直流双侧电压谐波影响的本质和特征。同时引入DC-AC变流器交流侧并网电流dq轴分量的比例-积分-双重复控制策略以抑制上述影响。进一步针对数字化系统中存在的系统采样频率与基波频率比为非整数造成重复控制器增益显著衰减的问题,提出基于对期望采样数据进行局部线性插值的重复控制器增益提升方法,以增强重复控制器对交流电网电压谐波的抑制性能。详细的仿真和实验结果证明了理论分析以及所提交流并网电流波形质量优化控制策略的正确性和有效性。
关键词:微电网DC-AC变流器双侧电压谐波重复控制
0引言
微网作为一种分布式发电源的集成互联形式,因其具有无需考虑配电线路的涡流损耗以及线路吸收的无功能量、较高的控制灵活性和可靠性等优点,在分布式可再生能源发电领域显示出了巨大的发展潜力和广阔的应用前景[1- 8]。
目前的微网已经发展为交流微网、直流微网以及交直流混合微网,可以更加灵活地接入具有不同输出电能形式的微源以及负载。作为保证电能持续传输并且维持较高电能质量的关键装置,交直流微网互联以及联网型直流微网中用于连接交流电网的双向DC-AC变流器的控制问题得到了广泛关注[9-11]。图1所示为联网型直流微网的典型结构,当直流母线带动单相交流逆变电源时,会产生周期波动(即直流电压谐波),而交流母线电压也会存在低次谐波。通常DC-AC变流器采用基于同步旋转坐标变换的矢量控制策略。当采用比例积分(Proportional Integral,PI)控制器对并网电流的同步旋转坐标系下的dq轴分量进行控制时,由于PI控制器不具备抗周期扰动的能力,因此造成交直流双侧电压谐波均会在并网电流中产生低次谐波,进而造成对交流电网电压的谐波污染。
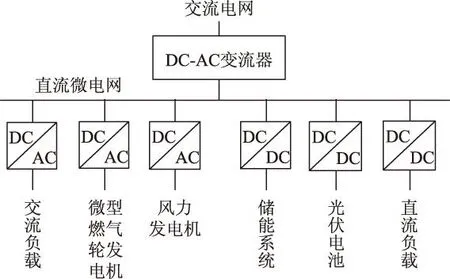
图1 典型联网型直流微电网简化结构Fig.1 Simplified structure of grid-connected DC microgrid
目前对DC-AC变流器交流电网电压谐波以及不平衡条件下的电流控制问题进行了大量的研究工作,如基于正负序电压矢量分离的双旋转坐标系的矢量控制策略[12-14]以及直接功率控制策略[15]等。而在抑制交流电网谐波方面,一种方案是引入谐振控制器,通过在谐波频率处产生较大增益来抑制谐波[16,17]。由于一个谐振控制器只能消除某一次谐波,因此在谐波次数分布较广时需要较多的谐振控制器,以致系统结构复杂。另一种方案是加入重复控制器,利用其在整数倍次频率处具有较大增益的特点来实现对多次谐波的抑制[18-20],并针对重复控制器存在的动态响应较慢、稳定性较差等缺点进行了一些改进[21-23]。
综上所述,现有文献中主要针对交流电网电压谐波的抑制开展了相应的研究工作,而对于同时解决DC-AC变流器交直流双侧电压谐波影响方面的研究鲜见报导,在机理分析以及解决方案方面均有待开展深入细致的研究工作。
本文首次分析了交直流双重电压谐波对用于双级式变流器以及直流微电网和交流电网互联的DC-AC变流器交流侧并网电流的影响,进而引入比例积分结合双重复控制(Proportional-Integral-Dual Repetitive Control,PI-DRC)策略抑制交直流双侧电压谐波的影响。进一步提出在采样频率与电网基波频率的比值为非整数时重复控制器的增益提升方法,以提高所提出的方案对交直流电压谐波的抑制能力,同时优化交流并网电流的波形质量。
1交直流双侧电压谐波对并网电流的影响分析
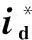
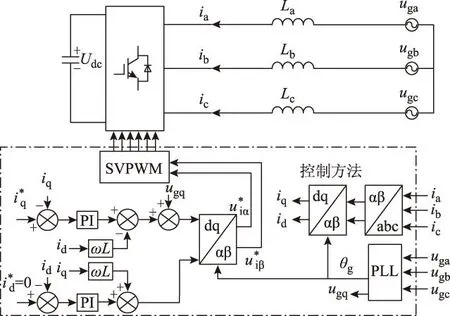
图2 基于矢量控制的DC-AC变流器原理结构Fig.2 Principle diagram of DC-AC converter based on vector control
同步旋转坐标系下DC-AC变流器的s域平均模型为
(1)
式中,ugd为交流电网电压d轴分量;uid、uiq分别为变流器输出电压的dq轴分量;mid、miq分别为uid、uiq忽略高次谐波的幅值调制比。
下面以q轴电流为例,分析交直流双侧电压谐波的影响。在DC-AC变流器中通常加入前馈解耦环节以实现dq轴电流的解耦控制。采用PI控制器的q轴并网电流分量控制环的闭环传递函数可以表示为
(2)
直流电压的扰动传递函数为
(3)
交流母线电压的扰动传递函数为
(4)
式中,Udc、Miq分别为所选取的稳态工作点对应的直流电压和q轴幅值调制比;上标“^”代表各变量在s域下的小信号扰动;KqP和KqI分别为q轴电流环的比例和积分系数。
首先分析直流电压扰动的影响,这里采用求取闭环系统稳态误差的方法来实现。在直流母线带动单相逆变负载时,直流电压会存在单相逆变负载二倍频的周期波动,假设
(5)
由于直流电压扰动为正弦量,需要采用级数求解法来获得其稳态误差。由自动控制理论可知,扰动稳态误差的级数表达式为
(6)
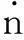
(7)
式中,Φn(s)为扰动传递函数。对于本文所述DC-AC变流器,Φn(s)=Φiudc(s)。
根据式(3)、式(5)~式(7),求得并网电流q轴分量在直流电压扰动下的稳态误差表达式。为简化分析,只给出前三项,即
(8)
(9)
式中,KdP和KdI分别为d轴电流环的比例和积分系数。
在得到直流侧电压的周期波动对DC-AC变流器并网电流影响表达式的基础上,进一步按照上述思想求取变流侧电压谐波对并网电流的影响。考虑电网电压存在5、7、11次谐波时,其dq轴分量扰动可以表示为
(10)
式中,Ugdm5、Ugdm7、Ugdm11和φg5、φg7、φg11分别为5、7、11次谐波的幅值和初始相位;φg1为电网电压基波矢量的初始相位。
根据式(4)~式(7),求得并网电流q轴分量在交流电网电压扰动下的稳态误差表达式为
(11)
式中
由上式可知,电网电压的k次谐波会在q轴上产生k-1的电流谐波。
同理,可以求得并网电流d轴分量在交流电网电压扰动下的稳态误差表达式为
(12)
式中
若令KdP=KqP、 KdI=KqI、 Mid=Miq, 将所得到的并网电流dq轴分量的稳态误差表达式经过同步旋转坐标系逆变换后,得到a相并网电流的谐波表达式为
(13)
由上述分析可知,当并网电流dq轴分量采用PI控制器时,直流电压存在的周期波动会在交流并网电流中产生2ωd±ω次谐波,而电网电压谐波会产生相同频率的谐波。上述两方面造成并网电流中产生较大谐波,恶化了并网电流波形质量。
2并网电流的PI-DRC及其改进
2.1并网电流的PI-DRC控制策略
为解决交直流双侧的电压谐波在电流dq轴分量上均会产生的偶数次谐波的问题,本文引入PI结合两个RC电路的电流控制策略。其中PI控制器用于直流分量的闭环控制,而RC用于谐波抑制。理论上,ωd=ω,但是实际系统中ωd通过软件控制,可以认为不变,而电网角频率受到实际供电条件的影响,会发生变化,因此采用两个RC进行抑制。其基本思想是:将PI控制器和两个RC相结合用于并网电流d、q轴分量的控制。其中第一个重复控制器(RC1)用于实现直流电压谐波的抑制,而第二个重复控制器(RC2)用于电网电压谐波的抑制,两个RC具有相同的结构,只是延时常数不同。图3给出了相应的并网电流闭环控制框图,点划线框内的环节为重复控制器[16]。图中,e-sTRC1代表等效延时环节,TRC1为重复控制器的固有延时常数;KRC1为其比例系数;Q1(s)为重复控制器外加的低通滤波器,用于提高鲁棒性和稳定性;N1(s)用于补偿延时环节的相位滞后和增益;GPIq(s)为比例积分控制器的传递函数;GRC2(s)为RC2的传递函数。
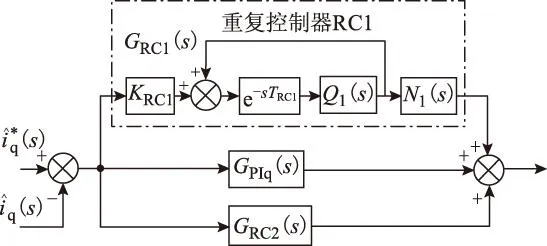
图3 并网电流q轴分量的PI-DRC控制策略原理框图Fig.3 Schematic of PI-DRC of q-axle component of grid current
(14)
对于Q1(s), 采用一阶零相移滤波器,为
(15)
对于N1(s), 选择纯超前补偿器,其传递函数为
N1(s)=esΔT
(16)
式中,ΔT为超前补偿时间;TRC1=π/ωd。而对于RC2的各项参数,应有TRC2=π/ω,其余参数与RC1相同。
下面分析采用上述方案后的系统控制性能。加入RC后电流环的闭环传递函数为
(17)
eiq(t)=
(18)
由式(18)可知,采用所提出方案的并网电流稳态误差为零,说明仍然能够实现并网电流的无静差控制。
新的直流电压扰动传递函数为
(19)
而新的电网电压扰动传递函数为
(20)
由前述分析可知
农村地区在实行乡村振兴政策的进程中,面临着包括农村金融体制完善性缺失、金融风险化解机制缺失和资源配置不均衡等方面的问题。在这样的背景下,就需要我国政府通过提升农村金融服务管理体系的科学性和创建完善的农村金融风险承担和应对机制的方式,来实现农村地区经济的发展,进而促进整个中国经济的发展,为中国人民享受更好的生活品质而努力。
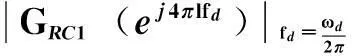
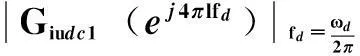
式中,l=0,1,2,…。 即在4πfd、4πf及其整数倍处的幅值增益为零。
2.2采样频率/扰动信号频率比为非整数时的改进方案
在所提出的PI-DRC策略的基础上,进一步分析电网电压频率变化对RC性能的影响及其解决方案。令采样频率为fs,有RC2中的延时常数为
(21)
式中,NRC2为采样频率与拟抑制信号频率的比值,即频率比。当TRC2/Ts为整数时,RC的实际固有延时常数与其期望值相等;当TRC2/Ts为非整数时,由于NRC1只能取为最接近频率比的整数,导致重复控制器的延时常数存在偏差。实际系统中,由于交流电网频率存在波动和偏差,TRC2/Ts的值无法始终为整数,从而造成NRC2与实际的TRC2/Ts存在差异。在用于直流母线与交流母线互联的DC-AC变流器中,由于其功率相对较大,功率器件的工作频率通常都选得较低,系统采样频率亦随之降低,从而也造成上述差异较大。下面首先分析延时常数偏差对RC2增益的影响,进而提出增益提升方法。
由重复控制器的原理可得其标准形式为
(22)
定义
(23)
(24)
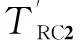
(25)
对应实际电网的变化为
=[-3.4%, 3.2%]
(26)
实际电网频率受随机性负载的影响变化范围会超过上述范围,从而导致重复控制器的增益下降,也因此降低了交直流双侧电压谐波的抑制能力。进一步绘制RC2的伯德图及各频率点的幅值增益如图4所示。由此图可知,二倍频的幅值增益由140 dB降低到20 dB,说明延时常数的偏差造成重复控制器的幅值增益降低明显,从而导致其对电压谐波的抑制效果明显降低。
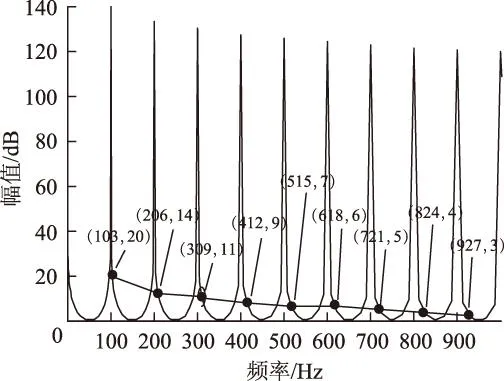
图4 延时常数存在偏差时的RC伯德图Fig.4 Bode diagram of RC with error delay constant
现有文献中,给出了一些RC对被控对象的频率变化适应性的解决方案,如对RC中的延时常数根据被控对象的频率变化进行在线调整等[15-17]。但是上述方案并不能解决由于系统的数字化实现方案带来的采样频率与被控对象频率的比值为非整数时的控制性能恶化的问题。
下面提出一种基于线性插值对实际采样值进行在线估计的方法以增强RC的幅值增益,如图5所示。即通过对期望采样点相邻的两个采样值进行线性插值运算,进而获得期望采样点的估计值,从而提升其幅值增益。线性插值算法的标准公式为
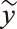
(27)
(28)
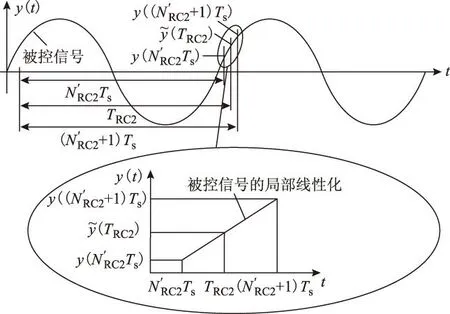
图5 采样点信号线性插值原理示意图Fig.5 Schematic of linear interpolation algorithm of sampling signal

(29)
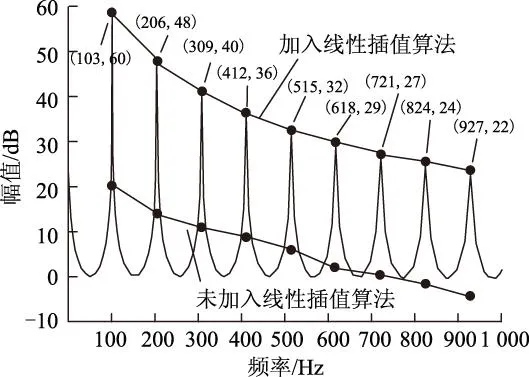
图6 加入线性插值估计算法的重复控制器伯德图Fig.6 Bode diagram of repetitive controller with linear interpolation estimating algorithm
3仿真结果及分析

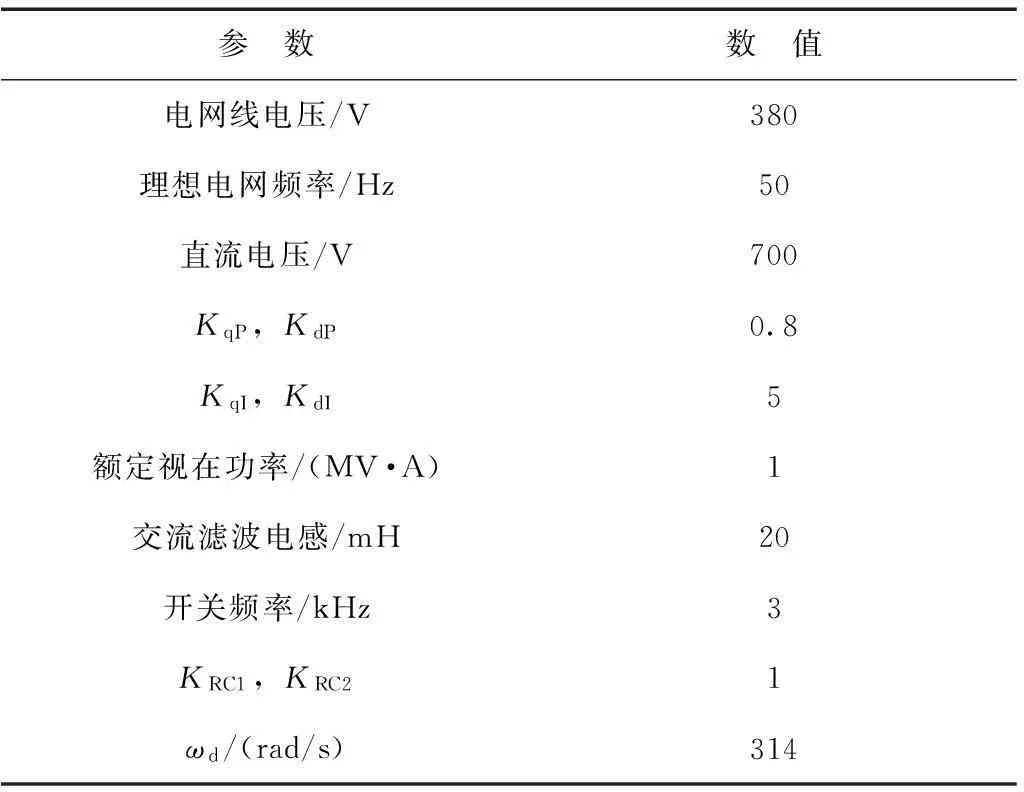
表1 仿真系统参数及电网数据
图7为在表1给出的仿真参数下,应用传统PI控制以及理想条件下的PI-DRC控制的DC-AC变流器输出的仿真波形。其中,图7a给出了采用传统PI控制器的仿真波形。由图可知,在传统PI控制下,DC-AC变流器输出的交流并网电流产生了明显畸变,其A相并网电流频谱显示并网电流包含较高含量的3、5、7、11次等谐波,同时总电流谐波畸变率(Total Harmonic Distortion,THD)达到6.47%,已经超过了相应的并网标准。图7b给出了在理想条件下,采用PI结合传统RC的控制方案的仿真结果,由并网电流仿真波形图以及A相电流的频谱分析可以看出,并网电流各次谐波均得到了有效抑制,电流THD下降到2.98%。
图8a给出了电网电压变为51 Hz时采用PI结合传统RC的控制方案的仿真结果,此时由于RC的延时时间保持不变,导致谐波抑制能力下降,电流THD达到5.01%。而图8b给出了采用PI结合改进RC方案的

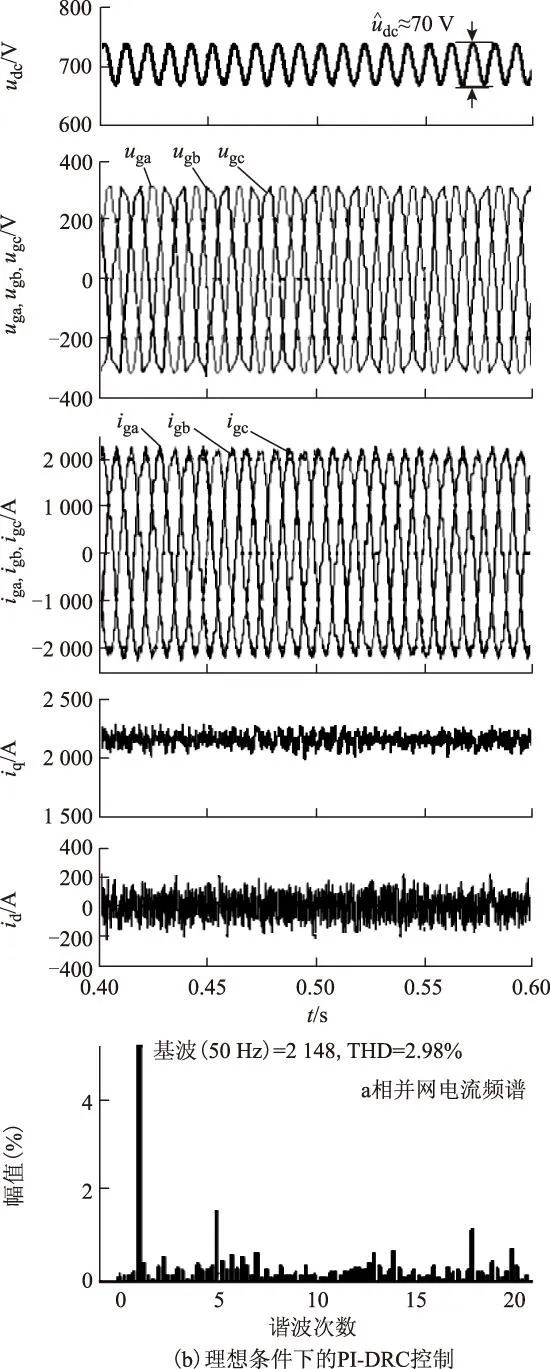
图7 DC-AC变流器仿真波形Fig.7 Simulation waveforms of the DC-AC inverter
仿真结果,由于RC的延时时间根据电网频率进行相应的调整,从而保持了较高的谐波抑制能力,电流THD下降到3.12%,与图7b给出的理想条件下的电流THD接近。说明所提出的改进方案实现了交直流双侧电压谐波条件下的并网电流波形质量优化。最后,给出了并网电流阶跃变化时的仿真结果如图9所示。在不同并网电流基波幅值的情况下,均获得了较好的谐波抑制效果,说明具有较好的电流幅值适应性,而其动态响应较快,整个过程电流波形保持平稳。
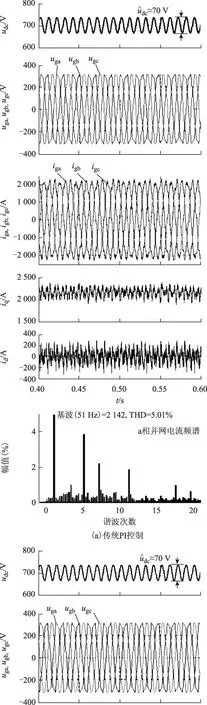
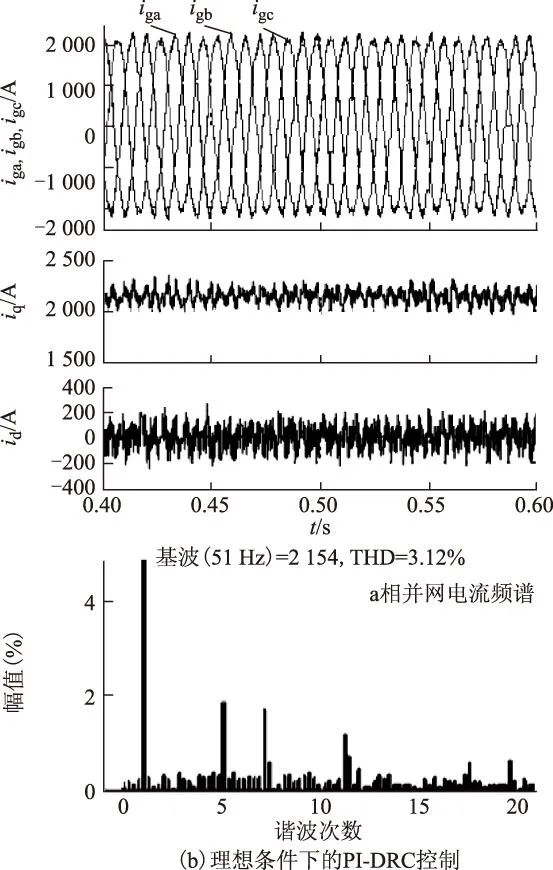
图8 电网频率变化时的DC-AC变流器仿真波形Fig.8 Simulation waveforms of the DC-AC inverter under variation of grid frequency conditions
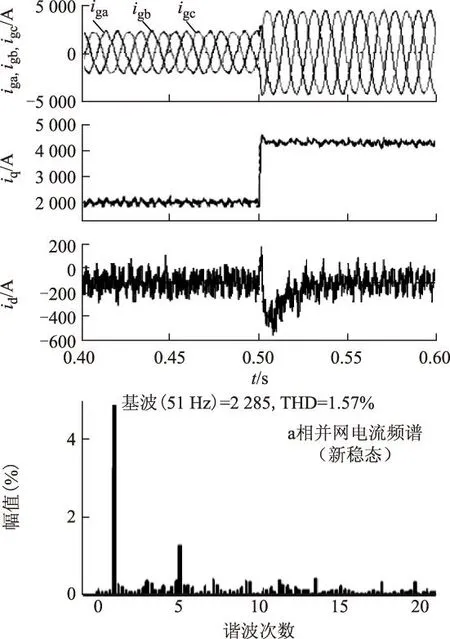
图9 DC-AC变流器阶跃响应仿真波形Fig.9 Simulation waveforms of step response of DC-AC inverter
4实验验证
为进一步验证本文的理论分析结果和所提出改进的重复控制策略在变流器交直流双侧电压谐波影响下的性能,搭建了基于DSP TMS320F28335的实验平台进行实验验证,实验参数见表2。由于很难在交流电网电压中直接注入低次谐波,因此只对直流电压波动下的采用PI调节器和所提出的改进PI-DRC两种情况下的系统性能进行实验验证。为模拟直流电压的周期波动,使变流器工作于整流状态,同时直流侧连接单相交流逆变电源,其处于直流电压、负载电流双闭环工作状态,由此会在直流电压中产生100 Hz的周期波动。
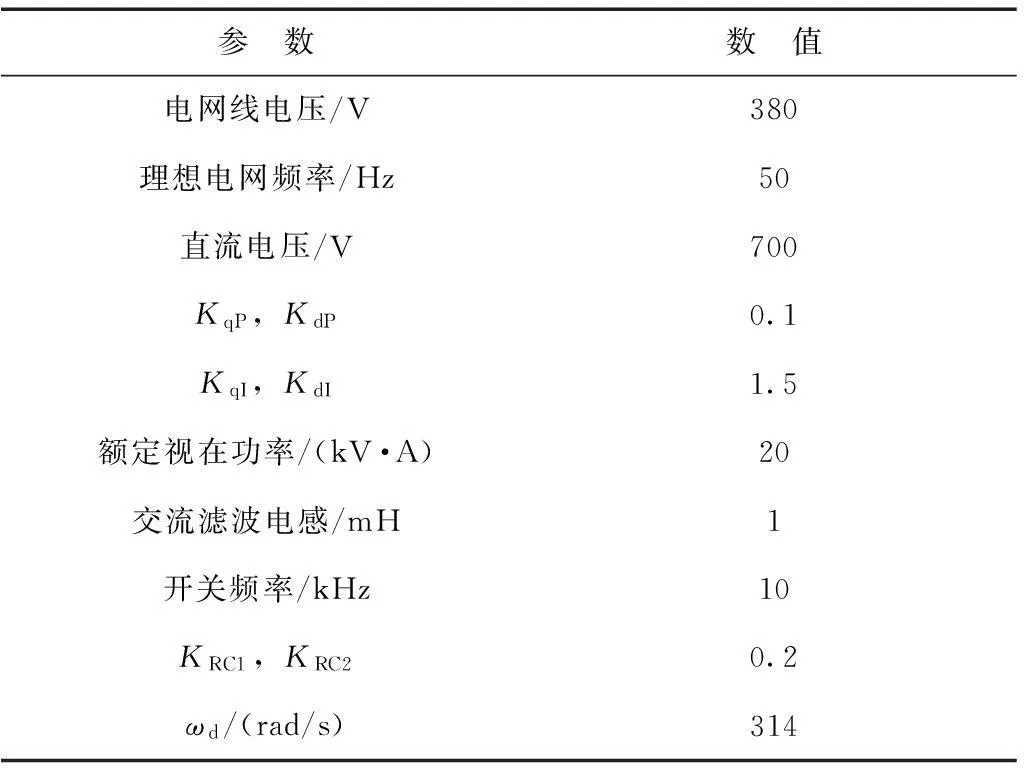
表2 实验平台系统参数
图10a给出了10 kV·A单相交流逆变电源的直流电压波形及其频谱和单相负载电流iload波形,由图10a可知,在单相逆变负载的作用下,直流电压存在明显的周期波动,主要分布在负载电流的二倍频率处。图10b给出了采用传统PI控制的变流器的a、b相并网电流波形以及a相电流频谱,由图可知,传统PI控制的系统的交流并网电流波形为近似正弦波形,二者相差120°,但是由于PI控制不具备抵抗直流电压周期波动影响的能力,造成并网电流中包含150 Hz、250 Hz等低次谐波,这也是与前述理论分析结果相一致的,并网电流THD达到6.56%,严重恶化了并网电流波形质量。
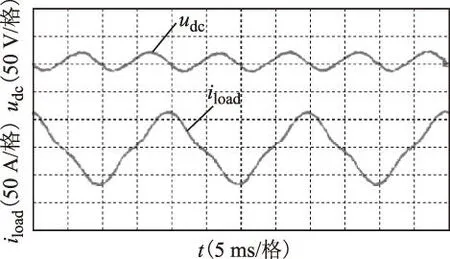
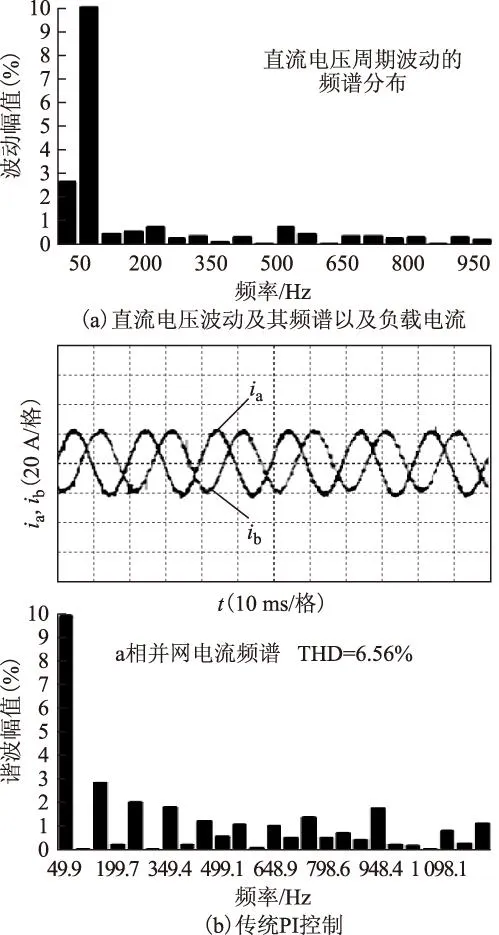
图10 传统PI控制下DC-AC变流器实验波形Fig.10 Experimental waveforms of DC-AC inverter under traditional PI control
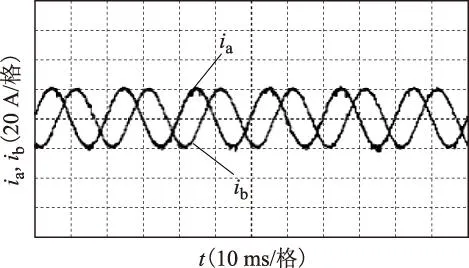
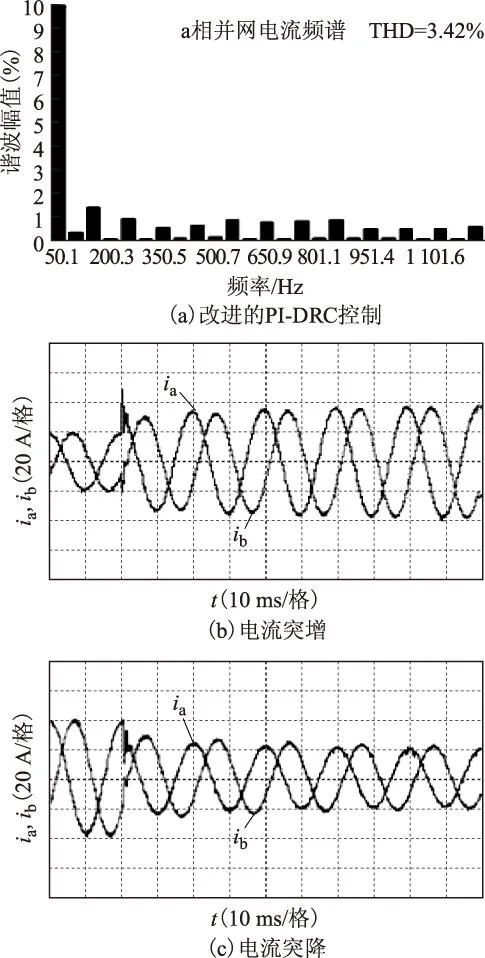
图11 改进后DC-AC变流器实验波形及动态响应Fig.11 Improved and step response experimental waveforms of DC-AC inverter
图11a给出了采用改进后的PI-DRC控制的变流器的a、b相并网电流波形以及a相电流频谱。由图可知,在加入改进的RC后,并网电流保持正弦波形,二者相差120°,并网电流中的150 Hz、250 Hz等低次谐波的幅值显著降低,并网电流THD下降到3.42%,已经满足了相应的并网标准,说明所提出的改进方案很好地抑制了直流电压周期波动对并网电流波形质量的影响。最后,对所提出的控制策略的动态性能进行了实验验证,图11b和图11c给出了a、b相并网电流给定突增和突降的实际电流实验波形,可知在电流给定突变时,经过三个电网周期的过渡过程,实际并网电流跟随上电流给定,具有较快的动态响应性能,同时在动态变化过程中,并网电流并没有出现电流波形明显畸变的情况,说明系统具有较好的稳定性和较宽的功率适应性。
5结论
本文对用于微网交直流母线互联的DC-AC变流器在交直流双侧电压均存在谐波时的性能及其改进控制方案进行了深入研究。当并网电流dq轴分量采用PI控制时,直流电压谐波在交流并网电流中会产生2ωd±ω次谐波,而交流电网电压谐波会产生与自身相同次数的并网电流谐波。引入比例-积分-双重复控制策略用于并网电流dq轴分量的控制,有效地抑制了交直流双侧电压谐波的影响,显著改善了并网电流波形质量。通过线性插值对反馈信号进行估计的重复控制的改进方案有效增强了重复控制器对电网频率变化的适应能力,进一步提高了电网频率变化下的系统谐波抑制能力。
参考文献
[1]陆晓楠,孙凯,Josep Guerrero,等.适用于交直流混合微电网的直流分层控制系统[J].电工技术学报,2013,28(4):35-42.
Lu Xiaonan,Sun Kai,Josep Guerrero,et al.DC hierarchical control system for microgrid applications[J].Transactions of China Electrotechical Society,2013,28(4):35-42.
[2]吴卫民,何远彬,耿攀,等.直流微网研究中的关键技术[J].电工技术学报,2012,27(1):98-106.
Wu Weimin,He Yuanbin,Geng Pan,et al.Key technologies for DC micro-grids[J].Transactions of China Electrotechical Society,2012,27(1):98-106.
[3]Chen D,Xu L.Autonomous DC voltage control of a DC microgrid with multiple slack terminals[J].IEEE Transactions on Power System,2012,27(4):1897-1905.
[4]李春华,朱新坚.基于混合储能的光伏微网动态建模与仿真[J].电网技术,2013,37(1):39-46.
Li Chunhua,Zhu Xinjian.Dynamic modeling and simulation of hybrid energy storage-based photovoltaic microgrid[J].Power System Technology,2013,37(1):39-46.
[5]王晶,李瑞环,束洪春.基于智能多代理的能量协调控制在直流微网中的应用[J].电力自动化设备,2013,33(7):132-138.
Wang Jing,Li Ruihuan,Shu Hongchun.Energy coordination control based on intelligent MAS for DC microgrid[J].Electric Power Automation Equipment,2013,33(7):132-138.
[6]Kakigano H,Miura Y,Ise T.Distribution voltage control for DC microgrids using fuzzy control and gain-scheduling technique[J].IEEE Transactions Power Electronics,2013,28(5):2246-2258.
[7]张新昌.微电网运行控制解决方案及应用[J].电力系统保护与控制,2014,42(10):141-146.
Zhang Xinchang.Solution and application of micro-grid operation control[J].Power System Protection and Control,2014,42(10):141-146.
[8]张犁,孙凯,吴田进,等.基于光伏发电的直流微电网能量变换与管理[J].电工技术学报,2013,28(2):248-254.
Zhang Li,Sun Kai,Wu Tianjin,et al.Energy conversion and management for DC microgrid based on photovoltaic generation[J].Transactions of China Electrotechical Society,2013,28(2):248-254.
[9]丁明,田龙刚,潘浩,等.交直流混合微点网运行控制策略研究[J].电力系统保护与控制,2015,43(9):1-8.
Ding Ming,Tian Longgang,Pan Hao,et al.Research on control strategy of hybrid AC/DC microgrid[J].Power System Protection and Control,2015,43(9):1-8.
[10]肖湘宁.新一代电网中多源多变换复杂交直流系统的基础问题[J].电工技术学报,2015,30(15):1-14.
Xiao Xiangning.Basic problems of the new complex AC-DC power grid with multiple energy resources and multiple conversions[J].Transactions of China Electrotechical Society,2015,30(15):1-14.
[11]高尚,祁新春,谢涛,等.共直流母线光伏-混合储能发电系统及其双重滤波优化控制[J].电力系统保护与控制,2014,42(20):92-97.
Gao Shang,Qi Xinchun,Xie Tao,et al.Common DC bus based PV-hybrid energy storage power system and optimal control using double filters[J].Power System Protection and Control,2014,42(20):92-97.
[12]唐磊,曾成碧,苗虹,等.交直流混合微电网中 AC/DC 双向功率变流器的新控制策略[J].电力系统保护与控制,2013,41(14):13-18.
Tang Lei,Zeng Chengbi,Miao Hong,et al.One novel control strategy of the AC/DC bi-directional power converter in micro-grid[J].Power System Protection and Control,2013,41(14):13-18.
[13]徐友,郑建勇,梅军,等.空间相位解析的三相并网逆变器不平衡控制策略[J].电工技术学报,2013,28(4):133-139.
Xu You,Zheng Jianyong,Mei Jun,et al.A novel control strategy for three-phase grid-connected inverter based on space phase analysis under unbalanced input voltage condition[J].Transactions of China Electrotechical Society,2013,28(4):133-139.
[14]Reyes M,Rodriguez P,Vazquez S,et al.Enhanced decoupled double synchronous reference frame current controller for unbalanced grid-voltage conditions[J].IEEE Transactions on Power Electronics,2012,27(9):3934-3943.
[15]耿强,夏长亮,阎彦,等.电网电压不平衡情况下PWM整流器恒频直接功率控制[J].中国电机工程学报,2010,30(36):79-85.
Geng Qiang,Xia Changliang,Yan Yan,et al.Direct power control in constant switching frequency for PWM rectifier under unbalanced grid voltage conditions[J].Proceedings of the CSEE,2010,30(36):79-85.
[16]Shen Guoqiao,Zhu Xuancai,Zhang Jun,et al.A new feedback method for PR current control of LCL-filter-based grid-connected inverter[J].IEEE Transactions on Industry Electronics,2010,57(6):2033-2041.
[17]全宇,年珩.不平衡及谐波电网下并网逆变器的谐振滑模控制技术[J].中国电机工程学报,2014,34(9):1345-1352.
Quan Yu,Nian Heng.Resonance-based sliding mode control of grid connected inverters under unbalanced and harmonic grid voltages[J].Proceedings of the CSEE,2014,34(9):1345-1352.
[18]张兴,汪杨俊,余畅舟,等.采用PI+重复控制的并网逆变器控制耦合机理及其抑制策略[J].中国电机工程学报,2014,34(30):5287-5295.
Zhang Xing,Wang Yangjun,Yu Changzhou,et al.Mechanism of the control coupling and suppression strategy using PI and repetitive control in grid-connected inverters[J].Proceedings of the CSEE,2014,34(30):5287-5295.
[19]Jiang Shuai,Cao Dong,Li Yuan,et al.Low-THD,fast-transient,and cost-effective synchronous frame repetitive controller for three-phase UPS inverters[J].IEEE Transactions on Power Electronics,2012,27(6):2994-3005.
[20]腾国飞,肖国春,张志波,等.采用重复控制的LCL型并网逆变器单闭环电流控制[J].中国电机工程学报,2013,33(24):13-21.
Teng Guofei,Xiao Guochun,Hang Zhibo,et al.A single-loop current control method for LCL-filtered grid-connected inverters based on the repetitive controller[J].Proceedings of the CSEE,2013,33(24):13-21.
[21]张继元,舒杰,黄磊,等.微网双向变流器的改进型重复控制技术研究[J].电力电子技术,2015,49(1):79-81.
Zhang Jiyuan,Shu Jie,Huang Lei,et al.Research on improved repetitive control applied on microgrid bidirectional converter[J].Power Electronics,2015,49(1):79-81.
[22]赵强松,叶永强,徐国峰,等.改进重复控制在低采样频率逆变器中的应用[J].电工技术学报,2015,30(19):120-127.
Zhao Qiangsong,Ye Yongqiang,Xu Guofeng,et al.Application of improved repetitive control scheme to inverter with low sampling frequency[J].Transactions of China Electrotechical Society,2015,30(19):120-127.
[23]陈东,张军明,钱照明.一种具有频率变化适应性的并网逆变器改进型重复控制方法[J].电工技术学报,2014,29(6):64-70.
Chen Dong,Zhang Junming,Qian Zhaoming.An improved repetitive control scheme for grid-connected inverter with frequency-varying adaptability[J].Transactions of China Electrotechical Society,2014,29(6):64-70.
杨刚男,1986年生,博士研究生,研究方向为微电网控制及保护技术、电力电子技术在电力系统中的应用。
E-mail:yang_g86@126.com(通信作者)
张涛男,1971年生,教授级高工,研究方向为电力系统继电保护、微网新能源接入及控制、柔性直流输电等。
E-mail:zhangtao@sf-auto.com
Improvement Control of Dual-Direction DC-AC Converters for Microgrids
YangGang1YangQixun1ZhangTao2LiuShu2ZhangHeng3
(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power UniversityBeijing102206China 2.Beijing Sifang Automation Co.LtdBeijing100084China 3.State Power Economic Research InstituteBeijing102209China)
AbstractIn the dual-direction DC-AC converter used to connect the DC microgrid and the AC grid, the AC voltage and DC voltage harmonics will generate lower-order harmonics in the AC grid current of the DC-AC converters. In order to tackle the problem, the grid current expression of the DC-AC converter considering the AC and DC dual side voltage harmonics is deduced for the first time and the essence and character of this effect have been revealed. The proportional-integral-dual repetitive control strategy is introduced into the d and q axis of the grid current to control the grid current of the DC-AC converter. Furthermore, aiming at the problem that the non-integral ratio of the sampling and fundamental frequencies in the digital system will decay the gain of the repetitive controller, a gain enhancement approach for the repetitive controller with the desirable sampling point linear interpolation algorithm is proposed to improve the performance of the repetitive control in terms of cancelling the grid voltage harmonics. Detailed simulation and experimental results validate the accuracy and validity of the theoretical analysis and the improvement scheme of the AC grid current waveform quality of the DC-AC converter.
Keywords:Microgrid, DC-AC converter, dual-side voltage harmonics, repetitive control
作者简介
中图分类号:TM46
收稿日期2015-11-30改稿日期2015-12-08
国家高技术研究发展计划(863计划)资助项目(2012AA050208)。

