一种基于HSFC的云资源定位算法

杜晓锋,陈世平

(1.上海理工大学 光电信息与计算机工程学院,上海　200093;2.上海理工大学 信息化办公室,上海　200093)



一种基于HSFC的云资源定位算法

杜晓锋1,陈世平2

(1.上海理工大学 光电信息与计算机工程学院,上海200093;2.上海理工大学 信息化办公室,上海200093)

摘要针对云计算环境下,云资源的模糊查询问题,提出了一种云资源定位算法。该算法建立在双层Chord环模型上,同时结合Hilbert空间填充曲线(HSFC),实现多维属性的降维,进而完成云资源的定位。另外,该算法将整个资源空间划分成多个资源区间,并提出邻居区间的概念,通过邻居区间,可较好地实现云资源的模糊查询,此外该算法还为每个属性设置属性权值,以此减少网络请求数量。实验表明,该算法不但能有效解决云资源的模糊查询,且能降低查询时延,提高查询效率。

关键词云计算;资源定位;Hilbert空间填充曲线

云计算是一种以互联网为基础,以服务的方式动态易扩展地提供虚拟化资源的计算方式。与传统的计算模型不同,其无需用户亲自管理资源,而是以服务的方式直接提供给用户。因此,对于云资源的快速定位就成了云计算的关键技术之一。所谓云资源定位就是根据用户提出的资源属性类型和值的组合,快速找到满足要求的资源,这是一种多属性区间查找方式。

为实现快速有效的云资源定位,需要改变传统的网络结构模式,目前,将云计算和对等网络技术相结合构成云对等网络是一种比较常见的方法。云对等网络由常年稳定在线的云服务器构成。因此,每个节点都具有较强的处理能力,较大的存储空间,极好的稳定性。进而,在研究对云资源的快速定位时,节点的处理能力,存储空间以及节点失效等问题已无需过多考虑。

1相关研究

传统的P2P资源定位系统实现多属性区间查找的方法大致有3类:

(1)采用特定的网络拓扑结构,比如文献[1～2]中的MAMSO和文献[3]中的MAHO,其均设计了复杂的网络拓扑结构,这些结构自身能够支持多属性查找。然而,其结构过于复杂,维护开销过高,也不具备良好的可扩展性;

(2)采用多层网络模型,比如文献[4～8],这些系统都采用分层的P2P网络结构,逐层进行单一属性查找,将多属性查找拆分成多个单属性查找。最终,将多个查询结果集做交集运算。这种查询方式会带来较大的网络负载和查询延时;

(3)应用空间填充曲线将多维属性映射到一维索引空间,然后再结合与之相适应的P2P网络结构,以此来实现多属性查找,比如文献[9]中的Squid和文献[10]的OID,以及文献[11]。

针对以上研究,该文提出了一种基于Hilbert空间填充曲线的云资源定位对等网络系统,该系统采用双层Chord网络,结合Hilbert曲线,同时结合邻居资源等机制,着力研究多属性模糊查询问题。

2系统设计

2.1相关定义

下面给出系统中将会用到的一些术语的形式化定义:

定义1资源对象。具有个属性的云资源对象用数据向量集合D={(A1,V1),(A2,V2),…,(Ai,Vi),…,(An,Vn)}表示,其中Ai表示描述资源某一特征的属性,Vi是对应属性Ai的属性值。

定义2资源编码表。将属性类型组合相同的资源聚集在一起,形成资源簇,再将资源簇内的每个维度属性的值都用m元组的编码进行划分,从而形成一张多维资源编码表。

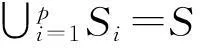
2.2系统拓扑结构

该系统采用双层Chord模型。第一层为超环层,实现资源类型信息的索引。超环上每一个超级节点对应一种资源类型组合,根据资源类型组合匹配到对应的超级节点,进入对应的子环层,由于子环层是具有同一种资源类型组合的资源簇,资源簇的规模相对于整个对等网络是较小的,所以查询效率较高,如图1所示。

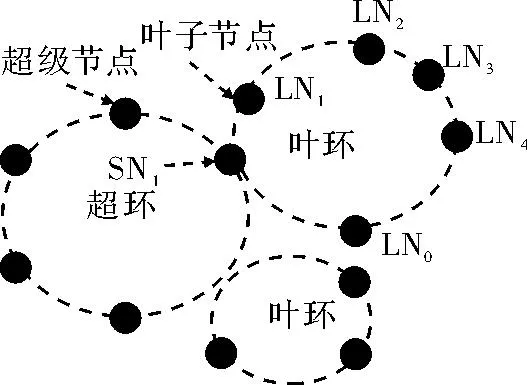
图1　系统网络拓扑图

然而,当资源类型种类较多时,所产生的资源类型组合也就越多,可达到2n-1,其中n是资源种类个数,为避免超环过于庞大,该文采用属性域子集的方式。如定义3所示,关键在于p的取值,当p取较小,而n较大时,p≪2n,就能大幅缩小超环的规模,即减少资源簇子环的数量,提高了查询效率。

由于每个属性组合被查询的概率是不一样的,可参考文献[12],因此令查询全集QS={q1,q2,…,qp-1,qp,…,qk},其中qi表示对某一子查询,k表示查询总数。对于1≤p≤k,有P(q1)≥P(qp)≥P(qk),该文将前p-1个查询对应的属性域子集单建索引,每一个属性域子集对应超环层的一个超节点,而其他k-p+1查询子集对应的属性域子集合并成一个属性域子集,只对应超环的一个超级节点,因此超环上只会有p个节点,超环规模得到大幅减小。

2.3HSFC编码

为提高资源检索效率,该文将每个维度的属性值均分成若干段,形成一个多维资源空间,然后利用空间填充曲线将多维资源降维,使之映射到单维资源环上,而Hilbert[13]曲线具有最好数据聚集特性,故该文采用了Hilbert空间填充曲线(Hilbert Space-Filling Curve,HSFC)编码。

将一个d维空间看作一个d维的立方体,并将其切分为nd个相同的子立方体,n是属性的维度,Hilbert曲线就是一条依次连接两个相邻子立方体中心点的折线,空间中每个子立方体都被折线穿过一次,且只穿过一次。如图2(a)所示,为一个2维空间的Hilbert曲线,其中n=2,d=2;同时,可将其进行l次翻转变化得到nl×d个子空间Hilbert曲线,如图2(b)所示,是由图2(a)经过两次翻转变化得到的,其中n=2,d=2,l=2。

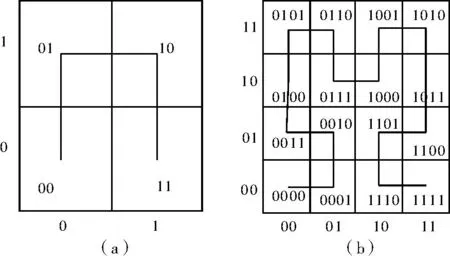
图2　Hilbert填充曲线图

每个资源簇就是一个资源空间,资源簇内每种属性就是资源空间的一个维度,n维属性就形成一个n维空间。每个维度的属性再被划分为r个区间,这样便形成了rn个多维区间。每个资源簇保存一张资源编码表。比如一个资源簇上的资源有两个属性:内存和带宽。其属性值被划分成4个区间,用2 bit来编码,比如,内存有1 GB,2 GB,3 GB,4 GB,编码为00,10,10,11,带宽有100 Mbit·s-1,200 Mbit·s-1,300 Mbit·s-1,400 Mbit·s-1,编码为00,01,10,11。对于内存=2 GB,带宽=200 Mbit·s-1的资源,若用表示内存=2 GB,用(01)2表示带宽=200 Mbit·s-1,则资源R属性值的键值用(0101)2表示。如图3所示,其中黑色阴影部分就表示资源R。

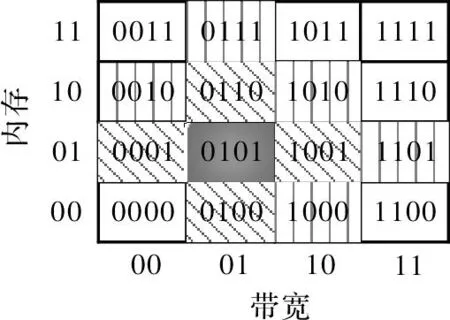
图3　二维属性资源编码图

资源编码表中的资源编码可以和HSFC码相互转化。如图2(b)的横轴表示带宽,纵轴表示内存,图3所示的资源编码表与之对应,则图3中的资源R(0101)2可转化为相应的HSFC编码(0010)HSFC,图2(b)中的曲线是将图3中的资源编码表转化为HSFC值所形成的一维Hilbert曲线,实现了降维的目的。然后再将Hilbert曲线首尾相连,应用到Chord环上。节点的加入和离开还是依照Chord的规则,而资源的检索则结合了HSFC码和Chord的相关规则。

2.4邻居区间

一个维的资源簇空间会被划分个多维区间。除了在空间边界上的多维区间,其他的多维区间在任意维度上都有两个相邻的区间,这些区间便是邻居区间。如图3所示,黑色阴影表示的资源区间(0101)2拥有4个邻居区间,即斜阴影表示的(0001)2,(0100)2,(1001)2,(0110)2。将邻居区间的资源称为邻居资源,将每个资源区间的资源和其邻居资源部署在该资源区间对应的节点上,这样当系统检索到某一个节点时,不但能获得该节点对应的资源区间的资源,还能获得其邻居资源,这对于模糊查询是有较大帮助的,而系统中的节点均是性能极强的云服务器,所以暂时无需考虑多部署资源对于节点性能的影响。邻居区间对应的节点称为邻居节点,当然,邻居节点也会有其自身的邻居节点。每个节点都保存了邻居节点的信息,方便在本节点找不到符合要求的资源时,查找邻居节点。

3资源查找

由于用户请求的资源往往要比实际能够满足用户需求所需的最低资源要求更高,所以系统在找不到完全满足请求的资源时,提供比请求要求稍低的资源也能满足用户需求。因此,该文为属性设置一个权重W,取值为0或1。0表示请求中该属性的值为最低要求,假如提供比该值更小的资源,将不能满足用户的需求。1则相反,表示即使提供比要求的属性值稍小的资源,也能满足需求。这能进一步减少网络请求数,加快查询速度。

3.1查询算法

(1)节点N接收到查询请求Q,若N是叶节点,则N将请求提交到超环,然后在超环上匹配请求Q中的属性类型组合,找到相应的超级节点,若节点N是超级节点,则直接在超环上查找与请求Q属性类型组合对应的超级节点。若在超环上未找到与请求Q属性类型组合对应的超级节点,则返回查询失败。否则进行步骤(2);

(2)若在超环上找到了与请求Q中属性类型组合相适应的超级节点,则进入与该超级节点相连的叶环中进行进一步查询。首先根据请求Q的属性值信息查询属性资源编码表,确定属性资源区间编码,再将其转化成HSFC编码,然后根据Chord算法定位到提供该资源的节点,若在节点上找到了满足请求Q的资源,则将节点的IP提供给用户,让节点和用户直接通信,获取资源。由于该文是将某一个资源区间及其邻居资源部署在同一个节点上,所以这里查找一个节点不但能查找与该节点本身对应的资源区间,还能查询其邻居资源,这就增加了在该节点查询成功的机率。若在该节点找不到适合的资源,即与该节点本身对应的资源区间的资源不足,且其邻居资源也不足,则转入步骤(3);

(3)当在某个节点没有找到请求的资源时,节点根据请求中每个属性的权值,选择有可能拥有满足请求资源的邻居节点转发请求,比如某个属性权值为0,则只需向在这一属性维度上值增长方向的邻居节点转发请求,而在这个属性维度上值降低方向上的邻居节点可忽略,由此便减少了网络请求,加快了查询速度。然后重复步骤(2)。此时,由于每个邻居区间都有自己的邻居区间,所以查询到的资源区间进一步增多,查询成功的几率进一步增大。若进一步重复步骤(3),能查询到的资源区间会越来越多,但没有必要。因此,该文最多只重复两次步骤(3)。如果进行了两次步骤(3)之后还没有找到满足请求的资源,则返回失败。

假设图1中节点接收到一个请求,其中内存为2 GB,带宽为200 Mbit·s-1,两者的权值都为0,LN0首先将请求通过SN1提交到超环,匹配到超级节点SN1是内存和带宽这两个属性组合对应的超级节点,则进入SN1超级节点所在的叶环,首先查找图3所示的资源编码表,发现内存为2 GB,带宽为200 Mbit·s-1对应的资源区间是(0101)2,接着转化成HSFC编码,为图2(b)中(0010)HSFC,然后根据Chord算法找到对应的叶节点,假设是LN2,此时已经查找了资源区间(0001)2,(0100)2,(1001)2,(0110)2,(0110)2,发现节点上没有满足的资源,则查找邻居节点,由于两个属性的权值均为0,只需要查找资源编码表中(0110)2,(1001)2对应的节点,LN2将请求(0110)2,(1001)2对应的节点,这就能够查找到资源区间(0010)2,(0111)2,(1010)2,(1101)2,(1000)2,即图3中竖线阴影表示的资源区间,最后在其中找到了满足要求的资源,将节点IP提交给用户,否则将请求转发给(0110)2和(1001)2对应的邻居节点。

3.2性能分析

由于整个网络均是按照Chord组织的,所以不过多分析系统的查找复杂度,该文着重分析将某个资源区间及其邻居资源部署在同一个节点上,以及属性权值对于资源查找的影响。

定义查找范围比μ为某一节点发出一次请求后总共所查询到的资源编码表中资源区间的数量和资源编码表中总的资源区间数量的比值。在发出请求数量相同的情况下,能查询到的资源区间数越多,则在该步请求时查询成功的可能性越大,即查询速度越快,所以该文使用μ来分析资源查询的性能。

假设属性维度为n,每个属性维度的值区间个数为r,当不将邻居资源部署在同一个节点上时,假设某一个资源区间有2n个邻居区间,则该资源区间对应的节点发出第一次请求有

当将邻居资源部署在同一个节点上时,且某个资源区间及其邻居区间都有2n个邻居区间,则该资源区间对应的节点发出第一次请求有

该资源区间对应的节点发出第二步请求有

由此可见,将邻居资源部署在同一个节点上,只是稍微增加了一点云服务器的负担,但却使得在相同的网络请求数下,能够查找到的资源区间数量乘n倍增长,资源查找的速度和成功率都得到提升。

另外,假设n维属性中有w个属性加上了属性权值,则在第一个节点查找失败时,该节点所需要发出的网络请求数是

L=w+2(n-w)=2n-w

当n=w,即所有属性都加上了权值,则最多能将网络请求数减少一半。

将邻居资源部署在同一个节点上使得在相同网络请求数下,资源查找性能得以优化,又通过属性权值使网络请求数减少,在两种因素的作用下,资源查找性能得到较大优化。

4实验

实验环境为CPU3.40GHz,内存2GB,Linux操作系统,JDK1.6,在1.0.5版本的PeerSim上用Java实现的一个模拟环境。

实验1对比将邻居资源部署在同一节点上前后网络平均查询时延,以验证将邻居资源部署在同一节点上对于系统性能的优化。属性维度为4,并且不为属性加上权值,网络节点数为1 000个,1 500个,2 000个,2 500个,3 000个和3 500个,网络超节点都为10个,每个属性维度分8个属性值区间。如图4所示,折线1表示将邻居资源部署在同一节点之前,折线2表示将邻居资源部署在同一节点之后,可以看出,将邻居资源部署在同一节点上可加快资源查找速度。

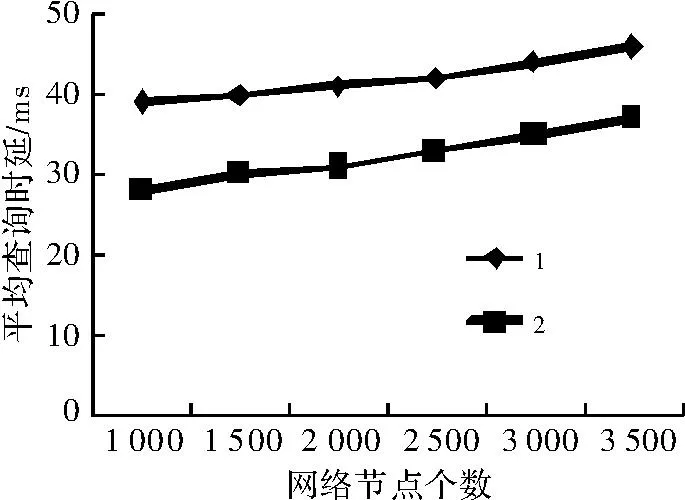
图4　将邻居资源部署在同一节点前后查询时延变化

实验2验证属性权值对于减少查找时延的影响。网络节点数为3 000个,属性种类个数为1个到10个,每个属性权值的个数为0～5个。同时,将邻居资源部署在同一个节点上,每组实验做10次,取平均值,得到结果如图5所示。因一个属性只加一个权值,所以权值个数大于属性维度的情况是不存在的,在图5中用虚线表示。由图5可看出,平均查询延时随着属性维度的增加快速增长。同时可看出,在属性维度相同的情况下,属性权值个数越多,平均查询时延越小,而且当属性维度和权值个数相同时,降低查询时延的效果最佳。

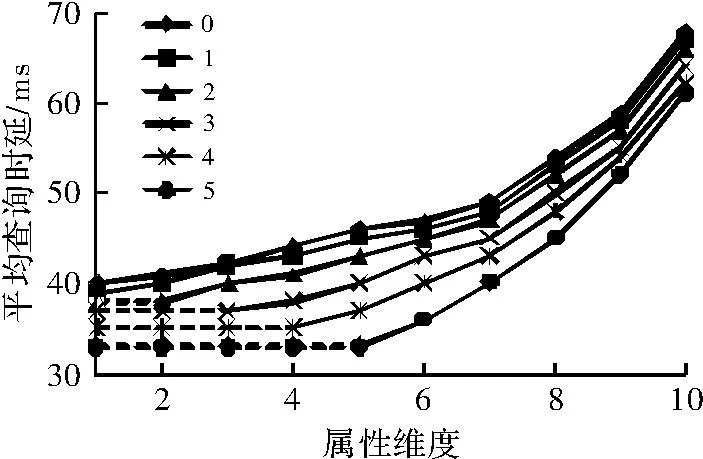
图5　属性权值与查询时延关系图

5结束语

该文提出了一种基于HSFC的资源定位系统,主要是将资源区间及邻居区间的资源部署在一个节点上以提高在相同请求步数下资源查找效率,同时为属性加上权值,以减少网络请求,从而提高资源查找效率。但该文的属性权值过于简单,只有0和1两种,可通过细化属性权值的设置来加强属性重要性的区分度。同时,该文是将某个资源区间在每个维度上相邻的资源区间定义为邻居资源区间,可以进一步探讨邻居资源区间的定义,使得部署在同一节点上的邻居资源更加合理有效。

参考文献

[1]Bharambe A R,Agrawal M,Seshan S.Mercury:supporting scalable multi-attribute range queries[C].Portland,OR:ACM/SIGCOMM 2004 Conference on Computer Communications,2004.

[2]YoufuY U,LAI Huanchou.A semi-strucured overlay for multi-attribute range queries in cloud computing[C].Hong Kong,China:IEEE 13th International Conference on Computational Science and Engineering (CSE 2010),2010.

[3]LAI Kuanchou,YU Youfu.A scalable multi-attribute hybrid overlay for range queries on the cloud.[J].Information System Fontier,2012(14):895-908.

[4]Papadakis H,Trunfio P,Talia D,et al.Design and implementation of a hybrid p2p-based grid resource discovery system[C].Heraklion,Greece:Joint Workshop on Making Grids Works,2007.

[5]Yang Min,Yang Yuanyuan.An efficient hybrid peer-to-peer system for distributed data sharing[J].IEEE Transactions on Computers,2010,59(9):1158-1171.

[6]李钊伟,陈世平.支持多维查找的资源共享设计[J].计算机应用研究,2013,30(7):2056-2059,2084.

[7]张明英,胡德敏,高丽萍,等.基于结构化对等网络的云资源查询算法[J].计算机应用研究,2015,32(2):532-535.

[8]余星,胡德敏.基于P2P网络的云资源多维查询算法[J].计算机应用研究,2014,31(10):3061-3064.

[9]Schmidt C,Parashar M.Flexible information discovery in decentralized distributed systems[C].Seattle,WA:12th IEEE International Symposium on High-Performance Distributed Computing,2003.

[10]Memon F,Tiebler D,Tomsu M,et al.OID:Optimized information discovery using space filling curves in P2P overlay networks[C].Melbourne,Australia:14th International Conference on Parallel and Distributed Systems,2008.

[11]Lawder J K,King Pjh.Using space-filling curves for multi-dimensional indexing[C].Exter,England:17th British National Conference on Databases (BNCOD 17),2000.

[12]Klemn A,Lindemann C,Vernon K,et al.Characterizing the query behavior in peer-to-peer file sharing systems[C].New York:the 4th ACM SIGCOMM Conference on Internet Measurement,2004.

[13]Moon B,Jagadish H V,Faloutsos C,et al.Analysis of theclustering properties of the hilbert space-filling curve[J].IEEE Transactions on Knowledge and Data Engineering,2001,13(1):124-141.

An HSFC-based Cloud Source Discovery Algorithm

DU Xiaofeng1,CHEN Shiping2

(1.School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;2.Information Office,University of Shanghai for Science and Technology,Shanghai 200093,China)

AbstractA cloud resource discovery algorithm is proposed for the fuzzy query of cloud resource in cloud computing.Based on a hierarchical Chord model and combined with Hilbert Space Filling Curve (HSFC),this algorithm realizes dimensionality reduction of multidimensional attributes and then completes cloud source discovery.In addition,the source space is divided into several multidimensional intervals,and the concept of neighbor interval is put forward,with which the fuzzy query of cloud resource is resolved.Every attribute is given a weight to reduce requests in the network.The experimental results show that the algorithm not only resolves the fuzzy query of cloud resource,but also reduces delay as much as possible to improve query efficiency.

Keywordscloud computing;source discovery;HSFC

中图分类号TP391

文献标识码A

文章编号1007-7820(2016)04-032-05

doi:10.16180/j.cnki.issn1007-7820.2016.04.009

作者简介:杜晓锋(1990—),男,硕士研究生。研究方向:计算机网络。陈世平(1964—),男,教授,博士生导师。研究研究方向:计算机网络。

基金项目:国家自然科学基金资助项目(61170277;61472256);上海市教委科研创新重点基金资助项目(12zz137);上海市一流学科建设基金资助项目(S1201YLXK)

收稿日期:2015- 09- 11