基于改进的模糊控制PMSM矢量控制系统研究
徐奔奔,周芝峰,霍文明,杨恩星
(1. 上海电机学院电气工程学院,上海200230; 2.上海电气输配电技术中心,上海200042)
基于改进的模糊控制PMSM矢量控制系统研究
徐奔奔1,周芝峰1,霍文明1,杨恩星2
(1. 上海电机学院电气工程学院,上海200230; 2.上海电气输配电技术中心,上海200042)
摘要:为更好地改善永磁同步电机(PMSM)调速性能,在传统PI控制方法与一般模糊PI控制方法的基础上,跟据Clark、Park变换、空间矢量调制(SVPWM)和磁场定向控制等理论,提出了一种改进的模糊PI控制方法并用于双闭环调速系统的速度环中。借助MATLAB/SIMULINK搭建控制系统仿真模型,并对永磁同步电机的重要性能进行对比分析。结果表明,引入改进的模糊PI控制器后,调速系统具有很强的适应性、鲁棒性和抗干扰性,能快速跟踪速度参考值,永磁同步电机输出电磁转矩波动量较小,性能得到改善。
关键词:永磁同步电机;矢量控制;模糊控制;SIMULINK
0引言
现代电力电子学、新型电机控制理论,结合永磁同步电机自身诸多优点,使得永磁同步电机的应用在众多领域受到越来越多的青睐[1,2]。研究表明,由于永磁同步电机系统本身的非线性特点,依据经典控制理论以及各种现代控制理论提出的控制策略都强调精确的电机数学模型,当系统受到外界因素干扰或者自身参数发生变化的时候,系统性能总会受到影响。传统的PI 或 PID 控制方式,虽参数调整方便,也有一定的控制精度,由于它高度依赖于电机数学模型,在控制性能上也存在局限性。智能控制方法与各种优化算法的出现为控制复杂的永磁同步电机系统开辟了一条新的道路[3],其中,模糊控制理论在电机控制中的应用就是成功的范例。模糊控制器不同传统PI控制,它不依赖被控对象的精确数学模型,是易于理解的、不易受影响的、较理想的非线性控制器[4]。模糊控制器本身特性相当于一种系数时变的PD控制器,也存在着一个较大的缺点,就是当电机系统具有负载扰动时,模糊控制难以有效消除稳态误差,使得控制精度不高[5],这主要是由于控制器中缺少积分作用。并且模糊控制器由于其自身的特点(依据专家经验)对信息的简单模糊处理很容易致使控制系统性能变差,难以达到理想的控制精度。因此为了改善永磁同步电机调速系统的稳态性能,通过分析基本模糊控制器的原理,在其传统的方法上作进一步改进,加入一种对误差信号精确量积分的环节。在双闭环调速系统中将改进的模糊控制器用于系统的外环(速度环)中。
1PMSM数学模型及矢量控制原理
1.1PMSM数学模型
永磁同步电机矢量控制原理是建立在等效坐标变换理论基础上的,其在三相坐标系中的数学模型经过Clark、Park变换后可得到在dq坐标系的数学模型,其中电压方程为:
(1)
式中:Rs为定子绕组电阻,ωr为转子角速度,ud,uq,id,iq分别为d轴q轴电压和电流;Rs为定子绕组电阻;Ld,Lq为定子dq轴等效电感;ωr;ψd,ψq为dq轴等效磁链分量。
磁链方程:
(2)
式中:ψf为永磁铁的励磁磁链。
电磁转矩方程:
(3)
式中:Te为电磁转矩;np为极对数。
运动方程:
(4)
式中:TL为负载转矩;J为转动惯量。
1.2矢量控制原理
永磁同步电机矢量控制原理的本质就是对定子电流空间矢量相位和幅值的控制。可以理解为对电磁转矩和磁阻转矩的控制,也就是为对d轴和q轴电流的控制,同一输出电磁转矩有多个dq轴电流的控制组合,其中主要的矢量控制方式有id=0控制、恒转矩控制、弱磁控制等。各种控制方法针对目标不同,控制效果也有所差别
本文采用id=0控制,这种控制方式使电流矢量全部位于q轴,定子电流全部来产生转矩,励磁电流为零。这样,就可以通过单一的控制q轴电流分量来控制电磁转矩,获得了与控制直流电机相同的作用效果,因为id=0,转矩方程可简化为:
(5)
可见,反馈电流经变换后得到id、iq与所设电流参考值比较,再进行调制可以获得电压信号uα和uβ,根据空间矢量调制(SVPWM)与逆变器的配合来合成控制电机所需的电压矢量。其控制方式是通过交替使用几个不同的电压空间矢量来实现对磁链的跟踪。
1.3矢量控制系统框图
永磁同步电机(PMSM)矢量控制系统框图见图1所示。
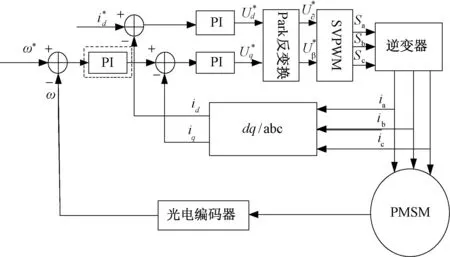
图1 永磁同步电机磁场定向控制框图
由图1可以清晰看到转矩电流iq参考值由电机运行时检测到的电机转速和输入参考转速相减,并将其差值通过外环PI控制器计算得到。同时给定定子电流励磁分量idef,采用id=0的控制策略,激磁电流idef=0。通过电流传感器检测三相电流ia、ib、ic,并进行Clarke、Park变换,将它们转换到dq旋转坐标系中,再将转换后的电流与它们的参考电流idef、iqef分别进行比较,差值再通过PI控制器获得dq坐标系下的电压信号Ud、Uq。Ud、Uq经过Park逆变换得到两相静止坐标系下的电压信号Uα,Uβ,并将其送入SVPWM中产生控制脉冲、控制逆变器,进而去得到控制定子三相对称绕组的实际电流。
2改进的模糊PI控制器设计方案
永磁同步电机采用双闭环矢量调制系统,外环用改进的模糊PI控制器,内环用一般PI控制器。如上图1所示,将改进的模糊PI控制器代替虚线框中的传统PI控制器。
外环决定系统的动态性能,而且扰动因素给被控对象带来的干扰也可由外环加以抑制或弥补,所以改进的模糊PI控制策略施加于矢量控制系统的外环而不是内环。一般模糊控制器也存在许多不足,文献[7]提出模糊自整定PI的永磁同步电机矢量控制系统,相对传统的PI控制,永磁同步电机的性能有明显的优化,但是在启动性、抗干扰性方面,减小稳态误差提高控制精度方面仍存在不足。文献[8],[9]等提出用遗传算法,粒子群算法在线优化模糊PI控制,通过MATLAB/SIMULINK 仿真分析,能在一定程度上优化模糊PI控制,提高永磁伺服控制系统的性能。但是考虑实际过程中DSP等控制芯片的时钟周期、实时性问题,复杂性算法在线优化模糊PI控制难度很大,而且会降低整个控制系统的快速性。因此,在不考虑引用复杂算法优化模糊PI控制器的基础上,提出一种新型模糊-积分混合智能控制替换传统模糊PI控制,使整个控制系统的稳态性能得到提高与优化。改进的模糊PI控制器如下图2所示。一般来讲模糊控制只有偏差与偏差变化率两个输入量,相当于一个变采参数的PD控制器。文献[10]提出一种加入积分环节的模糊控制器,也说明了所提出的方法容易引起极限环震荡。这里在前者的基础上做了改进,引入的积分控制作用是直接对误差的精确量进行积分,再与模糊控制器的输出变量叠加后构成总的输出变量。因为在控制系统中误差是连续变化的,所以积分的控制作用也连续变化,因而可以进一步消除静态误差,增强系统的快速性。下图2是改进的模糊控制器结构图,图3为其仿真模块结构图。
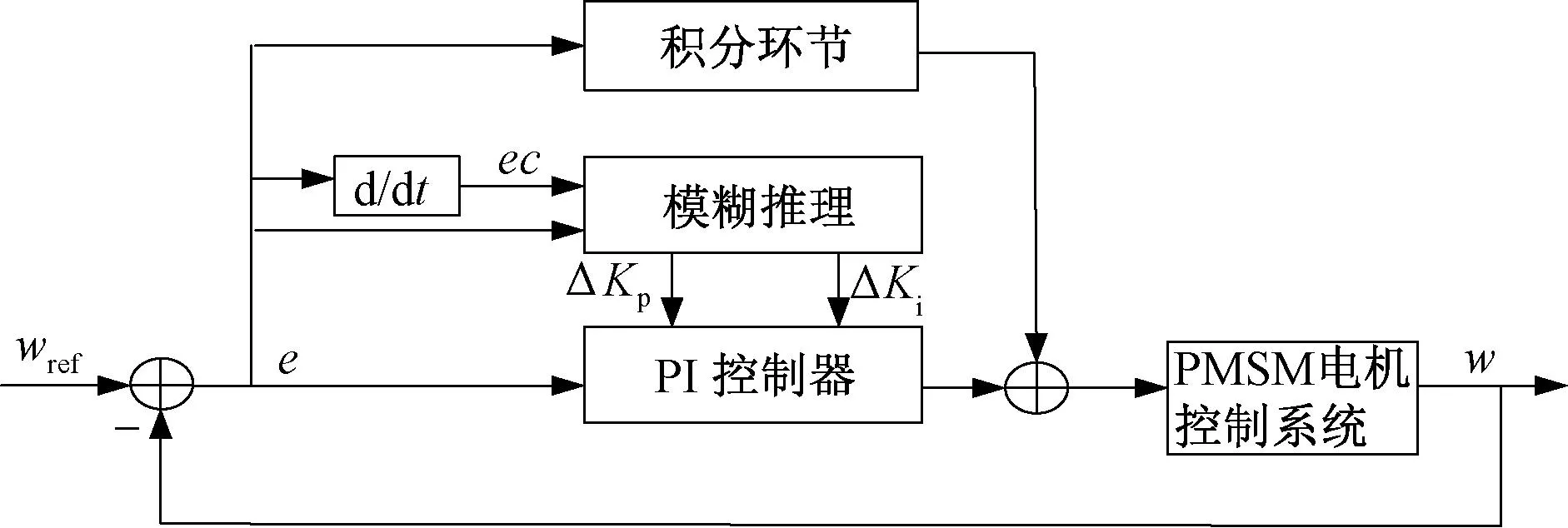
图2 改进的模糊PI控制器结构框图
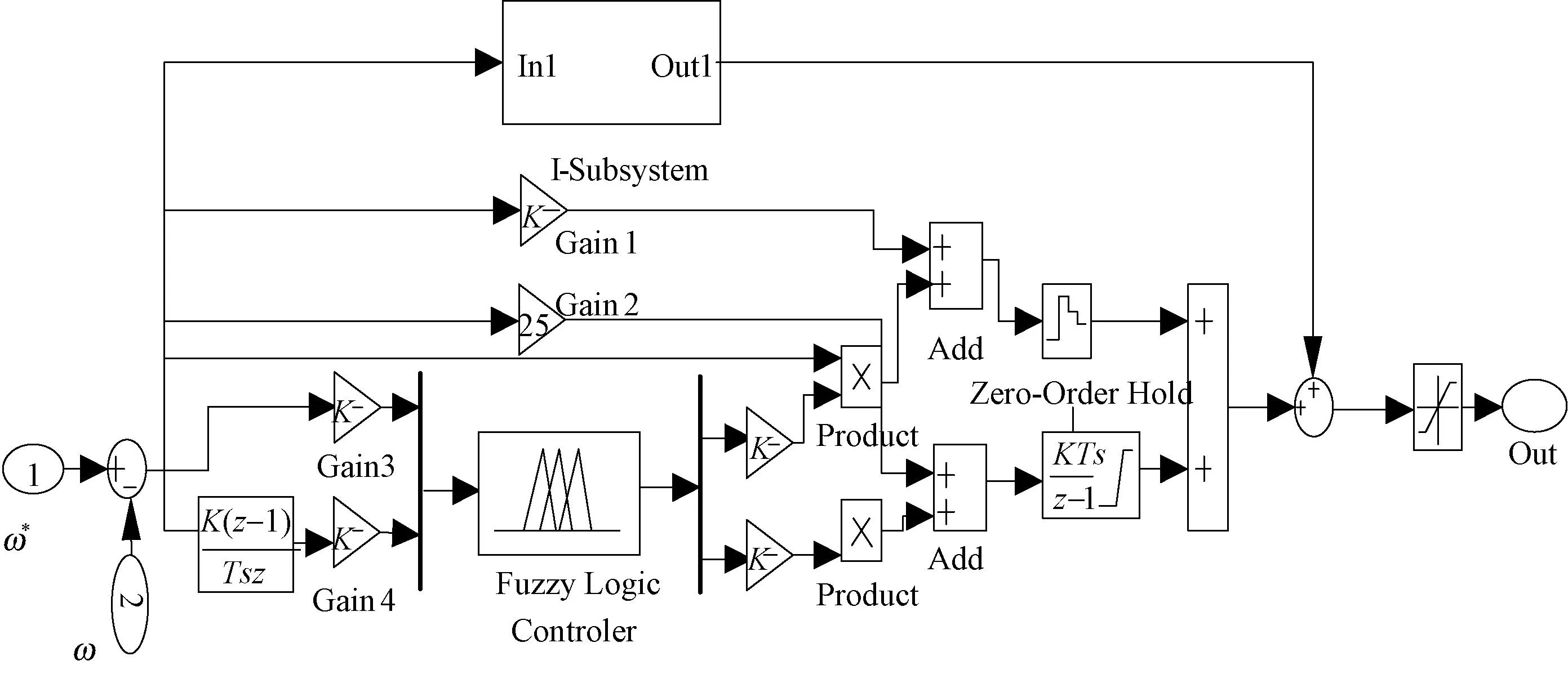
图3 改进的模糊PI控制器仿真结构框图
2.1模糊控制器论域选择
所设计的模糊控制器为两输入两输出结构,输入为参考转速ω*和实际所测转速ω的偏差e及偏差变化率ec,输出为转速环PI参数变化量ΔKp和ΔKi。
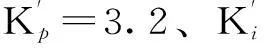
输出端ΔKp和ΔKi的模糊论域为UΔkp={-6,-4,-2,0,2,4,6}、UΔki={-6,-4,-2,0,2,4,6}。模糊控制器输入输出语言变量同取为{负大(NB),负中(NM),负小(NS),零(ZR),正小(PS),正中(PM),正大(PB) }七个模糊子集。
2.2隶属度函数的确定
先对模糊控制器的输入信号进行模糊化再转换到对应的模糊论域进行模糊推理。假设模糊控制器输入信号的实际输入论域为[-i,i],模糊论域为[-n,n],则从实际论域到模糊论域转化的量化因子为K=n/i,当实际论域发生变化时,正确的调节量化因子也可以实现模糊控制。同样,模糊输出量也需要经过清晰化转换到对应的实际论域。假设输出量的实际论域为[-u,u],则从模糊论域转换到实际论域的比例因子为Ku=u/n。
如图4, 一般模糊控制器中输入与输出变量的隶属度函数是根据实际工程中的专家经验来确定。参考众多文献,一般用的比较多的隶属度函数有三角形、正态形等。输入偏差的模糊子集正大(PB)采用Z型隶属度函数,负大(NB)采用S型隶属度函数,其他均为三角形隶属度函数。下图为在MATLAB中设计控制器时输入转速偏差e的隶属度函数。其中偏差e的量化因子Ke=3/45。
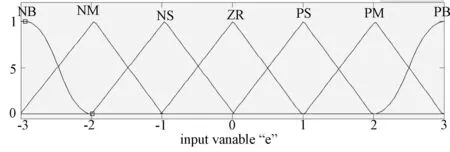
图4 输入e/ec的隶属度函数
同样,转速偏差变化率ec的模糊子集负大(NB)采用Z型隶属函数,正大(PB)采用S型隶属函数,其他均为三角形隶属函数。其隶属度函数同上图。根据转速偏差变化率ec的基本论域和模糊论域,可得偏差变化率ec的量化因子Kec=6/2.25。
类似,输出ΔKp和ΔKi的模糊子集负大(NB)采用Z型隶属度函数,正大(PB)釆用S型隶属度函数,其他均为三角形隶属度函数。根据输出参数的基本论域和模糊论域可得ΔKp的比例因子为Kui=0.64/6,ΔKi的比例因子为Kui=5/6。
2.3模糊规则的确定
总结工程设计人员的技术知识和实际操作经验,推理计算采用 “Mamdani”模糊推理算法。Mamdani型模糊控制器的模糊控制规则编辑器以if...then的形式输入模糊控制规则,共49条。
模糊PI算法公式为:
根据参考文献[6]提出的模糊控制规则并经过适当的修改后得到ΔKp和ΔKi模糊控制规则表,如表(1)ΔKp模糊控制规则表,表(2)ΔKi模糊控制规则表。
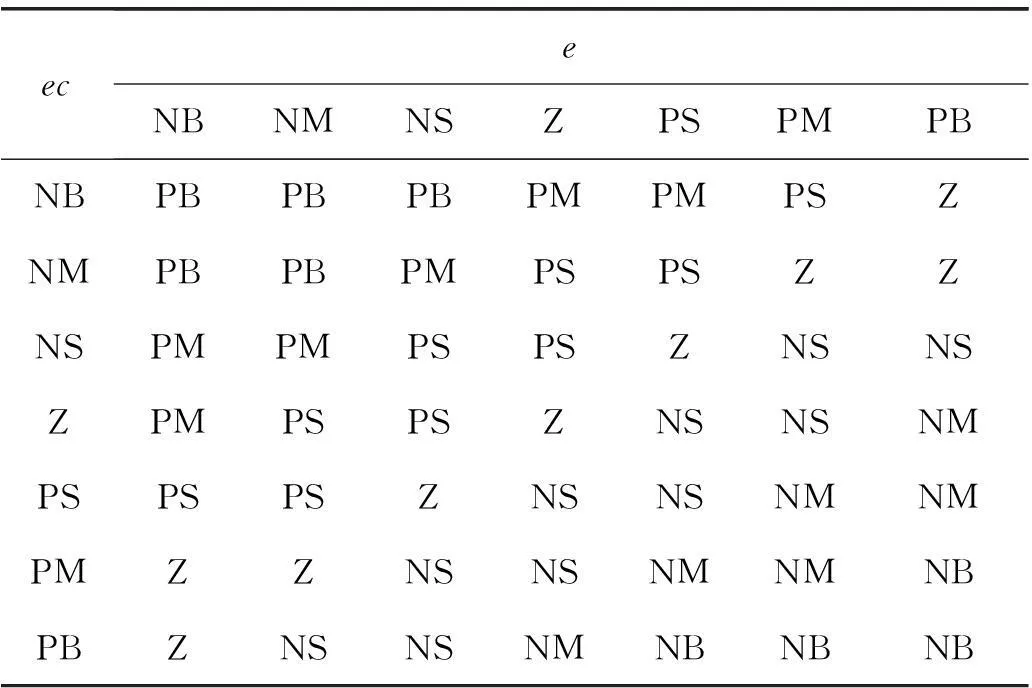
表1 ΔKp模糊控制规则表
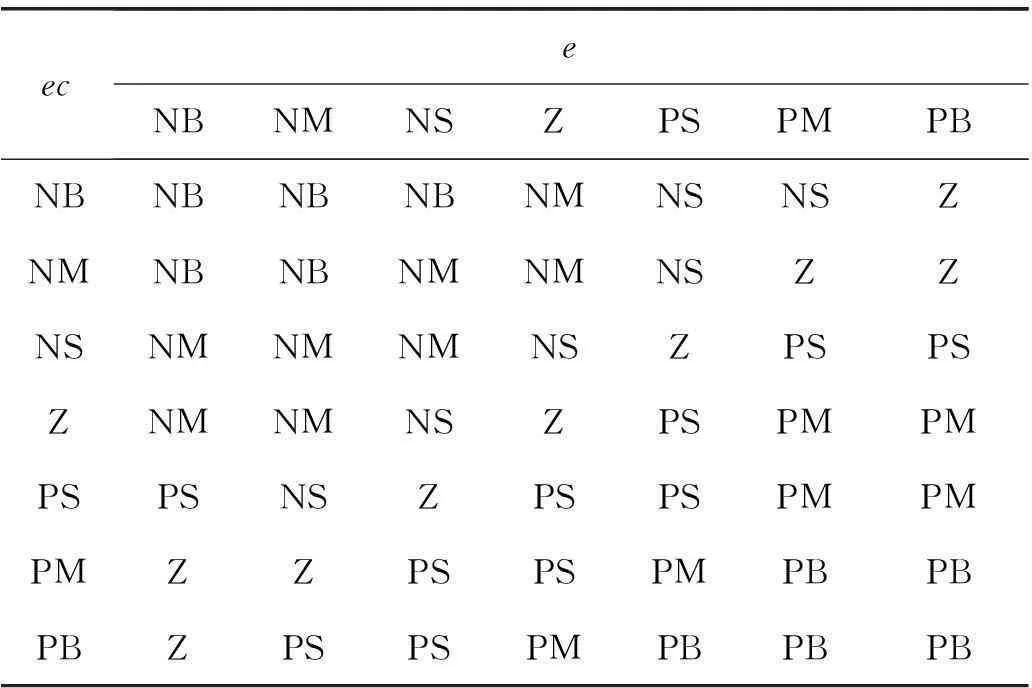
表2 ΔKi模糊控制规则表
2.4解模糊化
给模糊控制器输入的变量为精确量,经过模糊化与模糊推理得到的控制输出量为模糊量,因为模糊量不能直接用于控制对象,必须经过反模糊化转化成精确量才能用于被控对象。用的比较多的解模糊化方法主要有三种,主要包括最大隶属度法、重心法和加权平均法。重心法计算稍微复杂,但却包含了输出模糊子集的所有元素的信息,在计算能力满足的条件下通常选用该方法。本文解模糊化方法采用重心法,该方法的计算公式为:
(6)
式中:U为解模糊后输出的精确量;xi为输出变量的模糊值;U(xi)为对应的隶属度函数值;根据上式可以求得输出ΔKp和ΔKi。
3仿真分析
在MATLAB环境下建立永磁同步电机伺服系统的仿真模型,并对改进模糊PI控制器的模糊控制策略进行仿真试验。设置好电机参数后,设仿真时间为0.2 s。图5中给定初始负载转矩给定为5 N·m,在0.07 s时突加负载转矩为10 N·m。仿真结果如图所示。
当给定参考转速1 500 r/min时,在图5中曲线1为传统PI控制下的转速曲线,曲线2为一般模糊PI控制下的转速曲线,曲线3为改进的模糊PI控制下的转速曲线,虚线4为给定参考转速。传统PI控制达到稳态的时间较长,初始阶段脉动较大,一般模糊PI控制较传统PI控制,有很大改进,稳态误差减小,达到稳态的时间较短,而改进的模糊PI控制相对于前两者能够较好地控制永磁同步电机转速跟踪参考转速,控制稳态误差更小,动态响应更强,电机启动阶段性能更优越。当在t=0.07 s时突加负载转矩为10 N·m时,改进的的模糊PI控制较传统PI控制与一般模糊控制恢复过程更快。
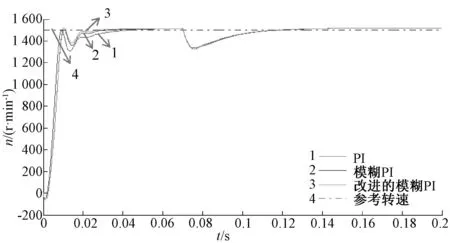
图5 转速与时间
当给定负载转矩为为10N·m时,由下图6电机电磁转矩曲线可以看出,在启动时刻电磁转矩波动量最大的是传统PI控制,对应图6中曲线5。曲线6与曲线7分别为一般模糊PI控制与改进的模糊PI控制下的电磁转矩输出曲线,改进的模糊PI控制与一般模糊PI控制相对传统PI控制波动量较小,而改进的模糊PI控制作用效果更优越。
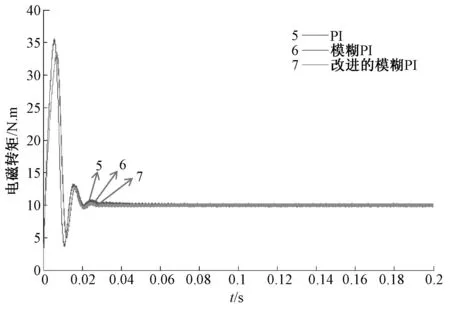
图6 电磁转矩与时间
4结论
本文重点对比分析了三种不同控制方法下永磁同步电机电磁转矩与转速响应变化。仿真结果表明,提出的改进模糊控制器较传统PI控制器及一般模糊控制器,永磁同步电机性能得到优化。特别是在启动阶段,永磁同步电机转速响应优化效果更为明显。
参考文献:
[1]龙明贵. 永磁同步电机矢量控制分析[D].成都:西南交通大学,2012.
[2]焦竹青,屈百达,徐保国. 一种具有高稳定性能的新型永磁同步电机调速系统[J]. 微电机,2007,40(3):44-47.
[3]焦竹青. 基于先进控制方法的永磁同步电机性能优化[D].无锡:江南大学,2008.
[4]李芳,王毓顺,张家瑞. 基于模糊PI控制的永磁同步电机的建模与仿真[J]. 工业控制计算机,2013,26(8):73-74.
[5]张文娟. 高性能永磁同步电机控制方法的研究[D].长沙:湖南大学,2014.
[6]王飞宇,赵朝会,田井呈,等.基于转子磁场定向的永磁同步电动机矢量控制系统对比分析[J].上海电机学院学报,2015,10(6):260-266.
[7]王宝忠,王维,王波. 基于模糊自整定PI的PMSM伺服系统的仿真研究[J]. 电力科学与工程,2013,29(7):18-22.
[8]高建兵. 基于遗传算法的模糊推理控制系统的参数优化研究[D].阜新:辽宁工程技术大学,2011.
[9]李春亚. 直驱风电组双PWM变流器控制策略研究[D].北京:北京交通大学,2015:45-50.
[10]RAO K A G,REDDY B A,BHAVANI P D. Fuzzy PI and integrating type fuzzy PID controllers of linear, nonlinear and time-delay systems [J]. International Journal of Computer Applications, 2010,1 (6): 41-47.
《电力科学与工程》
欢迎投稿,欢迎订阅
投稿网址:http://www.dlkxygc.com
The research of PMSM Vector Control System Based on Improved Fuzzy Control
XU Benben1, ZHOU Zhifeng1, HUO Wenming1, YANG Enxing2(1. School of Electrical Engineering, Shanghai DianJi University, Shanghai 200230, China; 2. Shanghai Electric Power Transmission & Distribution on Group Technology Center, Shanghai 200042, China)
Abstract:On the basis of traditional PI control and fuzzy PI control method, according to the related theories of Clarke and Park transformation, SVPWM and field oriented control, an improved fuzzy PI control method to enhance the performance of the control system was proposed in this paper. A simulation model of the control system was developed in Matlab/Simulink and comparative analysis for some important performance of PMSM was conducted. The Simulation results demonstrate that the control system has more strong adaptability, robustness and anti-interference, and could track the set speed quickly. Moreover, the output torque ripple of the PMSM is smaller when using the improved Fuzzy-PI controller.
Keywords:PMSM;vector control; fuzzy-control; Simulink
中图分类号:TM73
文献标识码:A
DOI:10.3969/j.issn.1672-0792.2016.03.001
作者简介:徐奔奔(1990-),男,硕士研究生,主要研究方向为电力电子与电力传动,E-mail:13122608568@163.com。
收稿日期:2016-01-22。

