基于Comsol的离相封闭母线短路电动力的计算

仲留寄, 王金娥

(苏州大学 机电工程学院, 江苏 苏州215006)



基于Comsol的离相封闭母线短路电动力的计算

仲留寄, 王金娥

(苏州大学 机电工程学院, 江苏 苏州215006)

摘要：为了避免母线短路过程中所产生的短路电动力使电气设备受到严重损坏,需要精确计算导体所受到的短路电动力。通过有限元软件Comsol对离相封闭母线的三相短路电动力进行详细计算，分析了最大短路电动力发生的时刻及其磁场分布，并与电动力的传统计算方法进行了比较，结果得知有限元法更接近母线导体的实际受力状况。

关键词：电动力；封闭母线；有限元；电磁场

0引言

电力系统的事故大部分由短路引起。常见的短路类型有三相短路、两相短路、两相不同接地点短路和单相接地短路。通常三相短路较其他类型的短路引起的后果更为严重，短路电流可能达到工作电流的十几倍，其产生的热效应和力效应使电气设备受到严重损坏。为了避免母线导体受到很大的短路电动力而发生形变引发安全事故，精确计算导体短路电动力显得至关重要[1,2]。

本文采用有限元法求解三相电动力的值，并与传统的公式法计算结果进行比较，同时分析了最大短路电动力发生的时刻及其磁场分布。

1模型图形的建立

一般三相管型母线的排列形式是三根管型母线导体在同一平面内相互平行。由于母线基本都是同轴圆柱，而短路电动力的计算量又比较大，为了使模型简化，文章采用二维平面模型，见图1。

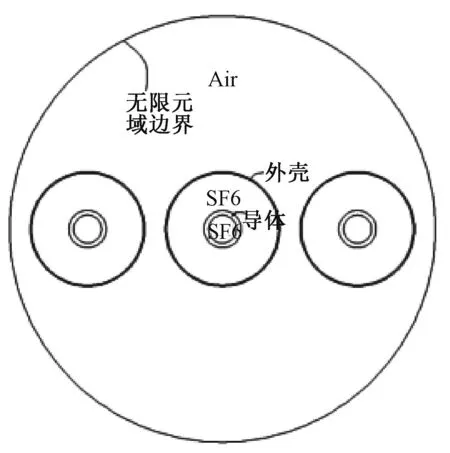
图1　离相封闭母线二维平面模型

二维模型由a、b、c三相组成，每相由铝导体、铝外壳组成、导体内的SF6气体、铝外壳内的SF6气体、铝外壳外部的Air气体组成。

计算与仿真模型的主要尺寸与参数如表1。

2有限元计算法

2.1电磁场模型、边界条件及前处理

本文主要使用Comsol Multiphysics中的“磁场”物理量及瞬态求解器，用带有时间t的变量模拟三相短路电流。如图1所示，在Comsol Multiphysics中建立在X-Y平面的2D模型，三相母线通过三相电流，相位相差120°(左边导体为A相、中间导体为B相、右边导体为C相)。

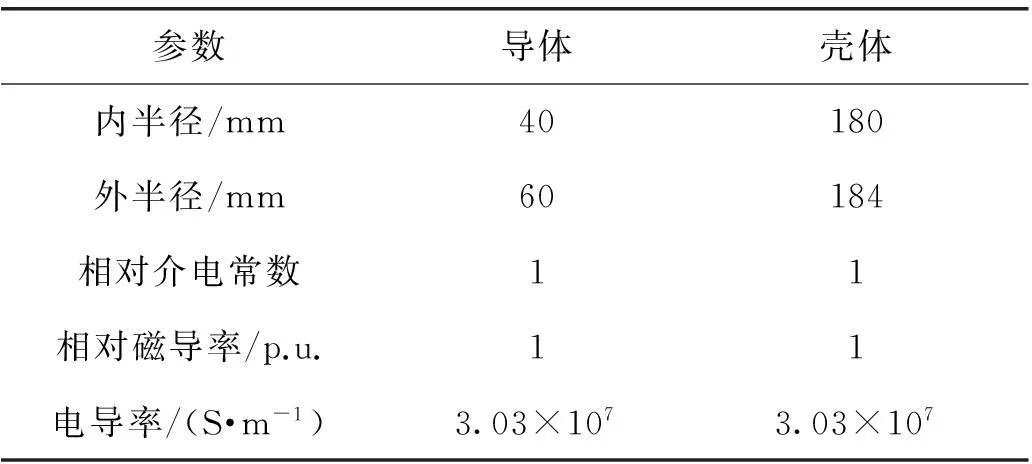
表1　模型的主要尺寸与参数

注：相间距设为500 mm

短路电流随时间的变化规律而变化的公式如下：

(1)

式中：I(t)为随时间变化的短路电流，A;Im为额定短时耐受电流的峰值，A；Ta为直流分量衰减常数，45 ms。

将A、B、C瞬态相电流分别加载到A、B、C导体上[3]。

A相电流：

B相电流：

(2)

C相电流：

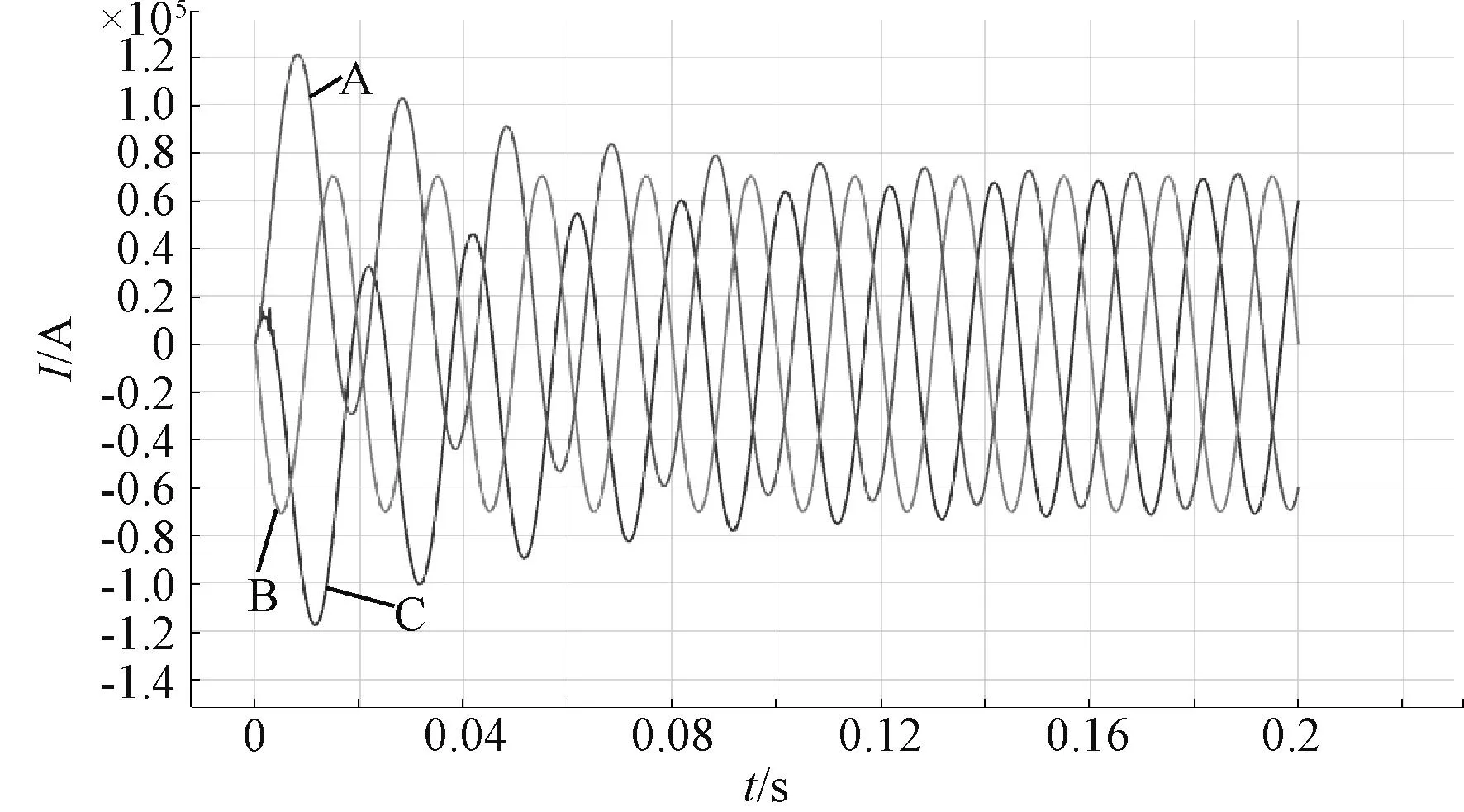
图2　三相短路电流

通过公式仿真得出图2所示的三相短路电流，A、B、C三相的初始相角相差120°，在短路前期，电流幅值最大，此阶段的短路电动力非常大，随着时间的推移，从图2中明显可以看出三相的电流幅值趋向平缓，并且幅值基本相同，所以短路电动力最大值发生在短路前期。

2.2网格的划分和求解器的设置

使用常规的母线截面的离散化在进行常规的瞬态模型求解时，会发生计算缓慢、在求解前期收敛后期发散以及求解报错等问题。本文主要通过“边界层”、“映射”等方式进行模型的离散化。

图3所示为2d模型的整体的离散化。如图4所示，由于壳体内外部都是流体，所以壳体内外壁使用了“边界层”来确定网格的形状。如图5所示，由于无限元域属于非重要计算部分，为了增加计算速度，使用“映射”进行网格的划分。从图3中可以看到导体属于重要求解域所以网格划分比较密集从而增加求解精度。

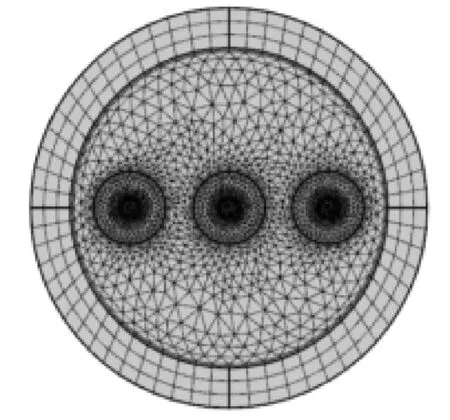
图3　整体离散化

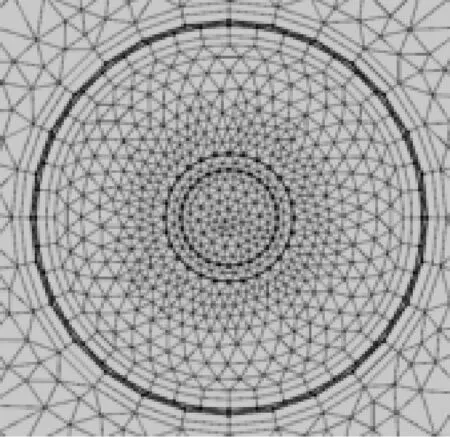
图4　壳体内外壁的离散化

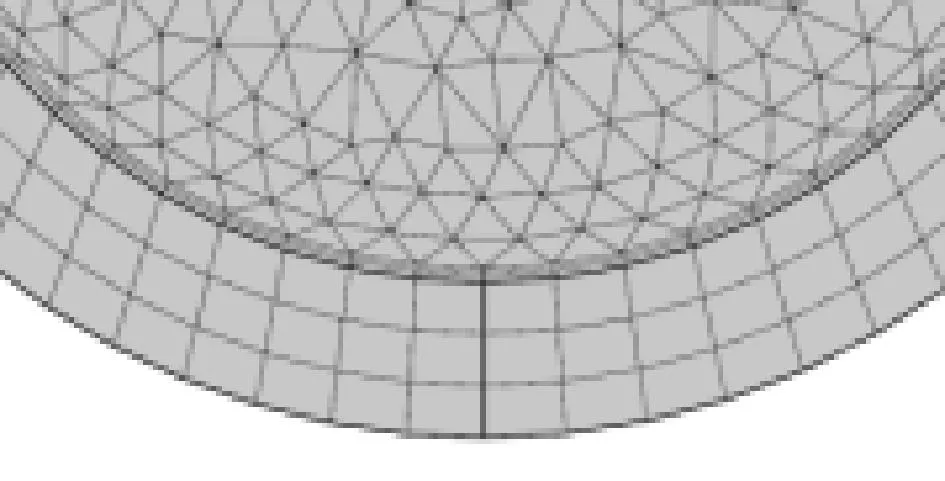
图5　无限元域的离散化

对瞬态求解器缺省值进行修改设置，设置求解时间为0.2 s，时间步长为0.000 2 s；应变量：磁向量位能：0.001；瞬态求解器：时间步长方法：广义α，求解器采用的步长：中级，放大高频：0.86。

2.3求解分析

求解完成后，对三相分别进行电动力的面积分，求解出的三相短路电动力如图6所示。

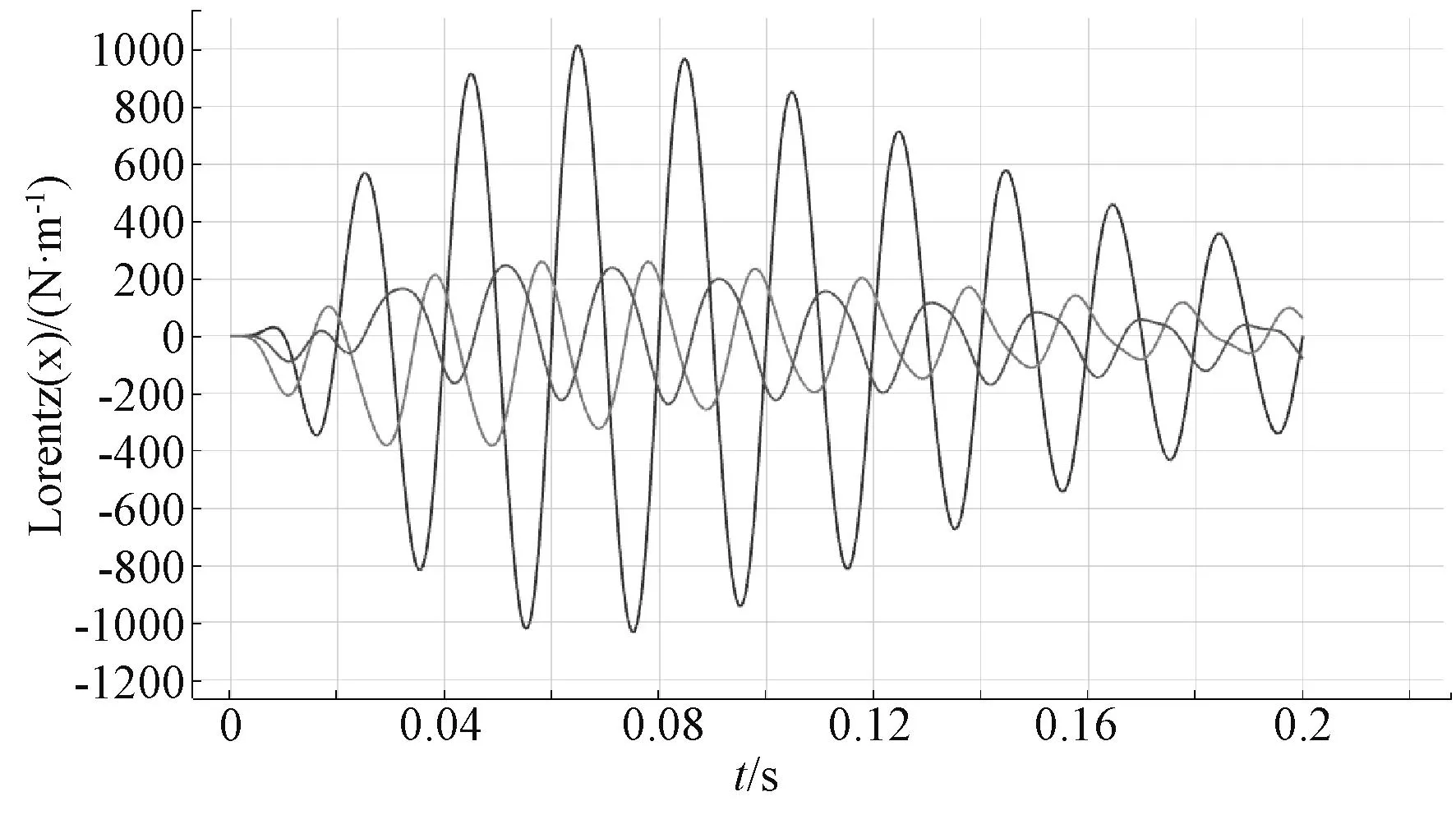
图6　三相短路电动力曲线

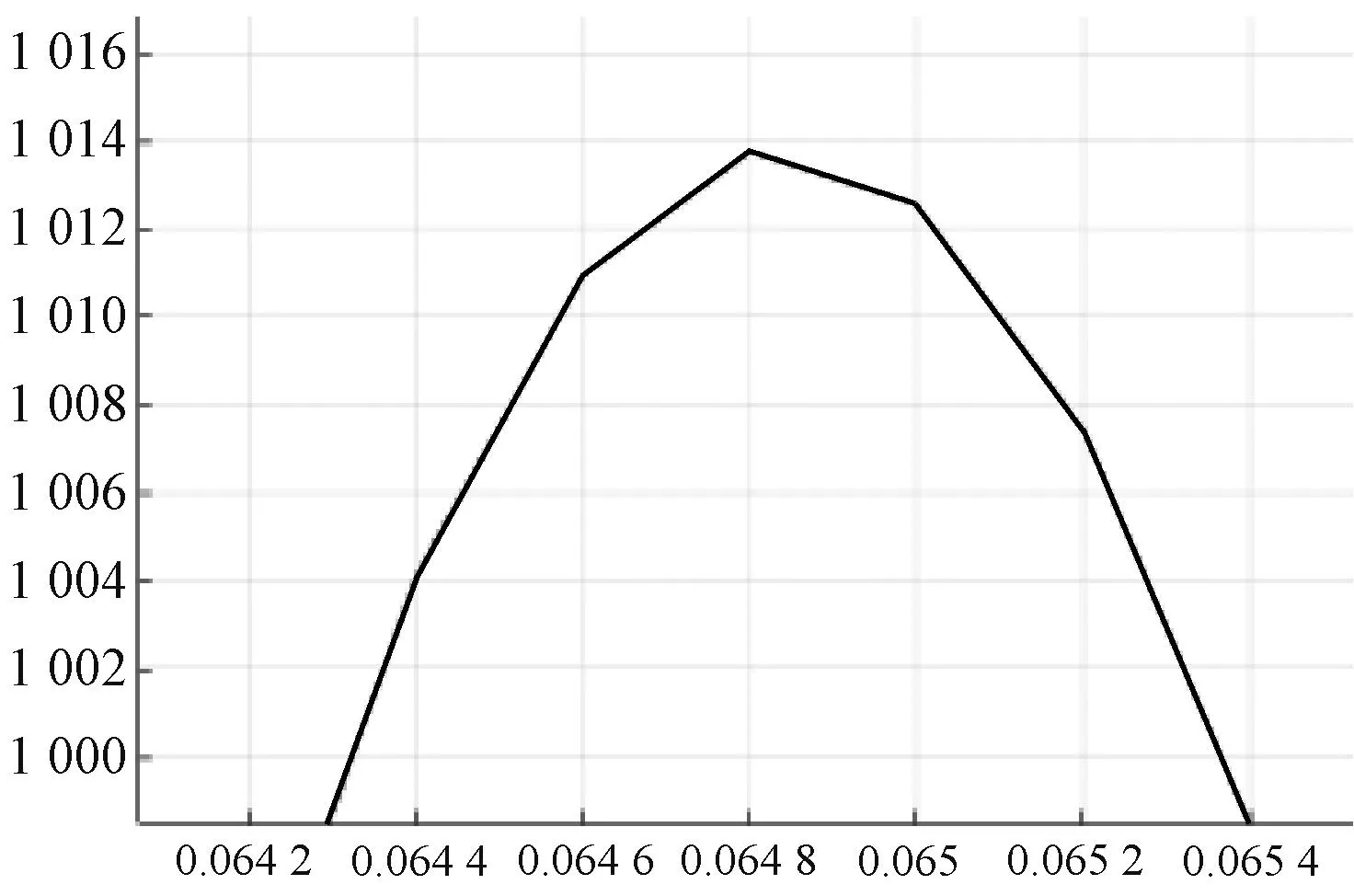
图7　B相短路电动力局部放大曲线

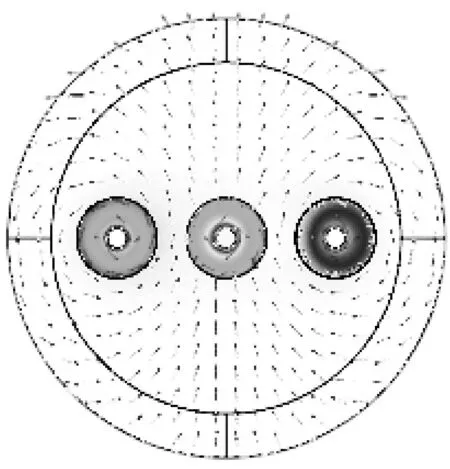
图8　短路电动力最大时磁场分布

由图6可知，很明显短路电动力最大值发生在B相，所以我们只需要对B相进行固体力学的校核即可。如图7为B相短路电动力曲线的局部放大图，可以读出B相短路电动力发生在0.064 8s时，此时短路电动力为1 014 N/m。图8为0.064 8 s时，磁场分布情况， B相受到A相与C相的相同方向的磁场[4,5]。

3电动力公式计算法

在短路状态下，工频的交流分量引起的外壳涡流和环流大体上与交流稳态相似，会随导体电流的衰减而减少。当外壳的截面较大和在工频条件下，感应出的环流和涡流会比较接近完纯导体情况下的极限值，透入壳内的邻相磁场由于受到较充分的屏蔽，所以产生的电动力较小。直流分量则不同，由于直流分量的时间常数较大，变化速率较慢，因而电磁感应弱很多，外壳电阻的作用相对大得多，大大限制外壳的环流和涡流，因此透入壳内的邻相磁场也较大，相应的电动力也较大。对于母线电动力计算主要考虑邻相直流分量所引起的壳内磁场[6]。

在忽略交流分量的影响下，各相导体所受到别相磁场引起的电动力为：

(3)

式中：qa、qb、qc为A、B、C相单位长度导体短路电动力，N/m；μ0为真空磁导率,H/m；HRA、HRB、HRC为别相剩余电流所产生的剩余磁场强度，T；imA、imB、imC为A、B、C相短路交流电流幅值，A。

母线水平布置中,导体的最大电动力发生在中相,即B相，故在机械强度校验时仅对B相导体的电动力计算[7,8]。

涡流感应常数：

(4)

式中：μ0为真空磁导率，1.256 64×10-6T·m·A-1；δ为壳体壁厚，m；Rk为外壳平均半径，m；ρ为电阻率，Ω·m。

(5)

式中:Tm为最大电动力发生时刻,s；2.41取值为文献[9]中所示。

电动力公式：

(6)

式中：Im为短时耐受电流的最大值，A;Ka为直流屏蔽系数，0.79；Ta为直流衰减常数，0.045 s；g为重力加速度，9.8 m/s2

通过公式(2)、(3)、(4)可以计算出最大电动力和最大电动力发生的时刻：

通过公式法解得最大短路电动力为981 N/m，最大短路电动力发生时刻为0.063 7 s。通过与有限元法进行比较：最大短路电动力的误差为3.2%，最大短路电动力发生时刻的误差为1.7%[10]。

4结论

(1)有限元法求出的最大电动力较公式法求解的数值大。这是由于公式法计算过程中忽略了别相母线短路电流的交流分量对B相母线的磁场影响，而有限元法更接近母线导体的实际受力，所以基础性研究最好使用有限元计算法计算最大短路电动力的值[11]。

(2)通过有限元法求解，可以方便得出任意时刻的短路电动力和磁场分布情况，能够为电动力工程计算和分析提供参考价值。

参考文献:

[1]吴励坚. 大电流母线的理论基础与设计 [M]. 北京：水利电力出版社，1985.

[2]孔庆东. 大电流母线的设计、制造及安装[M]. 北京：水利电力出版社，1988.

[3]范建斌. 气体绝缘金属封闭输电线路及其应用 [J].中国电力，2008,41(8)：38-43.

[4]高凯，李莉华. 气体绝缘输电线路技术及其应用[J]. 中国电力，2007，40(1)：84-88.

[5]THOMAS HILLERS，et al. Gas insulated transmission lion [J]. IEEE Power Engineering Review,2000(9).

[6]WAIANAE Y,MORIETAL S,NINOMIYA K,et al.Construction of first Gas insulated transmission lion in Japan [J]. IEEE Transaction on Power Apparatus & Systems, 1981,pas-100(10):4319-4329.

[7]SABOT A.Insulation Co-ordination procedure for 420kV gas insulated lines(GIL) [A].High Voltage Engineering,1999.Eleenth International Symposium on(Conf.Publ.No. 467) [C]. 1999.

[8]黎斌. SF6高压电器设计[M].北京：机械工业出版社，2009.

[9]发电教研大电流母线科研小组.全连外壳式分相封闭母线在短路时壳内磁场和母线导体所受电动力的分析和计算[J].西安：西安交通大学学报，1974.

[10]罗学琛. SF6气体绝缘封闭组合电器(GIS)[M]. 北京：中国电力出版社，1999.

[11]RUAN Quanrong,et al. High power transmission of underground hydropower station 207 m vertical installation of 800kV GIL [J].Third Inernational Conference and Exhibition on Water resources and renewable energy development in Asia. Malaysia,2010.

Calculation on Short-circuit Electrodynamic Force of Isolated-phase Bus Using Comsol

ZHONG Liuji，WANG Jine(School of Mechanical and Electric Engineering of Soochow University,Suzhou 215006，China)

Abstract：According to the fact that the electromagnetic force can cause severe damage to the electrical equipment, some research has been done on the precise calculation of electromagnetic force generated during the bus short-circuit process in this paper. Based on the finite element software Comsol, three-phase short-circuit electromagnetic forces of isolated phase bus are computed, and the moment of maximum short-circuit electromagnetic force as well as the magnetic field distribution is analyzed. Compared with the traditional calculation methods, the results obtained by applying finite element method is more accurate.

Keywords：electrodynamic force；isolated-phase bus；finite element；electromagnetic field

中图分类号:TM154

文献标识码:A

DOI:10.3969/j.issn.1672-0792.2016.03.005

作者简介：仲留寄(1989-)，男，工程师，主要从事高压输电管道和高压复合套管的研发工作,E-mail:1006494699@qq.com。

收稿日期：2015-12-21。