国际贸易均衡的立体几何演绎及数学证明*

许晓军， 袁　璐， 袁　辉

(沈阳工业大学 a. 商贸学院， 辽宁 辽阳 111003， b. 管理学院， 沈阳 110870)



国际贸易均衡的立体几何演绎及数学证明*

许晓军a， 袁璐b， 袁辉a

(沈阳工业大学 a. 商贸学院， 辽宁 辽阳 111003， b. 管理学院， 沈阳 110870)

摘要：经济学均衡包括交点均衡、驻点均衡和相切均衡。局部均衡都为交点均衡，一般均衡都为相切均衡。国际贸易理论研究一般均衡，所以国际贸易均衡大多为相切均衡。可以运用平面几何方法和立体几何方法理解国际贸易均衡，但立体几何方法更具有动感。考察国际贸易均衡的最佳方法是数学的“目标函数约束条件”方法。运用图形法和数学法理解国际贸易均衡时，应注重思考它们的经济学含义。

关键词：国际贸易； 贸易均衡； 生产可能性边界； 相对价格； 无差异曲线； 预算线； 立体几何

“均衡”是经济学追求的永恒。何穗和江胶宁(1993)运用数理经济学方法对无限维商品空间的一般经济均衡理论进行了数理推理[1]。江胶宁(1994)对一般经济均衡形成与发展的数学公理方法进行了研究[2]。罗嗣红(1996)对马克思的宏观经济均衡理论与凯恩斯总体经济均衡理论进行了详细对比研究[3]。常婕(2007)对马克思经济均衡思想与瓦尔拉斯均衡进行了对比研究[4]。于立新和王栋从经济结构角度探究中国内外失衡，认为应该采取结构调控政策[5]。刁伟涛(2006)认为，经济学的均衡范式是“半机制”，片面强调负反馈机制[6]。郭其友(1997)对经济学均衡论与非均衡论进行了深入探讨[7]。许晓军、袁辉和宁凯(2014)运用机会成本递减对比较优势势力和规模经济势力的均衡关系进行了探讨[8]。许晓军(2014)首次提出了比较优势边界概念，深入探讨了比较优势国际贸易均衡[9]，并提出了贸易曲面概念，建立了比较优势的国际贸易均衡模型[10]。

图形是研究经济学非常重要的工具。王兴德(2012)利用可调图形来阐释动态经济学原理，激发了读者的浓厚兴趣[11]5。王则柯(2012)主张经济学教材应该运用图形表达经济学原理，“几何地”学习经济学，就像学会游泳一样，不容易忘记[12]11。国际贸易均衡理论主要包括比较优势引发国际贸易的古典贸易理论(Adam Smith，1776[13]；David Ricardo，1817[14])和要素禀赋理论(Heckscher，1919；Ohlin，1924[15]；Paul A.Samuelson，1949[16]；Leontief，1953[17])；规模经济引发国际贸易的新国际贸易理论(Kemp，1964[18]；Krugman，1979[19]；Helpman，1985[20])以及异质企业动态模型(Marc J.Melitz，2003[21])，见图1。

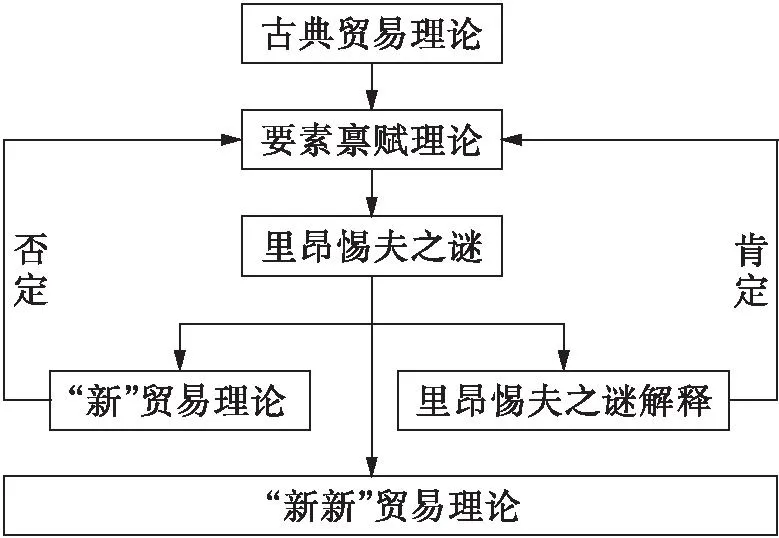
图1　国际贸易理论发展框架

一、经济学“均衡”的本质

经济学将“均衡”作为最主要目标进行研究。经济学家通过“函数最大值或者函数最小值”来推出“均衡”。例如，在消费理论里，通过“效用最大”推出消费者均衡，进而推出消费者需求曲线d，由此通过水平相加推出市场需求曲线D；在生产理论里，通过“利润最大”推出厂商短期供给曲线SS=SMC和长期供给曲线LS=LMC。无论在消费理论里的“效用最大”，还是生产理论里的“利润最大”，换成数学语言来表达，就是计算效用函数和利润函数的最大值，而计算函数最大值的方法是通过效用函数和利润函数的一阶导数计算出驻点。所以，从这个角度来说，经济学里“均衡”的本质为“驻点”。同时，对于局部均衡里的均衡，例如在完全竞争市场里，需求曲线D与供给曲线S的交点为“均衡”。在宏观经济学里，通过凯恩斯交叉图、IS曲线和LM曲线以及AD曲线和AS曲线的相交来确定“均衡国民收入y”。所以从这个角度来说，均衡为“交点”。对于一般均衡里的均衡，例如无差异曲线与预算线相切确定消费均衡，等产量线与成本线相切确定生产最优组合，则均衡为“切点”。从上述讨论可以看出，经济学里的均衡即“驻点”、“交点”和“切点”(见图2)。一般而言，由“切点”确定的均衡可以看作带有约束的目标函数极值问题，即条件极值问题。这样，将建立的拉格朗日函数看作无条件极值问题，通过偏导数计算出驻点，即为均衡点。所以“切点”均衡是特殊的均衡。

图2　均衡的本质

二、国际贸易生产均衡的平面演绎及不足

国际贸易理论是经济学的重要组成部分。但是，国际贸易理论更多地应用的是一般均衡分析，这样也就决定了其均衡一定为“切点均衡”。古典贸易理论、要素禀赋理论和新国际贸易理论等都是运用生产可能性边界、社会无差异曲线以及相对价格线工具论证自由贸易好于保护贸易的。下面以生产均衡点为例进行论述。以比较优势为核心的古典贸易理论和要素禀赋理论以机会成本递增和机会成本不变为基础，认为生产可能性边界PPF为向外凸的曲线和一条直线，见图3。

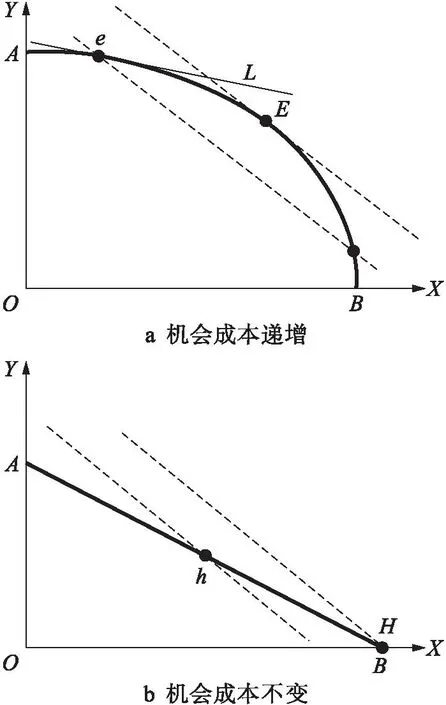
图3　机会成本递增和不变条件下的生产可能性边界

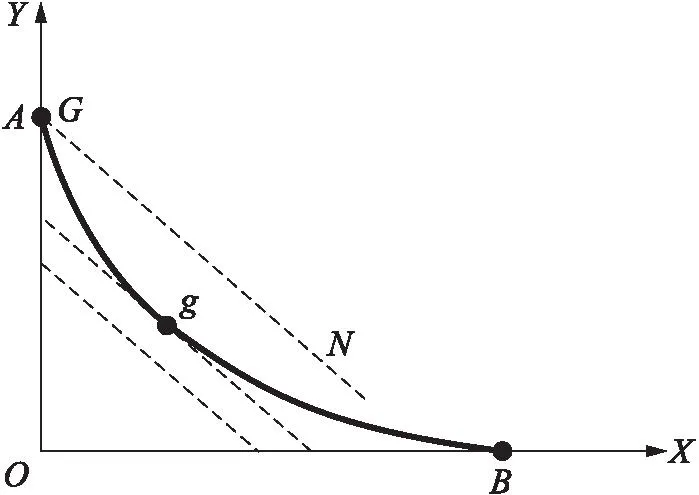
图4　机会成本递减条件下的生产可能性边界

另外，也可以运用机会成本方法理解均衡g的不稳定性，见图5。X商品由数量1增加到数量2时，放弃的商品Y数量为Y1-Y2；X商品由数量2增加到数量3时，放弃的商品Y数量为Y2-Y3。很显然，Y1-Y2>Y2-Y3，即随着X商品数量向右移动，所放弃的商品Y数量越来越少。所放弃的商品Y数量可以看作将相同资源用于X商品生产而不能用于商品Y生产的成本，称为生产X商品的机会成本。这样，X商品数量向右移动的过程可以看作其机会成本递减的过程。所以X商品数量增加所花费的成本越来越少，生产可能性边界上的点不稳定，会一直向右移动，直到端点B。同理，生产可能性边界上的点也可以随机向端点A移动。

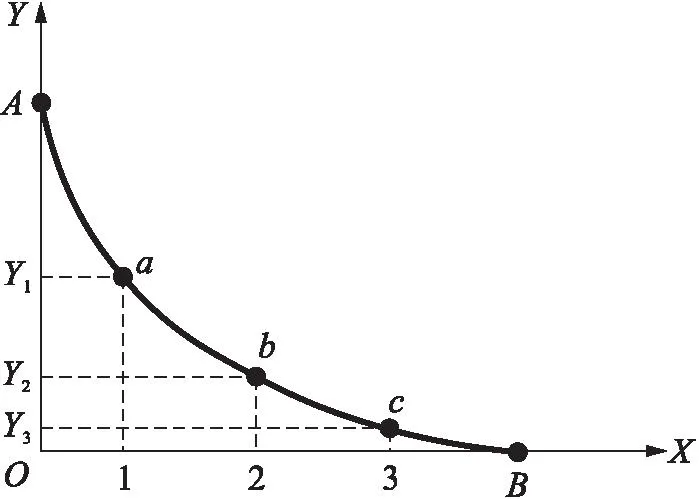
图5　机会成本递减条件下均衡的不稳定性

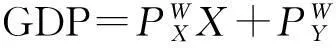
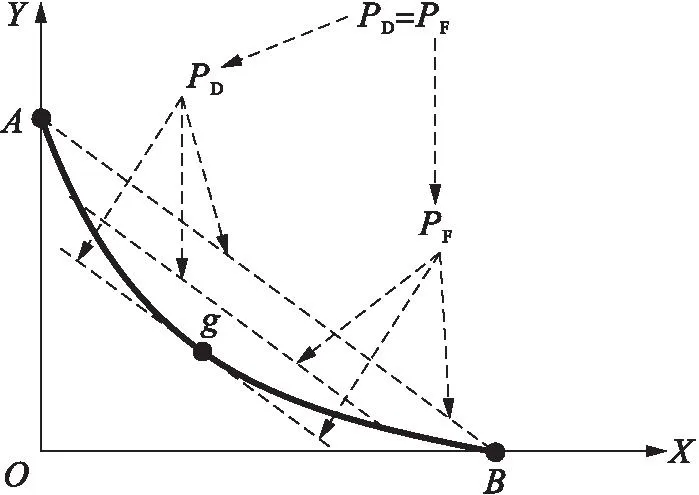
图6　机会成本递减条件下的国际贸易起因(特殊情况)

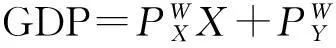
图7　机会成本递减条件下的国际贸易起因(一般情况)

如果放松一下条件，本国D和外国F封闭条件下的相对价格PD≠PF，则会产生比较优势，见图8。这样，规模经济与相对价格差会同时起作用，即规模经济和比较优势会让均衡从h和g点随机向生产可能性边界的两个端点移动。此时，直线AB即为开放条件下的相对价格线，贸易后两个国家福利也都会增加。当然，也可以形成与图7相似的“平行”开放条件下的相对价格线，两个国家福利也都会增加。

图8　规模经济与比较优势引发国际贸易

大多数经济学教材、论文和著作都是从平面几何的角度来论证均衡的。这样缺少了动感和立体感，掩盖了知识的相关内容。所以，从“立体”的角度来演绎均衡的本质更具有理论意义。

三、国际贸易生产均衡的立体几何演绎

为了与国际贸易生产均衡的平面演绎相一致，假设GDP平面为向右上方倾斜的水平面，生产可能性边界为垂直于XOY平面的“柱面”。在国际贸易生产均衡的平面演绎里，GDP是一条斜率为负的直线，对应于不同的斜率表现出不同的倾斜程度。在国际贸易生产均衡的立体几何演绎里，GDP为平面。可以想象，无论GDP的平面是平坦还是陡峭，与XOY平面的交线都为平面演绎里斜率为负的GDP直线。所以，在国际贸易生产均衡的立体几何演绎里，GDP平面与XOY平面的夹角大小与结论无关，可以是任意夹角。

机会成本递增条件下生产可能性边界的立体演绎如图9所示。

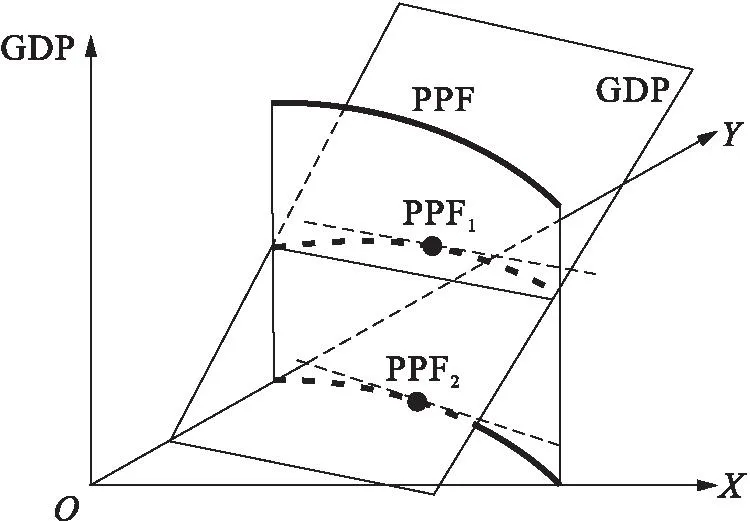
图9　机会成本递增条件下生产可能性边界的立体演绎

图9中，垂直于XOY平面、平行于纵轴的柱面为生产可能性边界PPF面，与生产可能性边界PPF面相交的平面GDP是国民收入面。GDP平面越往上，表示GDP水平越高。当GDP平面与PPF柱面只有一个交点PPF1时，即相切时，GDP水平达到最高。将其投影到XOY平面即为PPF2，也就是图3中向外凸的生产可能性边界情况。此为封闭条件均衡情况。若在开放条件下，由于X商品和Y商品的价格发生变动，所以GDP平面会发生“旋转”，与相同的PPF柱面相切于另外一个切点，形成开放条件下的均衡，此时PPF没有变动。如果考虑生产技术提高，那么PPF柱面会向外移动，形成新的封闭条件和开放条件下的生产均衡点。

机会成本不变条件下生产可能性边界的立体演绎如图10所示。

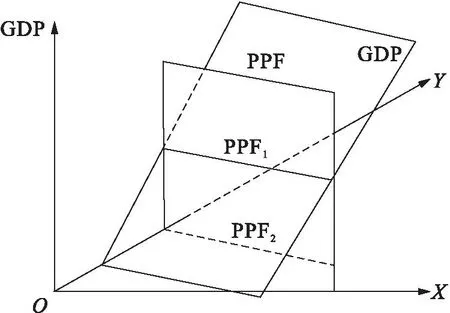
图10　机会成本不变条件下生产可能性边界的立体演绎

图10中，垂直于XOY平面、平行于纵轴的平面为生产可能性边界PPF面，与生产可能性边界PPF面相交的平面GDP是国民收入面。GDP平面越往上，表示GDP水平越高。当GDP平面与PPF平面交线为一条直线时，有无数个切点，即有无数个均衡点。将其投影到XOY平面，即为XOY平面内的PPF，此时GDP线与PPF线重合。在开放条件下，GDP平面会发生“旋转”，与PPF线相交于端点，GDP水平达到最高，也就是图3的水平直线的生产可能性边界情况。

机会成本递减条件下生产可能性边界的立体演绎如图11所示。

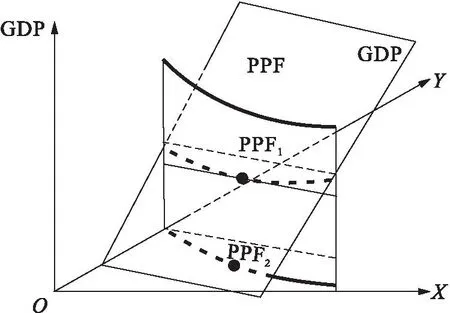
图11　机会成本递减条件下生产可能性边界的立体演绎

图11中，垂直于XOY平面、平行于纵轴的柱面为生产可能性边界PPF面，与生产可能性边界PPF面相交的平面GDP是国民收入面。GDP平面越往上，表示GDP水平越高。当GDP平面与PPF柱面只有一个交点PPF1时，即相切时，GDP水平没有达到最高。如果调整商品X和Y的生产数量，则GDP会继续增加，直到PPF端点处达到最高。将其投影到XOY平面即为PPF2，也就是图4所示的生产可能性边界情况。如果考虑生产技术提高，那么PPF柱面会向外移动，形成新的生产均衡点。

从以上讨论可以看出，对于机会成本递增和不变的情况，发生国际贸易的原因是GDP平面发生“旋转”，即商品X和Y的价格发生变动。更进一步来说，是由于比较优势引发的国际贸易。但是，对于机会成本递减的情况就不一样了，由于规模经济造成“切点”不稳定，在没有比较优势的条件下也会发生国际贸易。

四、国际贸易生产均衡的数学证明

可以将上面生产均衡的图形演绎转换为数学推导过程。从上面的图形演绎过程可以看出，GDP为目标函数，生产可能性边界为约束条件。据此建立数学模型，即

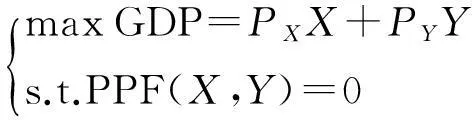
(1)

建立拉格朗日函数，即

L(X，Y，λ)=PXX+PYY+λPPF(X，Y)

(2)

则有如下方程组成立，即

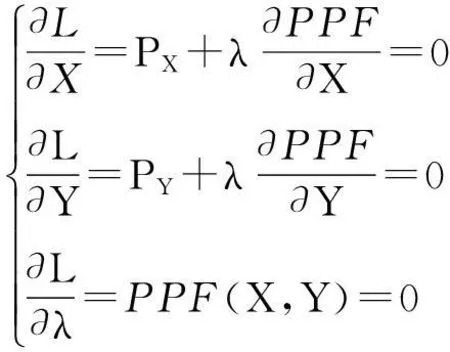
(3)

所以

(4)

同时，可以通过生产可能性边界的隐函数PPF(X，Y)=0计算导数，则有如下等式成立，即

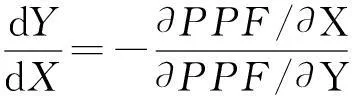
(5)

所以

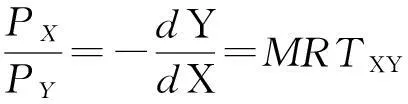
(6)

另外，将生产可能性边界的显性函数作为约束条件，也可以推出同样的结论，即

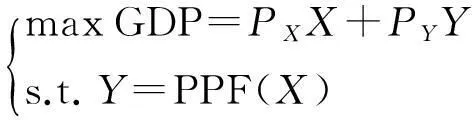
(7)

建立拉格朗日函数，即

L(X，Y，λ)=PXX+PYY+λ(Y-PPF(X))

(8)

则有如下方程组成立，即

(9)

所以

(10)

可以看出，通过数学方法推出的均衡条件在任何条件下都成立。但是在机会成本递减的生产可能性边界条件下，极值不是在驻点处取到而在端点处取到，所以机会成本递减条件下的均衡具有不稳定，会向端点处移动。因此，从数学角度看，比较优势与规模经济对于国际贸易的发生而言具有统一性。

五、国际贸易消费均衡的立体几何演绎

1. 无差异曲线的立体演绎

将微观经济学里的无差异曲线进行加总，便为国际贸易理论里的社会无差异曲线，所以微观经济学中无差异曲线的立体几何演绎非常重要。假设消费者消费X和Y两种商品，给该消费者带来的效用为U。问题在于，不同的消费者消费相同数量的同质商品X和Y，他们的感受即效用U是不同的，为什么呢?原因在于他们的偏好不同。消费者偏好就像数学里的对应法则f，所以消费者偏好不同，那么效用就不同。这样会形成不同的效用曲面U=f(X，Y)，如图12所示。

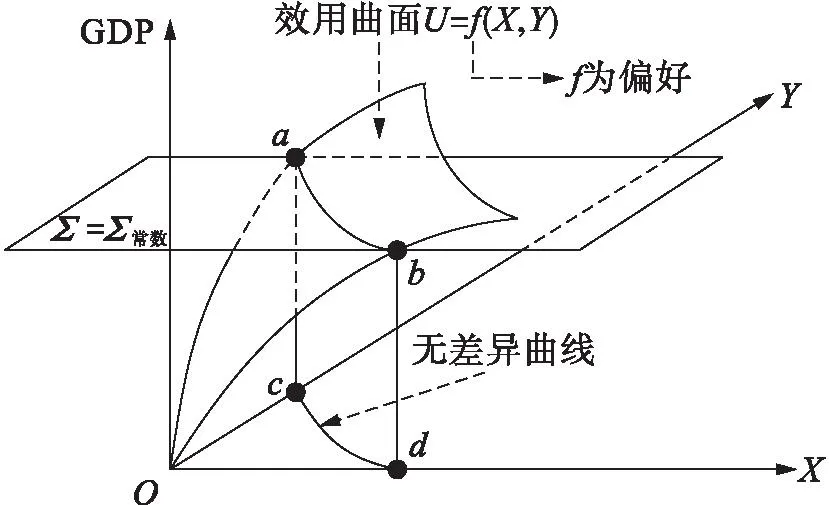
图12　无差异曲线的立体演绎

取一个常数，会在空间形成一个平面Σ=Σ常数，该平面与消费者效用曲面U=f(X，Y)相交于ab曲线。此时，ab曲线上任意一点高度都相等，代表着该消费者此时消费某组X和Y商品组合的效用水平。由于在空间研究效用不方便，所以将ab曲线投影到XOY平面上，形成cd曲线，即该消费者的无差异曲线。cd无差异曲线任意一点的效用相同，因为其来源于ab曲线，而ab曲线上任意一点效用都相等。

可以想象，消费者偏好f不同，则该消费者的效用曲面U=f(X，Y)就会“旋转”和“平移”，那么形成的无差异曲线也会有所不同。

2. 国际贸易消费均衡的数学证明

仔细思考图3、4，当一个国家的生产点确定以后，该国的收入线GDP=PXX+PYY便会“不动”，此时可将该国的收入线看作国民收入预算线。在该预算约束线下，引进该国的社会无差异曲线。此时，该国的预算约束线为该国的约束条件，目标函数为该国的福利水平达到最大。可以想象，国民收入线GDP=PXX+PYY“不动”让该国的社会无差异曲线越高越好，直到与国民收入线相切，达到“切点均衡”。可以将这个消费均衡过程写成数学模型，即

(11)

建立拉格朗日函数，即L(X，Y，λ)=f(X，Y)+λ(GDP-PXX-PYY)

(12)

则有如下方程组成立，即

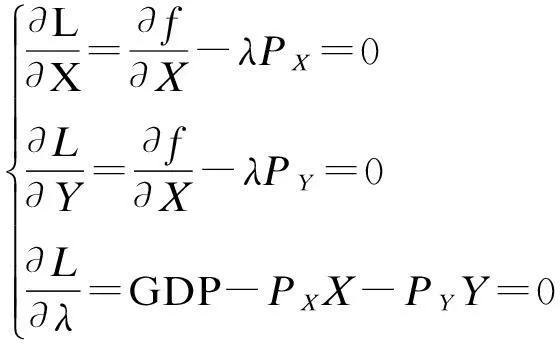
(13)

所以，国际贸易消费均衡条件为

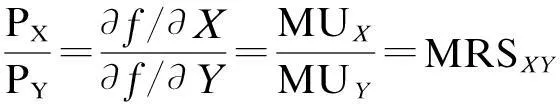
(14)

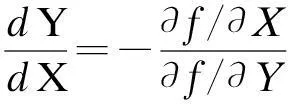
六、结论

参考文献：

[1]何穗，江胶宁.无限维商品空间的一般经济均衡理论 [J].经济数学，1993(1)：62-69.

[2]江胶宁.一般经济均衡理论的形成与发展：经济理论研究中的数学公理化方法 [J].华中师范大学学报(哲学社会科学版)，1994(1)：26-30.

[3]罗嗣红.马克思的宏观经济均衡理论与凯恩斯总体经济均衡理论的比较 [J].中南财经大学学报，1996(5)：10-13.

[4]常婕.对马克思经济均衡分析思想的认识：兼论瓦尔拉斯均衡分析思想 [J].广西教育学院学报，2007(4)：71-74.

[5]于立新，王栋.我国内外经济均衡发展战略与宏观调控 [J].宏观经济研究，2012(5)：10-17.

[6]刁伟涛.均衡范式：主流经济学的半机制 [J].经济学家，2006(1)：47-53.

[7]郭其友.当代西方经济学均衡论与非均衡论之争及实质 [J].厦门大学学报(哲学社会科学版)，1997(4)：63-67.

[8]许晓军，袁辉，宁凯.基于比较优势及规模经济的国际贸易万能公式探讨 [J].北京工业大学学报(社会科学版)，2014(1)：30-34.

[9]许晓军，袁辉，宁凯.比较优势边界与国际贸易政策研究 [J].沈阳工业大学学报(社会科学版)，2014，7(4)：331-336.

[10]许晓军.基于贸易曲面的国际贸易均衡模型与贸易政策探讨 [J].石家庄经济学院学报，2014(6)：12-18.

[11]王兴德.动态经济学图解：用可调图形来阐释动态经济学原理 [M].上海：上海财经大学出版社，2012.

[12]欧瑞秋，王则柯.图解经济博弈论 [M].北京：中国人民大学出版社，2012.

[13]亚当·斯密.国民财富的性质和原因研究 [M].北京：商务印书馆，1983.

[14]大卫·李嘉图.政治经济学及赋税原理 [M].北京：商务印书馆，1979.

[15]罗伯特·C·芬斯特拉.国际贸易 [M].北京：中国人民大学出版社，2011.

[16]Paul A S.International factor-price equalization once again [J].The Economic Journal，1949，59(1)：181-197.

[17]Wassily L.Domestic production and foreign trade：the American capital position re-examined [J].Proceedings of the American Philosophical Society，1953，97(4)：332-349.

[18]丹尼斯·R·阿普尔亚德.国际经济学 [M].北京：机械工业出版社，2010.

[19]保罗·克鲁格曼.克鲁格曼国际贸易新理论 [M].北京：中国社会科学出版社，2001.

[20]赫尔普曼，克鲁格曼.市场结构和对外贸易 [M].上海：上海人民出版社，2009.

[21]Marc J M.The impact of trade on intra-industry reallocations and aggregate industry productivity [J].Econometrica，2003，71(6)：1695-1725.

Solid geometry deduction and mathematical proof of international trade equilibrium

XU Xiao-juna, YUAN Lub, YUAN Huia

(a. School of Business, Shenyang University of Technology, Liaoyang 111003, China, b. School of Management, Shenyang University of Technology, Shenyang 110870, China)

Abstract：Economic equilibrium includes intersection equilibrium, stagnation point equilibrium and tangent equilibrium. The partial equilibrium is intersection equilibrium, and the general equilibrium is tangent equilibrium. The general equilibrium is studied in international trade theory, so most of international trade equilibrium is the tangent equilibrium. International trade equilibrium can be understood through applying the methods of plane geometry and solid geometry, in which solid geometry method is more dynamic. The best method of investigating international trade equilibrium is the “objective function-constraints” method of mathematics. When understanding international trade equilibrium by applying graphical method and mathematics method, the economic meanings of them should be paid special attention.

Key words：international trade; trade equilibrium; production possibilities frontier; relative price; indifference curve; budget line; solid geometry

中图分类号：F 740

文献标志码：A

文章编号：1674-0823(2016)02-0125-07

doi：10.7688/j.issn.1674-0823.2016.02.05

作者简介：许晓军(1978-)，男，辽宁葫芦岛人，讲师，硕士，主要从事国际贸易理论与政策等方面的研究。

基金项目：辽宁省教育厅人文社会科学研究立项课题(W2013024，W2010313)； 辽宁省高校党建理论研究课题(GXDJ2014-B076)。

收稿日期：2015-09-10

(责任编辑：郭晓亮)

*本文已于2015-12-24 15∶02在中国知网优先数字出版。 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1558.C.20151224.1502.012.html