基于流抽样和LRU的高速网络大流检测算法

白 磊 田立勤 陈 超,2

基于流抽样和LRU的高速网络大流检测算法

白 磊1田立勤1陈 超1,2

1(华北科技学院计算机学院 北京 101601)

2(浙江大学机械工程学院 浙江 杭州 310058)

在高速主干网络中，随着网络链路速率的不断提高和网络流数量的增加，如何及时、准确地检测出网络中的大流信息，成为目前网络流测量的热点问题。根据传统LRU算法由于突发性大量小流导致淘汰大流的测量缺陷和网络重尾分布的特点，提出一种新的识别大流的算法——基于流抽样和LRU的大流检测算法。算法通过流抽样技术过滤大部分的小流，并通过LRU算法识别大流信息，将过滤和识别过程分离，减少小流错误淘汰大流的可能性，提高算法测量准确性。分析算法的复杂度和漏检率，并通过实际试验数据分析了算法参数配置对于大流测量的准确性的影响。理论分析和仿真结果表明，与标准LRU算法和LRU_BF算法相比，在使用相同的存储空间下，新算法具有更高的测量准确性和实用性。

网络测量 大流 抽样 哈希 近期最少使用算法(LRU)

0 引 言

网络流量测量是网络管理的基础，是分析网络业务、网络行为的重要方法。通过测量可以对数据进行分析和处理，并提取网络行为特征和规律，对网络监控、网络设计和网络规划都具有重要意义[1]。然而随着互联网的快速发展和网络新应用的不断出现，计算机网络呈现向高速化、大规模、复杂化方向发展的趋势。显著特点是产生的数据量大、数据分组到达频率高，导致单位数据分组的处理时间越来越短，对系统的存储能力、处理能力和传输能力都提出了极大的挑战，这便对网络流量处理设备提出了更高的要求。当前广泛采用的测量方法是把网络数据流归并为流(flow)，通过把数据包归并到相应流中，极大地压缩了数据量，使得网络数据的存储、处理和传输更为容易。但骨干网络在峰值下并发流的数量仍然高达几十万甚至上百万，完整保存这些流的状态需要很高的计算和存储开销。

很多基于网络流测量的研究表明，即便在不同的网络环境中，网络流的统计呈现很强的重尾分布特性。这种特性被称为“the elephants and mice phenomenon”，即大部分流(mice流)只产生很少数量的报文，而小部分流(elephant流)却产生很大数量的报文[2,3]。大流的一个显著的特性就是它们仅占总体流的数目的一小部分却产生总流量的绝大部分。这样，在实际应用中，多数情况下只需掌握占据大部分流量的大流信息即可满足需要。因此，如何利用有限的硬件资源用于大流检测，尽可能收集字节流量超过某个固定阈值的大流信息成为高速网络测量的研究热点问题。

Cristian等人首次采用“抓大放小”策略将大流检测引入流量测量领域，并提出抽样保持(sample and hold)和多级过滤(multistage Bloom filters)算法用于长流识别。前者算法简单、易于实现，但当网络流数量较多，而抽样频率较低时需维护较大的存储空间，且误差偏高；后者对存储空间需求较小，处理速度较快，但算法的错误肯定率较高，会把小流误检为大流[4]。Tatsuya等提出一种使用周期抽样识别长流的机制。这一机制的关键是在恰当地权衡错误肯定和错误否定的基础上，使用贝叶斯理论计算出抽样流的报文数的阈值，通过这一阈值可以判定其原始流是否是长流。但它的缺点是实现时精度不高，错误的肯定率和错误的否定率之间的平衡不易实现[2]。Duffield等提出由抽样流数据推断出原始流数据、获取原始流信息的思想，并提出两种推断方法：比例法和EM算法[5]。程光等提出使用积分推断法和迭代法根据未抽样流数和已抽样流数推断原始流量的统计信息[6]。使用报文抽样技术，会造成一些内在信息的损失，所以往往使用推断的方法来减少这种损失，但是这些估计方法像EM算法计算量太大，不适合数据的在线处理。Kim等提出在路由器队列管理中，利用页面置换策略LRU机制来识别持续时间长、高速率的IP流[7]。张震等提出将流识别和流过滤分开处理的方式使用Bloom Filter及LRU算法实现长流信息统计[8]。使用LRU的方法具有处理速度快、识别率高、存储空间可控等优点，但在实际测量中，当流的数量较多，某些突发性的小流有可能导致大流量对象被替换出缓存[9]，从而引起较大的测量误差。

本文根据网络流量分布的特性，提出流抽样的测量方法，并结合LRU算法实现长流识别，算法能够在使用较小的高速缓存资源情况下，精确提取大流量对象。

1 网络流的定义

网络中的“流”概念可以定义为对一个呼叫或连接的人为逻辑对应。流是流量的一部分，由起始时间和停止时间定界。与流相关的属性值(源/目的地址、分组计数、字节计数等)具有聚合性质，反映了在起始和停止范围发生的事件。由于研究背景的不同，对于流采用了不同的定义。

定义1 流是指符合特定的流规范和超时约束的一系列数据包的集合。在本文中流是指具有相同的源IP、宿IP、源端口、宿端口的按超时约束的TCP或UDP报文集合(不考虑协议)。流超时决定什么时候结束一个流，即同属一个流的相邻两个报文的到达时间间隔，在本文中流超时都设置为30秒。

定义2 大流是一段时间内某个流的长度超过事先定义的阈值TH的流。

定义3 高速网络大流监测算法的约束条件：1) 存储空间有限，用来维护摘要统计信息且所需存储空间远小于网络流空间的大小，通常只存储少量数据项的摘要信息；2) 实时处理，对每个数据项的处理时间很短，操作少而简单；3) 一次线性扫描，每个报文的到达次序完全随机，只能依序从头至尾读取一次数据流。

2 基于流抽样和LRU的大流检测算法

2.1 标准的LRU算法

LRU算法又称为近期最少使用算法，其基本原理是：维护固定大小的缓存空间，将到达的元素依次存储到缓存中，并始终保持最新到达的元素置于缓存的顶端，而最久未到达的元素则保留在缓存的最底部。当有新元素加入而缓存已满情况下，把缓存最底部的元素替换出去，并将新元素置于顶部。LRU算法在计算系统中有着广泛的应用，如内存管理、数据库缓存管理以及磁盘缓存管理等领域。

文献[7]首先将其引入网络流量测量领域，通过维护一个固定大小的LRU高速流缓存，并使用LRU思想对到达的每个分组所属的流标识进行置换。由于小流持续时间短、长度小、到达速率低，根据LRU算法总有可能被替换出去；而大流由于持续时间长、长度大、访问缓存频繁，所以往往会留在LRU 缓存的顶部，从而可以实现大流检测。但是，在实际测量过程中，当大量突发性的小流到达时，由于小流的数量较多，会充满LRU的缓存空间，这样会致大流对象被置换出LRU缓存空间。文献[7]的实验结果也表明有10%至20%的大流信息没有检测到。因此需要对传统的LRU算法进行改进，减少小流进入LRU缓存空间的概率，提高测量准确性。

2.2 流抽样机制

为解决突发性大量流信息同时到达，导致LRU算法大流漏检情况，本文提出基于流抽样的处理机制，减少大部分的小流信息进入LRU缓存的概率。流抽样的处理过程与传统的报文抽样不同，不是简单随机或周期性的抽取报文，而是根据流标识抽样情况进行抽样。其过程如下：按照概率P对链路上的报文进行周期抽样，一旦一个报文被抽取到后，其所属的流信息被标识，并哈希到内存相应位置。随后这个流所属的报文不管是否属于抽样周期，将都会被抽到，即该流的后续的每一个报文都会被处理。这样由于网络上的流统计呈现重尾分布的特性，通过抽样，可以过滤掉大部分的小流信息，减少小流进入LRU缓存空间的概率，而大流由于长度较长，其所属的报文更容易被抽取，一旦大流的某个报文被抽取到，其后续的报文都将被抽取。

实现流抽样的关键是如何识别已识别的流信息，我们使用Bloom Filter(BF)结果实现此过程。BF是用来表示一个集合的随机数据结构，它支持成员查询、随机存储[10]。其工作原理是：对于一个源串集合S={x1,x2,…,xn}，BF申请一个内存大小为m单元的存储空间A，每个单元维护一个计数器初始值置0，并使用哈希函数集合H={H1,H2,…,Hk}，每一个Hi，均是一个哈希函数。对于源串集合S中的任何一个元素xi，通过集合H中的k个独立的哈希函数映射到存储空间A中，得到k个[1，M]之间的数，并将内存空间A中的这k个对应单元比特位置1。因此Bloom Filter随机存储的过程就是通过k个哈希函数把某一元素哈希到Bloom Filter的存储空间，并把相应的位置置1的过程。当BF需要判断任一元素x′是否属于集合S中的元素时，BF对x′经k个哈希函数作用判断哈希位置是否均为1，如果是则认为x′属于集合S，否则就不是集合中的元素。然而当对x′哈希的结果均为1，而实际x′却不属于集合S时，就出现了错误的肯定。Bloom Filter错误肯定的x′属于集合S的概率，即为错误肯定率FPR(False Positive Rate)。研究表明，BF的错误肯定率满足公式fBF=(1-e-kn/m)k，其中k为哈希函数个数，n为元素个数，m为BF的存储空间数。BF存储和查找过程如图1所示。

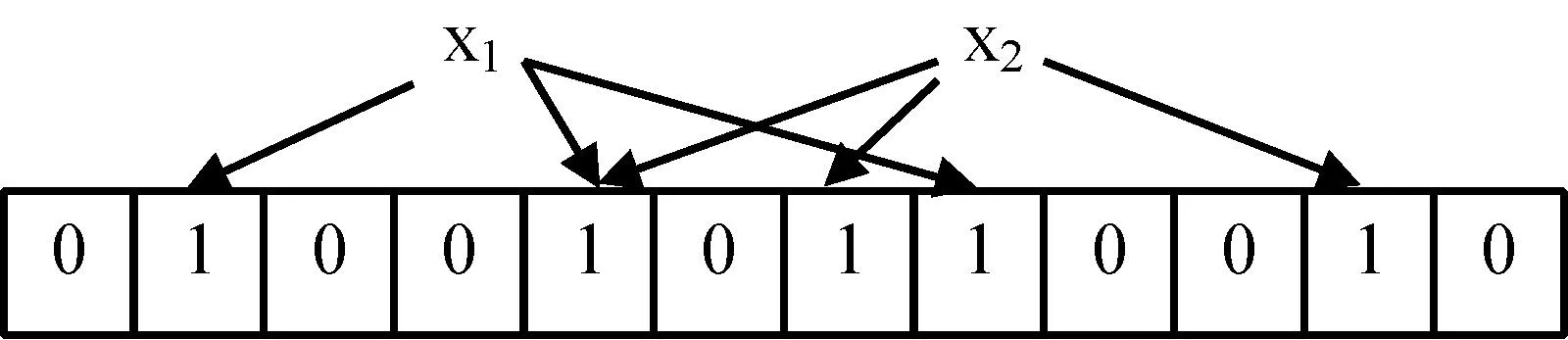
图1 标准Bloom Filter原理示意图

因此可以利用BF随机存储和查询机制判断一个流是否已被抽样，通过使用哈希函数集合H={H1,H2,…,Hk}对到达的报文的流标识(协议类型、源/宿IP、源/宿端口)xi进行作用。如果某个报文恰好属于抽样周期，或该报文所属的流已被BF存储，则抽取此报文，否则丢弃。

2.3 使用流抽样和LRU算法检测大流

基于流抽样和LRU的大流检测算法由流抽样机制和LRU算法两部分组成。流抽样机制的作用是用来过滤掉大部分的小流信息，抽取大流信息，其又分为周期抽样和BF流识别两个模块；LRU算法的作用是用来对抽取的报文实现大流检测。图2给出流抽样和LRU算法的结构示意图。

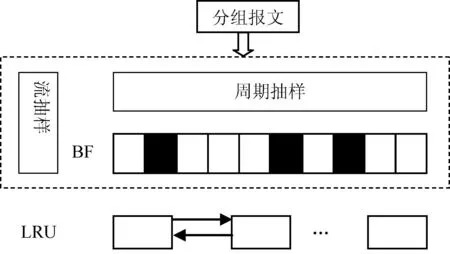
图2 流抽样和LRU算法过程原理图

算法伪码描述如下所示：

initialize (BF,LRU)

//初始化BF和LRU链表

While a packet x arrives

calculate H=h(1),h(2),…,h(k)

//计算出k 个哈希函数值

if( P ){

//如果是抽样周期

sample(x);

//抽取报文x

BF(k)+1;

//BF的k个哈希位置置为1

LRU();

//转交LRU算法处理

}else{

//非抽样周期

if(all BF(k)=1){

//判断k个位置是否为1

sample(x);

//抽取报文x

LRU();

//转交LRU算法处理

} else

discard(x);

//丢弃该报文x

}

LRU(){

//LRU算法

if(Find(x) or not full){

//如果已在LRU链表中，或链表未满时

update(count);

//流报文计数+1

setTop();

//将该流标识节点置顶

}

else

//不在链表中，且链表已满

eliminate(last);

//淘汰最后一个流节点

}

基于流抽样和LRU算法的大流检测过程：当报文到达时，首先判断该报文是否满足概率P的抽样周期，如果符合抽样周期则直接抽取此报文，并根据所属的流标识使用BF的哈希函数集在相应位置置1，并将报文转交LRU算法处理；否则如果报文不在抽样周期，则由BF判断该报文是否为已识别的流。如果属于已识别流，则抽取报文转交LRU算法处理；如果不属于任何已识别流，则丢弃该报文，继续处理下一报文。LRU算法采用散列双向链表的数据结构[11,12]，每个链表节点都存储流标识和流的报文计数器，对于采用流抽样机制抽取的每个报文，先判断该报文所属流标识是否已在链表中，如果已存在，则对应计数器加1，同时将该节点置于LRU 链表顶部；当所属流标识不在链表中，需要创建新的流量记录时，若LRU 链表已满，应根据“近期最少使用”原则，淘汰LRU 链表的最后一个流；同时，为了降低大流漏检率，在淘汰流时，需要判断其是不是已经为大流。最终输出流长度大于指定阈值的流即为需识别的大流信息。

从以上分析可以看出，流抽样和LRU算法只会处理处于抽样周期或者已抽样的流的报文。小流信息由于抽样机制，仅有满足抽样概率P的小流需要处理，大部分被丢弃掉，从而减少突发性的大量小流同时进入LRU缓存，导致错误淘汰大流的可能性。对于大流，由于长度较长，较容易被抽取，而且一旦大流的某个报文被抽取到，其后续的报文都将被抽取，这样实现抓大放小的过程。

2.4 算法分析

算法测量准确性的影响因素有两个方面，一个是BF的错误肯定率，即将某个不属于已识别的流的报文，错误识别为已识别流的报文。由公式fBF=(1-e-kn/m)k可知，当m值较大时，公式值较小，即BF转发给LRU算法的错误肯定报文数量较小，不影响LRU算法处理。影响算法准确性的主要因素是LRU算法的漏检率。

(1)

将P(F=TH)=θ/THα+1代入式(1)可得：

(2)

由于算法查找过程使用哈希函数集进行作用，BF对哈希空间的一次访问内存开销均为O(k)。由于BF使用并行散列运算，算法实际执行时间接近1次散列运算所需时间。同时，LRU 链表采用散列双向链表，使用拉链法解决散列冲突，则平均查找长度为O(1+β/2)，其中β为装填因子。

3 实验仿真

为了验证上述本文提出的流抽样和LRU算法的有效性，本文使用采集于NLANR的Trace进行仿真试验[13,14]。Traces总共报文数6 187 376个，共有68 367个流。BF使用k=6个哈希函数，存储空间大小m=216=65 536,即哈希空间为[0，65 535]。实验测量网络报文数据的原始分布如图3所示，从图中可以看出网络流的分布统计呈现重尾分布特性。

图3 实验数据网络流原始分布

图4显示当LRU算法采取固定的存储空间大小(8192)时，抽样频率变化，对算法测量不同阈值的大流准确性影响。

图4 抽样频率对算法测量准确性影响图

从图4可以看出，对于测量各种大流的阈值情况，测量准确性均随着抽样频率降低而增大。这是由于随着抽样频率降低，导致丢弃大量的报文，从而影响测量准确性。而且如果大流阈值越小(如128)，测量的准确性要比相对较大的大流阈值(如8192)低的多，这是由于长流阈值越长，对抽样频率的敏感程度越低。

由于文献[8]中验证了LRU_BF算法相对于其他类似算法如MBF算法、L_LRU算法、N_LRU算法等具有较高的精度，且使用的技术与本文类似。因此本文将基于流抽样和LRU的算法(LRU_Sample算法)与LRU_BF算法和标准LRU算法进行比较。表1-表3分别显示本文提出的基于流抽样和LRU的算法(LRU_Sample算法，抽样频率P=1/5)、标准LRU算法以及文献[8]提出的LRU_BF算法，在LRU缓存空间变化时测量不同阈值(TH)的大流的准确性比较。

表1 LRU_Sample算法(P=1/5)在

续表1

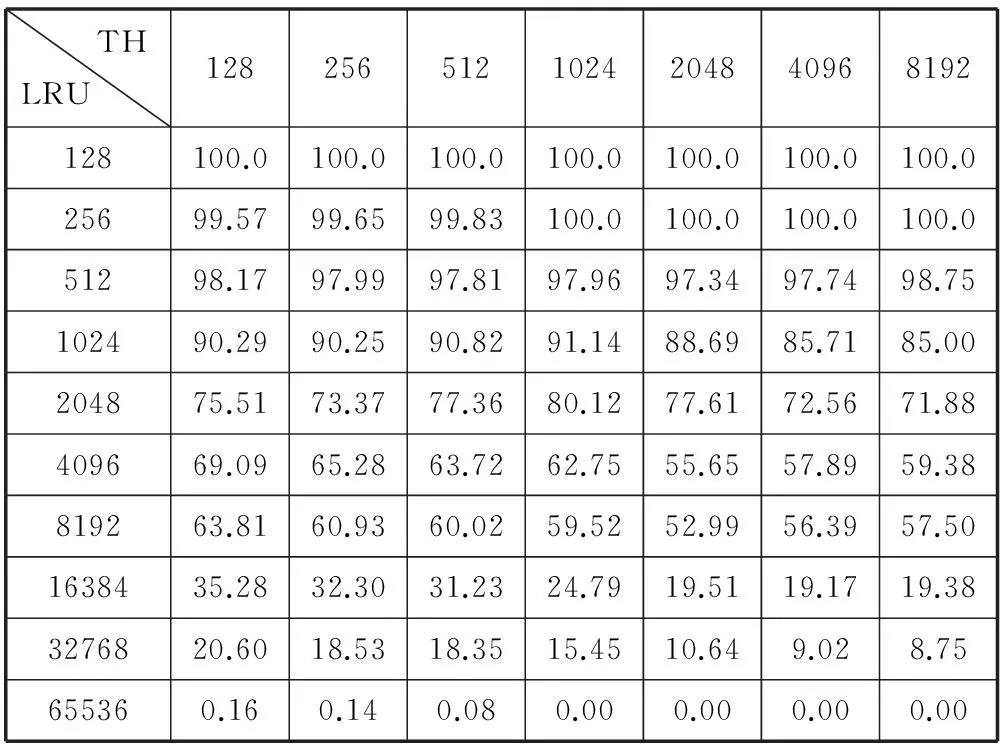
表2 标准LRU算法在LRU缓存变化时测量准确性(误差)

表3 LRU_BF算法在LRU缓存变化时测量准确性(误差)

表1-表3的测量结果可以看出，当三种算法的LRU缓存空间较小时(128时)，由于流数量巨大，而LRU缓存空间太小，导致绝大部分的大流信息被淘汰，测量准确性较差。当LRU缓存增加时，测量的准确性也随之提高，当LRU缓存足够大时，总是能将大流完全检测出来。但本文提出的基于流抽样的LRU算法的收敛速度远快于标准的LRU算法，也优于LRU_BF算法，在使用相同的缓存空间条件下，测量的各种长度阈值的大流的准确性均比标准LRU算法和LRU_BF算法准确。

图5显示以测量长流阈值TH=4096为例(测量其他长流阈值与此类似)，LRU_Sample算法与LRU_BF算法及标准LRU算法，在使用相同的哈希函数和个数以及LRU缓存空间情况下测量准确性的比较。

图5 三种算法在LRU缓存变化时测量长流阈值TH=4096准确性

实验仿真结果表明，相对标准LRU算法和LRU_BF算法，本文提出的LRU_Sample算法具有较高的测量准确性。尤其当LRU缓存空间相对较小时，LRU_Sample算法优势更加明显。这是由于当LRU缓存较小时，标准LRU算法和LRU_BF算法由于缓存空间已满，新到达的大量小流会将LRU缓存中的未识别大流信息淘汰掉。而LRU_Sample算法通过流抽样机制，可以将大部分的小流过滤掉，同时保留已识别的大流信息，减少小流对大流的影响，从而减少算法的测量误差。

4 结 语

由于网络的高速化和大规模化，在线完全测量网络流信息变得越来越难[15]。而“抓大放小”的测量策略可以有效降低算法对计算资源的需求，较准确地测量大流的信息，满足特定网络应用的需求。

本文根据传统LRU算法由于突发性大量小流导致淘汰大流的测量缺陷和网络重尾分布的特点，提出基于流抽样和LRU的大流检测算法。通过采用流抽样机制，可以过滤掉大部分的小流信息，减少小流进入LRU缓存空间的概率，而大流由于长度较长，其所属的报文更容易被抽取。一旦大流的某个报文被抽取到，其后续的报文都将被抽取，这样实现“抓大放小”的策略。分析了算法的复杂度和误判率，并通过试验数据验证算法的有效性。结果表明，与标准的LRU算法和LRU_BF算法相比，新算法可以在使用较少的存储空间的条件下，及时、准确地识别网络中的大流信息，满足实际测量需要。

[1] 周爱平,程光,郭晓军.高速网络流量测量方法[J].软件学报,2014,25(1):135-153.

[2] Tatsuya M,Masato U,Ryoichi K.Identifying elephant flows through periodically sampled packets[C]//Proc of ACM SIGCOMM/IMC’04.Taormina:ACM Press,2004:115-120.

[3] 吴桦,龚俭,杨望.一种基于双重Counting Bloom Filter的长流识别算法[J].软件学报,2010,21(5):1115-1126.

[4] Cristian Estan,George Varghese.New directions in traffic measurement and accounting[J].ACM Transactions on Computer Systems,2003,21(3):270-313.

[5] Duffield N G,Lund C,Thorup M.Estimating flow distributions from sampled flow statistics[C]//Proc of the ACM SIGCOMM Conference on Applications,Technologies 2003,Architectures.Karlsruhe:ACM Press,2003:325-336.

[6] 程光,唐永宁.基于近似方法的抽样报文流数估计算法[J].软件学报,2013,24(2):255-265.

[7] Kim S I,Reddy N A L.Identifying long-term high-bandwidth flows at a router[C]//Proceedings of the 8th International Conference on High Performance Computing.Hyderabad,India,2001:361-371.

[8] 张震,王斌强,张风雨,等.基于LRU-BF策略的网络流量测量算法[J].通信学报,2013,34(1):111-120.

[9] 王风宇,郭山清,李亮雄,等.一种高效率的大流提取方法[J].计算机研究与发展,2013,50(4):731-740.

[10] 王宏,龚正虎.Hits和Holds:识别大象流的两种算法[J].软件学报,2010,21(6):1391-1403.

[11] 王风宇,云晓春,王晓峰,等.高速网络监控中大流量对象的提取[J].软件学报,2007,18(12):3060-3070.

[12] 任高明,夏靖波,乔向东,等.基于LRU淘汰机制的自适应大流检测算法[J].吉林大学学报：工学版,2014,44(4):1159-1164.

[13] 王洪波,裴育杰,林宇,等.基于LRU的大流检测算法[J].电子与信息学报,2007,29(10):2487-2492.

[14] 裴育杰,王洪波,程时端.基于两级LRU机制的大流检测算法[J].电子学报,2009,37(4):684-691.

[15] 张玉,方滨兴,张永铮.高速网络监控中大流量对象的识别[J].中国科学,2010,40(2):340-355.

ELEPHANT FLOW DETECTION ALGORITHM FOR HIGH SPEED NETWORKS BASED ON FLOW SAMPLING AND LRU

Bai Lei1Tian Liqin1Chen Chao1,2

1(SchoolofComputerScience,NorthChinaInstituteofScienceandTechnology,Beijing101601,China)2(SchoolofMechanicalEngineering,ZhejiangUniversity,Hangzhou310058,Zhejiang,China)

In high-speed backbone network, with the increasing speed of network link and the augment in network flow numbers, it becomes a hot issue in current network flow measurement that how to detect the elephant flow information in networks timely and accurately. According to the measurement defect of traditional LRU algorithm that the elephant flows be discarded due to bursting large numbers of mice flows and the feature of heavy tail distribution of network, we proposed a new algorithm for identifying elephant flows—an elephant flow detection algorithm based on flow sampling and LRU. The algorithm filtrates most of the mice flows by flow sampling technology, and identifies elephant flows by LRU algorithm. It separates the filtration and recognition processes, reduces the possibility of mice flows phasing out elephant flows incorrectly, and improves measurement accuracy. We analysed the complexity and missing rate of the algorithm, and analysed the influence of algorithm’s parameter configuration on accuracy of elephant flows measurement through practical test data. Theoretical analysis and simulation result indicated that compare with standard LRU algorithm and LRU_BF algorithm, when the memory spaces used were the same, our algorithm had higher measurement accuracy and practicality.

Network measurement Elephant flow Sampling Hash Least recently used (LRU)

2014-11-25。国家重点基础研究发展计划专项(2011 CB311809)；国家自然科学基金项目(61472137)；中央高校基本科研业务费项目(3142014085)。白磊，讲师，主研领域：网络测量。田立勤，教授。陈超，副教授。

TP393.4

A

10.3969/j.issn.1000-386x.2016.04.027