基于改进MC算法的脑图谱三维重建

朱 恺 樊令仲 李海芳*

基于改进MC算法的脑图谱三维重建

朱 恺1樊令仲2,3李海芳1*

1(太原理工大学计算机科学与技术学院 山西 太原 030024)

2(中国科学院自动化研究所脑网络组研究中心 北京 100190)

3(中国科学院自动化研究所模式识别国家重点实验室 北京 100190)

随着脑图谱在神经外科手术的教学与应用中起到越来越重要的作用，脑图谱的三维重建成为了脑图谱研究的一个主要方向。针对MarchingCubes算法在提取脑图谱数据等值面效率低下的问题，通过对MarchingCubes算法的遍历方法和拓扑结构的研究，提出一种适用于脑图谱三维重建的改进算法，采用该改进算法实现脑图谱三维重建系统。并以Brainnetome Atlas脑图谱数据作为实验数据对系统效率进行测试，实验结果表明，相对于原始算法，改进算法确实提高了三维重建系统处理脑图谱数据的效率。

等值面 MarchingCubes 三维重建 脑分区图谱

0 引 言

脑图谱不仅是临床神经外科手术中的重要工具，而且在神经解剖的教育教学中也扮演着重要的角色。早期的脑图谱均为纸质印刷的二维图像。近年来，随着大脑图谱研究的不断发展，人们开始寻求将脑图谱进行数字化处理，并且从二维图谱逐渐的向三维图谱发展。通过将二维的脑部切片在计算机中重新整合并最终完成脑部结构的三维重建，从而使人们不仅仅能够观察大脑的不同断面也能够以三维的形式对脑结构进行观察。

在脑图谱的三维重建系统中最关键的技术就是体数据的三维重建技术，体数据的三维重建算法直接决定了整个系统的重建效率以及重建准确率。医学体数据三维可视化方法分为两大类[1]：面绘制方法和体绘制方法。面绘制计算量小，处理速度快；体绘制能良好地保持医学图像的细节，但是计算量比较大。因此针对于应用背景选择一种合适的算法就成为了三维脑图谱绘制的一个核心问题。

基于对传统体数据三维重建算法的分析，本文提出一种基于移动立方体算法的快速体数据三维重建算法，提高了三维重建的速度，并应用于三维脑图谱绘制系统当中。

1 三维重建算法

1.1 重建算法的选择

三维重建算法主要分为体绘制和面绘制两种，其中体绘制的常用算法中有很多基于光线投射算法[2]。例如等值面光线投射绘制、最大密度投影算法和合成体法光线投射算法。面绘制算法常用的有Marching Cubes算法。为了提高系统的运行效率就必须选择一种合适的算法对脑图谱数据进行三维重建。为此本文选择了在脑图谱三维重建中经常用到的几种文件规模对以上这些算法的效率进行了测试，测试所用文件列表如表1所示。

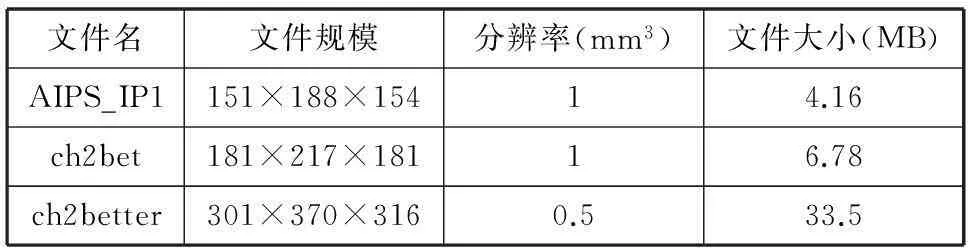
表1 测试文件列表

以上这三个文件中AIPS_IP1为单一脑区数据文件，cpbet为本文中使用的脑模板文件，cpbetter则为一种更为精细的脑模板文件，该文件并没有在本文中使用，这里作为一种极端情况来测试算法效率。

算法效率测试不对原始数据文件进行二次抽样，也不对生成的图形进行优化。测试包含三个指标：(1) 数据处理的时间；(2) 处理完成后图形渲染显示的时间；(3) 所用时间的综合。测试结果如表2所示。

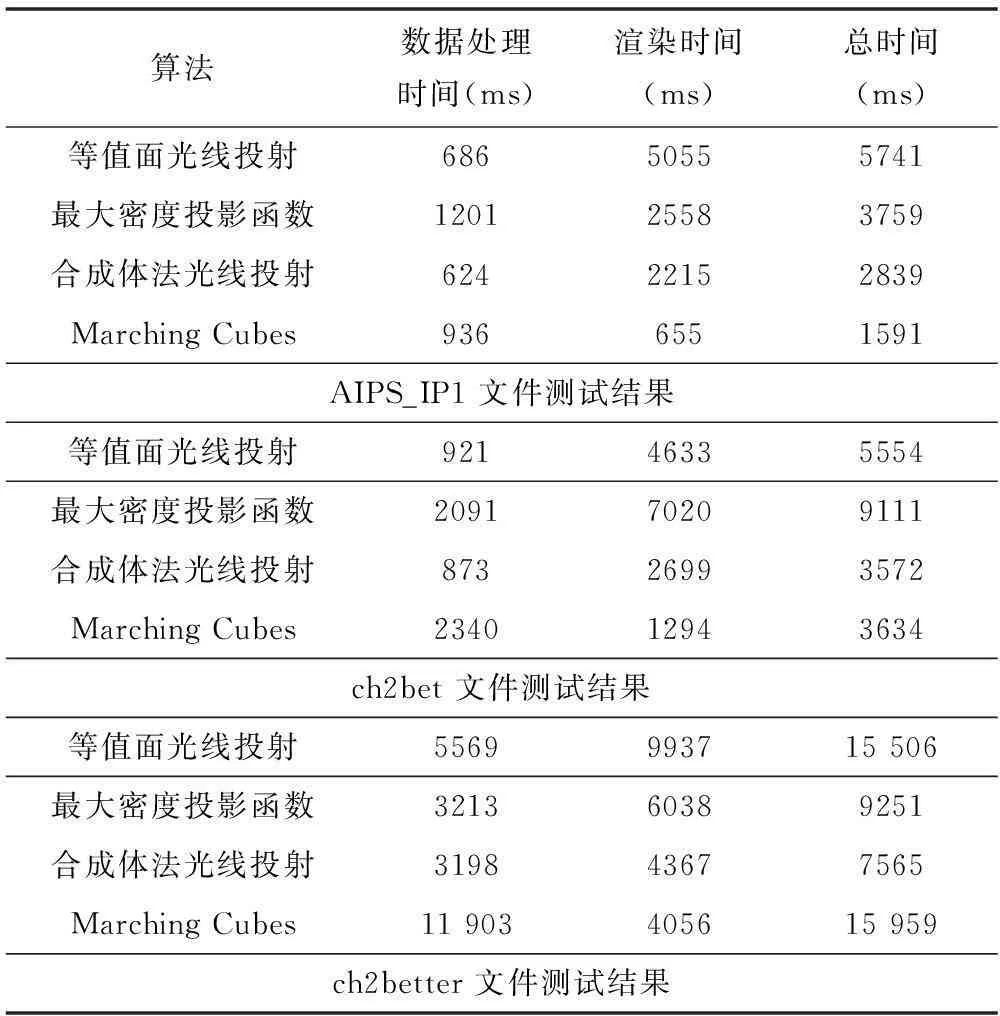
表2 算法效率测试结果

通过表2我们可以看出在这些三维重建算法中，体绘制算法中的合成体法光线投射算法效果是最好的，但是其渲染效率却没有Marching Cubes算法高。在本文中用户对生成的三维图像每进行一次交互操作，都要进行一次渲染，因此渲染时间的长短是算法是否适合本系统的一个重要指标，过长的渲染时间将极大地影响用户的体验。此外体绘制在用户进行视角变换操作时也要进行重新绘制，这大大影响了使用效果。对于移动立方体算法只要提高数据处理的效率就能使其整体效率达到最高。因此本文最后选用Marching Cubes作为系统的三维重建算法。

1.2 MC算法

Lorensond等人于1987年提出的Marching Cubes算法是一种流行的从体数据中提取等值面的算法[3]。其原理是通过对体数据中各个体素进行处理，找到含有等值面的体素并将这些体素中的等值面对应到一系列等值面穿过体素所在立方体的模式中。然后将这些对应好的模式以某种拓扑结构连接成三角面片得到等值面。体素中等值面的模式经过反转、旋转等操作后有很多模式是重复的，去除重复的模式最终体素含有的等值面有15种模式，如图1所示。在此图中深色的顶点代表体素中该顶点处于等值面的阀值之下，也就是等值面在该点之上。根据立方体8个顶点不同的状态决定了该体素中等值面所处的状态。

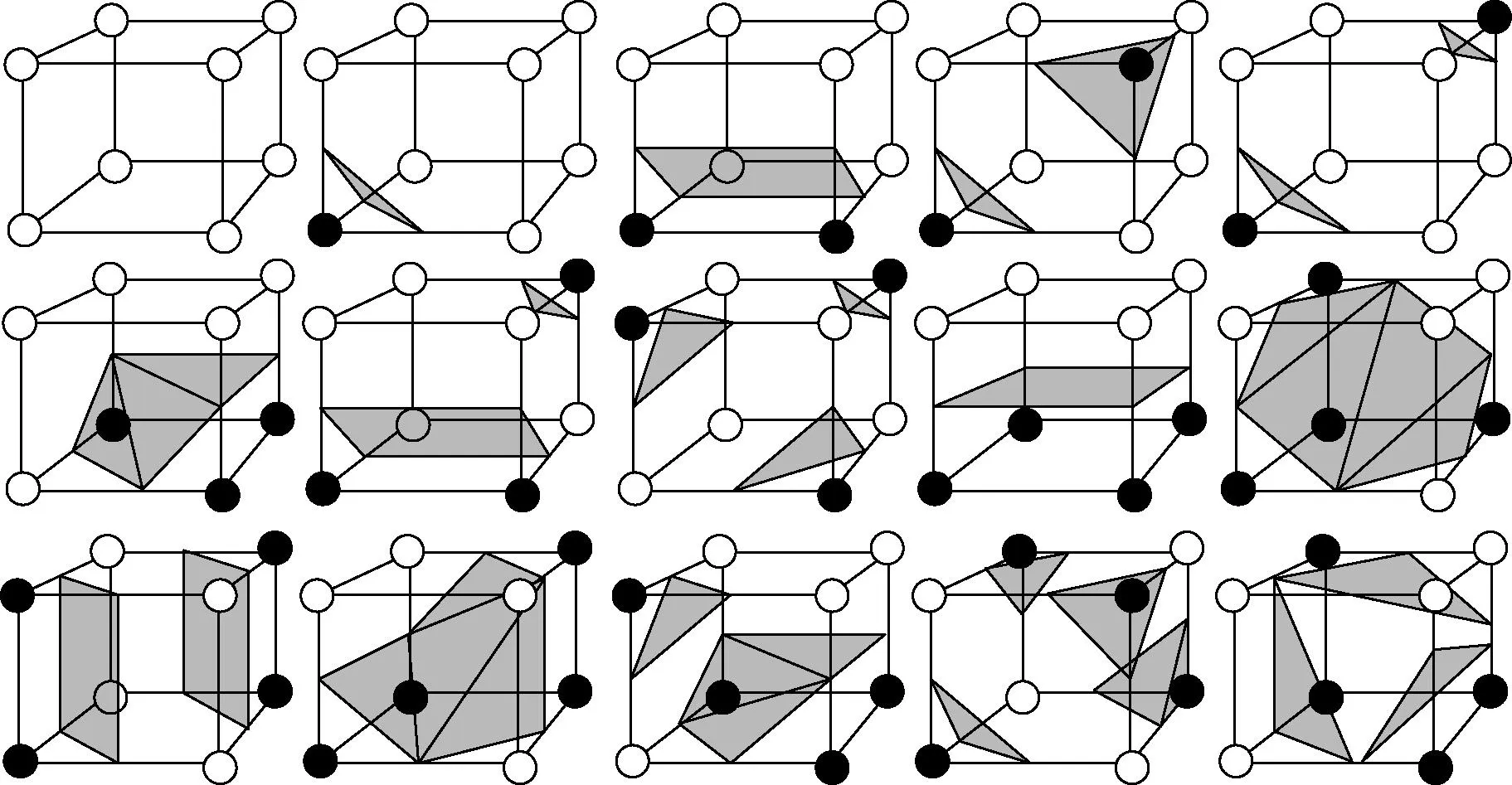
图1 等值面在立方体中的15种模式

得到等值面在体素内的状态后，就要根据等值面状态来得到等值面与体素立方体各条棱相交的顶点，假设有一条棱与等值面相交于点c(x,y,z)，等值面阈值为T。该棱的两个顶点分别为a(x,y,z)和b(x,y,z)，两点的值分别为va与vb，那么交点c的位置可以由下式求出：

(1)

由此类推能将其他交点顶点的位置求出，计算出等值面各个顶点之后，还要计算等值面每个三角面片的法向量，为了计算该法向量就要先计算体素立方体顶点的梯度值，假设顶点梯度值为G(i,j,k)，则梯度值能够由下式求出：

(2)

其中D(i,j,k)为k层(i,j)点的灰度值，在本文应用背景下其实D就可以取为脑图谱数据k层(i,j)点的值，而△x、△y、△z则分别取为xyz方向上的扫描间隔。

MC算法作为一种经典算法本身也存在一些缺点，例如等值面存在二义性、绘制精度不高、处理效率不高等。针对这些缺点Nielson等提出了解决二义性的方法[4]；Lopes提出了提高绘制精度的方法[5]；张迎平等提出的区间树硬件加速索引的方法[6]，通过使用GPU提高了MC算法的处理效率；王旭等初提出的最近邻移动立方体方法[7]则通过建立等分点避免了大量的插值计算；熊邦书等提出的基于连通性的快速曲面重建算法[8]则通过减少遍历体素的个数来提高算法的处理效率。

1.3 MC算法的改进

传统的MC算法是通过对体数据所形成的体素进行逐个遍历来生成小立方体内的等值面，并最终合称为体数据的表面。但是体数据中大多数体素并不与体数据的等值面相交，因此对体素进行逐个遍历将浪费很多时间在空的体素处理上。脑图谱的脑区都是一组体数据中的小部分数据，传统的MC算法在处理脑图谱数据时重建一个较小的脑区也要遍历庞大的体数据的每个体素。但是脑区表面只占整体数据的很小一部分，这使得传统MC算法在重建脑图谱数据时效率比一般的数据下降更为严重。为了解决这种问题我们提出了一种基于体素立方体顶点监测的改进算法。本算法不采用遍历的方式生成等值面，而是判断出种子体素相邻的体素中哪些体素中包含了等值面，再通过区域增长法将包含有等值面的体素全部提取出来进行等值面的绘制。

改进算法的核心在于对种子体素相邻的体素中包含等值面体素的监测。我们通过对体素构成的立方体8个顶点的监测来判断与该体素接邻的体素是否包含等值面。体素构成的立方体包含有8个顶点6个面，每个面包含4个顶点，在属于同一个面的4个顶点中只要这四个顶点不同时大于或小于等值面阈值，则与种子体素共同包含该面的体素也包含有等值面。例如图2所示左右两个体素均包含同一个面，线段ab为该面与左边的体素立方体中等值面的交线，因为该面同属于右面的体素，所以在右面体素中的等值面也必然与此面相交于该交线。由此证明在右面的体素中也是含有等值面的。

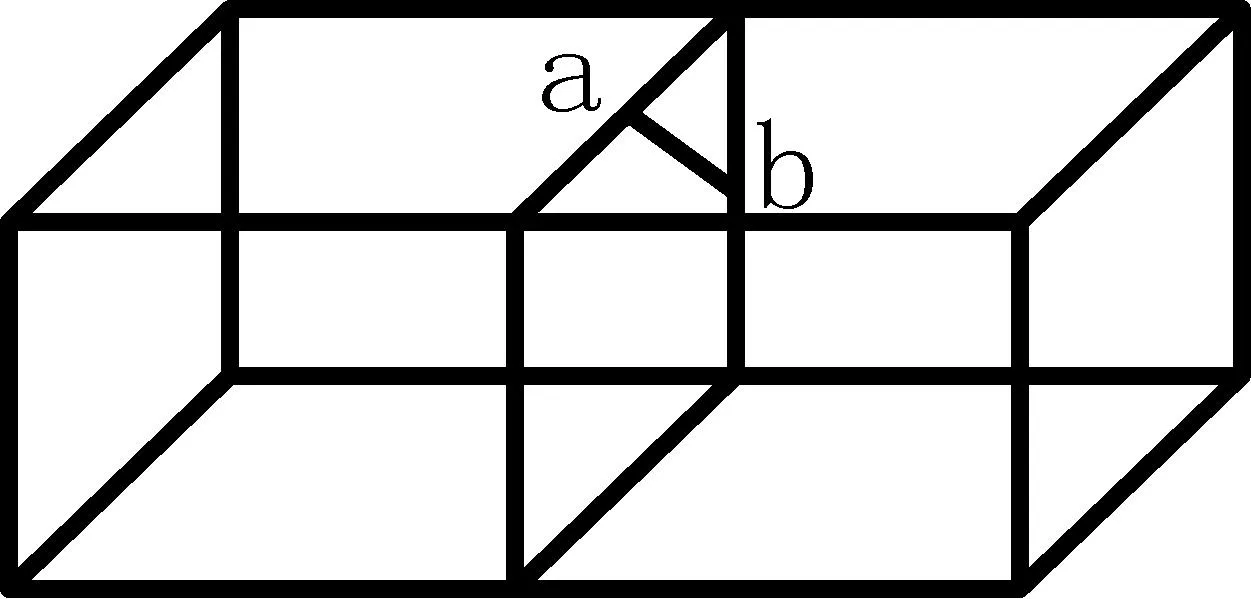
图2 包含有共同面的两个体素立方体

而体素立方体各个面上有没有与体素内等值面的交线通过检测该面的四个顶点就可以确定。四个顶点中我们假设它们都有两种状态即高于阈值和低于阈值状态，则一个面有1个点处于不同状态，2个点处于不同状态，和全部处于同一状态三种情况。其中1点状态不同有一种交线形式，2点有两种，全部处于同一状态则没有交线出现，如图3所示。综上所述通过对种子体素立方体一个方向的面的四个顶点进行监测就可以判断这个方向的接邻体素是否含有等值面。

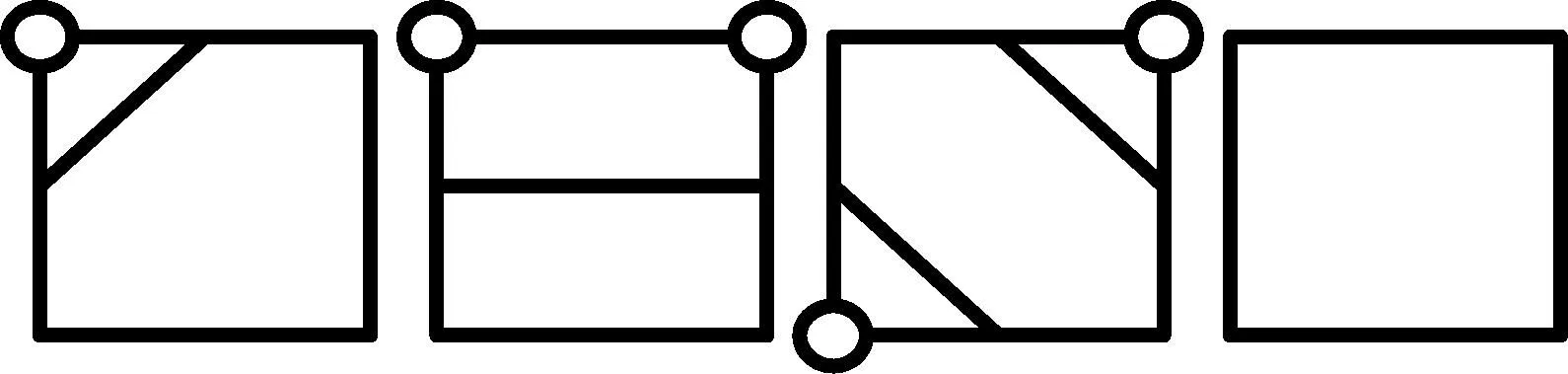
图3 体素内等值面与体素表面相交的几种情况

通过上面的规则，只要给出相应的种子体素我们就能够将整个体数据中包含有等值面的体素提取出来进行处理，避免将体素逐个遍历从而节省大量时间。

1.4 改进算法的实现

实现该算法首先要解决的问题是种子体素的选取问题，我们采用了二次取样的方法进行种子点的提取，即遍历时对每个维度增长速度进行加倍。这样能够提高遍历的速度，一般二次取样都会降低体数据的精度，但是本算法二次取样后得到的体素在进行区域增长获取边界体素后并不会影响精度。在获得了种子体素后就可以进行邻接体素的检测了，本算法使用了一个栈和一个哈希表来辅助算法计算。

算法流程为：

(1) 将种子体素入栈，监测接邻体素8个顶点，判断哪些接邻体素具有等值面，将具有等值面的接邻体素入栈，并加入哈希表。

(2) 监测栈是否为空，为空则算法结束，不为空则将栈顶部的体素弹出。

(3) 将弹出体素的八个顶点进行监测，判断哪些接邻体素据有等值面，监测具有等值面的接邻体素是否在哈希表中，不在表中的接邻体素入栈。

(4) 为弹出的体素进行等值面绘制，转到第(2)步。

算法核心编程：

//算法通过栈和哈希表提取含有等值面的体素立方体

while (!readyCubes.empty())

{

idx=readyCubes.top();

readyCubes.pop();

//从图谱数据文件取出组成一个立方体8个顶点的值

s[0] = scalars[idx];

s[1] = scalars[idx+1];

s[2] = scalars[idx+1 + dims[0]];

s[3] = scalars[idx + dims[0]];

s[4] = scalars[idx + sliceSize];

s[5] = scalars[idx+1 + sliceSize];

s[6] = scalars[idx+1 + dims[0] + sliceSize];

s[7] = scalars[idx + dims[0] + sliceSize];

//向栈加入邻接立方体，并为当前立方体添加哈希标记

//监测上方邻接立方体在哈希表中是否有记录以及是否有等值

//面，如果有等值面且哈希表无记录则将其入栈

if (!(s[0] < min && s[1] < min && s[2] < min && s[3] < min||s[0] > max && s[1] > max && s[2] > max && s[3] > max))

{

if((idx-sliceSize)<0)

continue;

if (!CheckedCubes.find(idx-sliceSize))

{

readyCubes.push(idx-sliceSize);

CheckedCubes.insert(idx-sliceSize);

}

}

//监测下方邻接立方体在哈希表中是否有记录以及是否有等值

//面，如果有等值面且哈希表无记录则将其入栈

if (!(s[4] < min && s[5] < min && s[6] < min && s[7] < min||s[4] > max && s[5] > max && s[6] > max && s[7] > max))

{

if((idx+sliceSize)<0)

continue;

if (!CheckedCubes.find(idx+sliceSize))

{

readyCubes.push(idx+sliceSize);

CheckedCubes.insert(idx+sliceSize);

}

}

//监测左方邻接立方体在哈希表中是否有记录以及是否有等值

//面，如果有等值面且哈希表无记录则将其入栈

if (!(s[0] < min && s[3] < min && s[4] < min && s[7] < min||s[0] > max && s[3] > max && s[4] > max && s[7] > max))

{

⋮

}

//监测右方邻接立方体在哈希表中是否有记录以及是否有等值

//面，如果有等值面且哈希表无记录则将其入栈

⋮

//监测前方……

⋮

//监测后方……

⋮

}

2 VTK应用

2.1 VTK简介

VTK(visualization toolkit)[9,10]是一个开源的免费软件系统，我们可以直接从官网上获得最新版本。它广泛应用于三维计算机图形学、图像处理和可视化。VTK具有强大的三维图形功能，在支持体绘制的同时也保留了传统的面绘制。其独特的数据管道化处理使得VTK在处理大量数据时不用考虑内存资源的限制。它将我们在可视化开发中常用的一些算法封装起来，提供给我们相关的类，通过将开发中的细节屏蔽起来大大简化了可视化开发中的复杂程度。此外VTK还能够跨平台并且支持数据并行处理，它能够在任何Unix和Windows平台上使用，而且具有良好的可移植性。

2.2 VTK可视化管线

VTK对数据进行可视化采用的是独特的管线处理机制[11]，通过管线机制VTK能够读取数据、对数据进行处理、将处理后的数据传入渲染引擎进行显示。这种机制减小了编程的复杂度，使数据的输入与数据的处理过程相分离。将数据与处理算法引入后只需要保证输入与处理过程的接口一致就可以了，而不用去考虑除了管线以外其他的因素。并且在对同一数据用不同的算法进行处理时，只需要更换相关处理过程的类就可以了。

处理管线一般包括数据源、过滤器、映射器、表演者、渲染器和窗口。另外用户接口和控制器虽然不是处理管线中必要的部分，但是作为应用程序用户交互一部分也是十分重要的。处理管线根据数据类型的不同具有不同的数据处理过程，但是其本质是相同的，流程如图4所示。

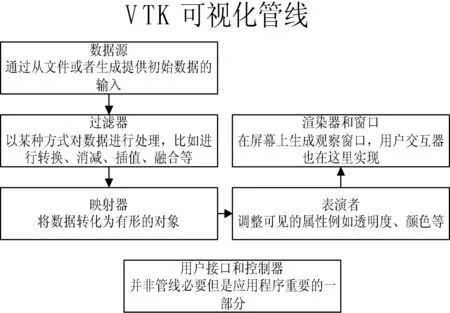
图4 VTK可视化处理管线

改进算法融入到VTK可视化管线的方法如下：

(1) 读入脑图谱数据

vtkImageReader *imreader = vtkImageReader::New();

GetImageReader(imreader);

(2) 建立数据处理过滤器，并将改进算法引入其中

//其中MarchingCubesReduce为改进MC算法的封装类

MarchingCubesReduce *extractor = MarchingCubesReduce::New();

extractor->SetInputConnection(imreader->GetOutputPort());

extractor->SetValue(0,3);

extractor->Update();

(3) 建立映射器

vtkPolyDataMapper *mapper = vtkPolyDataMapper::New();

mapper->SetInputConnection(extractor->GetOutputPort());

mapper->SetColorModeToMapScalars();

mapper->SetScalarRange(1.0,20.0);

(5) 添加表演者、渲染窗口以及控制器

vtkActor *actor = vtkActor::New();

actor->GetProperty()->SetColor(0.5,0.0,0.0);

actor->SetMapper(mapper);

vtkRenderer *ren = vtkRenderer::New();

vtkRenderWindow *renWin = vtkRenderWindow::New();

renWin->AddRenderer(ren);

vtkRenderWindowInteractor *iren = vtkRenderWindowInteractor::New();

iren->SetRenderWindow(renWin);

在引入改进MC算法之后，该算法能够提高过滤器处理脑图谱数据的效率。

2.3 生成图像性能及质量的优化

考虑到系统最后的运行效果，我们要对三维重建后得到的图形进行优化，减小它的复杂度、提高显示效果，加快系统的运行速度。对生成图像进行优化主要从三方面入手：对原始数据进行精简；选择产生更简单图形的算法；对最终生成图像采用优化算法。

VTK类库中有多种方法能对原始数据进行简化，缩小原始数据的规模。其中vtkImageResample类通过线性插值方式对输入的数据进行重新采样，重新采样的结果可以更致密或者相对稀疏一些。通过该类我们能够将原始数据的质量降低，从而降低数据的复杂程度，提高处理速度。另外VTK中的vtkImageShrink3D类能够实现二次抽样，可以加速数据的输入。通过该类的相关函数能够控制抽样的精度从而得到速度和质量平衡的效果。该类搭配vtkImageResample类能够大幅度地提高数据的处理速度。

选择性能更优良的处理算法能够使最后获得的图像有更好的效果，并提高处理速度。本文使用了MC算法计算脑图谱数据的等值面，该算法得到的最后结果经过优化与未经过优化的结果相比其最后图像所包含的三角面片大大减少。如图5所示。优化前脑区三维重建包含25 296个单元，优化后包含15 412个单元。

图5 三维重建优化前后比较

如果对最后生成的图像面片数量还是不满意还可以通过使用VTK提供的vtkDecimatePro 类，它能够有效地减少生成图像的三角面片。不过削减比例过大有可能破坏图形原本的拓扑结构。

对图形进行削减后虽然提高了性能但是有可能使图像变得参差不齐，这时我们可以通过图像平滑类vtkSmoothPoly-DataFilter对图像进行处理，提高其显示质量。该类通过对生成图像各个点的坐标进行修改，从而使构成图形的网格更疏松，各个定点的分布更加均匀，最终使图形的各个单元获得更好的形状。

优化图像步骤如下：

(1) 重新采样缩小数据规模

vtkImageResample *irreduce =vtkImageResample::New();

Irreduce->SetInput(imreader.GetOutput());

Irreduce->SetAxisMagnificationFactor(0, 0.5);

Irreduce->SetAxisMagnificationFactor(1, 0.5);

Irreduce->SetAxisMagnificationFactor(2, 0.5)

(3) 使用vtkDecimatePro 类削减面片

vtkDecimatePro *DecimatePro = vtkDecimatePro::New();

DecimatePro->SetInputConnection(extractor->GetOutputPort() );

DecimatePro->SetTargetReduction(0.3);

DecimatePro->PreserveTopologyOn();

(3) 对生成的图像进行平滑处理

vtkSmoothPolyDataFilter *smoother = vtkSmoothPolyDataFilter::New();

smoother->SetlnputConnection(DecimatePro->GetOutput());

smoother->SetNumberOflterations(200);

(4) 计算面片的法向量

vtkPolyDataNormals *Normals = vtkPolyDataNormals::New();

Normals->SetInputConnection(smoother->GetOutputPort());

Normals->FlipNormalsOn();

3 系统结构及人机界面

3.1 系统结构设计

本文制作的脑图谱三维重建系统基于VTK以及在医学图像处理平台3D Slicer 开发中曾用到的KWWidgets[12]类库。通过人机交互界面控制脑图谱数据的输入，以及脑图谱数据的处理。根据不同的显示要求对数据处理调用相应的算法和优化处理过程，最终为脑图谱的三维显示、二维显示、脑图谱各个脑区的侦测和标记提供处理好的数据。系统结构如图6所示。

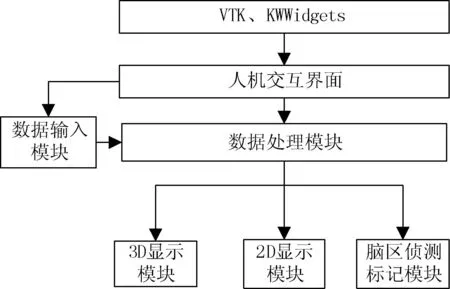
图6 系统结构设计图

3.2 人机交互界面设计

系统图形界面使用KWWidgets界面库制作，该类库也是由VTK的开发公司开发的。因此与VTK库能良好的配合使用，同时这套类库提供了很多可视化编程要用到的控件，能极大地节省软件开发的时间，此类库还支持TCL/TK脚本语言，方便进行开发。

整个系统的用户界面分为三部分：(1) 主控制面板；(2) 主显示窗口；(3) 二维图像显示窗口。如图7所示。

图7 系统界面

(1) 主控面板包含有相关文件的输入输出功能，为各个脑区建立标签的功能，调整脑区三维图形光照的功能，以及调整脑区三维图形的颜色与透明度的功能。

(2) 主显示窗口用来显示脑图谱的三维重建图像，用户可以通过鼠标点击拖拽和滚轮滚动控制三维图像的角度变换，以及视角的拉近和推远。

(3) 二维图像显示窗口显示二维的脑图谱数据，用户可以在任意一个显示窗口点击，从而交互的改变其他窗口显示的脑切面的位置。

4 实验及结果分析

4.1 实验数据介绍

本系统要求的输入文件为包含脑图谱数据的NIfTI[13]格式文件。在本文中的实验数据为来自于中国科学院自动化研究所脑网络组研究中心的脑网络组图谱(Brainnetome Atlas)中的脑区分区结果[14](http://atlas.brainnetome.org)。文件维度为181×271×181。本图谱文件包含有两个大脑半球的39个脑区，图谱文件各个分区所包含的体素value值都为其所属分区的编号值。如表3所示。

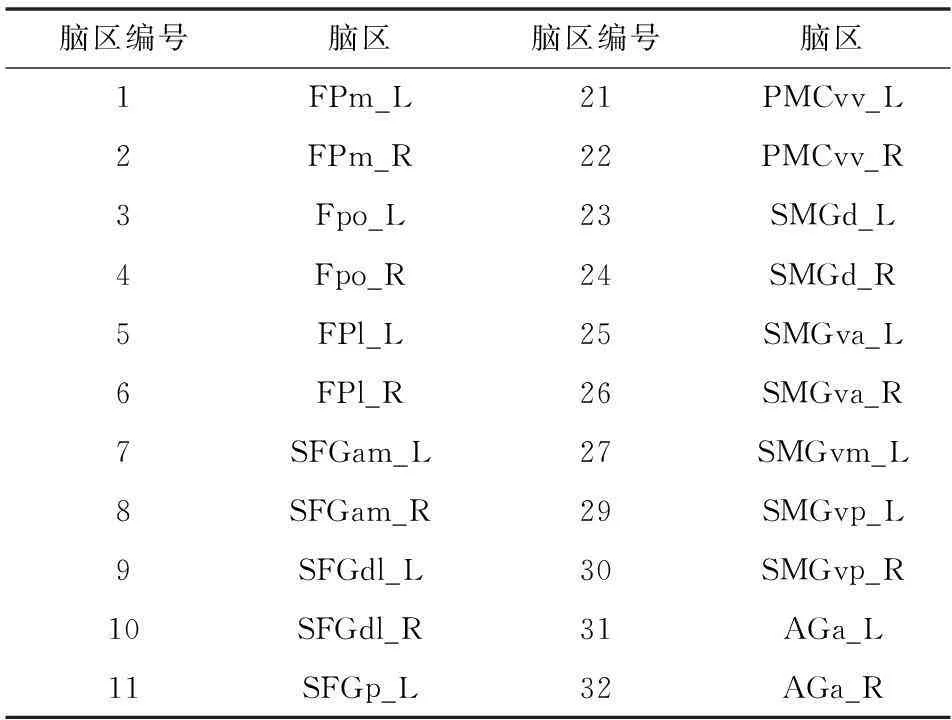
表3 Brainnetome Atlas脑图谱数据

续表3

此外由于实验数据的脑图谱文件不包含脑模板。因此本文在实验中输入文件还包含了与图谱文件匹配的的cpbet脑模板文件，用来形成脑模板的三维图像，使重构后的图谱文件三维图像能够在模板上显示。

4.2 系统效率分析

本系统在CPU为酷睿双核2 GHz，3 GB内存，显卡为GT130m的平台上对实验数据进行处理。实验得到的MC原始算法与改进后的效率对比如表4所示。

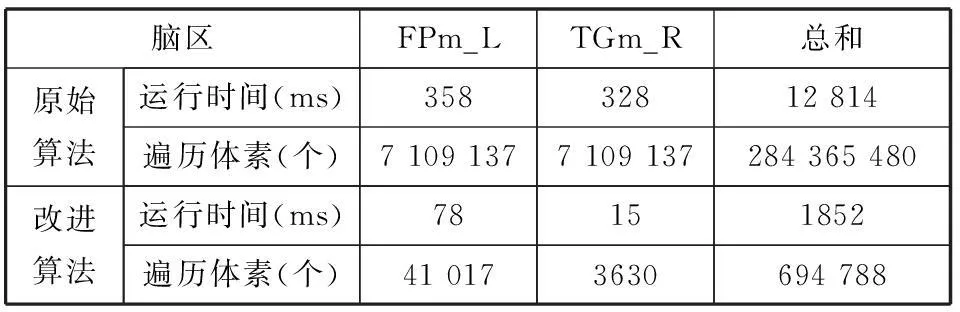
表4 原始算法与改进算法效率对比

从对比数据中可以看出原始MC算法重建整个脑图谱表面比改进算法多进行了400多倍的遍历次数。但是由于栈和哈希表所占用的时间耗费,实际处理时间虽然没有遍历次数下降的幅度大但是也能够从12 814 ms加快到1852 ms，减少了85%的时间耗费。重建时间分为遍历时间和绘制时间。绘制时间是对体素的等值面进行绘制的时间这个时间两种算法基本持平。在遍历时间上改进算法根据重建表面所占的体素数来决定耗费时间，原始算法则遍历整个体数据空间，因此原始算法的遍历时间基本上是不变的,改进算法提高效率就是源于遍历时间相对于原始算法大大减少。图8给出了随着处理体素数量增长两种算法的效率对比。

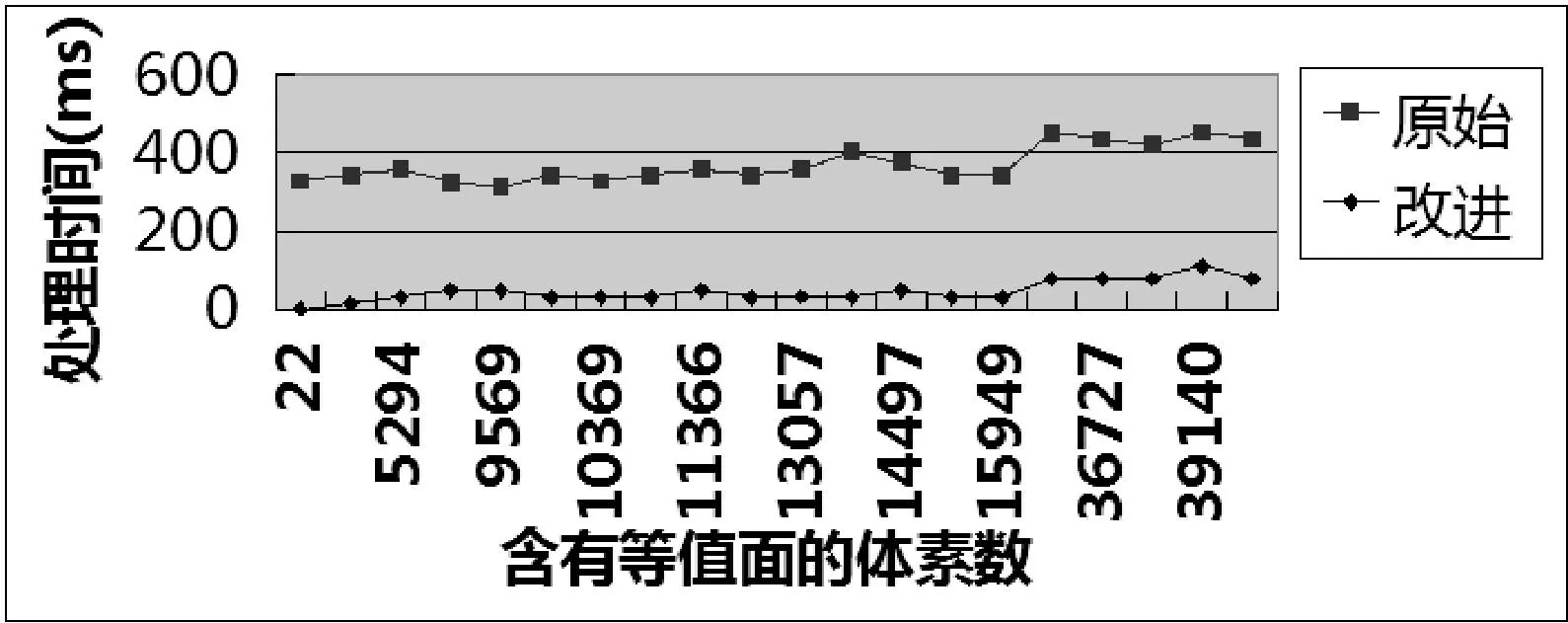
图8 改进算法与原始算法基于体素数的效率对比

4.3 三维重建效果

图9给出了两种算法重建的单个脑区图形，改进算法与原始算法产生的图形相差无几。证明使用改进算法进行加速不会影响重建效果。图10则给出了二维脑图谱图像与三维重建的对比，其中二维图像为单层图像看不见下层的脑区，三维重建后所有的脑区都能够方便地进行观察。

图9 单个脑区的重建对比

图10 三维重建结果与二维图谱对比

5 结 语

脑图谱一直以来都是研究脑部结构和功能的重要手段。目前，脑图谱相关的研究工作正在国内外脑科学研究单位如火如荼的开展。医学三维重建技术作为一门已经成熟的技术应用在脑图谱三维重构上极大地提升了脑图谱的可视化效果。本文对脑图谱三维重建显示过程中处理算法的选择、图形的优化以及用户交互进行设计，并完成了一个处理速度快、显示质量达到应用要求的脑图谱三维重建和可视化系统。并且使用Brainnetome Atlas的临床数据对系统进行测试，基于改进MC算法的三维重建系统确实在脑图谱数据的处理上展现了高于原始算法的效率。

在本文课题进行过程中，VTK类库得到了大量的应用。它作为一款开源的可视化软件，其功能十分强大，而且可以根据个人需要对其进行改进，这方面是其他软件做不到的。

以上工作只是脑图谱三维重建及可视化的一个初步探索，很多功能还尚待进一步实现。随着对体数据三维重建算法在并行计算和GPU处理等方面改进的实现，我们将进一步丰富该系统的功能，提高其重建效率，改善其可视化效果。

[1] 常旖旎,鲁雯,聂生东.医学图像三维可视化技术及其应用[J].中国医学物理学杂志,2012,29(2):3254-3258.

[2] 解立志,周明全,田沄,等.基于光线投射算法的脑血管体绘制技术[J].系统仿真学报,2012,24(9):1-5.

[3] 陈卿.医学影像三维可视化Marching Cubes算法研究[D].成都:电子科技大学,2011.

[4] Nielson G M.On marching cubes[J].Visualization and Computer Graphics,IEEE Transactions on,2003,9(3):283-297.

[5] Lopes A,Brodlie K.Improving the robustness and accuracy of the marching cubes algorithm for isosurfacing[J].Visualization and Computer Graphics,IEEE Transactions on,2003,9(1):16-29.

[6] 张迎平,高国贤,陆一峰,等.基于区间树硬件加速索引的Marching Cubes算法[J].计算机辅助设计与图形学学报,2012,24(7):871-878.

[7] 王旭初,王赞.基于最近邻Marching Cubes的医学图像三维重建[J].计算机工程与应用,2012,48(18):154-158.

[8] 熊邦书,何明一,俞华璟.基于空间连通性的快速曲面重建算法[J].系统仿真学报,2005,17(1):75-78.

[9] 洪涛,潘志方,林立本,等.VTK医学图像三维重建应用及实现[J].计算机系统应用,2011,20(4):127-130.

[10] Sun S,He J,Ma L.3D visualization system for medical image based on VTK and OK Series Image Board[C]//Computer Science and Service System (CSSS),2011 International Conference on.IEEE,2011:951-954.

[11] Caban J J,Joshi A,Nagy P.Rapid development of medical imaging tools with open-source libraries[J].Journal of digital imaging,2007,20(1):83-93.

[12] Fang L,Wan Z,Zeng W,et al.Research on Internationalization of 3D Slicer[C]//Computer Sciences and Applications (CSA),2013 International Conference on.IEEE,2013:469-473.

[13] Larobina M,Murino L.Medical Image File Formats[J].Journal of digital imaging,2014,27(2):200-206.

[14] Jiang T,Zhou Y,Liu B,et al.Brainnetome-wide association studies in schizophrenia:The advances and future[J].Neuroscience & Biobehavioral Reviews,2013,37(10):2818-2835.

3D RECONSTRUCTION OF BRAIN ATLAS BASED ON MODIFIED MARCHING CUBES ALGORITHM

Zhu Kai1Fan Lingzhong2,3Li Haifang1*

1(SchoolofComputerScienceandTechnology,TaiyuanUniversityofTechnology,Taiyuan030024,Shanxi,China)2(BrainnetomeCenter,InstituteofAutomation,ChineseAcademyofSciences,Beijing100190,China)3(NationalLaboratoryofPatternRecognition,InstituteofAutomation,ChineseAcademyofSciences,Beijing100190,China)

Along with that brain atlas plays more and more important role in teaching and application of neurosurgery operation, 3D reconstruction of brain atlas has become a major research direction of brain atlas. In order to improve the efficiency of MarchingCubes algorithm in extracting isosurface of brain atlas data, we propose an improved algorithm suitable for 3D reconstruction of brain atlas through the study on the traversal method and topological structure of MarchingCubes algorithm, and realise the brain atlas 3D reconstruction system based on the improved algorithm. We use brain atlas data of Brainnetome Atlas as the experimental data to test the efficiency of the system, experimental results show that relative to original algorithm the improved algorithm really improves the efficiency of 3D reconstruction system in processing brain atlas data.

Isosurface MarchingCubes 3D reconstruction Brain atlas

2014-09-06。国家自然科学基金项目(61373101)；山西省自然科学(青年科技研究)基金项目(2014021022-5)；山西省科技攻关项目(20130311037-4)。朱恺，硕士生，主研领域：智能信息处理。樊令仲，助理研究员。李海芳，教授。

TP391.7

A

10.3969/j.issn.1000-386x.2016.04.042