基于三角随机模拟的生活垃圾填埋场地下水环境健康风险评价模型
王月,安达*,席北斗,唐军,梁欢欢,2,张伯强,3
1.中国环境科学研究院国家环境保护地下水污染过程模拟与控制重点实验室,北京 100012
2.上海大学环境与化学工程学院,上海 200444
3.东华理工大学水资源与环境工程学院,江西 南昌 330013
基于三角随机模拟的生活垃圾填埋场地下水环境健康风险评价模型
王月1,安达1*,席北斗1,唐军1,梁欢欢1,2,张伯强1,3
1.中国环境科学研究院国家环境保护地下水污染过程模拟与控制重点实验室,北京 100012
2.上海大学环境与化学工程学院,上海 200444
3.东华理工大学水资源与环境工程学院,江西 南昌 330013
基于US EPA健康风险评价方法,将三角模糊数和随机模拟方法进行耦合,建立基于三角随机模拟的地下水环境健康风险评价模型,并以我国北方某生活垃圾填埋场为例,进行地下水环境健康风险评价。结果表明:6口地下水水质监测井的儿童健康风险均超过可接受水平,其中Z1和Z2监测井的风险值均分布于Ⅲ、Ⅳ 2个风险等级;3口监测井的成人健康风险超过可接受水平,其中Z6监测井的风险值分布于Ⅴ、Ⅵ 2个风险等级。与常规确定性方法的评价结果进行对比分析可知,该模型在一定程度上解决了传统确定性评价方法存在的不确定性问题,不仅可以判定地下水污染可能隶属的风险等级,而且可以定量得出其相应的概率水平,可为决策者提供更加精确的环境健康风险评价信息,为地下水污染管理工作提供依据。
三角随机模拟;垃圾填埋场;地下水;健康风险评价
随着城市数量和规模的不断扩大,垃圾填埋场已成为重要的地下水污染源。国内外由于垃圾渗滤液造成的地下水污染事件并不少见[1]:美国7 500个现有垃圾填埋场中,对周边地下水环境已造成明显污染的填埋场占75%;加拿大300个垃圾填埋场中,80%填埋场对周边的地下水环境已产生不同程度和范围的影响;其他发达国家也存在相似状况[2]。在我国,城市垃圾以每年8%~9%的速度增长[3],唐山市、辽宁省、上海市、吉林省等地均发生过垃圾填埋场引起的地下水污染事故[1,4]。
对垃圾填埋场造成的地下水污染进行健康风险评价具有重要意义,可为垃圾填埋场场地污染的治理、地下水源的保护及地下水污染风险管理工作提供科学依据。然而,与国外相比,我国的健康风险评估起步晚,对于风险评价模型的研究比较缺乏[5]。目前普遍采用的健康风险评价方法是1989年由美国国家环境保护局(US EPA)颁布的《超级基金场地健康评价手册》中提出的四步法,即数据收集和数据评估、毒性评估、暴露评估、风险表征[6],是一种确定性评价方法。而在实际运用过程中,不确定性贯穿于健康风险评价的全过程,包括环境系统自身的复杂性,以及理论研究水平的限制,造成评价者对于评价对象及评价系统存在主观认识上的不确定性;评价区域内采样或监测样本的有限性及测量、分析误差的存在,使得模型中参数数据存在较大的模糊性等。因此,环境健康风险评价系统是一个随机性、模糊性等多种不确定性共存的复杂系统。为了降低评价过程中的不确定性,提高评价结论的可靠性,金菊良等[7]将蒙特卡罗(Monte Carlo)随机模拟方法在地表水环境健康风险评价中进行了应用研究。但对于地下水环境系统的健康风险而言,数据获取的难度及精确度要远远难于地表水环境,从而制约了运用随机理论(蒙特卡罗方法)对污染物状态进行模拟分析,不能准确地反映评价区域内真实的污染水平及其分布特征,难以采用随机模型进行模拟分析[8-9]。三角模糊数理论综合考虑了数据的平均值和标准差,能够反映参数浓度在一定置信度水平下的波动范围,在进行地下水环境健康风险评价时,在监测数据资料较少或精确度不高的情况下,可以近似描述参数的正态分布[9],适用于处理和表达模糊信息[10],可以有效降低评价过程中的不确定性。
因此,笔者基于US EPA健康风险评价方法,将三角模糊数和随机模拟方法进行耦合,建立基于三角随机模拟的地下水环境健康风险评价模型,并应用于北方某生活垃圾填埋场地下水环境健康风险评价,确定地下水环境健康风险等级及概率水平,解决评价过程中由于数据资料不丰富等因素带来的不确定性问题,保证评价结论的可靠性,在一定程度上可为垃圾填埋场地下水污染风险防控工作提供依据。
1 研究方法
1.1 地下水环境健康风险评价模型
地下水环境健康风险评价主要针对地下水中对人体有害的物质,根据世界权威机构编制的分类系统,可将地下水中的污染物分为基因毒物质和躯体毒物质,基因毒物质包括化学致癌物和放射性污染物,躯体毒物质则指非致癌化学有毒物质,但一般来讲,地下水中的放射性污染物的含量极低,一般的水质监测,根本检测不出来。人类通过饮用地下水,水中不同污染物所引起的健康风险会不同,其数学模型也不同。
1.1.1 化学致癌物所致健康风险评价模型
化学致癌物所致健康风险评价模型[11-13]为:
Dig=WCiA
(1)
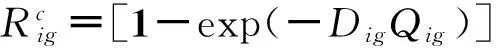
(2)
(3)
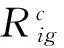
1.1.2 非致癌污染物所致健康风险评价模型
非致癌污染物通过饮水途径导致的平均个人健康风险评价模型为:
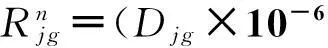
(4)
(5)
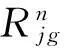
1.1.3 地下水环境健康风险评价总模型
假设地下水中各种污染物对人体健康的影响彼此之间不发生任何关系,即是独立的,其产生的累积效应呈相加关系。可以得到地下水环境总的健康风险:
R总=Rc+Rn
(6)
式中R总为化学致癌物和非致癌污染物所产生健康危害的总和。
1.2 三角随机模拟模型
1.2.1 三角模糊数的定义
三角模糊数是由美国学者Zadeh于1965年提出的模糊集概念[15],其定义如下:
(7)

图1 三角模糊数分布Fig.1 The distribution of triangular fuzzy numbers
为了降低数据的误差,提高数据的可信度,根据数理统计学原理[16],常态分布或近似常态分布的数列,约有95%以上的数据位于平均值的上下2倍标准差之间,该范围内的数据对于原数据序列具有较好的代表性。三角模糊数(a,b,c)根据数据上下限分析原理进行确定[17]:a取数据的均值减去2倍标准差;b取数据的统计平均值;c取数据的均值加上2倍标准差。
1.2.2 三角模糊数的随机模拟
采用Crystal ball®软件进行三角随机模拟,其能够基于用户定义的假设变量概率分布及预测参数,在可能值范围内,通过设定运行参数,产生一系列随机数,得到各预测参数的可能值区间及其相应的概率。由于在数据资料较少或精确度不高的情况下,三角模糊数可以用于近似描述参数的正态分布,因此可以利用Crystal ball®软件中的三角分布类型,在已经构建的三角模糊数基础上,对各参数进行随机模拟,产生一系列符合正态分布的随机数。由于现有三角模糊数的乘法、除法和函数运算等尚不够严谨,实现过程比较复杂[18],因此,通过随机模拟能够将三角模糊数及其函数之间的运算转化为普通实数间的运算,降低运算过程可能产生的误差,并得到能够准确反映预测参数分布特征的统计信息。该方法与金菊良等[7]的三角随机模拟方法最大的不同,在于直接利用Crystal ball®软件中的三角分布类型进行随机模拟,避免了采用逆变换法导致的计算复杂性,以及数据变换过程中可能产生的误差,简化了计算过程,方法较为简单快捷。已有的研究[7,19]表明,蒙特卡罗方法的模拟次数越多,其结果越接近于真实的概率分布,模拟次数一般选取频率分布收敛时所对应的次数。
1.3 基于三角随机模拟的地下水环境健康风险综合评价模型
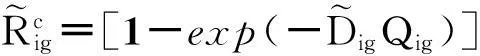
(8)
(9)
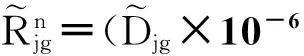
(10)
(11)
(12)
根据前人的研究成果[20],5.0×10-5a-1为最大风险可接受水平,将评价标准区间分为6个等级,其中,随着风险等级的增大,对人类造成的危害逐级增加。对各风险等级进行赋值,如表1所示。

表1 评价标准等级与分值
根据表1以及隶属于各风险等级的概率,得出评价对象的综合风险值。
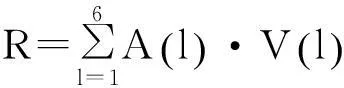
(13)
式中:A(l)为各风险等级的概率水平;V(l)为各等级的分值。
2 实例研究
2.1 区域概况
北方某地区的生活垃圾填埋场属于正规垃圾填埋场,自2007年10月1日开始投产运行,垃圾处理量为150 td,填埋区面积54.11 hm2,填埋深度17 m,填埋容量约190×104m3。
该区域地下水补给主要来源为大气降水;地表沉积物主要为第四纪砂砾卵石和黏性土沉积,厚度在50~60 m;地层岩性主要是由细砂、砾砂组成的第四系潜水,含水层厚达100 m,富水性好,水量丰富,渗透系数高,无弱透水性顶板,该层地下水防护条件较差,潜水极易受地表污染物影响。该区域的地下水流向是西南—东北。
2.2 参数选择
根据生活垃圾填埋场地下水环境中的污染物种类、常规监测项目,以及水体中化学有毒污染物的分类,选取镉(Cd)、砷(As)、氨氮(NH3-N)、挥发酚、汞(Hg)、铅(Pb)、锰(Mn)和氟化物共8种污染物为评价参数,其中,Cd、As为化学致癌物,其致癌强度系数(Qig)分别为6.1和15 〔mg(kg·d)〕-1;NH3-N、挥发酚、Hg、Pb、Mn、氟化物为非致癌污染物,其参考剂量见表2。
表2 非致癌污染物的参考剂量(饮水途径)
Table 2 Reference dose for non-carcinogen by drinking approach mg(kg·d)
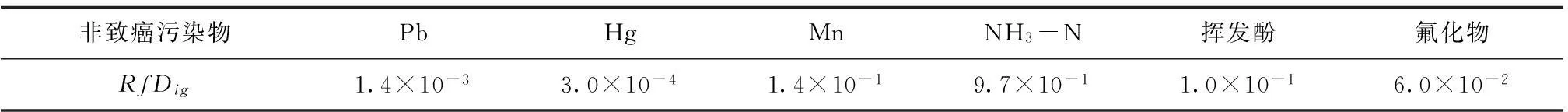
表2 非致癌污染物的参考剂量(饮水途径)
非致癌污染物PbHgMnNp-N挥发酚氟化物RfDig1.4×10-33.0×10-41.4×10-19.7×10-11.0×10-16.0×10-2
2.3 数据来源
地下水监测数据来源于2013—2014年该生活垃圾填埋场地下水现状调查项目,采样时间为2013年10月,2014年4月和7月,采样点位置见图2。
2.4 模型参数的三角随机模拟化处理
2.4.1 模型参数的三角模糊化处理
根据1.2.1节中三角模糊数的数据处理方法,分别对各监测井的监测数据进行处理,结果见表3。由表3可知,各井的监测数据经三角模糊化处理后,污染物浓度的最大值和最小值波动范围较大,表明其健康风险评价确实存在很大的不确定性。
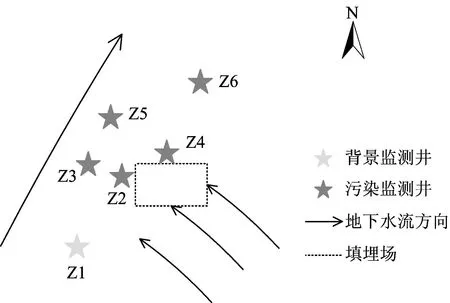
图2 采样点位置Fig.2 Study area and sampling sites
2.4.2 三角模糊数模型参数的随机模拟
根据1.2.2节中三角随机模拟的数据处理方法,利用Crystal ball®软件分别对表3数据所导致的成人及儿童的个人健康风险进行随机模拟,得到一系列符合正态分布的数值序列。由于模拟具有较高的随机性,为使模拟结果达到收敛,分别对各采样点数据进行10 000、20 000、30 000、40 000、50 000、60 000和80 000次的随机模拟。当模拟次数达到80 000次时,各监测井的有毒污染物所致健康风险值模拟结果均达到收敛,在各区间内的分布趋于稳定,模拟结果见表4。
表3 各监测井中污染物浓度监测数据三角模糊化处理结果
Table 3 The concentrations of pollutants in well treated by the triangular fuzzy numbers mgL
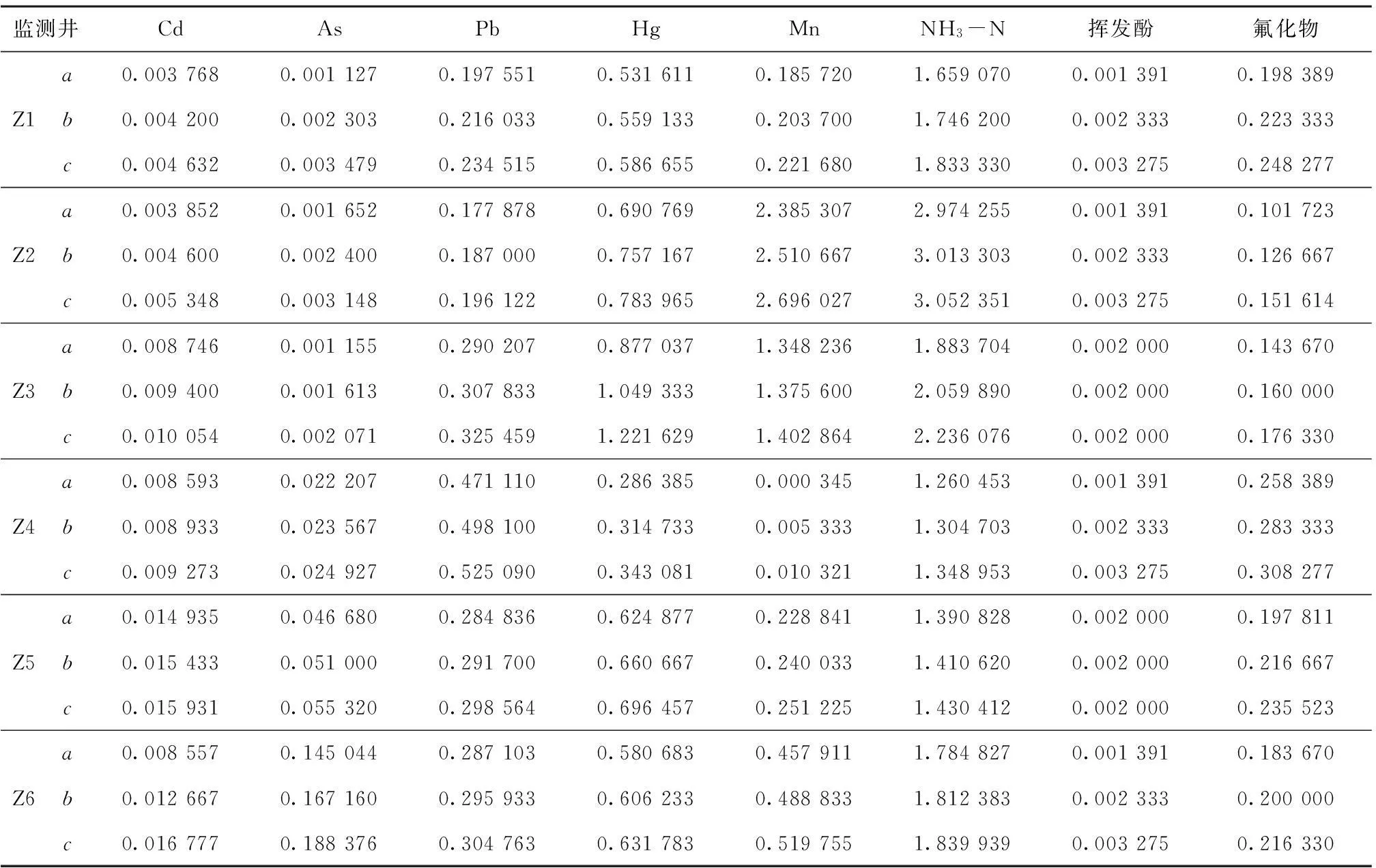
表3 各监测井中污染物浓度监测数据三角模糊化处理结果
监测井CdAsPbHgMnNp-N挥发酚氟化物Z1a0.0037680.0011270.1975510.5316110.1857201.6590700.0013910.198389b0.0042000.0023030.2160330.5591330.2037001.7462000.0023330.223333c0.0046320.0034790.2345150.5866550.2216801.8333300.0032750.248277Z2a0.0038520.0016520.1778780.6907692.3853072.9742550.0013910.101723b0.0046000.0024000.1870000.7571672.5106673.0133030.0023330.126667c0.0053480.0031480.1961220.7839652.6960273.0523510.0032750.151614Z3a0.0087460.0011550.2902070.8770371.3482361.8837040.0020000.143670b0.0094000.0016130.3078331.0493331.3756002.0598900.0020000.160000c0.0100540.0020710.3254591.2216291.4028642.2360760.0020000.176330Z4a0.0085930.0222070.4711100.2863850.0003451.2604530.0013910.258389b0.0089330.0235670.4981000.3147330.0053331.3047030.0023330.283333c0.0092730.0249270.5250900.3430810.0103211.3489530.0032750.308277Z5a0.0149350.0466800.2848360.6248770.2288411.3908280.0020000.197811b0.0154330.0510000.2917000.6606670.2400331.4106200.0020000.216667c0.0159310.0553200.2985640.6964570.2512251.4304120.0020000.235523Z6a0.0085570.1450440.2871030.5806830.4579111.7848270.0013910.183670b0.0126670.1671600.2959330.6062330.4888331.8123830.0023330.200000c0.0167770.1883760.3047630.6317830.5197551.8399390.0032750.216330
注:a,b,c分别为某一污染物浓度的最小可能值、最可能值和最大可能值。
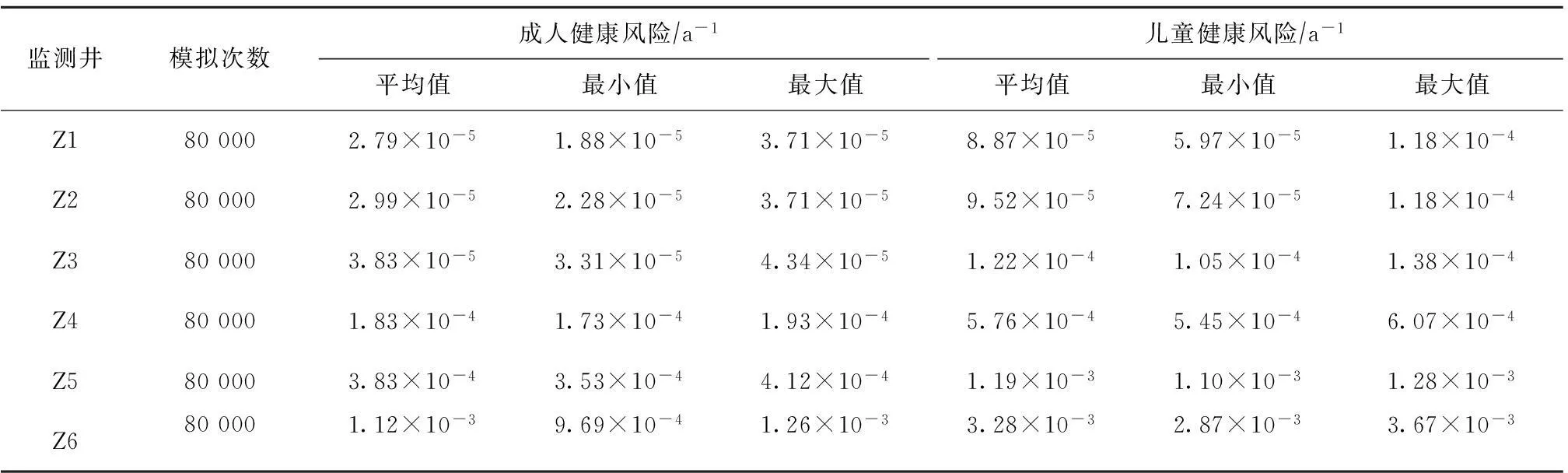
表4 各监测井有毒污染物所致健康风险随机模拟结果
2.5 结果与分析
2.5.1 评价结果
根据表1的健康风险评价标准,得出的各监测井隶属于健康风险等级的可能值区间、相应概率水平及其所处的风险等级,见表5。以Z2井的儿童健康风险为例的累积概率分布,见图3。
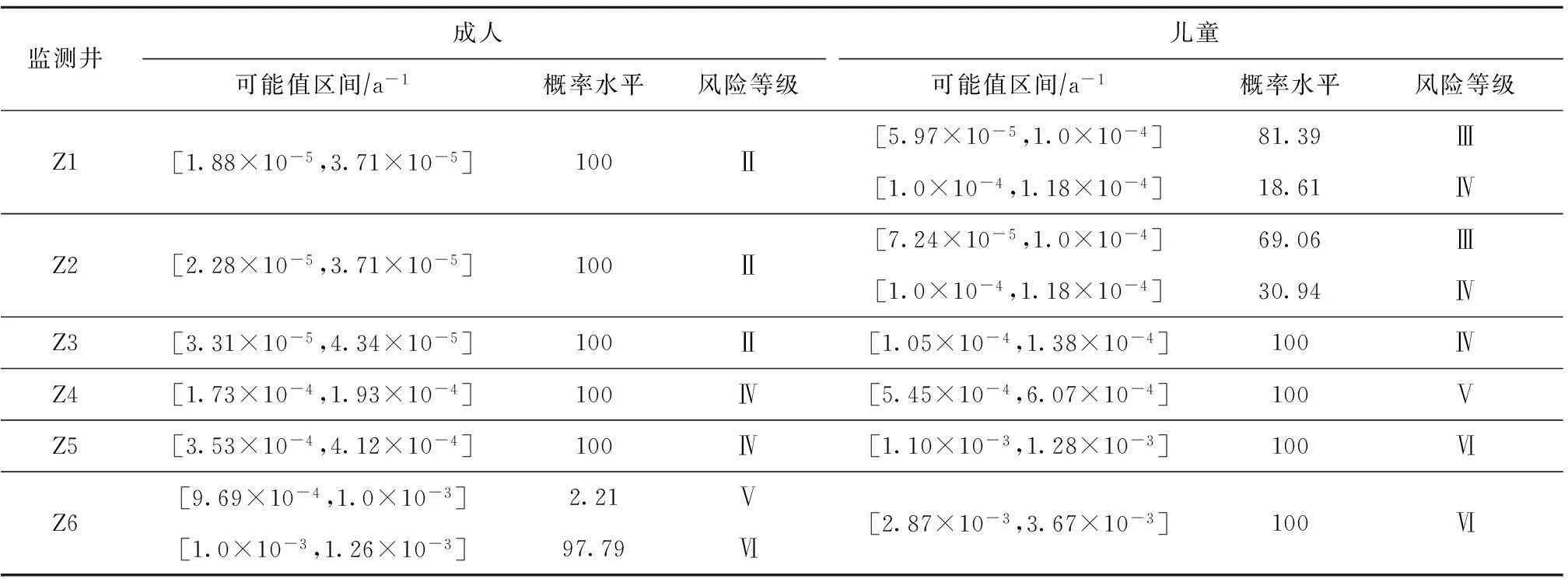
表5 各监测井健康风险的可能值区间及其相应概率水平
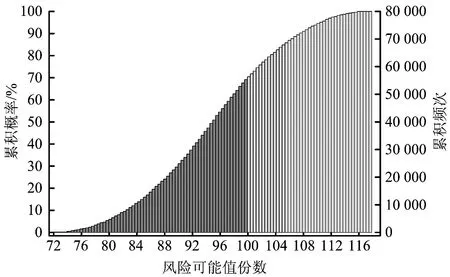
注:深色部分表示Z2井儿童健康风险处于Ⅲ级的累积概率为69.06%、累积频次为55 248次;浅色部分代表处于Ⅳ级的累积概率为30.94%、累积频次为24 752次。图3 Z2井的儿童健康风险累积概率分布Fig.3 The cumulative probability of Z2 well
结合表1和表5可知,该垃圾填埋场所布设的6个监测井的污染物所产生的个人健康风险值波动范围较大,成人的风险可能值区间有1口监测井处于2个风险等级之间,儿童的风险可能值区间有2口监测井处于2个风险等级之间,其余处于一个等级,最大值和最小值差距在0.1~1倍,由于地下水具有流动缓慢的特性,该数值表明研究区域内地下水污染物浓度随时间变化的波动性相对较大,健康风险值有较强的不确定性。采用本研究的三角随机模拟模型进行风险评价,在很大程度上降低因个别值过高或过低影响评价结果的情况发生,降低了预测结果的不确定性。从表5可以看出:只有Z1、Z2、Z3监测井成人健康风险值小于最大风险可接受水平(5.0×10-5a-1),处于可接受范围内;其余3口监测井成人健康风险值均超过最大风险可接受水平,处于不可接受范围;6口监测井儿童健康风险均超过最大风险可接受水平,全部不可接受。
Z1背景监测井儿童健康风险超过最大风险可接受水平,说明该生活垃圾填埋场地下水背景值风险等级已经处于不可接受范围;其余监测井风险值均不同程度大于Z1背景监测井,说明该垃圾填埋场造成附近地下水风险等级升高,该填埋场对地下水有污染现象;该处地下水对成人和儿童造成的健康风险已处于不可接受范围,应积极采取措施进行治理。
根据表5数据,结合表1及式(13),通过各等级概率水平进行赋值加权识别出其综合风险值,结果如表6所示。
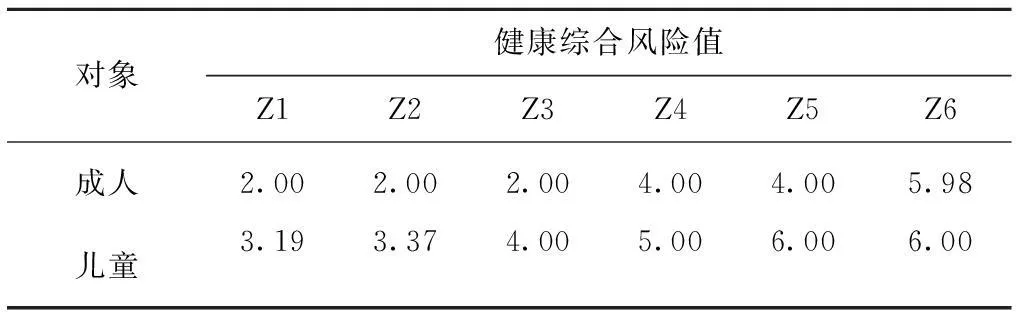
表6 各监测井健康综合风险值
由表6可知,Z6监测井的健康综合风险值最大,Z1背景监测井的健康综合风险值最小,其他几个监测井的健康综合风险值位于二者之间。
2.5.2 对比分析与讨论
为更加清楚地体现本研究模型在降低地下水健康风险不确定性方面的优势,将实例中的数据采用式(1)~(6)确定性评价方法进行各监测井的风险计算,结果如表7所示。
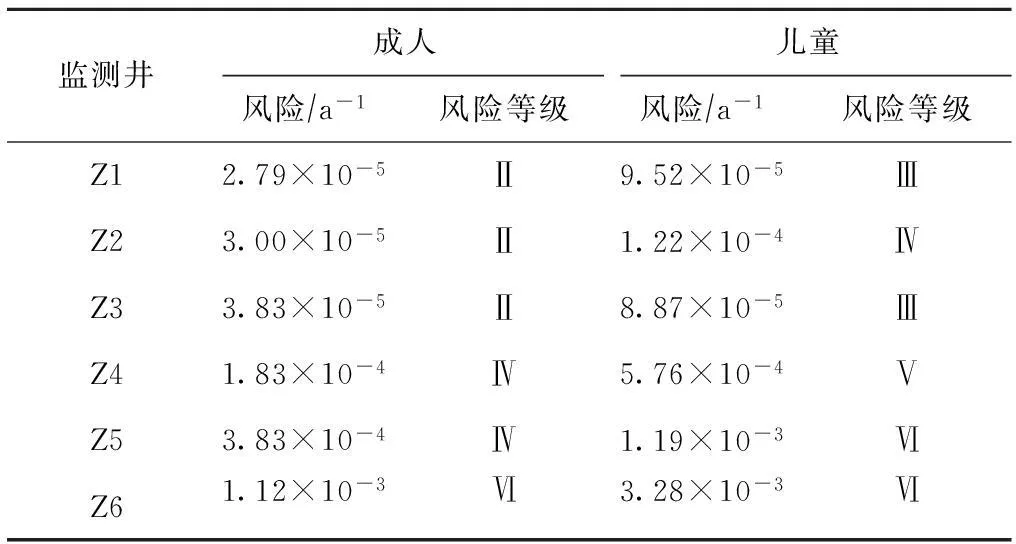
表7 确定性评价方法的各监测井的风险
对比表5与表7可知,各监测井风险值变化趋势基本一致。表7直接采用污染物的平均浓度进行评价,忽略了水环境中污染物浓度不断变化的特性,评价结果具有一定的不确定性。表5计算结果在原有蒙特卡罗方法和三角模糊数结合的方法基础上,建立了三角随机模拟模型,通过对监测井污染物浓度分布情况的随机模拟,不仅可以判定评价对象可能隶属的风险等级,而且可以定量得出其相应的概率水平,在一定程度上解决了评价过程中存在的不确定性问题,与传统的确定性评价模型相比,风险评价的结果能够更全面、合理地反映水环境健康风险水平的真实情况,具有较好的实用性和可操作性,能够为决策者提供更加科学客观的依据。
2.6 不确定性分析
2.6.1 参数选择的不确定性
在确定健康风险评价模型参数时,人均寿命取70 a;人均体质量,成人为70 kg,儿童为10 kg;日均饮水量,成人为2.2 L,儿童为1.0 L,这5个参数的选择具有不确定性,即该垃圾填埋场附近居民人均寿命、人均体质量、日均饮水量参数的选取并不具有唯一的确定值,因而参数的选择都会对风险评价结果产生或多或少的影响,即造成评价结果的不确定性。
2.6.2 模型本身的不确定性
选择的三角随机模拟模型,亦是对真实的情况进行简化后得到的,与实际发生的情况存在差异。
2.6.3 受体的不确定性分析
不同人群可以承受的风险水平各不相同,或者可以说受体(人)自身的特点对水中污染物的敏感程度也不尽相同,因此,评价所得的风险对个体健康的危害不确定。
3 结论
(1)将三角模糊数与Crystal ball®软件中的三角分布类型进行结合随机模拟,应用于生活垃圾填埋场地下水环境健康风险评价中,降低了传统确定性方法可能产生的误差,弥补了该填埋场可以获取的地下水水质数据资料较少和精确度不高的不足,在一定程度上解决了传统确定性评价过程中存在的不确定性问题。
(2)三角随机模拟模型在地下水环境健康风险评价领域的应用,与传统评价方法相比,具有计算简单快速、精度高的优点,并且不仅可以判定地下水污染可能隶属的风险等级,而且可以定量得出其相应的概率水平,为决策者提供更加综合的信息,为地下水污染管理工作提供依据。
(3)实例研究结果表明,各监测井的儿童健康风险均超过了可接受水平,Z4、Z5、Z6监测井的成人健康风险也超过了可接受水平,相关部门应开展有针对性的预防治理工作。对于造成危害的主要污染物的确定,还需进行深入的研究。
[1] 王淑扬.垃圾填埋场地下水污染健康风险评估方法研究[D].阜新:辽宁工程技术大学,2012:24.
[2] 张澄博.垃圾卫生填埋结构对地质环境效应的控制研究[J].地质灾害与环境保护,1999,10(增刊):68-128.
[3] 张英民,尚晓博,李开明,等.城市生活垃圾处理技术现状与管理对策[J].生态环境学报,2011,20(2):389-396.
ZHANG Y M,SHANG X B,LI K M,et al.Technologies status and management strategies of municipal solid waste disposal in China[J].Ecology and Environmental Sciences,2011,20(2):389-396.
[4] 洪梅,张博,李卉,等.生活垃圾填埋场对地下水污染的风险评价:以北京北天堂垃圾填埋场为例[J].环境污染与防治,2011,33(3):101-104.
[5] 刘蕊,张辉,勾昕,等.健康风险评估方法在中国重金属污染中的应用及暴露评估模型的研究进展[J].生态环境学报,2014,23(7):1239-1244.
LIU R,ZHANG H,GOU X,et al.Approaches of health risk assessment for heavy metals applied in China and advance in exposure assessment models: a review[J].Ecology and Environmental Sciences,2014,23(7):1239-1244.
[6] 李鸣晓,安达,杨昱,等.白洋淀淀中村非规范垃圾堆放地下水污染健康风险评价[J].环境工程技术学报,2012,2(5):449-455.
LI M X,AN D,YANG Y, et al.Groundwater pollution health risk assessment at non-formal solid waste dumping sites of a village in Baiyangdian Lake[J].Journal of Environmental Engineering Technology,2012,2(5):449-455.
[7] 金菊良,吴开亚,李如忠.水环境风险评价的随机模拟与三角模糊数耦合模型[J].水利学报,2008,39(11):1257-1261.
JIN J L,WU K Y,LI R Z.Coupling method of stochastic simulation with triangular fuzzy numbers for water environment risk assessment[J].Journal of Hydraulic Engineering,2008,39(11):1257-1261.
[8] 李如忠,洪天求,金菊良.河流水质模糊风险评价模型研究[J].武汉理工大学学报,2007,29(2):43-46.
LI R Z, HONG T Q,JIN J L.Research on fuzzy risk assessment model for river water quality[J]. Journal of Wuhan University of Technology,2007,29(2):43-46.
[9] 陈光怡,丁莉,张寅,等.地下水开采可靠性的随机模拟与三角模糊数耦合模型[J].安徽建筑工业学院学报,2009,17(6):84-87.
CHEN G Y,DING L,ZHANG Y,et al.The reliability of groundwater exploitation and the stochastic simulation model of triangular fuzzy numbers coupled[J].Journal of Anhui Institute of Architecture & Industry,2009,17(6):84-87.
[10] GIACHETTI R E,YOUNG R E.A parametric representation of fuzzy numbers and their arithmetic operators[J].Fuzzy Sets and Systems,1997,91(2):185-202.
[11] 曾光明,卓利,钟政林,等.水环境健康风险评价模型及其应用[J].水电能源科学,1997,15(4):29-34.
ZENG G M, ZHUO L,ZHONG Z L,et al.Assessment models for water environmental health risk analysis[J].Water Resources and Power,1997,15(4):29-34.
[12] AGUSA T,KUNITO T,FUJIHARA J,et al.Contamination by arsenic and other trace elements in tube-well water and its risk assessment to humans in Hanoi,Vietnam[J].Environmental Pollution,2006,139(1):95-106.
[13] TCHOUNWOU P B,CENTENO J A,PATLOLLA A K.Arsenic toxicity, mutagenesis, and carcinogenesis:a health risk assessment and management approach[J].Molecular and Cellular Biochemistry,2004,255(12):47-55.
[14] 张建龙,解建仓,汪妮,等.再生水回用的改进健康风险评价及土壤承载能力研究[J].水土保持学报,2010,24(2):192-196.
ZHANG J L,XIE J C,WANG N,et al.Study on reclaimed water reuse of improve health risk assessment and soil carrying capacity[J].Journal of Soil and Water Conservation,2010,24(2):192-196.
[15] ZADEH L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[16] 盛骤,谢式千,潘承毅.概率论与数理统计[M].杭州:浙江大学出版社,2001:150-198.
[17] 高继军,张力平,黄圣彪,等.北京市饮用水源水重金属污染物健康风险的初步评价[J].环境科学,2004,25(2):47-50.
GAO J J,ZHANG L P,HUANG S B,et al.Preliminary health risk assessment of heavy metals in drinking waters in Beijing[J].Environmental Science,2004,25(2):47-50.
[18] GIACHETTI R E,YOUNG R E.Analysis of the error in the standard approximation used for multiplication of triangular and trapezoidal fuzzy numbers and the development of a new approximation[J].Fuzzy Sets and Systems,1997,91(1):1-13.
[19] 李宝山,张义平.蒙特卡洛法在软岩巷道支护中的应用[J].煤炭工程,2009(11):71-72.
[20] 祝慧娜.基于区间数的水环境健康风险模糊综合评价[D].长沙:湖南大学,2009:31-32 ▷
Assessment Model of Landfill Sites Groundwater Environmental Health Risk Based on Stochastic Simulation-triangular Fuzzy Numbers
WANG Yue1, AN Da1, XI Beidou1, TANG Jun1, LIANG Huanhuan1,2, ZHANG Boqiang1,3
1.State Environmental Protection Key Laboratory of Simulation and Control of Groundwater Pollution,Chinese Research Academy of Environmental Sciences, Beijing 100012, China 2.College of Environmental and Chemical Engineering, Shanghai University, Shanghai 200444, China 3.College of Water Resources and Environment Engineering, Donghua Polytechnic University, Nanchang 330013, China
On the basis of US EPA health risk assessment method, and coupling the methods of triangular fuzzy number and stochastic simulation, the Stochastic Simulation-triangular Fuzzy Numbers Model was built up and applied in groundwater environmental health risk assessment for a domestic waste landfill site in northern China as a case study. The results showed that the children′s health risks of six monitoring wells all exceed the acceptable level, and the values of wells Z1 and Z2 distributed in Level Ⅲ and Level Ⅳ interval. The adults′ health risks of three monitoring wells also exceed the acceptable level, and the values of well Z6 distributed in Level Ⅴ and Level Ⅵ interval. Compared with that by the deterministic method, this model in a certain extent solved the uncertainty problem existing in the traditional deterministic evaluation process. It could not only calculate the risk level of groundwater pollution, but also quantitatively obtain the corresponding probability level, providing more accurate assessment information of the health risks for the decision makers and more basis for the groundwater pollution management.
stochastic simulation-triangular fuzzy number; landfill site; groundwater; health risk assessment
GAO Z G,ZHU J,WENG Y B.Comprehensive assessment of ecosystem health on multiple scales:a case study for metropolitan area of Ningbo[J].Acta Ecologica Sinica,2010(7):1706-1717. ○王月,安达,席北斗,等.基于三角随机模拟的生活垃圾填埋场地下水环境健康风险评价模型[J].环境工程技术学报,2016,6(1):49-56.
WANG Y, AN D, XI B D, et al.Assessment model of landfill sites groundwater environmental health risk based on stochastic simulation-triangular fuzzy numbers[J].Journal of Environmental Engineering Technology,2016,6(1):49-56.
2015-08-20
环境保护部全国地下水基础环境状况调查评估项目(144130012110302)
王月(1982—),女,工程师,硕士,主要从事地下水污染健康风险评价,yuewangg@163.com
*责任作者:安达(1979—),女,副研究员,博士,主要从事地下水污染风险评估,anda7977@163.com
X523
1674-991X(2016)01-0049-08
10.3969j.issn.1674-991X.2016.01.008

