城市轨道交通同步协调的优化模型

曹志超　袁振洲　李得伟

(1北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京　100044)(2北京交通大学轨道交通控制与安全国家重点实验室，北京　100044)



城市轨道交通同步协调的优化模型

曹志超1，2袁振洲1李得伟2

(1北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044)
(2北京交通大学轨道交通控制与安全国家重点实验室，北京100044)

摘要:为实现换乘客流的无缝衔接和列车到发的同步协调，以总换乘等车时间最少为目标，将列车行车间隔、客流划分结果和等车时间作为主要输入条件，构建了带有0-1决策变量的城市轨道交通同步协调优化模型．运用改进的遗传算法与计算机模拟相结合的方法有效解决了模型的求解问题．最后，以北京市城市轨道交通为例进行仿真，输出整点发车和非整点发车条件下的2种优化方案．结果表明，整点发车方案和非整点发车方案的总换乘等车时间较基础方案分别缩短2．26%和2．48%，单个车站的最大换乘等车时间分别节省了7．90%和12．87%．该优化模型能够有效缩短乘客的换乘等车时间，提高城市轨道交通的服务水平．

关键词:城市轨道交通;同步协调;列车时刻表;无缝衔接;换乘等车时间

引用本文:曹志超，袁振洲，李得伟．城市轨道交通同步协调的优化模型［J］．东南大学学报(自然科学版)，2016，46(1) : 221－225．DOI: 10．3969/j．issn．1001－0505．2016．01．036．

列车时刻表编制是城市轨道交通运输计划的重要内容．在网络条件下，尤其是客流高峰期高密度行车环境下，实现列车到发的同步协调，减少乘客因换乘而导致的等车时间是列车时刻表优化的重要目标．鉴于网络条件下不同线路间换乘设施走行时间的动态性以及列车到发同步调整的复杂性，如何科学合理地优化列车时刻表一直是学术界和轨道运营管理者们研究的热点问题．

国外学者研究列车时刻表同步协调问题时主要采用以下2种方法:①基于客流分配的方法，其目标函数为最小化乘客总换乘等车时间．例如，Wong等［1］通过调整列车的在途时间、停站时间和发车间隔来实现目标优化，基于0-1变量定义接驳成功的列车; Shafahi等［2］采用最小公约数的方法得到了多条换乘线路平均换乘等车时间，并通过引入额外等车时间以进一步优化列车时刻表．②基于列车到发衔接的方法，其目标函数为最大化列车衔接的换乘同步成功的次数．此处，学者们对换乘同步成功的定义各不相同，Ceder等［3］提出的模型仅适用于简单网络，且求解为试算法，精确性较差; Ibarra-Rojas等［4］通过优化提出了准确算法．

国内关于同步协调优化问题的相关研究较少，模型主要以换乘等车时间最小化为目标．周艳芳等［5］增加了换乘不满意度最低的模型目标;曹志超等［6］增加了列车承载能力的约束．现阶段研究尚无法实现全网络交通的同步协调优化．

本文基于正态分布的换乘客流到达规律，结合基本行车约束和准确划分换乘客流的计算方法，构建了带有0-1决策变量的同步协调的优化模型，并提出了求解算法．

1　模型构建

1．1问题描述

令城市轨道交通列车运行网络拓扑G = (L，S，Q)，其中，L = { 1，2，…，M}为线路集，S = { 1，2，…，N}为车站集，Q = { 1，2，…，B}为列车集．令研究时段为T．

换乘等车时间是指乘客因换乘的需要，从列车下车通过换乘设施到达接驳列车的站台开始，等待最近一班接驳列车所花费的时间．

2)当线路i上列车p到达车站n时，接驳列车2尚未发车，但乘客通过换乘设施后接驳列车2已发车，即，则换乘乘客不能上车．

3)乘客从线路i上列车p下车，通过换乘设施后，接驳列车4未发车，但之前已有列车3进行接驳，即为线路j上列车在车站n的停站时间，则列车p的换乘乘客不能被列车4接驳．

图1　城市轨道交通2条线路同步协调换乘示意图

列车接驳成功是指乘客到达接驳列车所在站台后发现列车恰好在停车等待．基于上述分析，列车接驳成功的条件须严格满足

1．2目标函数

基于给定的换乘客流量，模型以最小化乘客的总换乘等车时间为目标，即

1．3约束条件

1．3．1行车约束

列车时刻表的编制应满足基本行车约束，如安全追踪间隔约束、首末班车出发时刻约束、列车到发时刻与发车间隔的运算关系约束等［7－9］．

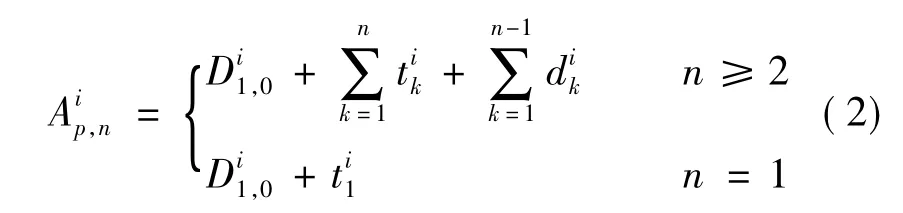
连续2班列车的出发时刻应满足列车安全追踪间隔时间约束，即

式中，H为列车安全追踪间隔时间．

首末班车的出发时刻须控制在研究时段的第1个和最后1个发车间隔区间内．假定研究时段T内，线路i上列车发车间隔hi固定不变，则

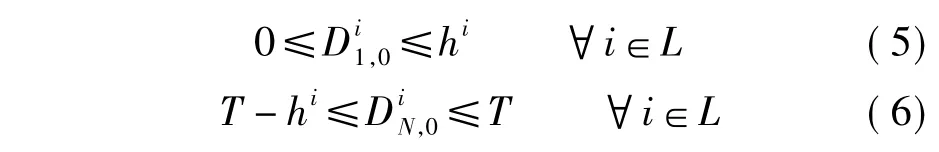
列车发车间隔的运算关系为

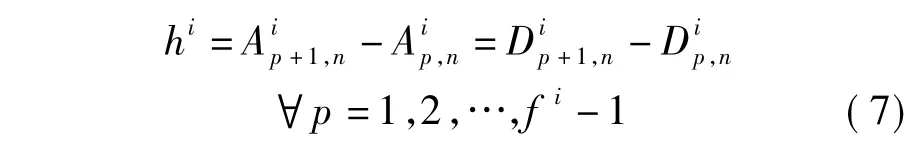
1．3．2客流划分

由于组成客流的乘客个体具有异质性，不同乘客具有不同的年龄、性别、结伴特征及携带行李特征，因此，即使同一班列车的客流通过换乘设施，不同乘客个体到达换乘站台的时间也存在一定差异．令客流在换乘设施的走行时间域为其中分别为车站n处乘客从线路i换乘到线路j走行时间的最小值和最大值，且

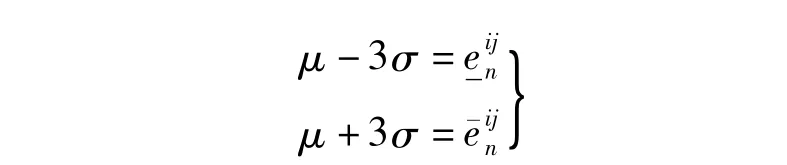
可得

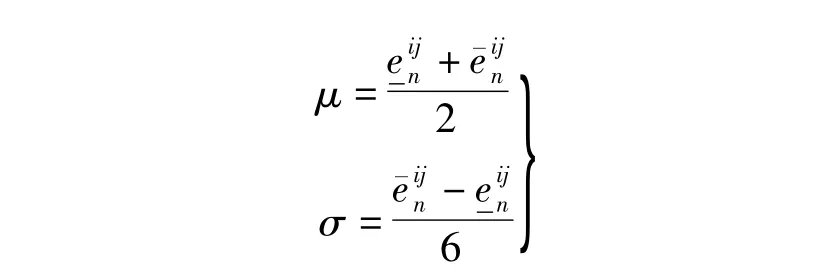
换乘走行时间将影响接驳列车的上车人数，具体可分为以下2种情况:

1)所有下车乘客均成功换乘到某一列车(见图2(a) )．从列车p下车的换乘乘客中，步行时间最长的乘客在接驳列车q发车之前到达，即满足

2)换乘乘客走行速度不一，速度较快的乘客换乘到某一列车，剩余乘客换乘到下一列车(见图2(b) )．换乘客流被划分为2个部分．速度较快的客流可以换乘到列车q，对应于图2(b)中左侧阴影部分，客流量表示为剩余客流需多等待一个发车间隔hi，客流量表示为即

换乘客流量计算公式为

式中，Φ为正态分布的概率．

图2　客流划分示意图

1．3．3等车时间

基于客流划分的结果，不同情况下客流换乘的列车不同，其等车时间计算方法也不同，具体如下:

情况1

情况2

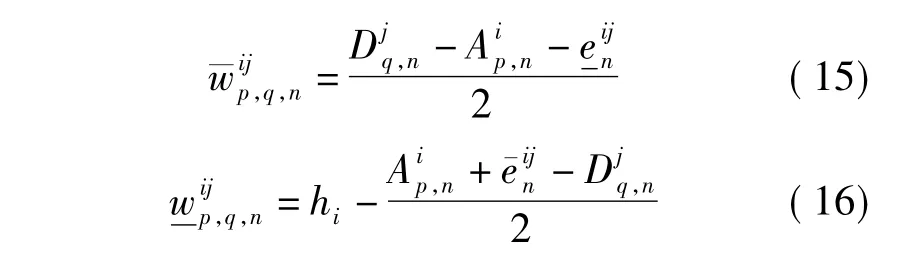
2　求解算法

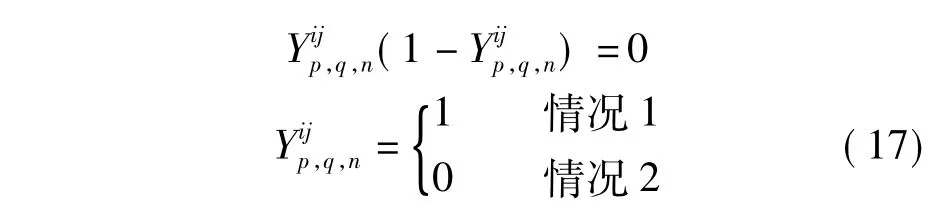
则目标函数可转化为

本文采用改进的遗传算法求解以上模型．其核心思想为:选取i∈L，j∈L时首班列车出发时刻为00: 00的方案作为基础方案，并将其作为初始解，迭代求较优解;令线路上的首班列车出发时刻为决策变量．具体求解步骤如下:

②基因设置．运营线分上行和下行，故染色体集合为2M．选择所有线路上的首班列车出发时刻组成的集合作为基因．根据约束(2)～(7)，求得城市轨道网络中所有列车在每个站的到发时刻．

③适应度函数．将模型目标函数作为适应度函数，即

④交叉与变异．在发车间隔［0，hi］内对

进行随机取值，分别进行客流划分计算和等车时间计算，求得适应度值Z．比较Z与Zt，如果Z值更优，则记录Zt= Z;否则，继续迭代寻找，且t = t +1．

⑤较优解．在限定的时间或迭代次数内，适应度值已收敛且不能更优，则停止迭代，认为为较优解．

3　算例

北京市城市轨道交通某运营期内开行16条双向线路，共设235个车站，其中38个为换乘站．假设各运营线的列车在途时间和停站时间均已知．选取的研究时段T为高峰时段中的1 h．根据本文所提模型，利用Matlab软件对问题进行求解．分别将整数决策变量和实数决策变量作为整点发车方案和非整点发车方案进行优化，其优化单位分别为60和1 s．通过对算法中迭代参数的不断试验和模拟，在个体数量为20、代沟为0．8、变异率为0．5的1 000次迭代中求得较优解．2种方案的优化结果与基础方案结果的对比见表1．基础方案、整点发车方案和非整点发车方案的总换乘等车时间分别为735 112，718 838，717 311 min．对比发现，在总换乘等车时间上，整点发车方案和非整点发车方案比基础方案分别节省了16 274和17 801 min，较基础方案分别优化了2．21%和2．42%．

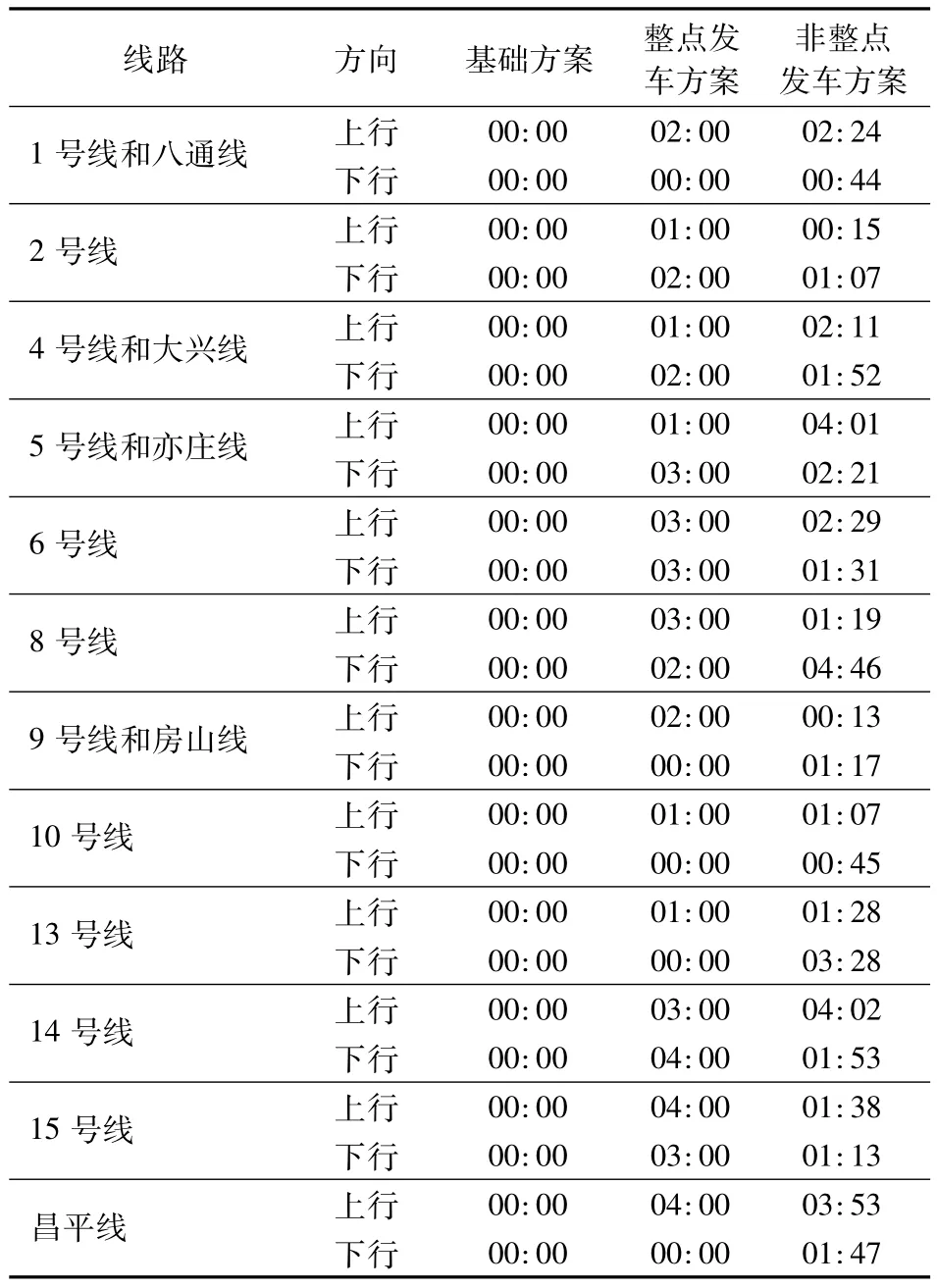
表1　北京市城市轨道交通列车时刻表优化结果

进一步对比全网5个换乘量最大的车站的总换乘等车时间，结果见图3．由图可知，各换乘站的总换乘等车时间均减少．以换乘客流量最大的车站西直门站为例，与基础方案相比，整点发车方案和非整点发车方案的最大换乘等车时间分别节省了7．90%和12．87%．

研究发现，通过优化城市轨道交通的列车时刻表，能够有效缩短乘客的换乘等车时间，增加换乘线路间列车的接驳成功次数，实现更多换乘乘客的无缝衔接，从而提高城市轨道交通的换乘效率和乘客服务水平．

图3　不同换乘站的换乘等车时间

4　结语

城市轨道交通的同步协调控制是列车时刻表编制的重要内容，是网络化运输组织协调性的具体体现．本文对城市轨道交通换乘站的换乘客流进行了准确划分，提出了针对性的换乘等车时间计算方法，构建了以乘客总换乘等车时间最少为目标的列车时刻表优化模型，解决了既有研究换乘走行时间计算误差大或换乘客流划分模糊的问题，从而使计算更加高效和准确．实例证明，利用所提模型可实现换乘站列车的同步到发和网络的协调控制，有效缩短了乘客的换乘等车时间，提高了城市轨道交通的服务水平．本文所研究的场景主要针对发车间隔不变的条件，对于动态发车间隔条件下的列车时刻同步问题将是下一步的研究内容．

参考文献(References)

［1］Wong R C W，Yuen T W Y，Fung K W，et al．Optimizing timetable synchronization for rail mass transit ［J］．Transportation Science，2008，42(1) : 57－69．DOI: 10．1287/trsc．1070．0200．

［2］Shafahi Y，Khani A．A practical model for transfer optimization in a transit network: Model formulations and solutions［J］．Transportation Research Part A: Policy and Practice，2010，44(6) : 377－389．DOI: 10．1016/ j．tra．2010．03．007．

［3］Ceder A，Golany B，Tal O．Creating bus timetables with maximal synchronization［J］．Transportation Research Part A: Policy and Practice，2001，35 (10) : 913－928．

［4］Ibarra-Rojas O J，Rios-Solis Y A．Synchronization of bus timetabling［J］．Transportation Research Part B: Methodological，2012，46 (5) : 599－614．DOI: 10．1016/j．trb．2012．01．006．

［5］周艳芳，周磊山，乐逸祥．城市轨道网络换乘站列车衔接同步协调优化研究［J］．铁道学报，2011，33 (3) : 9－16．DOI: 10．3969/j．issn．1001－8360．2011．03．002．Zhou Yanfang，Zhou Leishan，Yue Yixiang．Synchronized and coordinated train connecting optimization for transfer stations of urban rail networks［J］．Journal of the China Railway Society，2011，33(3) : 9－16．DOI: 10．3969/j．issn．1001－8360．2011．03．002．(in Chinese)

［6］曹志超，袁振洲，李得伟，等．结合列车时间表的地铁换乘同步性优化［J］．现代城市轨道交通，2014 (5) : 59－62，74．DOI: 10．3969/j．issn．1672－7533．2014．05．016．Cao Zhichao，Yuan Zhenzhou，Li Dewei，et al．Optimization for metro interchange synchronization with consideration of train timetable［J］．Modern Urban Transit，2014(5) : 59－62，74．DOI: 10．3969/j．issn．1672－7533．2014．05．016．(in Chinese)

［7］Ceder A，Marguier P H J．Passenger waiting time at transit stops［J］．Traffic Engineering and Control，1985，26(6) : 327－329．

［8］Niu H，Zhou X．Optimizing urban rail timetable under time-dependent demand and oversaturated conditions ［J］．Transportation Research Part C: Emerging Technologies，2013，36: 212－230．DOI: 10．1016/j．trc．2013．08．016．

［9］李得伟，韩宝明，李晓娟，等．基于节点服务的高速铁路列车停站方案优化模型［J］．铁道学报，2013，35 (6) : 1－5．DOI: 10．3969/j．issn．1001－8360．2013．06．001．Li Dewei，Han Baoming，Li Xiaojuan，et al．Highspeed railway stopping schedule optimization model based on node service［J］．Journal of the China Railway Society，2013，35 (6) : 1－5．DOI: 10．3969/j．issn．1001－8360．2013．06．001．(in Chinese)

［10］Liu Z，Shen J，Wang H，et al．Regional bus timetabling model with synchronization［J］，Journal of Transportation Systems Engineering＆Information Technology，2007，7(2) : 109－112．DOI: 10．1016/ S1570－6672(07) 60018-X．

Synchronization and coordination optimization model of urban rail transit

Cao Zhichao1，2Yuan Zhenzhou1Li Dewei2
(1MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology，Beijing 100044，China)
(2State Key Lab of Rail Traffic Control and Safety，Beijing Jiaotong University，Beijing 100044，China)

Abstract:In order to achieve the seamless connections of passengers and the synchronization and coordination of arrival and departure of trains，a synchronization and coordination optimization model of urban rail transit(URT) with 0-1 binary decision variables was proposed．The objective is the minimization of the total transfer waiting time and the inputs are the running interval，the results of passenger division and the waiting time．The model was solved by combining the improved genetic algorithm with computer simulation．Finally，Beijing URT was simulated for case study．Two optimization strategies，the minute-departure scheme and the second-departure scheme，were described．The results show that compared with the traditional scheme，the total waiting time of the transfer passengers of the minute-departure scheme and the second-departure scheme is decreased by 2．26% and 2．48%．The maximum transfer waiting time at one station is reduced by 7．90% and 12．87%．The proposed model is effective to decrease the transfer waiting time and to improve the service level．

Key words:urban rail transit; synchronization and coordination; timetable; seamless connection; transfer waiting time

基金项目:国家重点基础研究发展计划(973计划)资助项目(2012CB725403)、北京市自然科学基金资助项目(9132015)、教育部高等学校基本科研业务费资助项目(2014JBZ008)、北京高等学校青年英才计划资助项目(YETP0555)、北京交通大学轨道交通控制与安全国家重点实验室自主课题资助项目(RCS2014ZTY1)．

收稿日期:2015-06-23．

作者简介:曹志超(1988—)，男，博士生;袁振洲(联系人)，男，博士，教授，博士生导师，zzyuan@ bjtu．edu．cn．

DOI:10．3969/j．issn．1001－0505．2016．01．036

中图分类号:U121

文献标志码:A

文章编号:1001－0505(2016) 01-0221-05