尖轨降低值超限对转辙器动力特性的影响研究

马晓川， 王 平， 王 健， 徐井芒

(西南交通大学 高速铁路线路工程教育部重点实验室， 四川 成都 610031)

高速道岔转辙器处，由于尖轨顶面降低，开始阶段的轮轨接触点位于基本轨上，并随尖轨顶宽的增大逐渐外移，直到轮轨接触点由基本轨过渡到尖轨上。这个过程中，轮对在横向蠕滑力的作用下会向尖轨方向偏离。当轮对中心偏离轨道中心线时，左右车轮将以不同的滚动圆半径向前运行，轮对中心的运动轨迹呈波形曲线，称为轮对的蛇行运动[1-2〗。道岔转辙器处的动力性能是道岔研究内容的重点，当轮对发生摆动时会恶化轮轨动力作用。

尖轨降低的位置和大小是影响道岔转辙器动力特性的重要因素，许多学者针对转辙器的动力特性进行了研究。文献[3〗提出了求解道岔转辙器轮载分布规律的计算模型和方法。文献[4〗提出了车辆道岔系统动力学理论。文献[5〗运用车辆道岔系统动力学的方法，研究了转辙器轨距优化技术对高速道岔动力性能的影响。文献[6〗建立了道岔动力参数设计法，并对道岔转辙器部分的轨距加宽进行了优化设计。

本文针对42号高速道岔存在尖轨降低值超限的问题，运用车辆-道岔系统动力学理论，通过仿真计算研究尖轨降低值超限对道岔转辙器处轮载过渡、车辆稳定、轮轨动力附加力、行车安全指标等的影响。

1 尖轨降低值及轮廓变化

1.1 尖轨降低值测量结果

使用深度尺对42号高速道岔直尖轨相对于曲基本轨的顶面降低值逐枕进行了测量，测量降低值与设计降低值的对比见图1。可见，该道岔直尖轨实际降低值普遍大于设计值，特别是在轮载从基本轨向尖轨过渡的范围内降低值偏差较大，最大值约2.3 mm，已超过TB/T3302—2013《高速铁路无砟轨道道岔铺设技术条件》[1〗中“尖轨与基本轨顶面高度偏差不大于1 mm”的规定。

动车组以295 km/h的速度直向通过该道岔时，在转辙器处会出现较为严重的晃车现象。根据尖轨降低值的偏差，在尖轨轨底和滑床台板之间设置不同厚度的铁垫片使尖轨抬高。由于现场条件及道岔本身结构的限制，调整后的尖轨降低值与设计降低值存在一定的偏差，但偏差被控制在1 mm之内。

1.2 尖轨轮廓变化

当实测尖轨降低值与设计降低值不符时，尖轨和基本轨的“组合轮廓”会随之发生变化。根据测得的尖轨降低值的偏差，分别得到尖轨顶宽20、35、50 mm三个关键断面处的轮廓变化，见图2。

2 计算理论

参考文献[4〗和文献[8〗，建立车辆-道岔系统耦合振动模型。该模型包含3个部分，分别是车辆模型、道岔模型和轮轨接触模型。

2.1 车辆模型

道岔区的车辆模型与区间线路的车辆模型相同。本文为了更好地模拟车辆经过道岔时的动力特性，采用整车模型。车辆模型见图3。

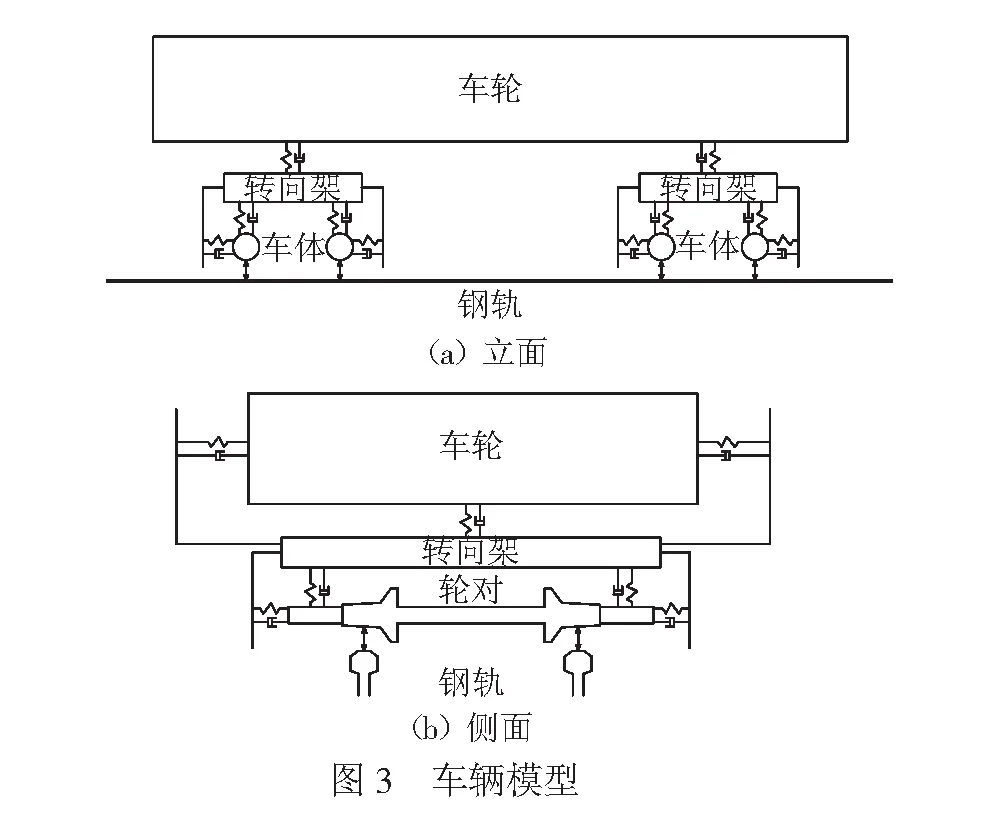
在车辆模型中，考虑31个运动自由度：车体有横移、沉浮、侧滚、点头和摇头5个自由度；2个转向架分别有横移、沉浮、侧滚、点头和摇头5个自由度;4个车轮分别有横移、沉浮、侧滚和摇头4个自由度。

计算模型坐标系的选取为：以车辆前进方向为x轴正方向，以车辆前进方向的右侧为y轴正方向，z轴正方向根据右手法则确定。

车辆的基本计算参数包括车体、转向架和轮对的质量，绕各轴的惯性矩，一、二系悬挂的刚度和阻尼。本文的车辆基本计算参数取自文献[8〗，见表1。

表1 车辆基本计算参数

2.2 道岔模型

根据42号高速道岔的设计图建立42号可动心轨高速道岔整体模型，见图4。

在道岔模型中，将道岔中的每根钢轨按轨枕支承点划分为有限个梁单元，每个单元节点有垂向位移、垂向转角、横向位移及横向转角4个自由度。轨枕在横向上被视为一个刚体质量块，具有横向位移1个自由度。在垂向上将轨枕按钢轨支承点划分为有限个梁单元，每个单元具有垂向位移和垂向转角2个自由度。

42号高速道岔的基本计算参数见表2。

表2 道岔基本计算参数

2.3 轮轨接触模型

车辆模型和道岔模型之间由轮轨接触模型建立关联。在轮轨接触模型中，考虑车轮与钢轨踏面的接触关系、车轮轮缘与钢轨的接触关系和车轮轮背与翼轨的接触关系。同时，考虑车辆运行至道岔不同部位时接触轨迹的变化。

轮轨垂向作用由非线性的赫兹接触弹簧力反映，轮轨横向作用由轮轨蠕滑力和轮缘力等反映，考虑车轮与基本轨、尖轨以及车轮与翼轨、心轨可能发生的多点接触情况。

2.4 振动方程

采用变分形式的最小势能原理方法，建立道岔轮轨振动系统的微分方程。由最小势能原理可知，在所有满足边界条件的协调位移中，满足平衡条件的位移可以使系统的总势能π达到极值，即

δπ=δ(U+V)=0

( 1 )

式中:U、V分别为系统的总应变能和总外力势能。

以大地为参考坐标系，以轨道及车辆均不受外力状态为初始状态，推导系统中各个能量的变分表达式及变分形式的位移协调条件，经计算机对号入座形成系统的质量矩阵M、刚度矩阵K及阻尼矩阵C，并组成系统的振动微分方程如式( 2 )所示

( 2 )

利用系统的振动微分方程，在某一时间步长下，迭代判断协调位移能否满足系统平衡条件。若不满足则重新组建新的振动微分方程，直到满足要求为止。如此可得到该时刻的系统振动响应。

2.5 计算模型验证

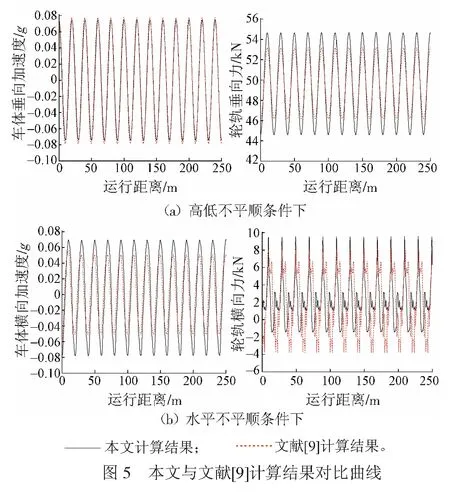
文献[10〗中建立了车辆-轨道空间模型，并通过与NUCARS和SIMPACK商业软件数值仿真结果的对比验证了其计算结果的可靠性。车辆进入道岔前，本文的计算结果与文献[9〗计算结果的对比见图5。计算时车速取为160 km/h，轨道不平顺采用的是单一的谐波型高低和方向不平顺，该不平顺可按式( 3 )进行描述

Y=0.5Asin(2πx/λ)

( 3 )

式中：A为不平顺的全峰值，取为10 mm；λ为不平顺波长，取为20 m；x为线路的纵向距离。

由图5可见:当轨道只存在高低不平顺时，与文献[10〗计算结果相比，本文计算结果中车体的垂向加速度基本吻合，轮轨垂向力的波动范围略大，两者的变化规律大致相同；当轨道只存在水平不平顺时，与文献[9〗计算结果相比，本文计算结果中车体横向加速度的波动范围略大，轮轨横向力的最大值略大，两者的变化规律大致相同。这说明本文所使用的计算模型可以较为真实可靠地反映车辆-轨道系统的振动特性。

3 计算结果分析

本文的计算是基于车辆-道岔系统动力学理论，应用SIMPACK动力学软件，通过仿真计算可分别得到动车组车辆以295 km/h的速度直向通过道岔和以120 km/h的速度侧向通过道岔时，道岔钢轨接触点的位移、轮对横向位移、车体横向加速度、轮轨横向及垂向动力附加力、脱轨系数、减载率等道岔动力性能参数。

3.1 转辙器轮载过渡

基于轮轨接触迹线法[11-12〗的基本原理，计算得到设计尖轨降低值条件下与尖轨降低值超限条件下尖轨关键断面处轮轨接触点对分布的对比，设计尖轨降低值条件下轮轨接触点对的分布见图6，尖轨降低值超限条件下轮轨接触点对的分布见图7。

车辆经过道岔转辙器时，开始阶段轮轨接触点主要分布在基本轨上，当车轮位于转辙器轮载过渡段时，轮轨接触点逐渐由基本轨过渡到尖轨上，最后轮轨接触点全部过渡到尖轨上。

图8所示为车轮从尖轨尖端运行到到尖轨跟端过程中，车轮荷载在基本轨上的比例系数变化规律。可见车轮荷载完全作用在基本轨上时，比例系数为1；反之，车轮荷载完全作用在尖轨上时，比例系数为0。

由图8可知：设计尖轨降低值条件下，轮载过渡段在距尖轨14.236～14.822 m，过渡段长度约586 mm；尖轨降低值超限条件下，轮载过渡段在距尖轨18.393～18.507 m，长度约为114 mm，与设计尖轨降低值条件相比明显后移和缩短。这说明尖轨降低值超限使得轮载过渡的起点后移且发生轮载过渡的时间明显减小。

由图6～图8可知，尖轨顶宽35 mm断面处，设计尖轨降低值条件下，轮轨接触点已由基本轨全部过渡到尖轨上，尖轨降低值超限条件下，轮轨接触点依然分布在基本轨上，说明尖轨降低值超限引起轮载过渡段的起点后移。

设计尖轨降低值条件、降低值超限调整前及调整后3种工况下计算的钢轨接触点位置的变化规律见图9。

由图9(a)可知：直股行车时，开始阶段钢轨接触点不断外移，设计尖轨降低值条件下，钢轨接触点的外移幅值为23.3 mm；尖轨降低值超限调整前，钢轨接触点的外移幅值达到38.7 mm，为设计条件下的1.66倍；尖轨降低值超限调整后，钢轨接触点的外移幅值为23.3 mm，与设计条件下一致。尖轨降低值超限时，转辙器处轮载过渡的起点发生后移现象，后移量约为6.4 m，与静力分析结果一致。由图9(b)可知：侧股行车时，开始阶段钢轨接触点不断外移，设计尖轨降低值条件下，钢轨接触点的外移幅值为16.8 mm；尖轨降低值超限调整前，钢轨接触点的外移幅值达到29.3 mm，为设计条件下的1.74倍；尖轨降低值超限调整后，钢轨接触点的外移幅值为9.1 mm，与设计条件相比偏小。尖轨降低值超限时，转辙器处轮载过渡的起点发生后移现象，后移量约为7.3 m，亦与静力分析结果一致。

尖轨降低值超限时，道岔转辙器轮载过渡起点的后移加大轮对通过转辙器时蛇行运动的距离和幅度，加剧轮对的摆动，最终会导致轮轨动力作用恶化，影响行车。尖轨降低值超限调整后，转辙器轮轨过渡的起点回复到设计条件的位置，减小了轮对通过道岔转辙器时的摆动，有利于车辆安全平稳地通过道岔转辙器。

3.2 车辆稳定

尖轨降低值设计条件、降低值超限调整前及调整后3种工况下计算的轮对横向位移的变化规律，见图10。

由图10(a)可知：直股行车时，设计尖轨降低条件下，轮对横向运动的幅值为5.1 mm；尖轨降低值超限调整前，轮对横向运动的幅值为11.3 mm，为设计条件下的2.2倍；尖轨降低值超限调整后，轮对横向运动的幅值为3.82 mm，较设计条件下有所减小。由图10(b)可知：侧股行车时，设计尖轨降低条件下，轮对横向运动的幅值为9.2 mm；尖轨降低值超限调整前，轮对横向运动的幅值为10.2 mm，相比设计条件略有增大；尖轨降低值超限调整后，轮对横向运动的幅值为9.0 mm，较设计条件下略有减小。

尖轨降低值设计条件、降低值超限调整前及调整后3种工况下计算的车体横向加速度的变化规律见图11。

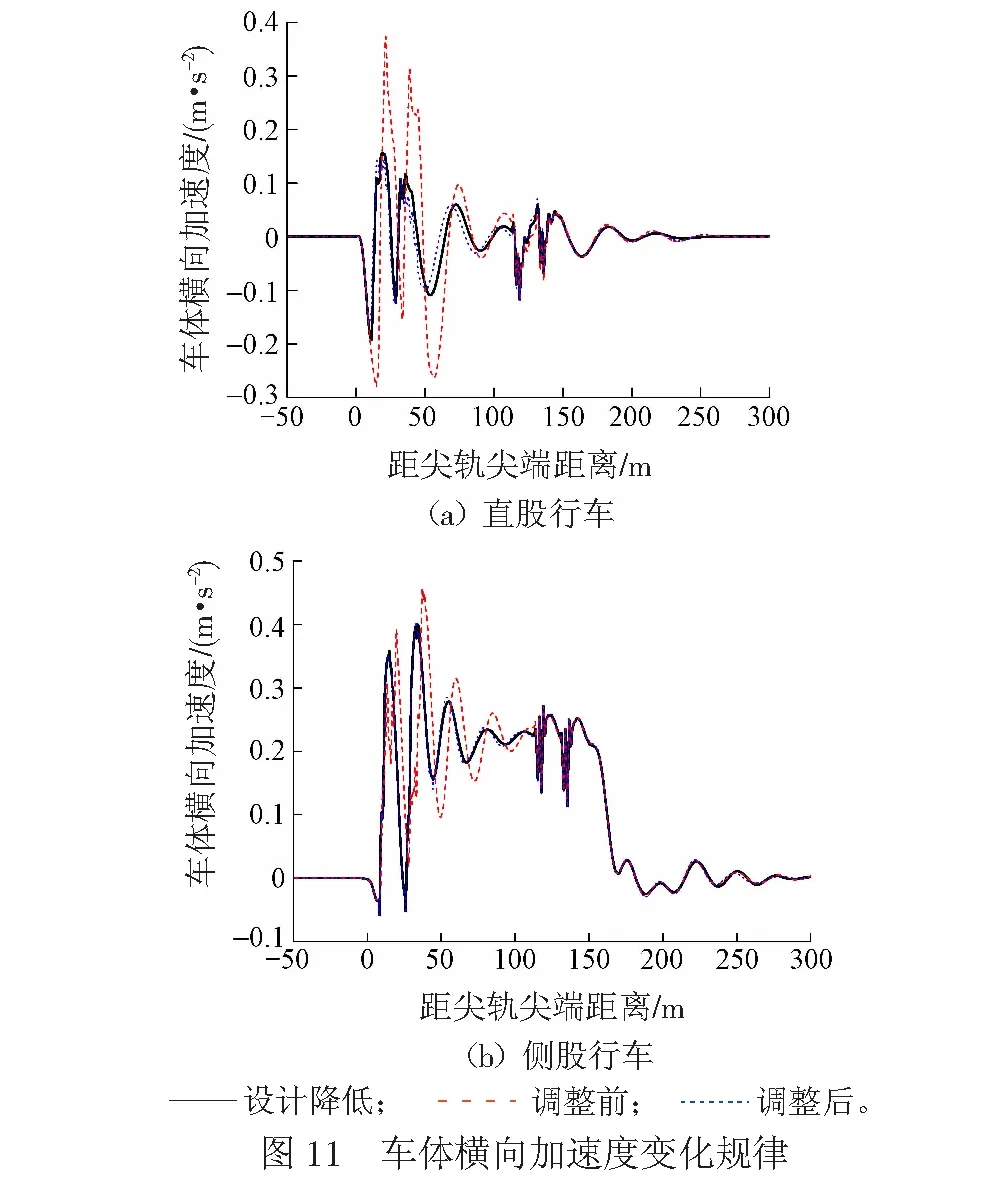
由图11(a)可知：直股行车时，设计尖轨降低条件下，车体横向加速度的幅值为0.193 m/s2；尖轨降低值超限调整前，车体横向加速度的幅值为0.374 m/s2，为设计条件下的1.9倍；尖轨降低值超限调整后，车体横向加速度的幅值为0.164 m/s2，相比设计条件下有所减小。由图11(b)可知：侧股行车时，设计尖轨降低条件下，车体横向加速度的幅值为0.400 m/s2；尖轨降低值超限调整前，车体横向加速度的幅值为0.457 m/s2，为设计条件下的1.2倍；尖轨降低值超限调整后，车体横向加速度的幅值为0.401 m/s2，与设计条件下的基本相同。

由直股行车时3种工况下轮对横向位移变化规律和车体横向加速度变化规律可知，与设计尖轨降低值条件相比，尖轨降低值超限工况下车辆通过道岔转辙器时，轮对的横向位移幅值和车体横向加速度幅值均显著增大，约为设计条件下的2倍，容易引起晃车现象，解释了现场车辆通过转辙器时存在的晃车现象。尖轨降低值调整后，车辆通过道岔转辙器时，轮对横向位移幅值和车体横向加速度幅值相比设计条件均有一定程度的减小，说明调整尖轨降低值有效。

3.3 轮轨动力附加力

尖轨降低值设计条件、降低值超限调整前及调整后3种工况下计算的轮轨横向和垂向动力附加力的变化规律见图11、图12。

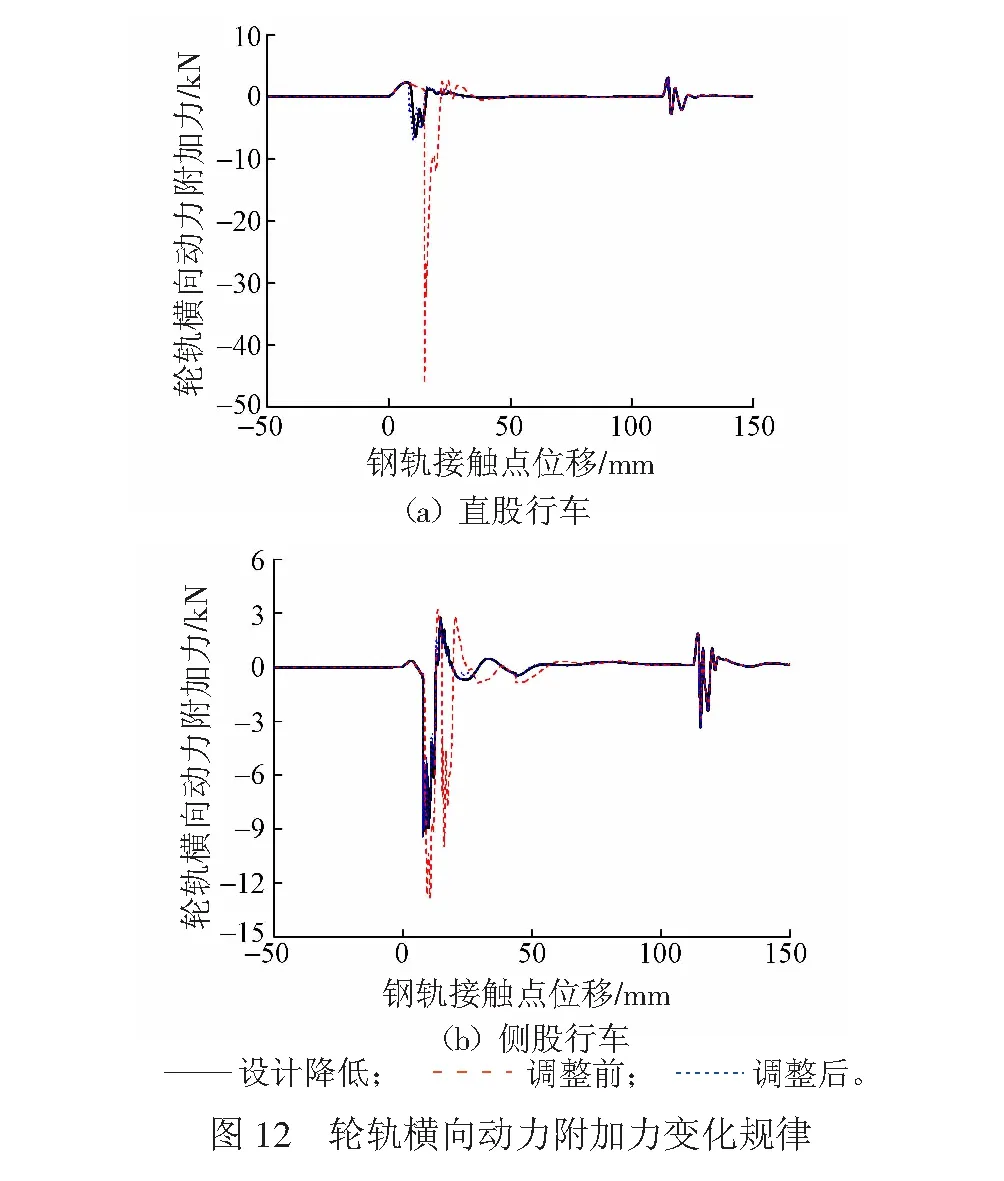
由图12(a)可知：直股行车时，尖轨降低值设计条件下，轮轨横向动力附加力幅值为6.29 kN；尖轨降低值超限调整前，轮轨横向动力附加力幅值为46.28 kN，为设计条件下的7倍；尖轨降低值超限调整后，轮轨横向动力附加力幅值为6.98 kN，较设计条件有所增大。由图12(b)可知：侧股行车时，尖轨降低值设计条件下，轮轨横向动力附加力幅值为9.06 kN；尖轨降低值超限调整前，轮轨横向动力附加力幅值为12.83 kN，为设计条件下的1.4倍；尖轨降低值超限调整后，轮轨横向动力附加力幅值为8.99 kN，较设计条件略有减小。

由图13(a)可知：直股行车时，尖轨降低值设计条件下，轮轨垂向动力附加力幅值为5.73 kN；尖轨降低值超限调整前，轮轨垂向动力附加力幅值为20.04 kN，为设计条件下的3.5倍；尖轨降低值超限调整后，轮轨垂向动力附加力幅值为10.98 kN，较设计条件有所增大。由图13(b)可知：股行车时，尖轨降低值设计条件下，轮轨垂向动力附加力幅值为16.97 kN；尖轨降低值超限调整前，轮轨垂向动力附加力幅值为9.51 kN，较设计条件有较大的减小；尖轨降低值超限调整后，轮轨垂向动力附加力幅值为16.75 kN，较设计条件略有减小。

由直股行车3种工况下轮轨动力附加力的变化规律可知：与尖轨降低值设计条件相比，尖轨降低值超限时轮轨动力附加力有显著的增大，尤其是横向动力附加力，增大幅度为7.0倍，垂向动力附加力的增大幅度达到3.5倍。尖轨降低值超限时，轮轨动力作用急剧恶化，加大转辙器处钢轨的伤损和磨耗速率，降低钢轨使用寿命。钢轨的伤损反过来加剧轮轨动力作用的恶化，形成恶性循环。尖轨降低值调整后，轮轨的动力附加力恢复到一个较小的水平，与设计条件相比则有所增大，说明调整尖轨降低值有效。

3.4 行车安全

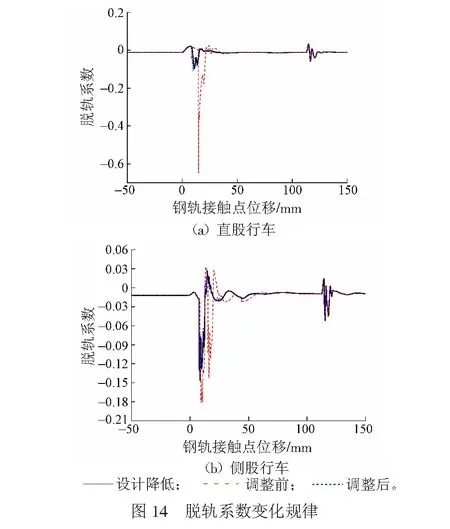
尖轨降低值设计条件、降低值超限调整前及调整后3种工况下计算的车轮脱轨系数的变化规律见图14。由图14(a)可知：直股行车时，尖轨降低值设计条件下，车轮的脱轨系数幅值为0.10；尖轨降低值超限调整前，车轮的脱轨系数幅值为0.65，是设计条件下的6.5倍；尖轨降低值超限调整后，车轮的脱轨系数幅值为0.11，相比设计条件有所增大。由图14(b)可知：侧股行车时，尖轨降低值设计条件下，车轮的脱轨系数幅值为0.15；尖轨降低值超限调整前，车轮的脱轨系数幅值为0.18，是设计条件下的1.2倍；尖轨降低值超限调整后，车轮的脱轨系数幅值为0.14，比设计条件的略有减小。

理论仿真尖轨降低值设计条件、降低值超限调整前及调整后3种工况下车轮减载率的变化规律见图15。由图15(a)可知：直股行车时，尖轨降低值设计条件下，车轮的减载率幅值为0.06；尖轨降低值超限调整前，车轮的减载率幅值为0.08，与设计条件的相差不大；尖轨降低值超限调整后，车轮的减载率幅值为0.14，较前两种工况均有所增大，但数值相差不大。由图15(b)可知：股行车时，设计尖轨降低值条件下，车轮的减载率幅值为0.05；尖轨降低值超限调整前，车轮的减载率幅值为0.03，与设计条件比较小但相差不大；尖轨降低值超限调整后，车轮的减载率幅值为0.04，与前两种工况的相差不大。

由直股行车3种工况下车轮脱轨系数和减载率的变化规律可知：相比尖轨降低值设计条件，尖轨降低值超限时，车轮脱轨系数显著增大，脱轨系数达到0.65，已十分接近安全限值0.8，约为设计条件下的6.5倍;车轮减载率变化不大，说明尖轨降低值超限时，车辆通过转辙器时，行车安全出现很大程度的恶化，严重时可能危及行车安全；尖轨降低值调整后，车轮脱轨系数与设计条件下相比变化不大，车轮减载率有所增大，说明调整尖轨降低值有效。

比较动车组车辆直股行车和侧股行车时道岔转辙器的动力响应，发现直股行车时尖轨降低值超限对道岔转辙器动力特性的影响大于侧股行车时的。主要原因有两点：①动车组车辆直股行车的速度是295 km/h，远大于侧股行车的速度120 km/h；②道岔内不设置超高，因此动车组车辆侧股行车时，由于道岔曲线线形的影响，离心运动在车辆的运动过程中起主要作用，此时尖轨降低值超限对道岔转辙器动力响应带来的影响不明显。

4 结论

本文针对42号高速道岔尖轨降低值设计条件、超限调整前及调整后3种工况下，研究车辆通过时对道岔转辙器动力特性的影响。主要结论如下：

(1) 与设计条件相比，尖轨降低值超限时道岔转辙器轮载过渡段起点后移，加大了轮对通过转辙器时蛇行运动的距离和幅度，加剧了轮对的摆动，最终导致轮轨动力作用恶化，影响行车。

(2) 直股行车时，与设计条件相比尖轨降低值超限、车辆通过道岔转辙器处时，轮对横向位移和车体横向加速度均显著增大，约为设计条件下的2倍，容易引起晃车现象，解释了现场车辆通过该道岔转辙器时存在的晃车现象。

(3) 直股行车时，与设计条件相比尖轨降低值超限时轮轨动力附加力显著增大，尤其是横向动力附加力增大幅度为7.0倍，垂向动力附加力的增大幅度约为3.5倍，轮轨动力作用的急剧增大，加大转辙器处钢轨的伤损速率，降低钢轨使用寿命，钢轨的伤损反过来加剧轮轨动力作用的恶化，形成恶性循环。

(4) 直股行车时，与设计条件相比尖轨降低值超限时车轮脱轨系数显著增大，脱轨系数幅值达到0.65，十分接近安全限值0.8，约为设计条件下的6.5倍，车轮减载率变化不大。车辆通过转辙器时，行车安全出现很大程度的恶化，严重时可能危及行车安全。

(5) 尖轨降低值出现超限时，道岔转辙器的动力特性出现很大程度的恶化。调整后的道岔转辙器动力特性与设计条件相差不大，说明尖轨降低值调整有效。

参考文献：

[1〗 DUKKIPATI R V. Lateral Stability Analysis of a Railway Truck on Roller Rig[J〗. Mechanism and Machine Theory, 2001,36(2):189-204.

[2〗 王开云，刘鹏飞.车辆蛇形运动状态下重载铁路轮轨系统振动特性[J〗.工程力学，2012，29(1)：235-239.

WANG Kaiyun, LIU Pengfei. Characteristics of Dynamic Interaction Between Wheel and Rail due to the Hunting Montion on Heavy-haul Railway, 2012,29(1):235-239.

[3〗 王平.道岔转辙器部分的力学特性分析[J〗.铁道学报，2000，22(1)：79-82.

WANG Ping. Analysis of Mechanical Characteristic for Switch Proper of Turnout[J〗. Journal of The China Railway Society, 2000,22(1):79-82.

[4〗 王平.高速铁路道岔设计理论与实践[M〗.成都：西南交通大学出版社，2011：209-231.

[5〗 蔡小培，王平，李成辉.转辙器轨距加宽对高速道岔动力特性的影响[J〗.铁道科学与工程学报，2008，5(4)：1-6.

CAI Xiaopei, WANG Ping, LI Chenghui. Effect of Gauge Widening of Switch on Dynamic Characteristics of High-speed Turnout[J〗. Journal of Railway Science and Engineering, 2008,5(4):1-6.

[6〗 刘哲，王平，陈嵘，等.道岔动力参数设计法及其在转辙器设计中的应用[J〗.西南交通大学学报，2012，47(4)：611-617.

LIU Zhe, WANG Ping, CHEN Rong,et al. Dynamic Parameters Design Method for Turnout and Its Application in Switch Design[J〗. Journal of Southwest Jiaotong University,2012,47(4):611-617.

[7〗 中华人民共和国铁道部.TB/T3302—2003高速铁路无砟轨道岔铺设技术条件[S〗.北京：中国铁道出版社，2003.

[8〗 曹阳.道岔平面线型动力分析及其设计方法研究[D〗.成都：西南交通大学，2013：33-64.

[9〗 陈小平.高速道岔轨道刚度理论及应用研究[D〗.成都: 西南交通大学，2008：36-46.

[10〗 陈果.车辆-轨道耦合系统随机振动分析[D〗.成都：西南交通大学，2000：100-104.

[11〗 王开文.车轮接触点迹线及轮轨接触几何参数的计算[J〗.西南交通大学学报，1984，19(1)：89-98.

WANG Kaiwen. The Track of Wheel Contact Points and the Calculation of Wheel/Rail Geometric Contact Parameters[J〗. Journal of Southwest Jiaotong University,1984,19(1):89-98.

[12〗 严隽髦.具有任意轮廓形状的轮轨空间几何约束的研究[J〗.西南交通大学学报，1983，18(3)：40-48.

YAN Juanmao. A Study on Wheel/Rail Spatial Geometric Constrains for Arbitrary Wheel and Rail Profiles[J〗. Journal of Southwest Jiaotong University, 1983,18(3):40-48.