单一裂缝条带示踪剂产出模型及其参数敏感性分析

景成, 蒲春生, 何延龙, 谷潇雨, 刘洪志, 崔淑霞

(中国石油大学(华东)石油工程学院, 山东 青岛 266580)

0 引 言

井间示踪监测技术作为井间动态监测技术的重要组成部分,已广泛运用于确定井间连通性、高渗通道和非均质性等方面[1-8]。定量化解释方法有解析法、数值法和半解析法,其中解析法和数值法都是把油藏处理为由均质、互不连通的一些层组成的“千层饼”,半解析法则是利用流线法将数值计算的压力分布与解析法计算的示踪剂浓度联系起来,实现对示踪剂产出曲线的解释[8-12]。对于裂缝广泛发育的特低渗透油藏,大量的井间化学示踪矿场实践结果表明,见剂井的见剂时间和出现峰值浓度时间普遍很快,有的不足一个月示踪剂的回采率就可高达90%以上,可见裂缝是注入水流动的主要通道,显然解析法与数值法的“千层饼”模型以及半解析法中计算压力分布的黑油模型对于裂缝性特低渗透油藏示踪剂解释是不适用的[8-13]。

对于这类特殊油藏的井间示踪剂解释模型仍沿用上述3种模型笼统的解释,利用不同方法确定出的高渗透裂缝通道的参数差异较大,且参数的可参考性和可靠性备受质疑,仅可进行定性分析[6-13]。对该类油藏的精细开发,精确的油层信息(特别是裂缝信息)是后期调整挖潜的重要前提条件。针对裂缝性特低渗透油藏的井间示踪剂解释模型国内外尚未见到。本文通过建立单一裂缝条带分布的物理模型,从一维对流扩散方程出发,将单一裂缝条带等效为符合Hagen-Poiseaille方程的流管束,建立了单一裂缝条带示踪剂产出数学模型,并对该模型中主要参数的敏感性进行分析,研究成果可为建立裂缝性特低渗透油藏的示踪剂解释模型提供理论基础。

1 基本假设和物理模型

根据裂缝性特低渗透油藏水驱开发特征,对注入水及示踪剂及其在该类油藏中的运动作以下基本假设:①注入水为连续流动的不可压缩流体;②示踪剂在注入过程中类似于水,对示踪剂运动的分析相当于对水运动的分析;③忽略流体重力及毛细管力,在裂缝中示踪剂与注入水为流度比等于1的活塞式驱替;④忽略示踪剂纬向弥散和分子扩散的影响,示踪剂不吸附到岩石壁面上;⑤忽略基质与裂缝的渗吸置换,流体仅在裂缝中流动;⑥流体在裂缝中的流动符合Hagen-Poiseaille方程。

以五点法1/4井网为例,发育一条贯通于注水井与采油井之间的裂缝条带,利用等效流管法可把该裂缝条带等效为由n个长度为s、当量直径为D的流管组成的流管束(见图1),示踪剂可以看成是在一条裂缝条带中的n个流管中流动。该物理模型对应的示踪剂产出曲线为单峰型(见图2)。

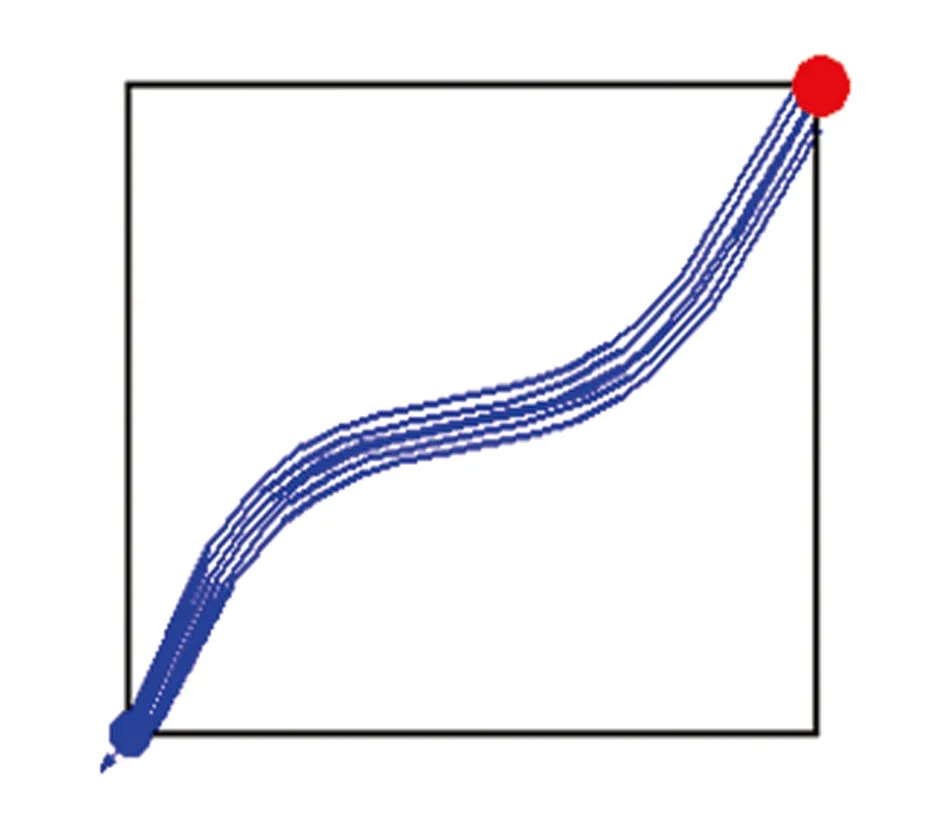
图1 单一裂缝条带等效流管束模型

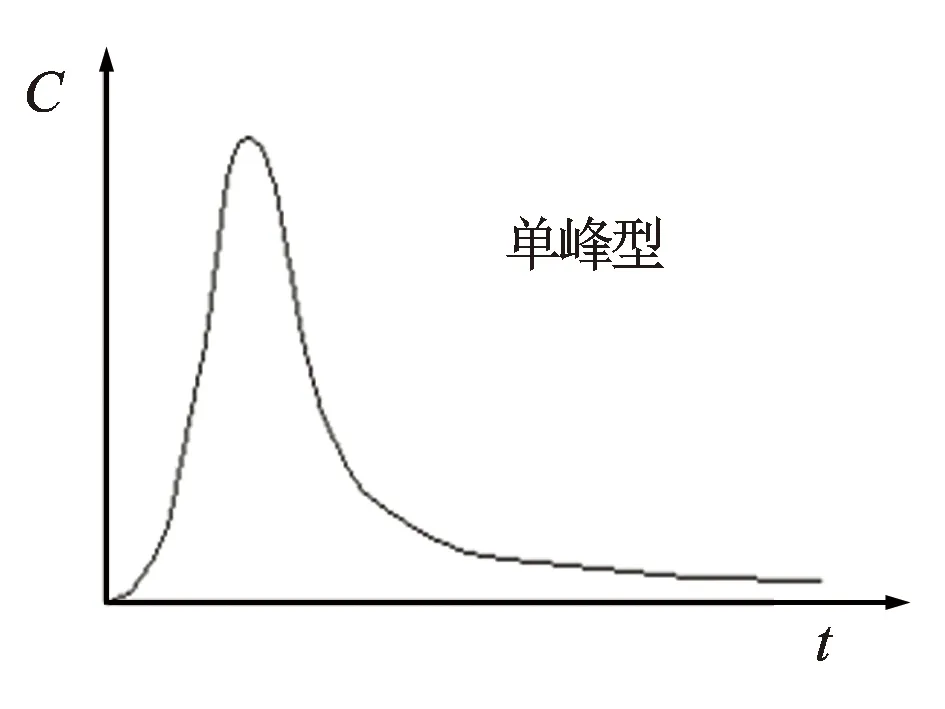
图2 单峰型示踪剂产出曲线示意图

2 单一裂缝条带示踪剂产出数学模型

2.1 示踪剂在光滑圆管定浓度边界条件下的浓度分布模型

设有一半无限长的光滑圆管,一维稳定流动,平均流速为v,其一端为定浓度边界,求其浓度C分布(见图3)。

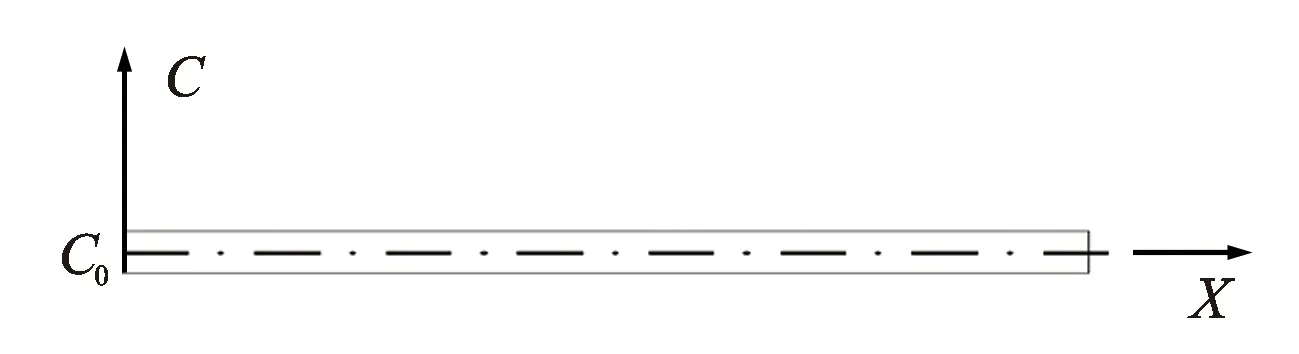
图3 一维光滑圆管中一端为定浓度边界问题

该问题的数学模型可描述为

(1)

C(x,0)=0

C(0,t)=C0,t>0

C(∞,t)=0,t>0

式中,k为水动力弥散系数;C0为初始浓度。

经求解,得到光滑圆管定浓度边界条件下的示踪剂浓度分布方程的解析解

(2)

当k/v<<0.005时,式(2)的第2项可以忽略不计,可以将之简化为

(3)

2.2 示踪剂段塞在光滑圆管中的浓度产出模型

当单一小段塞示踪剂注入管中时,其长度远远小于圆管长度,可以由式(3)改型得到

(4)

如图4所示,长度为L的光滑圆管中,示踪剂在其中的浓度,都可以由类似式(4)给出

(5)

当s=L时,式(5)即为示踪剂在光滑圆管中的浓度产出方程。示踪剂在光滑圆管中的流动可以看成是在流管中的流动,因此式(5)即为示踪剂在任一流管中的浓度方程。

图4 光滑圆管中示踪剂段塞的位置

2.3 单一裂缝条带任意的第i条流管中的示踪剂浓度产出方程

利用式(5),任一流管注入的示踪剂段塞体积为V段i=fjV段/n,其中,fj为注入水向油井j的分配系数,可由各个油井测得的示踪剂产出量占总的示踪剂注入量的比值得到。

(6)

σ2=2kt=2αvt

(7)

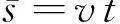
(8)

(9)

将式(6)、式(7)、式(8)和式(9)都代入式(5),得

(10)

2.4 单一裂缝条带所有流管示踪剂产出浓度在生产井的叠加

最终生产井j测得的示踪剂浓度为

(11)

经量纲分析及单位换算,得到

(12)

式中,C为示踪剂产出浓度,mg/L;C0为示踪剂初始注入浓度,mg/L;V段为示踪剂初始注入量,m3;fj为向油井j的注入水分配系数,f;n为等效的流管数,个;D为流管的当量直径,μm;α为水动力弥散度,m;Q为平均日注入量,m3/d;t为示踪剂注入天数,d;s为流管的等效长度,m。

式(12)中,流管当量直径D可转化为渗透率K的表达式,当把流体在流管中的运动看作是达西流时,由达西定律和Hagen-Poiseuille方程可推导出单一流管的渗透率KT与当量直径D的关系为

(13)

又可得到每条裂缝条带的渗透率KF与单一流管的渗透率KT相等,均可由其对应的流管当量直径D求得。实际应用中,该数学模型中的参数V段、C0、fj等是已知的,通过现场示踪剂产出曲线反演拟合,可得到流管束(裂缝条带)参数n、D、KF、α、s和Δp,采用这些参数利用Hagen-Poiseuille公式可以计算出井网任一生产注采压差Δp1,把Δp1与利用平均注入压力及生产井动液面估算的压差Δp2相比较,可进一步验证示踪剂解释的准确性。

3 单一裂缝条带示踪剂产出数学模型参数敏感性分析

对于单一裂缝条带示踪剂产出数学模型中的参数,结合现场,先选取V段=10 m3,fj=0.25,应用Matlab软件计算并作图,分别对n、D、α、s、Δp参数进行变量分析。

(1) 流管数n对单一裂缝条带示踪剂响应曲线特征的影响。选取s=150 m,D=8 μm,α=0.5 m。同时选取Q=10 m3/d,此时计算出生产压差Δp=4.32 MPa。对于n,给定变化范围为1×1010～1.8×1010,步长为0.2×1010,作图得示踪剂标准浓度C/C0和t的关系曲线(见图5)。由图5可以看出,当流管数n变大时,示踪剂突破时间延后,曲线向右移动,同时突破时峰值减小,单峰变缓,整体油井示踪剂见剂时间变长。裂缝的等效流管数n变大,每一根流管中的流量Q就会变小,注入流体的平均流速变小,突破时间增大;而每个流管中浓度Ci也会随之减小,造成突破峰值变小。

图5 流管数n对示踪剂产出浓度的影响

(2) 流管长度s对单一裂缝条带示踪剂响应曲线特征的影响。选取n=1×1010,D=8 μm,α=0.5 m,Δp=4.32 MPa。对于s,给定变化范围为150～230 m,步长为20 m,作图得示踪剂标准浓度C/C0和t的关系曲线(见图6)。图6表明,当流管长度(裂缝长度)增长时,示踪剂突破时间延后,曲线向右移动,同时突破时峰值减小。流管等效长度s变大,在流管中的流量Q和注入流体的平均流速不变的情况下,突破时间就会增大;又由于流管变长,示踪剂在流管中流动的时间变长,弥散程度也就越大,从而导致突破时示踪剂段塞的浓度降低,峰值下降。

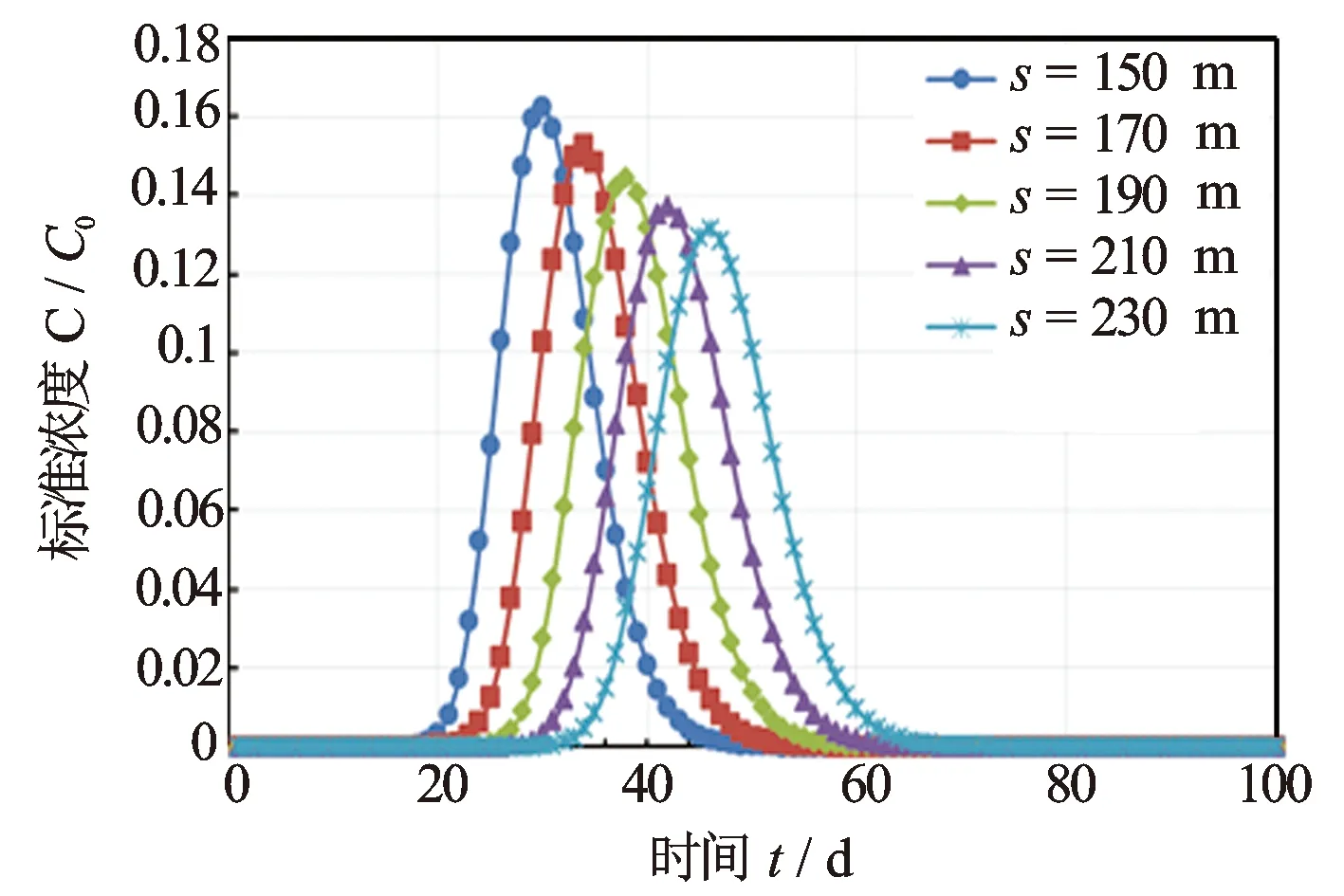
图6 流管长度s对示踪剂产出浓度的影响

(3) 流管当量直径D对单一裂缝条带示踪剂响应曲线特征的影响。选取n=1×1010,s=150 m,α=0.5 m,Δp=4.32 MPa。对于D,给定变化范围为到8～10 μm,步长为0.5 μm,作图得示踪剂标准浓度C/C0和t的关系曲线(见图7)。图7表明,随着流管的当量直径D变大,示踪剂突破时间延后,曲线向右移动,同时突破时峰值减小,单峰变宽变缓,整体油井示踪剂见剂时间变长。流管当量直径D变大,在整个井组注入量Q不变的情况下,单个流管中的平均流速v减小,突破时间就会增大,从而弥散程度也就越大,导致突破时示踪剂段塞的浓度降低,峰值下降。

图7 当量直径D对示踪剂产出浓度的影响

(4) 注采压差Δp对单一裂缝条带示踪剂响应曲线特征的影响。选取n=1×1010,s=150 m,D=8 μm,α=0.5 m。对于Δp,将Q给定变化范围为4～12 m3/d,步长为2 m3/d,则Δp的对应变化范围为1.72～5.18 MPa,作图得示踪剂标准浓度C/C0和t的关系曲线(见图8)。图8表明,随着生产注采压差Δp(即注入量Q)变大,示踪剂突破时间提前,曲线向左移动,但不影响突破时的峰值大小,单峰变窄变陡,整体油井示踪剂见剂时间变短。原因是注入量Q增大,流管中示踪剂的平均速度vi也增大,从而突破时间减小。

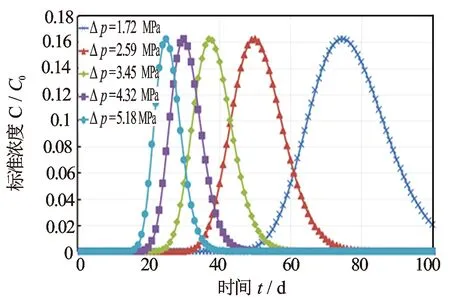
图8 注采压差Δp对示踪剂产出浓度的影响

4 结 论

(1) 通过建立单一裂缝条带分布的物理模型,从一维对流扩散方程出发,将单一裂缝条带等效为符合Hagen-Poiseaille方程的流管束,将宏观生产信息与微观裂缝信息有机结合起来,建立了单一裂缝条带示踪剂产出数学模型。

(2) 对单一裂缝条带示踪剂产出数学模型中主要参数的敏感性进行了分析。结果表明,流管个数、流管长度和当量直径与示踪剂峰值浓度呈负相关,与峰值突破时间呈正相关,随着流管个数、流管长度和当量直径的增大示踪剂浓度曲线形态变宽;注采压差不改变峰值浓度值,与峰值突破时间呈负相关,随着注采压差的增大示踪剂浓度曲线形态变窄。研究成果可为建立裂缝性特低渗透油藏的示踪剂解释模型提供理论基础。

参考文献:

[1] Brigham W E, Smith D H. Prediction of Tracer Behavior in Five-spots [C]∥Paper SPE 1130, Oct, 1965.

[2] Yuen D L, Brigham W E, Cindo-Ley H. Analysis of Five-spots Tracer Test to Determine Reservoir Layeting [R]. DOE Report SAW 1265-8, Feb, 1979.

[3] Brigham W E, Maghsood Abbaszadeh Dehghani. Tracer Testing for Reservoir Description [J]. JPT, May, 1987.

[4] Maghsood Abbaszadeh Dehaghani, Brigham W E. Analysis of Unit Mobility Ratio Well-to-Well Tracer Flow to Determine Reservoir Heterogeneity [C]∥ DOE/SF/11564-1, 1983.2.

[5] Naji Saad C T Kalkomey. Ranking Geostatistical Models Using Tracer Production Data [C]∥SPE 35494, 16-17, April, 1996.

[6] 陈月明, 姜汉桥, 李淑霞. 井间示踪剂监测技术在油藏非均质性描述中的应用 [J]. 石油大学学报: 自然科学版, 1994, 18(A00): 1-7.

[7] 张钊, 陈明强, 高永利. 应用示踪技术评价低渗透油藏油水井间连通关系 [J]. 西安石油大学学报: 自然科学版, 2006, 21(3): 48-51.

[8] 张毅, 姜瑞忠. 井间示踪剂分析技术 [J]. 石油大学学报: 自然科学版, 2001, 25(2): 76-78.

[9] 李淑霞, 陈月明. 示踪剂产出曲线的形态特征 [J]. 油气地质与采收率, 2002, 9(2): 66-67.

[10] 于金彪, 宋道万, 秦学杰, 等. 井间示踪剂解释模型研究 [J]. 油气地质与采收率, 2003, 10(6): 42-44.

[11] 张勇. 基于流线模拟的井间示踪剂解释方法研究 [D]. 成都: 西南石油学院, 2003.

[12] 刘同敬, 姜汉桥, 李秀生, 等. 井间示踪剂测试半解析方法体系数学模型 [J]. 石油学报, 2007, 28(5): 118-123.

[13] 冯宝峻, 杜兴家, 李林. 油田井间示踪技术译文集 [M]. 北京: 石油工业出版社, 1994.