电磁学与电动力学中的磁单极
—Ⅴ
陈 丽王 青(大理大学工程学院,云南大理 67003;清华大学物理系,北京 00084)
电磁学与电动力学中的磁单极
—Ⅴ
陈 丽1王 青2
(1大理大学工程学院,云南大理 671003;2清华大学物理系,北京 100084)
摘 要作为本系列5篇文章的最后一篇,作者在电磁学和电动力学框架内用尽量科普的方式对比前4篇文章介绍一个磁单极很不奇特的性质.本文主要研究用小电流圈定义的磁偶极子和用正负磁单极对定义的磁偶极子的差别.文章仔细讨论一个在2012年曾在业界引起很多争议的由一个点电荷和一个磁偶极子构成的体系的可能的现象,并展示对这个体系,由正负磁单极对构成的磁偶极子比由电流圈构成的磁偶极子要简单和平庸许多.
关键词磁偶极子;电流圈;正反磁单极子对
本文是在电磁学和电动力学中讲解磁单极奇妙性质的最后一篇文章,也是在原来计划的4篇文章基础上增补的一篇.在前4篇文章[1-4]中分别介绍了磁单极在角动量方面的角色和作用,狄拉克磁单极及其与规范变换的关系,磁单极在作用量中的作用,磁单极在磁电介质中的作用.可以换种角度来对前面文章中出现的各种磁单极子系统进行分类,首先单个的狄拉克磁单极是我们第2篇文章[2]主要讨论的内容,它通过一系列正负磁单极对构造的磁偶极子从某个场点串联起来连到无穷远在场点形成单个的狄拉克磁单极.这篇文章提示我们即使研究单个磁单极,应该在其中加入一些新的物体(这里是一系列正负号相间的磁单极串);通过观察它们之间相互作用或它们的联合行为来展示磁单极的奇特效应.对单个磁单极系统可加入的另一种最简单物体,就是点电荷,如果这个新加入的点电荷与磁单极之间相互分离并且相互都不受其他外力而运动,就会引出我们在第1篇文章[1]站在磁单极上观察运动的电荷进而讨论的系统角动量问题;而如果这个新加入的点电荷与磁单极之间相互分离并且受外力而被约束在某个区域运动,就引发我们在第3篇文章[3]站在位于球心的磁单极上观察被约束在单位球面上的点电荷运动进而讨论所导致的作用量不存在问题;如果这个新加入的点电荷和磁单极不分离而是结合在一起,就导致我们在第4篇文章[4]在磁电介质中讨论的双荷子.在这4篇文章中,我们在原始的磁单极上要么额外加进负号磁单极形成磁偶极子要么加进点电荷,自然一个更进一步的扩展系统是考虑既加进负号磁单极又加进点电荷,这就是本篇文章所要关注的新体系.在第2篇文章[2]所涉及的磁偶极子描述中原始的出发点是正负磁单极子组成的系统,但实际上却是以一系列电流圈构造的磁偶极子串——也就是螺线管来实行计算,这自然提出以正负磁单极子对构造的磁偶极子和以电流圈构造的磁偶极子是否完全一样的问题,这是本文所关注的重点.以往这些文章都给出磁单极在特定电磁学和电动力学系统中所呈现出的非常有别于纯电荷电流体系的现象,磁单极的出场总是展示出另类特别的特点.作为磁单极系列的收官文章,我们为反衬前4篇文章中磁单极的奇怪与非平庸,在本文中反其道而行之,证明磁单极也可能只产生极平庸的现象和结果,反而是普通的电荷电流会造就不平庸和奇怪的现象.以下先在第1节把磁偶极子的两种不同定义的问题提出来,引进点电荷与磁偶极子的系统并进行讨论;然后在第2节介绍2012年业界在点电荷与磁偶极子系统中对狭义相对论和电动力学可能冲突的讨论,并讨论它与我们介绍的磁偶极子两种不同定义之间的关联;最后在第3节对点电荷与磁偶极子的系统中磁偶极子是延展的情形做详细的计算,进一步地验证第2节的结论.
1 磁偶极子的定义
这个标题看起来好似十分平庸,其实不然.学过电磁学的人都知道磁偶极子.它的标准定义是一个截面积S(矢量方向代表面积的法向)电流强度I的小电流圈体系,这个电流圈的面积趋于零但电流强度趋于无穷大,保持两者乘积固定.这个体系(假设位于坐标原点)的矢量势A电流圈为
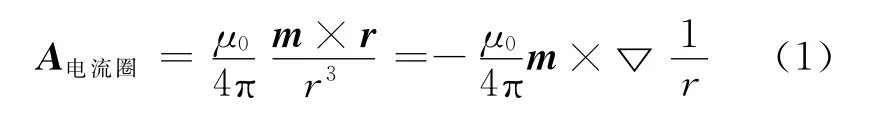
其中r是磁偶极子到场点的距离,m是磁偶极子的磁偶极矩,它可以写成

这里j是磁偶极子的电流密度.此磁偶极子所产生的磁感应强度B电流圈为
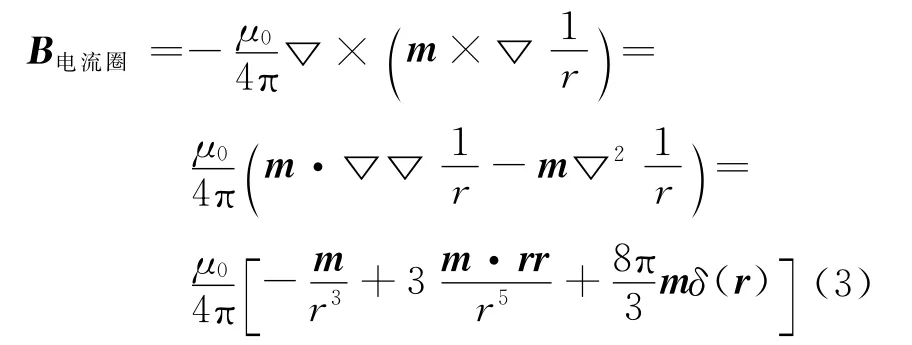
注意式(3)中最后的正比于δ函数的项通常是被忽略掉的,因为通常所讨论的磁偶极子的场都不在r=0处,这时最后一项恒为零.注意按照安培环路定理,此磁感应强度对应的电流密度若用磁偶极矩m表达则为也就是磁偶极子中存在一个电流源.如果用磁化强度M描写的话,由j=×M我们得到M=mδ(r).
目前这个磁偶极子的电流圈定义实际上和其所叫的名称是不一致的,因为名称原本指的是一对相互反号无穷靠近的磁单极.只是因为在现实世界没看到磁单极,而人们又发现电流圈的磁感应强度在r≠0处和一对相互反号的无穷靠近的磁单极的磁感应强度完全一样,因此用电流圈代替描写真正的磁偶极子.那原本的磁偶极子真可以完全等价于电流圈吗?以下我们先设法直接计算最原始的一对相互反号无穷靠近的磁单极的磁感应强度.在一定的磁荷单位选择下,一个磁荷为g的磁单极的磁感应强度为(其中μ0是真空的磁导率),因此此磁单极对应的磁标势为把它和电量为q的点电荷的标量势(其中ε0是真空的介电常数)进行对比,发现我们磁荷单位的选择使得磁荷与电荷的对应关系为:以此对应关系,从电偶极矩为p=ql(其中正反电荷之间的距离l→0,q→∞但维持电偶极矩p固定)的电偶极子的标量势为出发,我们利用对应关系得到磁偶极矩为

正负磁单极子之间的距离l→0,g→∞但维持磁偶极矩m固定的正负磁单极构成的原始磁偶极子的磁标势为

而它对应的磁感应强度B正负磁单极为

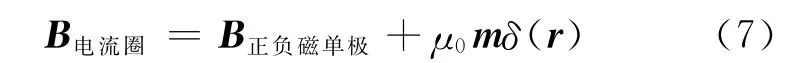
其中式(7)最后的δ函数项贡献的是式(3)和式(6)所差别的纯电流源项,或者用前面讨论的此纯电流源贡献的磁化强度M=mδ(r)来描写即为若有办法从实验上区分出这种差别,我们就能真正鉴别在物理中实际碰到的磁偶极子到底属于哪种!这对寻找磁单极具有重大意义,因为即使找不到单独存在的磁单极,若能发现由正负磁单极对构成的磁偶极子,也是磁单极存在的重要证据.
为看出两种不同的磁偶极子定义可能的物理效应,我们考察在离磁偶极子d处放置一个电量为q的静止点电荷,d的方向由磁偶极子指向点电荷(注意这和我们磁单极系列文章第4篇[4]讨论的点电荷与一个磁单极构成的双荷子体系是不一样的,现在一是电荷与磁单极之间的距离可以是有限的,二是现在是两个相互反号的磁单极而不是单个磁单极.如不顾及距离有限而硬要与本系列文章第4篇[4]比较则相当于考虑两个相互反号的双荷子并在一起).我们关心点电荷与磁偶极子之间的相互作用能动量.在目前的静止系,相互作用的能量为零W静止=0(若不为零则需要有非此系统内点电荷产生的外电场或非此系统内磁偶极子产生的外磁场);但由于点电荷提供电场,磁偶极子提供磁场,这样一个既有电场又有磁场的体系应该具有相互作用的电磁动量P静止(这时点电荷和磁偶极子分别都具有无穷大的自作用的能量,但不具有自作用的动量).这对磁偶极子是由电流圈定义的情形来说确是如此,但对以正反磁单极对定义的磁偶极子来说,却不是这样.理由很简单,对正磁单极和点电荷联合产生的相互作用动量与负磁单极和点电荷联合产生的相互作用动量由于正反磁单极无穷靠近正好大小相等符号相反因而相互抵消为零.因此这样一个体系的电磁动量的取值依赖于磁偶极子的定义,特别对正负磁单极对定义的磁偶极子正好为零P正负磁单极,静止=0.对这个体系中的磁偶极子是由正负磁单极对定义的情形,由于在静止系的相互作用能动量都为零,因此依照洛伦兹变换,我们可以推出在任意匀速运动系下相互作用能动量都为零.

从这个结果看,由磁单极子构造的这个体系在相互作用能动量的意义上是最简单和平庸的.这与前4篇文章[1-4]中磁单极总是出风头的情形正好形成鲜明的反差,这里磁单极偃旗息鼓甘做低调平庸的角色.为了对比和以后的讨论,以下我们先利用式(7)和式(6)把磁偶极子是电流圈时静止系的电磁动量P电流圈,静止计算出来,

在整个体系以速度瓫运动的体系中,通过洛伦兹变换,我们得到
式(8)与式(10)、式(11)比较形成鲜明的反差,似乎通过观察体系的能动量既能鉴别磁偶极子是磁单极对还是电流圈构成的.然而这种反差真能有可观察的效应吗?
2 电动力学与狭义相对论冲突吗?
狭义相对论诞生于电动力学,它怎么能与它的母亲发生冲突呢?这事还真的貌似发生了,就发生在上节讨论的点电荷与磁偶极子系统中,它在2012年曾在业界曾引起了一个不小的波澜.事件过程如下:2012年5月7日,美国物理学会的著名杂志《物理评论快报》发表了美国Arizona大学光学数据储存中心主任、光学科学学院教授Masud Mansuripur撰写的题为“洛伦兹力的麻烦:与狭义相对论和动量守恒不协调”的文章[5],文章提出我们在电磁学和电动力学所熟知的洛伦兹力与狭义相对论的洛伦兹变换及动量守恒在某些地方会发生冲突.而在《物理评论快报》上文章还没正式发表出来之前,在4月27日发表的《SCIENCE》杂志上的新闻和分析版就已经有人发表了题为“教科书上的电动力学可能会与狭义相对论冲突”的介绍和评论这项工作的文章[6].在文中作者用图1直观而简洁地说明了冲突的所在之处:
图1(a)是一条通有电流向右流动(在其上电子反向向左运动)的导线,它在周围会产生磁场,这时导线上任何一处的电荷密度都为零.导线旁边有一个带正电的点电荷沿电流方向向右运动,它因导线上电流产生的磁场的作用而受指向导线的洛伦兹力(来自磁场).
图1(b)是站在点电荷静止的参考系(磁场对点电荷不会贡献洛伦兹力)中看(a).这时导线上原本在(a)中静止带正电的空穴开始运动,而导线上原本在(a)中反电流方向向左运动的电子运动速率也会变化,通过洛伦兹变换可以知道在(a)中导线中正好在带电方面相互抵消的空穴密度和电子密度在(b)中不再相互抵消(因为空穴是从静止变到运动,而电子是从运动变到运动或极端的情形可以从运动变到静止),因而在导线上产生了净剩的纯负电荷,它所产生的电场导致导线外静止的点电荷受到指向导线的洛伦兹力(来自电场).
图1(c)是一个带正电的静止点电荷和一个静止的被认为是一系列的电流圈构成的(也就是螺线管)磁铁体系.点电荷和磁铁相互之间不受力,也没有力矩.

图1 文献[6]中给出的说明电动力学可能会与狭义相对论冲突的示意图
图1(d)是出现冲突的情形.观察者不动,点电荷和磁铁都同时向右运动,如(b)所示原本无净电荷密度的电流线在运动后会遗留下净电荷密度,考虑到磁铁就是一系列电流圈,计及运动方向会导致磁铁两边分别出现不为零的正反电荷密度,因而形成电偶极子.此电偶极子会因其正反电荷的受力距离矢量不同而受到点电荷电场所施加的力矩,因而会产生旋转.这显然与(c)给出的物理图像相互冲突!为了解决此问题消掉这个不该出现的力矩Mansuripur提出应该修改洛伦兹力公式,并做了十分复杂的讨论.
看到这些报道,在当年清华物理系的电动力学课上作者即给学生介绍了这个问题,作者系里上普通物理电磁学课的老师据说也做了类似的介绍.当时清华物理系的一些学习比较好的同学就开始在老师的建议下自己琢磨如何解决此问题.其中的一位叫吴宇恺的同学在5月19日还特别在系里做了题为“Lorentz力公式是否需要修正”的报告,指出洛伦兹力实际上是不需要进行修正的.据说他还把结果写成文章投稿到《物理评论快报》上,遗憾的是杂志拒绝发表他的文章.但杂志确在一年后集中发表了一系列对Mansuripur结果进行批评的评论文章[7-10]及Mansuripur对这些评论给予的摘要回复[11].Mansuripur的详细回复发表在文献[12]上.2015年本文作者在清华物理系给学生上课讨论费曼第二册书的内容,当谈到图1的上右图中涉及的运动导线上电荷密度为什么不为零的计算时,把这段业界的风波做了简要介绍,并作为一个课题留给学生课后研究.有四位同学自告奋勇组织课后讨论,他们研究了所有能找到的相关材料包括前面提到的学长吴宇恺报告的PPT,然后在2015年5月13日的课堂上先后由童鑫熠、谢天佑、徐集思和刘陆川共用三节课的时间把前人的工作及他们的理解、看法和解决方案进行了报告.课上大家进行了激烈的讨论,正是因为此次报告的刺激才激发作者写作此文.作者对文献中和同学们提出的解决这个问题的各种方法和角度进行整理归纳,与大家进行分享.由于电流圈可以有无穷小或有限大两种情形,而力矩可以有通过角动量的时间变化率计算或直接用距离叉乘受力计算两种方式,组合起来我们原则上可以有4种处理此问题的方式:①无穷小电流圈通过角动量的时间变化率计算;②无穷小电流圈通过距离叉乘受力计算;③有限大电流圈通过角动量的时间变化率计算;④有限大电流圈通过距离叉乘受力计算.我们主要采用方式①和④进行讨论;在④中把尺度取无穷小极限即回到②;③的计算过于复杂我们没有讨论.
以下我们先在本节讨论①,并由此给出一种对有力矩但不转动的可能解释.然后再在下节讨论④,并讨论其无穷小极限②,其中我们使用对电流圈中运动的小球计算出了电流圈的动量、角动量,给出了另一种对有力矩但不转动的可能解释.
对无穷小电流圈的情形,注意图1(c)和(d)正是我们在第1节中所讨论的一个点电荷与一个磁偶极子的体系.这里我们把磁铁看成是一个磁偶极子,我们先把磁铁缩成一个点,因而成为一个严格的点磁偶极子.点磁偶极子的问题搞清楚了,原则上把很多个点磁偶极子叠加起来就得到了有限尺寸的磁铁.若认为这种处理不够严格,在第3节我们直接对有限尺寸的磁铁进行计算.

图2 在S系和S′系中的小电流圈
前面提到的冲突是在取磁偶极子是电流圈的假设基础之上的,矛盾或冲突来自在运动的时候磁偶极子受电荷给予的力矩.为了讨论这个问题,我们先建立如图2的坐标系.S′系中点电荷和磁偶极子都静止,S′系相对于S系沿x轴正方向作速率为v的匀速直线运动.注意这个坐标系的xyz取向与Mansuripur原文中放入磁偶极子的坐标系取向有差别.如果我们把运动磁偶极子所受力矩的作用点选择在电荷所在点O′处,这时相当于是在S′系中对点电荷和磁偶极子组成的系统进行观察,因为点电荷和磁偶极子组成的系统相对于S′系静止,对应于图1(c),这个力矩可由电荷和磁偶极子的相互作用角动量M电流圈≡-d×P电流圈的时间变化率电流圈得到.而由式(10),对匀速运动,电流圈=0,而d又是个固定常数,因此电流圈=0,实际上并没有力矩,与观察结果一致.但是如果我们把力矩的作用点选择在O点处时,这时相当于是在S系中对点电荷和磁偶极子组成的系统进行观察,对应于图1(d),则M电流圈=l×P电流圈,求力矩电流圈=×P电流圈+l×电流圈.对于如图2所示的情况,式(10)的m× d与瓫的夹角θ刚好90°,cosθ刚好为零,所以运动电流圈的取值与静止电流圈的取值相同,都为P=.代入电流圈求出的力矩大小为τ=方向沿z轴负向.这个结果刘陆川和谢天佑也曾计算过.我们发现,的确出现了力矩.那么这个力矩会引起电流圈的转动吗?这实际上也是Science文章提出问题的出发点.通过观察发现,这个求出来的力矩与Mansuripur原文计算出来的力矩大小相同但方向相反.这里就把有力矩但不发生转动的第一种解释介绍给大家.参考文献[7]、[9]、[10]都提出了一个“hidden momentum”的说法.下面是参考文献[9]的一段原文:Different models that use current loops to represent a magnetic dipole predict that the dipole acquires a hidden momentum in the presence of the external electric field due to relativistic effects on the moving charges of the loops.This hidden momentum is counterbalanced by the electromagnetic momentum obtained from the integral in the whole space.按照这个说法,使用上述方法计算出来的动量是全空间的动量,而Mansuripur原文使用距离叉乘力的方法计算出来的力矩对应着一个所谓的“hidden momentum”,这两个动量大小相等,方向相反,刚好抵消.为了验证这个说法,我们使用文献[10]中“hidden momentum”的计算公式把在前面磁偶极子定义中讨论过的m和代入,可得刚好和全空间的动量大小相等,方向相反.由它代入角动量的变化率算出来的力矩就等于Mansuripur原文使用距离叉乘力的方法计算出来的力矩,磁偶极子所在位置处r=0,所以方向沿z轴正向.这个力矩和前面算出的全空间的力矩刚好抵消,无净力矩,因此电流圈不会产生转动.
下面来看看另一种将磁偶极子换成采用正负磁单极对的情况.按照式(8)P正负磁单极=0,选取O′点为力矩原点时,磁偶极子和点电荷的相互作用角动量M正负磁单极≡-d×P正负磁单极为零,磁单极所受的力矩M·正负磁单极自然为零.选取O点为力矩原点时,尽管l在不断变化,但是P正负磁单极=0,所以正负磁单极还是为零.在前面的内容中我们提到过电流圈有电流密度为-m×δ(r)纯的电流源而正负磁单极对没有电流源,这个差别也许就体现在有纯电流源的电流圈会产生所谓的“hidden momentum”,它的作用是抵消体系原来的电磁动量.
通过对这样两种不同的磁偶极子定义模型的计算,我们发现,不论是电流圈还是正负磁单极对,都得到不发生转动的情况.两种模型在理论上体现出的最大区别在于:电流圈构成的磁偶极子体系有相互作用角动量;而正负磁单极构成的磁偶极子体系根本没有相互作用角动量!这是我们在本文的一开始所特别强调的“磁单极有时也可以导致的极平庸的现象和结果”的明确显示.由此在这个体系里完全无法从磁偶极子是否转动上来区分磁偶极子是由电流圈构成的还是由正负磁单极构成的.实际上如果任何实验都测不出两种构成的磁偶极子的差别的话,也就意味着在现实世界电流圈足以替代正负磁偶极子对来顶替磁偶极子的角色.我们生活的世界也许真就不再需要磁单极的存在了.
到此为止,似乎讨论应该结束了.有些细心的读者会说:把磁偶极子压缩成一个点,再用点电荷到它的距离-d或者使用l叉乘它似乎不太合理.因为对有限大的电流圈,不同位置的电流应该用不同的距离矢量叉乘,这也许会造成新的差别,它是否会产生有效的力矩?也就是先算有限尺寸的磁单极所受的力矩,而不是先缩成点算力矩再叠加.这种对极限与求和的次序交换是否对本问题会造成差别呢?这个情形也就是我们的学生所具体研究和计算的问题,虽然结论相同,但具体计算相当复杂,我们把它们留在下节进行仔细讨论.
3 有限尺寸运动的磁偶极子受运动电荷的作用力矩
本节分为两个部分,一是运动的有限尺寸间隔的正反磁单极对受运动电荷的作用力矩,二是运动的有限大小的电流圈受运动电荷的作用力矩.我们发现,对于运动的有限尺寸间隔的正反磁单极对力矩严格为零.对于运动的有限大小的电流圈,的确存在力矩,但有另外一种不会发生转动的解释.
3.1 运动的有限尺寸间隔的正反磁单极对受运动电荷的作用力矩
相比于有限大小的电流圈,有限尺寸间隔的正反磁单极对的情况要简单得多(也就是本文的主题).我们首先建立如图3的坐标系,S′系中点电荷和磁偶极子都静止,S′系相对于S系沿x轴正方向作速率为v的匀速直线运动.根据Mansuripur的详细回复中的描述画出正负磁单极对,见图3.在由运动电荷q产生的电磁场中,磁单极受到洛伦兹力的作用为[13]

下面我们对正反磁单极对进行受力分析,在电荷q产生的磁场当中,正负磁单极都分别受到了沿y轴负方向的磁场力,见图4.在电荷q产生的电场当中,正负磁单极都分别受到了沿y轴正方向的电场力,见图5.由于运动电荷q产生的电场和磁场之间有下面的关系式而ε0μ0=因此我们可以得知,作用在正磁单极上的磁场力和电场力因为大小相等,方向相反,导致正磁单极受到的合力为零,对于负磁单极情况也是一样.因此,正负磁单极对不会受到力矩的作用,力矩为零.
3.2 运动的有限大小的电流圈受运动电荷的作用情况
这部分工作主要是班上的谢天佑同学做的,并在2015年5月13日的课堂上做了简化的介绍.根据计算,运动的有限大小的电流圈上下两边积累了不同电性的电荷,整个电流圈受到了比较复杂的电场力和磁场力的作用,但所受合力为零.虽然所受合力为零,但是电流圈的确受到了电磁力矩的作用,只是这个电磁力矩只引起了电流圈角动量的变化,而没有导致电流圈的转动.下面我们对这些结果进行一一详细说明.
图3 坐标系中的正负磁单极对
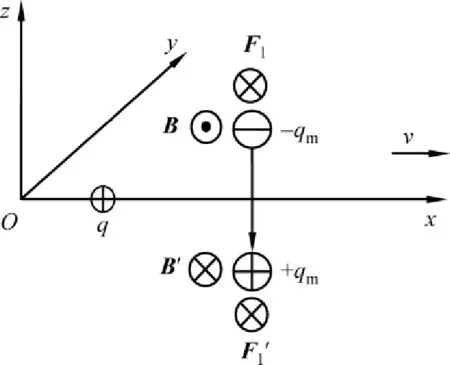
图4 磁单极对受磁场力的作用

图5 磁单极对受电场力的作用
3.2.1 运动的有限大小的电流圈受运动电荷的作用力
首先建立与上面磁单极取向一致的坐标系,此时,图1右下图中给出的运动电荷q和电流圈相对于S′系静止,设它们之间的距离为R′.在该系中观察到的电流圈是一个边长为l′的正方形,其上下左右四边的电流大小相等,都为I′,电流的绕行方向为逆时针方向,整个电流圈上下左右四边呈电中性状态,见图6.这里画出的电流圈实际上是有一定粗度的,存在截面积A′.在这里需要说明一下,为了在讨论的过程中不引起混淆,在S′系中观察的物理量我们都在字母的右上方加上一撇,在S系中观察的物理量的字母没有一撇.在S系中观察时(见图7),由于相对论效应,运动电荷q和电流圈之间的距离变短了,而且电流圈的上下边缩短了,左右边没有发生变化,形状变成了一个长方形,上下左右四边的电流大小发生了变化,同时电流圈的上下边积累了不同电性的电荷,计算如下:
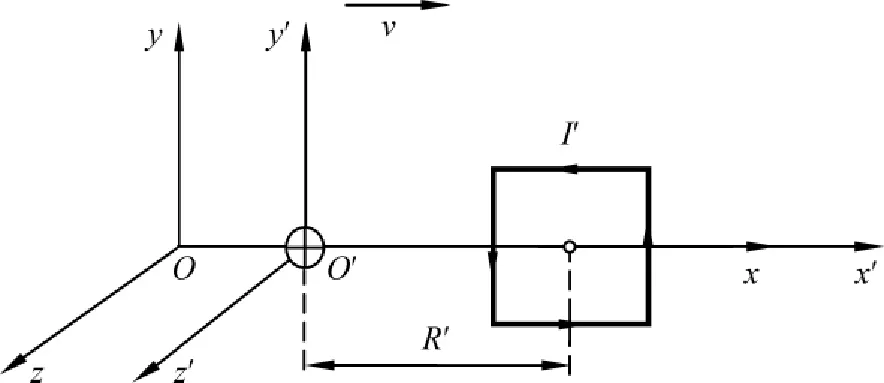
图6 建立的坐标系S和S′(电流圈在S′中静止)

图7 在S系中观察到的运动电荷和电流圈
根据费曼物理学讲义,在静止系S中观察到的运动直导线的电荷密度ρ和电流密度j与在一个以速率v相对静止系x轴正向运动的参考系S′(在该系中直导线静止)中观察到的直导线的电荷密度ρ′和电流密度j′之间的关系是

从S系观察到的电流圈上边导线横截面积不变,长度缩短,积累的电量为
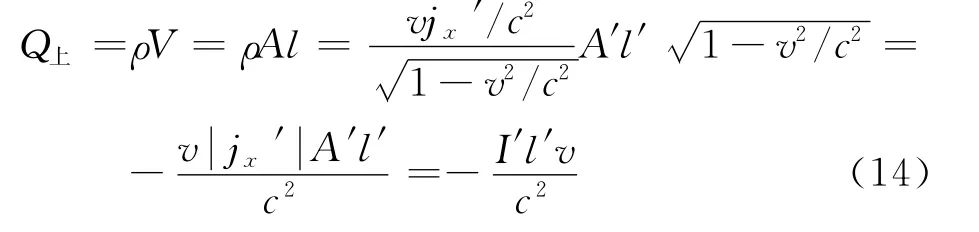
这里出现负号表明累计了负电荷,取负号的原因是电流圈上边导线的电流密度方向与导线运动方向相反.同样可以算出电流圈下边积累的正电量为电流圈左右两边没有电荷的积累.
根据I=jA及I′=j′A′及式(13)的后面3个式子,可以得到从S系观察到的电流圈上下边的电流为左右边的电流为
现在来考虑运动电荷q产生的电磁场对电流圈的作用.根据电动力学理论,在S系中,沿x轴方向运动的电荷q在空间产生的电场和磁场分别是

下面我们首先分析电流圈受到的电场力和磁场力作用,见图8.为使分析稍微简单一些,我们简化模型,假定只有一圈电流,并且放置在xy平面中,也就是说z=0.
从图8中可以看出,电流圈受到的力比较复杂.电流圈左右两边由于没有电荷的积累,所以不受到电场力的作用.上下两边受到电场力的作用.电流圈的上下左右因为都存在电流,均受到磁场力的作用.可以看出Fm左上=-Fm左下,Fm右上=-Fm右下,上下两边对应点受到的电场力在x轴上的分量也由于大小相等方向相反而抵消了,下面我们看看作用在上下两边的磁场力和在y轴方向的电场力能否相互抵消.只对电流圈下边的一点dx作分析.现在把导线看成一根线,它受到y方向上的电场力为

它受到y方向上的磁场力为
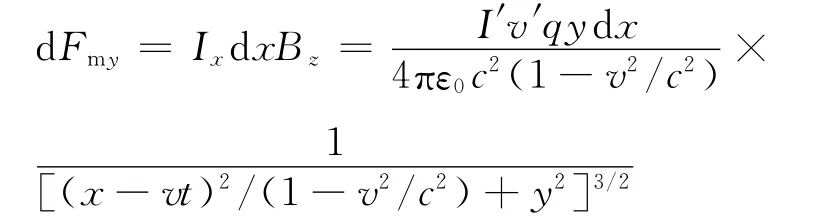
所以在电流圈的上下边这两个力也抵消了,因此我们可以得到结论:电流圈不受力的作用.

图8 电流圈受到的电场力磁场力和力矩分析
3.2.2 运动的有限大小的电流圈受运动电荷的作用力矩
整个电流圈不受力的作用,那么它也不受到力矩的作用吗?答案是否定的.在S系中,通过观察,我们发现如果以S系的原点O作为力矩中r的起点,则对力矩有贡献的电场力分别是Fex,F′ex,Fm左上,Fm左下,Fm右上,Fm右下,下面我们就分别计算这些有贡献的电场力和磁场力所产生的力矩.
我们的计算是在S系当中进行的.先看电场力的力矩.经过分析,电力矩τe沿z轴正向.电流圈上下两边对应位置的电荷受到的电场力在x轴上的分量大小相等方向相反,可以合在一起计算,并且可以看出在不同的受力点r与x轴之间的夹角θ不一样,但是rsinθ=y的值都是一样的为ly/2=l′/2.因此电场力力矩为


再来考虑磁场力的力矩.磁场力在电流圈左边和电流圈右边产生的力矩τm左和τm右分别沿z轴正向和z轴负向,总磁力矩为τm.与计算电场力力矩类似,发现左右受力点的r与x轴之间的夹角θ不一样,但两边rsinθ的值都为y,所以有

先计算对电流圈右边的作用

下面做一个积分变换技巧,先将(x-vt)2/(1-v2/c2)代换为x2′=R′+l′/2,上述积分变为
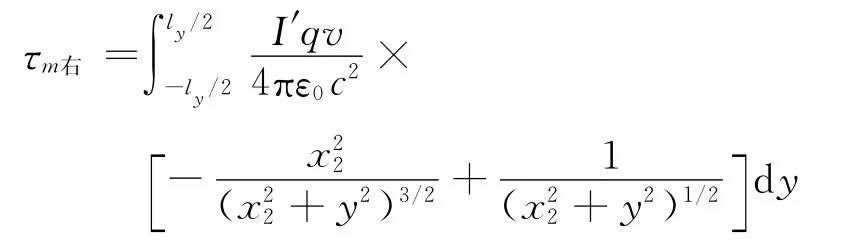

积分的上下限我们在后面再进行考虑.
积分第一项为

积分第二项为

注意到力矩τm左和τm右分别沿z轴正向和z轴负向,为了和沿z轴正向的电力矩τe叠加,取z轴正向为正,则τm右取负值,总的磁力矩为

综合电力矩和磁力矩,得到电流环受到的总力矩
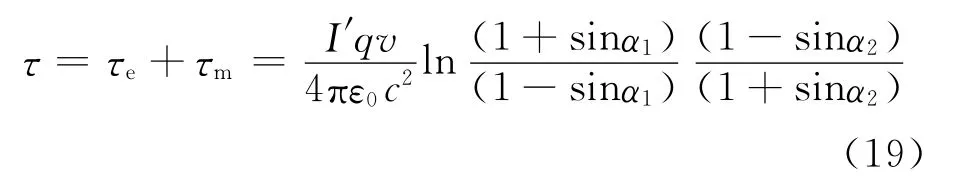
从上面的计算可以看出,电流圈的确受到一个不为零的力矩.
有限大尺寸的电流圈的力矩看起来比无穷小电流圈的力矩复杂的多,它们之间能够对应起来吗?下面来看看它们之间的对应关系.
在力矩原点选择O点处,无穷小电流圈力矩的大小在前面的计算中可以知道为其中m=I′S=I′l′2.代入上式有有限尺寸的电流圈力矩大小为上面式(19).其中无穷小力矩表达式中的d与第二式的R′相等,是同一个距离.
下面从
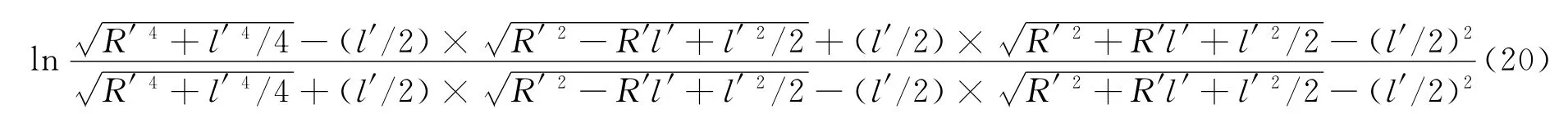
下面做一些技巧处理,把所有带根号项的根号去掉(可以这样做的原因是l′→0,是无穷小量),使用公式(1+x)n≈1+nx同理可得把去掉根号的量代入式(20),得到
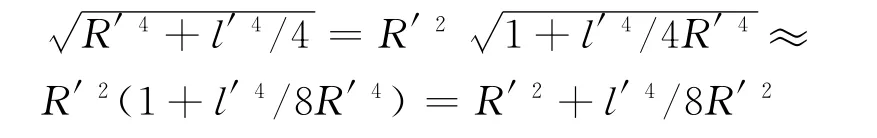
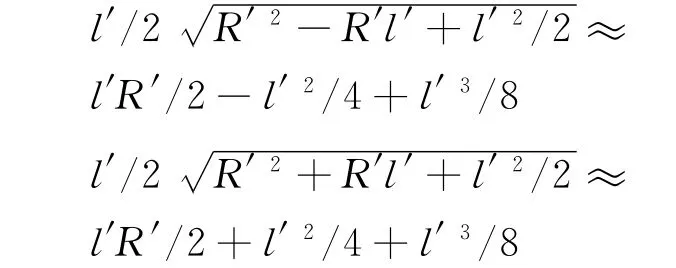


从上面的讨论可以看出,当l′→0时,有限大尺寸的电流圈和无穷小的电流圈的力矩统一起来了.那么这个力矩一定会引起电流圈的转动吗?这就是我们下面要讨论的问题.
3.2.3 运动的有限大小的电流圈受力矩作用但不转动
在前面无穷小电流圈的情况下我们已经对出现了力矩但电流圈不会发生转动的情况的一种解释进行了说明,即全空间的力矩和对应着“hidden momentum”的力矩相互抵消,无净力矩,不会发生转动.对于有限大电流圈情况,我们同样可以使用(其中电场的公式为上面的式(15),磁场除了式(16)还要考虑运动的电流圈产生的复杂磁场)计算出全空间的动量,从而进一步计算出相应的力矩,该力矩与3.2.2节计算出来的力矩抵消.但是由于上式计算过于复杂,我们就不详细进行讨论了.我们将在下面的内容中计算出与3.2.2节计算出来的力矩相对应的动量和角动量,并给出另外一种有力矩但不转动的解释.
对于有限大尺寸的电流圈,为了计算电流圈的电磁动量,建立如下微观模型.在把S系中整体呈电中性电流圈看作是一个带负电的管子和运动着的带正电e的小球组成,小球与管壁之间为弹性碰撞,无摩擦力,见图9.在稳态情况下,根据左右两边电流相等和整个回路的载流子能量相等可以导出
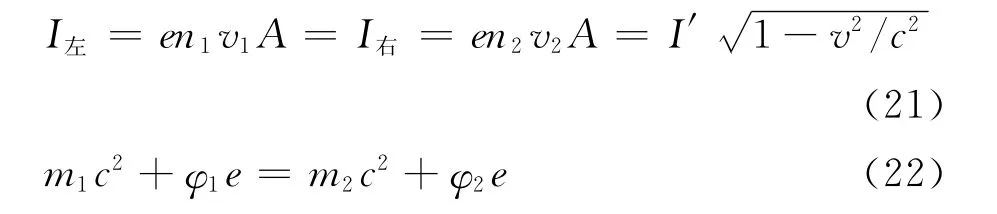
其中n1和n2为粒子数密度,v1和v2为小球的运动速率,m1和m2为小球的质量,φ1和φ2为运动粒子q产生的电势.

图9 电流圈内部的载流子
进一步写为


同样对上下边对应位置的灰色小球也做类似分析,可以得到这两个小灰球的质量m′1和m′2相等(因为φ′1和φ′2相等),还可得到

有了以上的准备工作,下面我们就可以计算电流圈的动量.整个电流圈的动量是每一个小球动量的叠加.对于x轴方向,动量为

对于y轴方向,动量为



可以看出,该电磁动量是一个不随时间变化的量,而且它的方向保持为y轴正向.上面的讨论虽然是在S系当中得到的结果,但是对于S′系,结果是一样的,只是具体计算时因为有些物理量在S系和S′系中不一样,要把相应物理量的取值改变.
相应地,我们可以使用L=r×p,直接通过对每个运动小球的积分计算出整个电流圈角动量的值.其中对于每一个小球角动量的大小L=rpsinθ中的r和sinθ虽然都是变量,但rsinθ为一恒定值x.求出的角动量为

方向沿z轴正向.
角动量的变化率
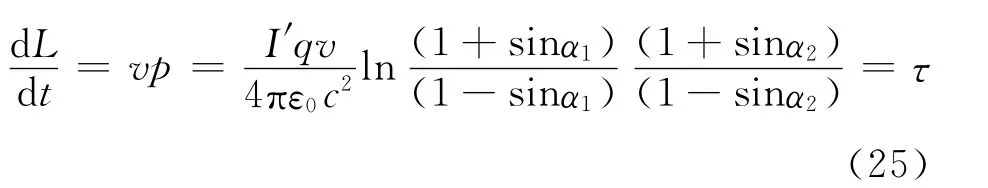
通过对电流圈中运动着的小球积分,我们得到了一个与力矩有对应关系的角动量.我们发现该角动量的变化率刚好等于电流圈所受到的力矩.到此人们可能还会问,虽然这个力矩对应上了一个角动量的变化率,但是怎么知道它不会引起磁铁的转动呢?就此我们引入第二种解释.算出的P沿y轴正向,可以写成球坐标系下的形式
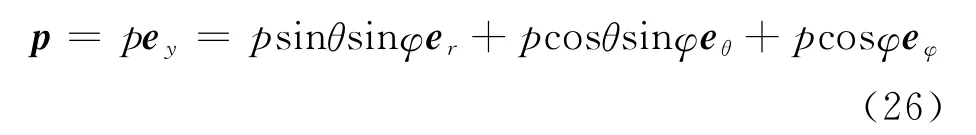
电流圈的情况比较复杂,在此做一下小结.我们对无穷小电流圈计算出了运动的电荷和磁偶极子体系的动量和相应力矩,“hidden momentum”和相应力矩,并给出了电流圈不发生转动的第一种解释:两个力矩相互抵消,无净力矩,不发生转动.对有限大的电流圈使用距离叉乘力的方法计算出了电流圈受到的力矩,使用对电流圈中运动的小球计算出了电流圈的动量、角动量,角动量的变化率正好对应于力矩.并从动量不发生变化,电流圈没有角度的变化给出了电流圈不发生转动的第二种解释.
4 结语
电流圈构造的磁偶极子与正反磁偶极子对构造的磁偶极子所产生的电磁场在外部完全相同,在内部相互反号,大小相差两倍.在磁偶极子和点电荷形成的系统中无论是在静止系还是在运动系,磁偶极子不管是两种构造中的哪种都不会发生转动.只是磁偶极子若是由正反磁单极对构造的,体系的相互作用能动量和角动量都为零,因而十分简单和平庸;而若磁偶极子若是由小电流圈构造的,体系的相互作用能动量和角动量除了静止系的能量为零之外一般都不为零.
参考文献
[1] 王青.电磁学与电动力学中的磁单极——Ⅰ[J].物理与工程,2013,23(6):8-11.
[2] 王青.电磁学与电动力学中的磁单极——Ⅱ[J].物理与工程,2014,24(5):29-33.
[3] 王青.电磁学与电动力学中的磁单极——Ⅲ[J].物理与工程,2015,25(4):19-24.
[4] 王青.电磁学与电动力学中的磁单极——Ⅳ[J].物理与工程,2015,25(5):33-40.
[5] Mansuripur M.Trouble with the Lorentz law of force:Incompatibility with special relativity and momentum conservation[J].Phys Rev Lett,2012,108:193901.
[6] Cho Adrian.Textbook electrodynamics may contradict relativity[J].Science 2012,336:404.
[7] Vanzella D A T.Comment on“Trouble with the Lorentz law of force:Incompatibility with special relativity and momentum conservation”[J].Phys.Rev.Lett.2013,110:089401.
[8] Barnett S M.Comment on“trouble with the lorentz law of force:Incompatibility with special relativity and momentum conservation”[J].Phys.Rev.Lett.2013,110:089402.
[9] Saldanha P L.Comment on“trouble with the lorentz law of force:Incompatibility with special relativity and momentum conservation”[J].Phys.Rev.Lett.2013,110:089403.
[10] Khorrami M.Comment on“trouble with the lorentz law of force:Incompatibility with special relativity and momentum conservation”[J].Phys.Rev.Lett.2013,110:089404.
[11] Mansuripur M.Mansuripur replies:[J].Phys.Rev.Lett.2013,110:089405.
[12] Mansuripur M.Mansuripur replies:[J].Proc.of SPIE.2012,8455:845512.
[13] 范秀华,张祥雪,程艳霞,等.磁单极与磁洛伦兹力[J].大学物理,2007,26(1):22-25,43.
MAGNETIC MONOPOLE IN ELECTROMAGNETISM AND ELECTRODYNAMICS—Ⅴ
Chen Li1Wang Qing2
(1College of Engineering,Dali University,Yunnan Dali 671003;2Department of Physics,Tsinghua University,Beijing 100084)
AbstractAs the last one of a series of five individual papers and in contrast to previous papers,we introduce a special non-peculiar property of magnetic monopole as popular science in the frameworks of electromagnetism and electrodynamics.In this paper,we mainly focus on the differences of magnetic dipoles defined by small current loop and that by the positive and negative monopole pair.We will analysis the possible phenomena for the system consisted from a point charge and a magnetic dipole,and show that the magnetic dipole constructed by the positive and negative monopole pair is much simple and trivial than that by current loop.
Key wordsmagnetic dipole;current loop;positive and negative monopole pair
作者简介:陈丽,女,副教授,主要从事物理教学和相关研究工作;王青,男,教授,主要从事理论物理的科研和教学工作,研究方向为量子场论与基本粒子理论.wangq@mail.tsinghua.edu.cn
收稿日期:2015-07-06

