电偶极子和磁偶极子场分布相似性的一种解释
焦重庆
(华北电力大学 电气与电子工程学院, 北京 102206)
电偶极子和磁偶极子场分布相似性的一种解释
焦重庆
(华北电力大学 电气与电子工程学院, 北京 102206)
电偶极子电场与磁偶极子磁场具有相似的空间分布。然而,这种相似性并非显而易见:电偶极子由一对等量异号电荷组成,而磁偶极子则是一个电流回路。本文从矢量场边值问题的唯一性定理出发,得出了面散度源和面旋度源产生的矢量场分布的一种等价关系,进而对电偶极子电场与磁偶极子磁场空间分布的相似性进行了解释。
电偶极子;磁偶极子;唯一性定理;边值问题
0 引言
电偶极子和磁偶极子属于电磁场理论中的基本模型[1-3]。在“电磁场”课程的静电场部分,电偶极子指的是由两个相互临近的等量异号电荷组成的电荷系统。提出电偶极子这一基本模型的作用是为讲解介质的极化电场作铺垫。此外,在“电磁场”课程的电磁辐射部分,电偶极子(此时电荷量为时变的)还可以指电偶极子天线。在“电磁场”课程的恒定磁场部分,磁偶极子指的是一个闭合的电流回路。此时,提出磁偶极子这一基本模型是为讲解媒质磁化后的磁场作铺垫。此外,在“电磁场”课程的电磁辐射部分,磁偶极子(此时电流为时变的)还可以指磁偶极子天线。
有趣的是,为何把一个电流回路叫做磁偶极子?可能的原因有二:①由于至今仍未发现带有磁荷的粒子(磁单极子),故无法采用与构建电偶极子类似的方法来构建磁偶极子,即无法用一对等量异号的磁荷来表示磁偶极子;②用电流回路表示的磁偶极子产生的磁场在空间的分布与电偶极子产生的电场的空间分布是相同的。也就是说,用电流回路表示的磁偶极子与用等量异号的磁荷构成的“理想磁偶极子”在产生磁场的效果上是等价的。从这个意义上说,电流回路可以替代等量异号磁荷,因而被等效成磁偶极子。
然而,带来的问题是,为什么电流回路构成的磁偶极子产生的磁场与电偶极子电场的空间分布是一致的?虽然课本上给出的就是如此结果,但毕竟不便于理解。考虑到,“理想磁偶极子”(本文指一对临近的等量异号磁荷)产生的磁场与电偶极子产生的电场有相同的空间分布是显而易见的。因此,该问题可以换一个角度理解,即为什么电流回路构成的磁偶极子产生的磁场与由等量异号磁荷构成的磁偶极子产生的磁场具有相同的分布。本文从唯一性定理出发,对该问题给出了解释。
1 电偶极子场与磁偶极子场的相似性
“电磁场”课本中介绍的电偶极子和磁偶极子的模型如图1所示。

(a) 电偶极子 (b)磁偶极子
图1(a)中,q为电荷量,d为电荷间距。以两电荷的中心为坐标原点,由负电荷指向正电荷的方向为z轴方向,则自由空间中电偶极子电场的空间分布可以表示成:
(1)
式中,p=qd为电偶极子的电偶极矩。
图1(b)中,I为电流,S为电流回路包围的面积。以S的中心为坐标原点,以与回路所在面垂直且与电流环形方向成右手螺旋关系的轴线为z轴,则自由空间中磁偶极子磁场的空间分布可表示成:
(2)
式中,m=IS为磁偶极子的磁偶极矩。
比较式(1)和(2),不难看出,两种场的空间分布一致。需要强调的是,上述等价关系成立的前提是场点位于偶极子的远场区。在近场区,两者显然不同,前者是有散无旋场,后者是无散有旋场。然而,如果电偶极子的电荷间距尽可能小,同时磁偶极子的回路半径也尽可能小,则两者的场分布能够在靠近偶极子的区域内也能保持一致。
2 面散度源和面旋度源的等效关系
如图2所示,某矢量场F在体积V内均匀分布,即各点的场强大小相同、方向也一致。假设在区域V外F为零。从矢量场唯一性定理(如亥姆霍兹定理)考虑,矢量场由散度、旋度和边界条件唯一确定[4]。对于图2所示的问题,S被看成是分界面而不是边界,场域为整个空间,则从矢量场的分界面条件出发,为了达到这种特殊的场分布,必然要求S上有以下两种面源存在(这种思路类似于电磁场理论中的等效原理[5]):
1)面散度源
ρs=en·(F2-F1)=-en·F
(3)
2)面旋度源
Js=en×(F2-F1)=-en×F
(4)
式中,en为S的法向单位矢量,从S内部指向外部。F1指F在S内侧的值,F2指F在S外侧的值。

图2 局限在任一体积内的常矢量场
由于F在空间其它区域均无散且无旋。故F的场源只包括上述面散度源和面旋度源。即在上述面散度源和面旋度源的共同作用下,可以产生上述被局限在S内部的常矢量场:此时,上述两种面源产生的场在V内部叠加的效果是形成常矢量场,在V以外区域则相互抵消。类比自由空间面电荷分布产生的电位移矢量D,可以得出面散度源对矢量场F的贡献为
(5)
类比自由空间面电流分布产生的磁场强度H,可以得出面旋度源对矢量场F的贡献为
(6)
对于位于V外部的场点P,式(5)和(6)叠加等于零。实际上,我们也可以通过直接的数学推导来证明这一点。
如果把F看成电位移矢量D,则面散度源对应面电荷,而面旋度源对应面磁流(磁荷运动形成磁流)。如果把F看成磁场强度H,则面散度源对应面磁荷,而面旋度源对应面电流。
3 相似性的解释
如图3所示,假设自由空间中沿z轴方向的均匀磁场H仅仅分布在高度h、半径a的圆柱体内。则要求在圆柱体的上端面S1存在如下密度的面磁荷分布(定义磁感应强度B的散度为磁荷体密度):
ρms1=μ0H
(7)
在圆柱体的下端面S2存在如下密度的面磁荷分布:
ρms2=-μ0H
(8)
在圆柱体的侧面S3存在如下密度的面电流分布:
JS=H
(9)
该电流沿与z轴呈左手螺旋关系的方向流动。
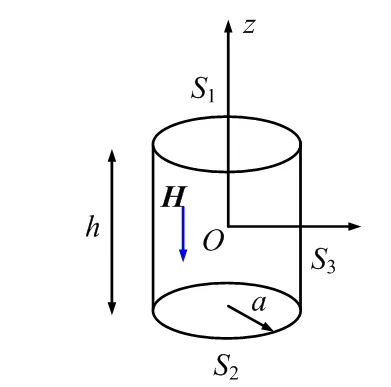
图3 局限在一圆柱体内的均匀磁场
假设圆柱体的半径趋向于零,则面磁荷分布被压缩成一个点磁荷,其磁荷大小为
qm=πa2ρms1=πa2μ0H
(10)
上端面的磁荷与下端面的磁荷构成具有如下偶极矩的“理想磁偶极子”:
m′=qmh=πa2μ0Hh
(11)
依据电荷和磁荷的对称关系,磁荷磁场与电荷电场的对应关系:
E↔H,D↔B,ε0↔μ0,qe↔qm,p↔m′
(12)
式中qe代表电荷,qm代表磁荷。从式(1)、(11)和(12)可以得出式(11)表示的磁偶极子产生的磁场强度H为
(13)
现在假设圆柱体的高度趋向于零,则面电流分布被压缩成一根圆形的线电流,其电流大小为
I=Jsh=Hh
(14)
它相当于如下偶极矩的磁偶极子:
m=πa2I=πa2Hh
(15)
可以看出,式(11)给出的基于电流定义的磁偶极矩与式(15)给出的基于磁荷定义的磁偶极矩之间相差一个常数μ0,但这并不影响最终的结论。
依据第2节的分析,如果将电流的方向反过来,即该电流沿与z轴呈右手螺旋关系的方向流动。然后,该电流产生的磁场将完全等同于上述“”理想磁偶极子“”产生的磁场。此时,式(15)表示的基于电流定义的磁偶极子产生的磁场强度H的表达式就是式(13)。在式(13)中,将式(15)代入,有
(16)
相应的,磁感应强度B为
(17)
可以看出,式(17)与式(2)完全相同。需要指出的是,上述等价关系只在圆柱体外部区域成立,这一点与第1节末尾所述的电偶极子场与磁偶极子场只在远场区相同的规律类似。
4 结语
本文基于矢量场的唯一性定理和分界面条件证明了对于一个闭合曲面,通过在曲面上放置适当的面散度源和面旋度源,可在曲面内产生均匀矢量场,在曲面外产生零矢量场。反之,面散度源和面旋度源可以在曲面外产生相同的场。由此,面电荷分布可以与面磁流分布产生相同的电场,而面磁荷分布可以与面电流分布产生相同的磁场。
基于上述理由,可以证明基于电流回路定义的磁偶极子产生的磁场等同于理想磁偶极子(等量异号磁荷)产生的磁场。而又因电偶极子的电场与“理想磁偶极子”产生的磁场具有相同的空间分布。最终对磁偶极子磁场分布与电偶极子电场分布的相似性给出了解释。
[1] 倪光正. 工程电磁场原理[M]. 北京: 高等教育出版社, 2009.
[2] 冯慈璋,马西奎. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000.
(焦重庆文)
[3] 王泽忠,全玉生,卢斌先. 工程电磁场[M]. 北京: 清华大学出版社, 2011.
[4] 雷银照. 电磁场[M]. 北京: 高等教育出版社, 2008.
[5] 夏明耀、王均宏. 电磁场理论与计算方法要论[M]. 北京: 北京大学出版社, 2013.
A Simple Explanation for the Similarity of Field Distributions of Electric Dipole and Magnetic Dipole
JIAO Chong-qing
(SchoolofElectricalandElectronicEngineering,NorthChinaElectricPowerUniversity,Beijing102206,China)
The electric field distribution of an electric dipole is similar with the magnetic field distribution of a magnetic dipole. However, this similarity is not obvious and is difficult to be understood due to the fact that: an electric dipole consists of a pair of separate electric charges with equal magnitude and opposite sign, but the magnetic dipole is a closed circulation of electric current. A kind of equivalent relationship between the vector field from a surface divergence source and that from a surface rotation source is obtained by using the uniqueness theorem of the boundary problem of a vector field. Based on this relationship, the similarity can be explained easily.
electric dipole; magnetic dipole; uniqueness theorem; boundary problem
2015-04-12;
2016-05-02
焦重庆(1981-):男,博士,副教授,主要从事电磁场理论和电磁兼容技术方向的教学和科研工作,E-mail: cqjiao@ncepu.edu.cn
G642.0
A
1008-0686(2016)03-0031-04

