返包式土工格栅加筋土挡墙动态行为研究

王 贺，杨广庆，刘华北，刘伟超，吴连海

(1.北京交通大学 土木建筑工程学院，北京 100044；2.石家庄铁道大学 土木工程学院，河北 石家庄 050043；3.华中科技大学 土木工程与力学学院，湖北 武汉 430074；4.铁道第三勘察设计院集团有限公司，天津 300142)

对于大型结构及地基而言，由于试验设备、场地大小及资金等的限制，只能以缩尺模型进行试验。高速铁路加筋土挡墙进行模型试验的重要目标之一，是将原型挡墙在外荷载作用下的力学现象在挡墙模型上进行相似模拟，以测量模型结构中的土压力、位移、加速度等相关物理量，总结挡墙的变形行为，再借助一定的相似关系推算到原型中，确保原型墙的稳定。

关于加筋土挡墙的动力学行为，GÖBLE等[1]利用室内模型箱研究加筋土挡墙在列车荷载作用下拉筋的合理位置及承载力和沉降的变化情况。MAHER等[2]利用共振柱试验对加筋砂土的动力反应情况进行测试。文献[3，4]通过多锚式加筋土挡墙的足尺振动台试验得到挡墙共振频率随墙高增加而减小的结论。LIU等[5]采用有限元方法得到地震荷载作用下多级加筋土挡墙与单级墙在共振频率、墙面位移等方面的不同。杨果林等[6-9]通过动力荷载作用下的模型试验模拟不同形式铁路加筋土挡墙路基结构，得到其动态响应特性。李昀[10]通过模型试验对格宾加筋土挡墙在车辆和地震荷载作用下的动力学响应和抗震性能进行系统研究，得到这种新型加筋土挡墙的动态响应规律。蒋建清等[11]通过引入筋-土、面板-土、面板-面板接触单元，建立加筋土挡墙的有限元模型，采用ANSYS模拟加筋土挡墙，得出关于加筋土挡墙动力响应的定性结论。李海深等[12]运用有限元计算方法建立加筋土弹塑性本构模型，编制加筋土挡墙在动荷载作用下的通用数值计算程序。

虽然目前国内外学者对于加筋土挡墙进行了一系列试验研究，但系统研究加筋土挡墙在高速行车荷载下动态响应规律的较少。本文通过返包式加筋土挡墙室内模型动力加载试验，系统分析加筋土挡墙的动态响应特性及其形成原因。

1 试验方案

挡土墙模型面板结构为土工格栅加筋返包式。为使模型试验结果真实反映列车荷载作用下土工格栅加筋土挡墙原型的变形行为，根据试验装置的尺寸，通过对不同模型的比例尺方案进行讨论分析，应用方程分析法与量纲分析法推导土工格栅加筋土挡墙模型试验需符合的相似关系，确定模型的几何相似比Cl=4，填料容重相似比Cγ=1，黏聚力相似比Cc=1，摩擦角相似比Cφ=1，土工格栅拉伸模量相似比CE=2。

1.1填料

填料为碎石土，颗粒分析曲线如图1所示。

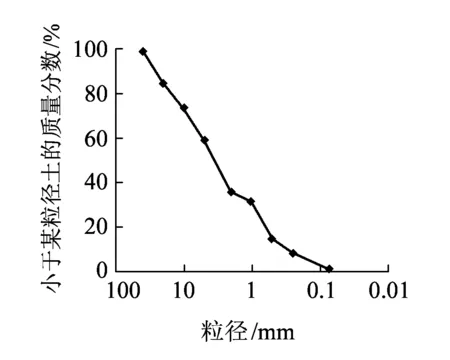
图1 碎石土颗粒分析曲线

经计算，该填料的不均匀系数Cu=17.48，曲率系数Cc=0.54，属级配不良填料。

1.2 土工格栅特性

加筋材料选用单向拉伸HDPE塑料土工格栅，其尺寸及力学特性见表1。

表1 土工格栅几何尺寸及力学特性

1.3 模型箱、挡墙尺寸及仪器布置

模型箱(图2)长3.5 m、宽1.0 m、高2.0 m。设计挡土墙模型长3 m、宽1.0 m、高1.65 m；土工格栅竖向间距30 cm，铺设长度2 m，返包部分长0.5 m；承载部件为工字钢。监测传感器包括动土压力盒、静土压力盒、柔性位移计、加速度计、百分表等(图3)。

图2 模型试验

1.4 填筑要求及加载方案

挡墙填料采用小型手扶式冲击夯压实。经击实试验和试压测得填筑控制指标见表2。

图3 加筋土挡墙尺寸及监测仪器布置(单位：cm)

注：(1)各层水平放置的土压力盒与柔性位移计位于同一层上，为显示清楚，在本图中竖向错开了一定距离；(2)最上层动土压力盒应位于静土压力盒所在位置，横向错开一定距离，为显示出来则如图中所画；(3)仪器编号中，J为加速度计，B为百分表，R为柔性位移计，HT(VT)为水平(竖直)放置的动土压力盒，HJ(VJ)为水平(竖直)放置的静土压力盒。

表2 填料填筑控制指标

根据TB 10621—2009《高速铁路设计规范》中关于高速铁路路基面动应力幅值计算方法及国内外高铁线路实测值(表3)，确定动态加载幅值为40～80 kPa、60～100 kPa、80～120 kPa三种；加载频率为4 Hz、6 Hz、8 Hz、10 Hz四种。以三种加载幅值和四种加载频率进行正交试验，每种条件加载10万次，共加载120万次。加载过程中采用动态采集仪对数据进行采集，其中每加载1万次暂停15 min，对静土压力盒、百分表及柔性位移计数据进行采集。

表3 路基表面实测动应力[13]

2 主要试验研究内容

本试验通过修筑大尺寸模型，利用加载系统对其施加动荷载来模拟加筋土挡墙墙顶承受动荷载的情况，分析挡墙内土体和筋材的应力应变分布规律及形成原因。测试及分析的主要内容如下：

(1)测试挡墙加速度，分析变化规律及形成原因；

(2)测试挡墙墙面水平位移和竖向沉降，观察其分布规律并分析原因；

(3)测试并分析挡墙内竖向和水平动土压力的分布规律及形成原因；

(4)测试动载施加后挡墙内水平和竖向残余土压力，分析其变化规律及形成原因；

(5)测试筋材应变，分析其变化规律及形成原因。

3 试验结果与分析

3.1 竖向加速度分布规律

考虑到挡墙上部受振动荷载影响较大，对加速度较敏感，因此在上部埋设3个加速度传感器。挡墙上部不同位置的加速度峰值均值随加载频率、次数及加载量变化的曲线如图4所示。由图4可见：

(1)在加载量不变的情况下，振动加速度随加载频率的增加而增大。由于频率变换有一定的突变性，因此加速度呈台阶式增长。频率在4 Hz、6 Hz和 8 Hz之间变换时，加速度的增长幅度较小且较平均，频率增加到10 Hz后加速度有较大幅度增长。

(2)频率相同的情况下，振动加速度随外荷载和加载次数的增加略有增长，变化不大；加载量和频率均不变时，随加载次数的增加，加速度几乎不变。这是由于土工格栅的变形很小，在其水平限制作用下，墙内土体在夯实和荷载作用下很快形成结构稳定的整体，同样只具有较小的变形。因此，在疲劳荷载作用下，不发生共振时，挡墙内振动加速度的变化较小。

(3)荷载为80～120 kPa时，加速度增幅变小，相同频率下，相比前两级荷载增加也较小。这是由于加筋复合体密实度进一步增大、刚度变大的缘故。从理论上分析，一个构件刚度一定时，激振力越大，响应越大；激振力一定时，刚度越大，响应越小。试验结果与该理论相符。

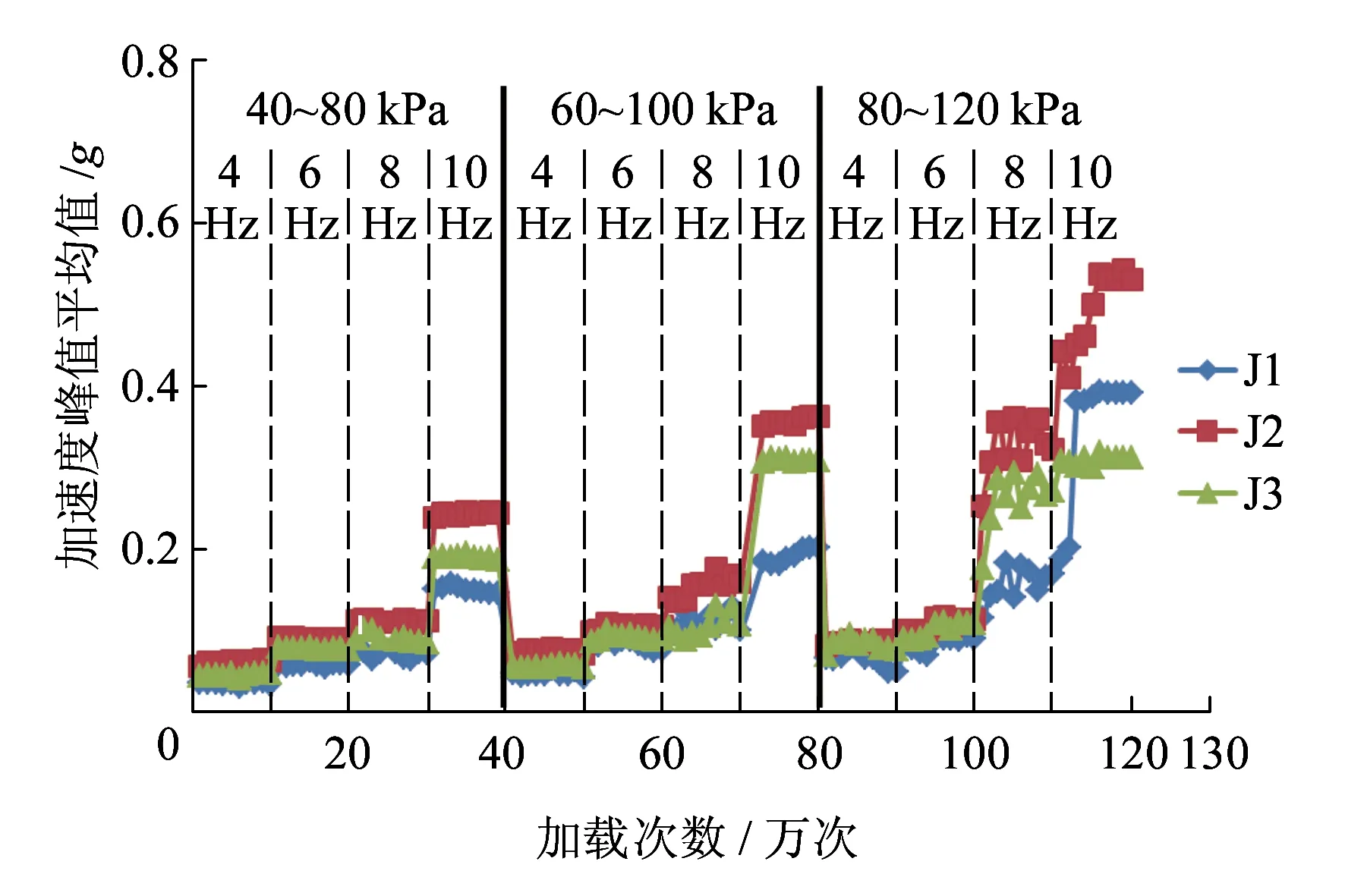
图4 挡墙加速度变化规律

综合以上分析，加筋土挡墙内加速度受加载频率的影响较大，受加载次数和荷载大小的影响较小。应用到实际工程，即加筋土挡墙受列车速度的影响较大，受列车轴重和运行次数的影响较小。轴重越大，加速度受速度的影响越小。

3.2 墙面变形特性分析

3.2.1 墙面累积水平位移分析

墙面累积水平位移随加载次数的分布如图5所示。

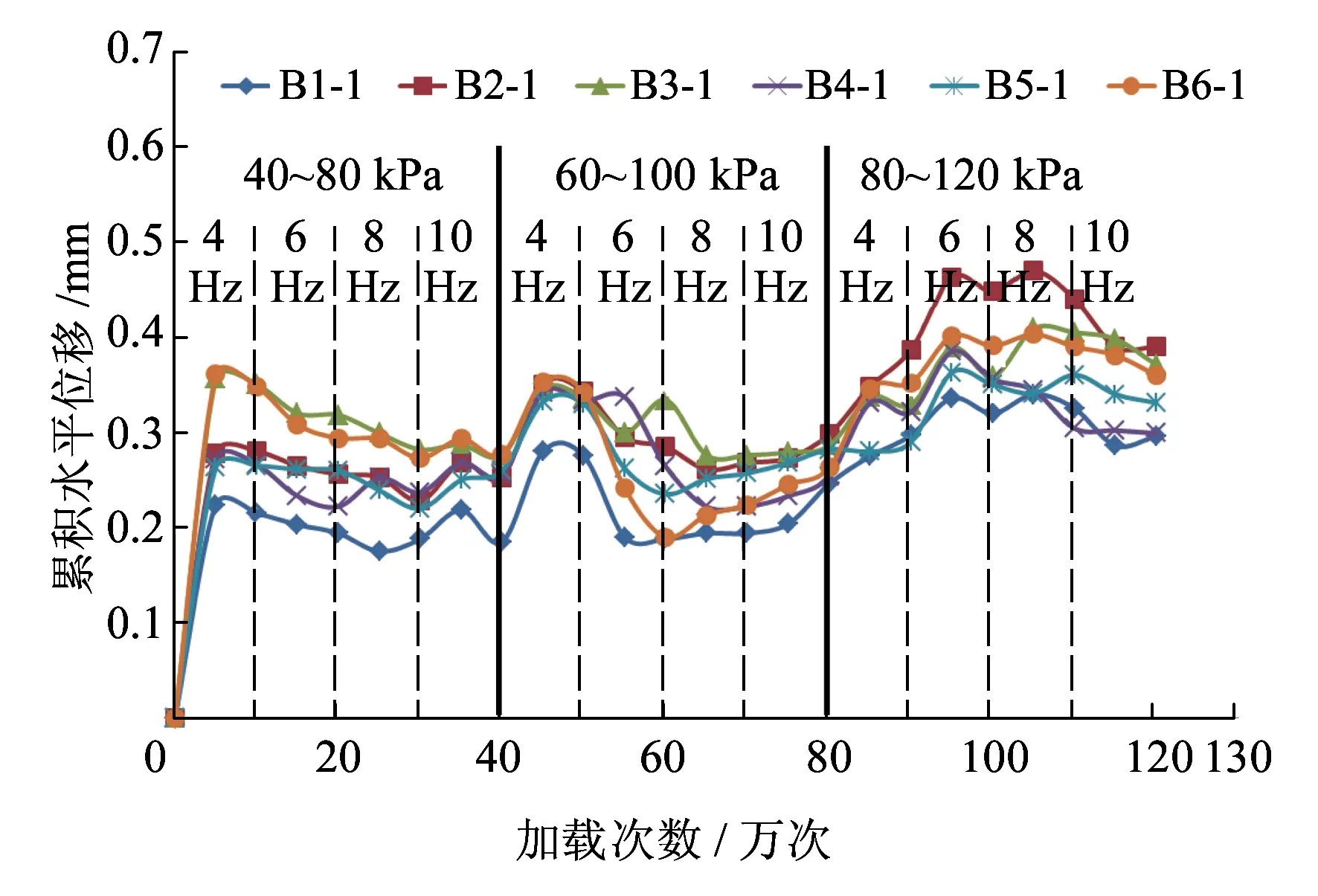
图5 墙面累积水平位移随加载次数的分布

(1)前两级加载时墙面累积水平位移只在开始加载时迅速增加，随后趋于稳定，施加第三级荷载后才出现较明显的增长态势。可见前两级荷载不足以使土工格栅产生较大应变，从而限制了墙面位移。说明土工格栅的拉伸变形对荷载增加的敏感性较差。

(2)每级加载开始时有突增趋势，然后逐渐减小并趋于稳定。这主要是因为荷载突然变换，增加的冲击力瞬时施加到原本稳定的结构，使靠近墙面处的土颗粒重新排列，墙面位移突然增大。随着加载次数的增加，重新形成更加密实、稳定的结构，墙面水平位移有少量恢复。

(3)墙面水平位移的变化受荷载的影响较大，受频率和荷载重复次数的影响较小。

图6为不同荷载和频率作用下墙面累积水平位移沿墙高的分布。由图6可见墙面累积水平位移沿墙高基本呈S形曲线分布。随着荷载应力水平的增大，最大水平位移出现位置逐渐从挡墙的中部(90 cm高)移到中下部(60 cm高)。这主要是因为外加动载作用对挡墙的影响范围从高到低逐渐扩大，随着动荷载的增大，影响深度增大。墙面最大水平位移为0.448 mm，约为墙高的0.027%。

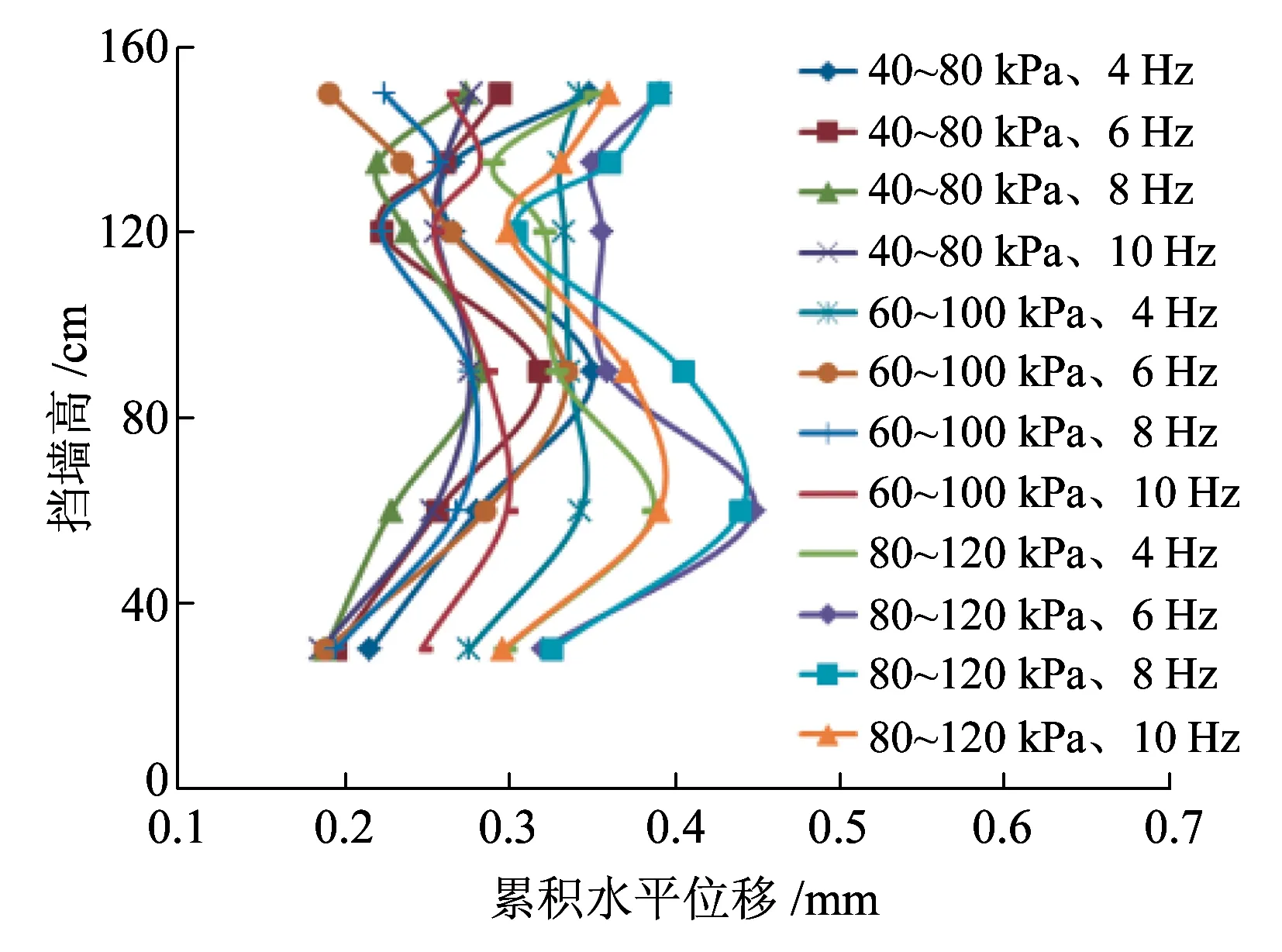
图6 墙面累积水平位移沿墙高的分布

3.2.2 墙面累积竖向沉降分析

墙面累积竖向沉降随加载次数以及沿墙高的变化曲线如图7、图8所示。

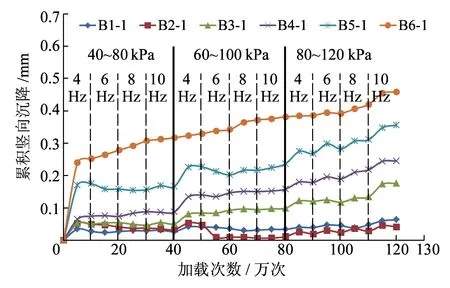
图7 墙面累积竖向沉降随加载次数的分布

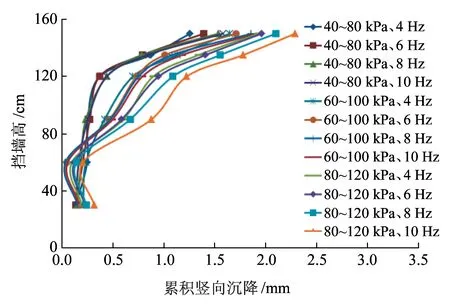
图8 墙面累积竖向沉降沿墙高的分布

墙面累积竖向沉降随加载次数的增加呈线性增长趋势，基本不受荷载和频率变换的影响，其沿墙从高到低逐渐减小，速率逐渐降低。墙面最大竖向沉降出现在顶部，为2.29 mm，约为墙高的0.14%。

3.3 动土压力分布规律

3.3.1 竖向动土压力分布规律

图9为不同高度层位处竖向动土压力峰值平均值随加载频率、次数及加载量的变化情况。

从图9可以看出：

(1)沿筋材方向，竖向动土压力最大值出现在加载点附近，分别向墙面和筋材末端方向逐渐减小，层高越高减小速率越大。同时在筋材末端竖向动土压力沿墙高从高到低逐渐增加，增长趋势逐渐变缓。这是由于动土压力的影响范围从高到低逐渐扩大。

(a)h=0.45 m

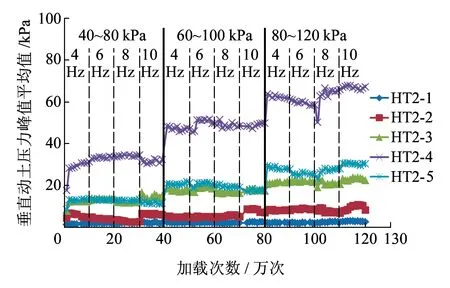
(b)h=1.05 m

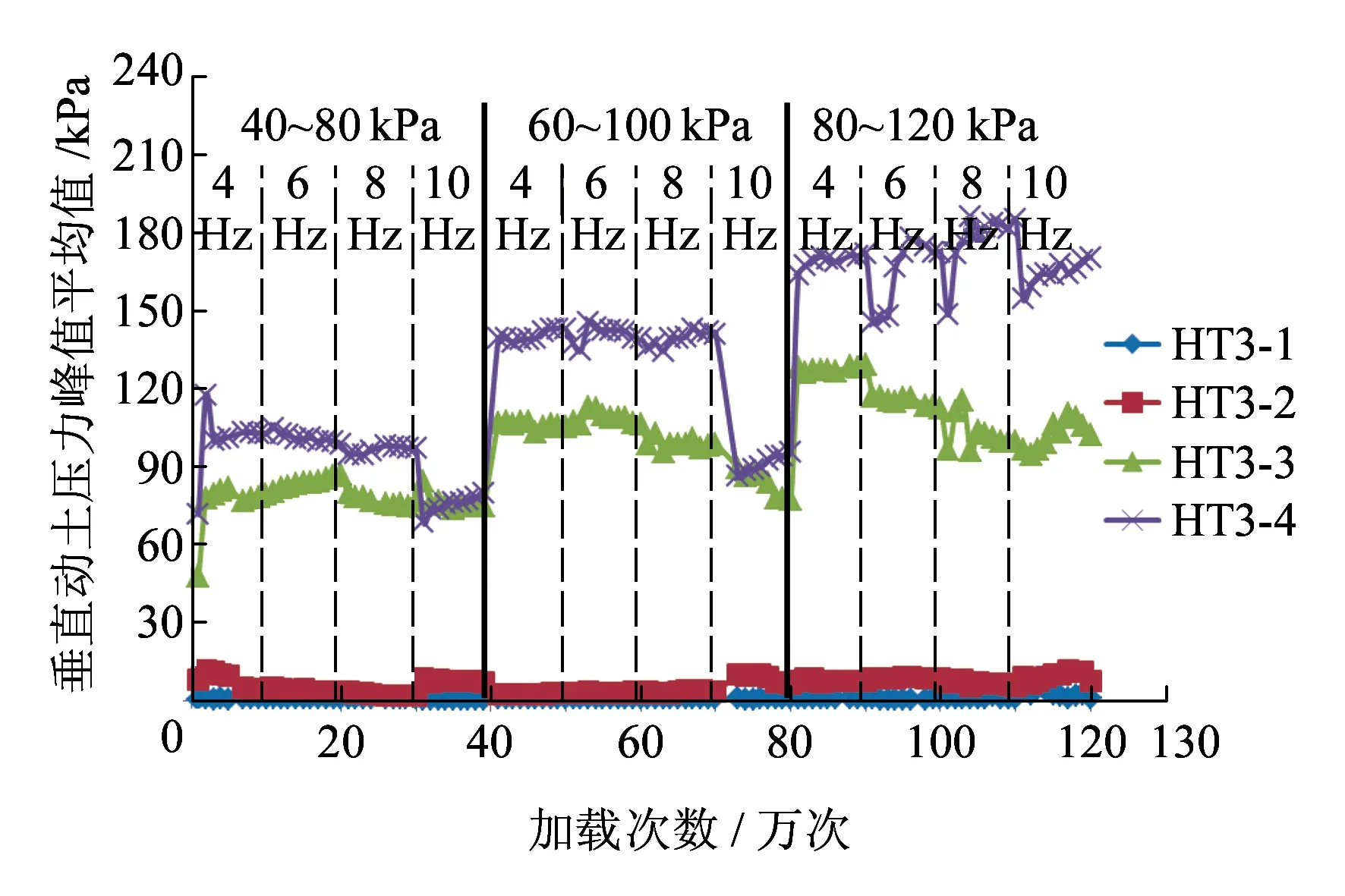
(c)h=1.35 m图9 竖向动土压力分布规律

(2)竖向动土压力受加载次数和荷载大小的影响较大，受加载频率影响较小。荷载不变时，动土压力随加载频率的增加略有增大然后趋于稳定。荷载和频率均不变时，竖向动土压力在刚施加本级荷载时略有增加，加载频率大于4 Hz后几乎不再变化，甚至有所减小。相同频率不同荷载的情况下，竖向动土压力随着荷载增加而增大，且增大速率逐渐减小。上述情况的出现主要是挡墙内加筋复合体在动应力和筋材共同作用下越来越密实，刚度变大结构性增强的原因。

(3)靠近墙面处各层动土压力在荷载不变的情况下随频率的增加稍有减小，这主要是由于墙面出现向外的水平位移释放了部分应力。

图10为挡墙内靠近墙面处土体在不同荷载和加载频率作用下竖向动土压力峰值平均值沿挡墙高度的变化曲线。从图10可以看出：沿墙从高到低，竖向动土压力呈衰减趋势，衰减速率逐渐降低。沿墙高从1.35 m 降低到0.9 m，竖向动土压力衰减约83%。

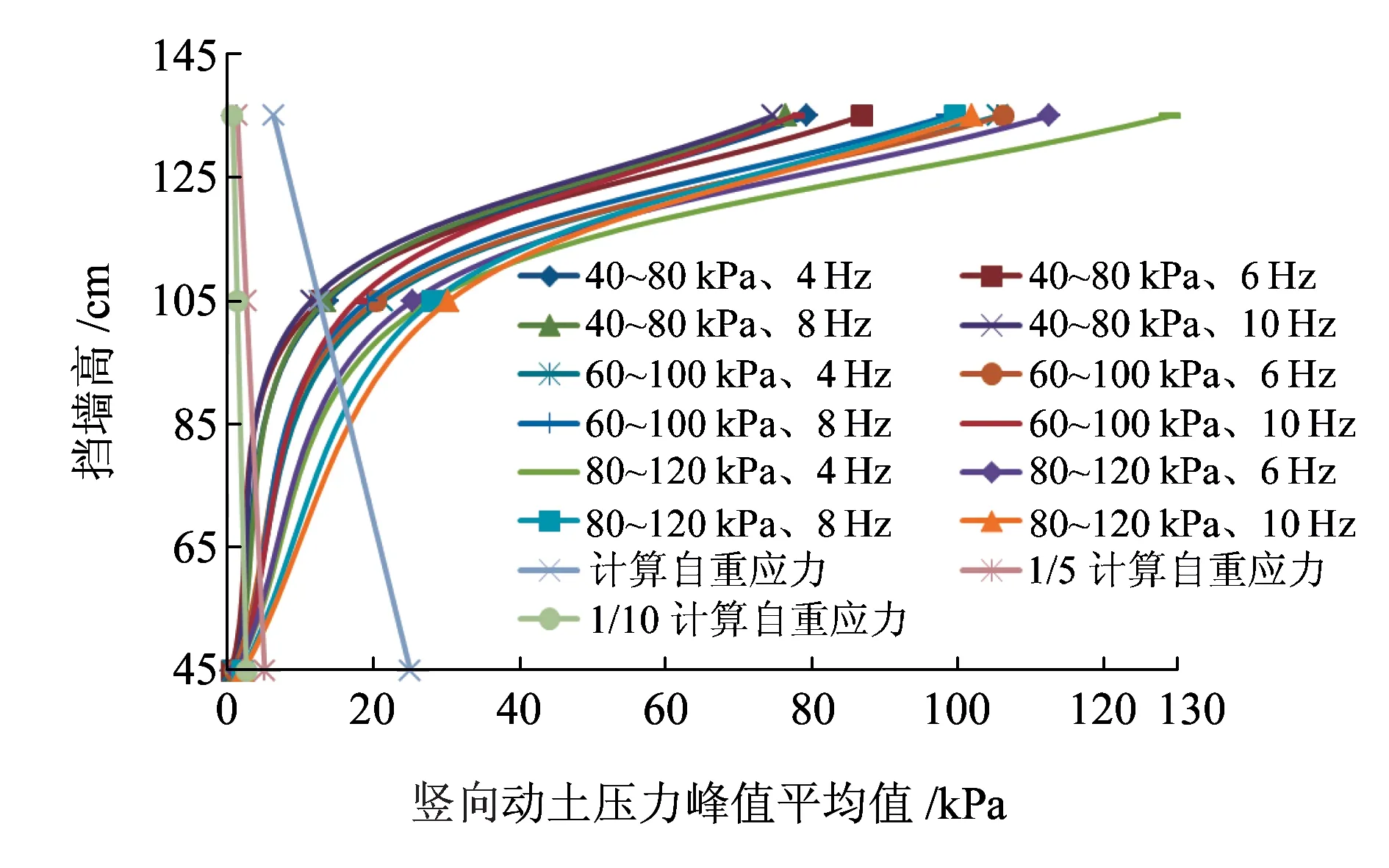
图10 靠近墙面处竖向动土压力沿墙高的分布

3.3.2 水平动土压力分布规律

图11为不同高度层位处水平动土压力峰值平均值随加载频率、次数和加载量的变化情况。从图11可以看出：

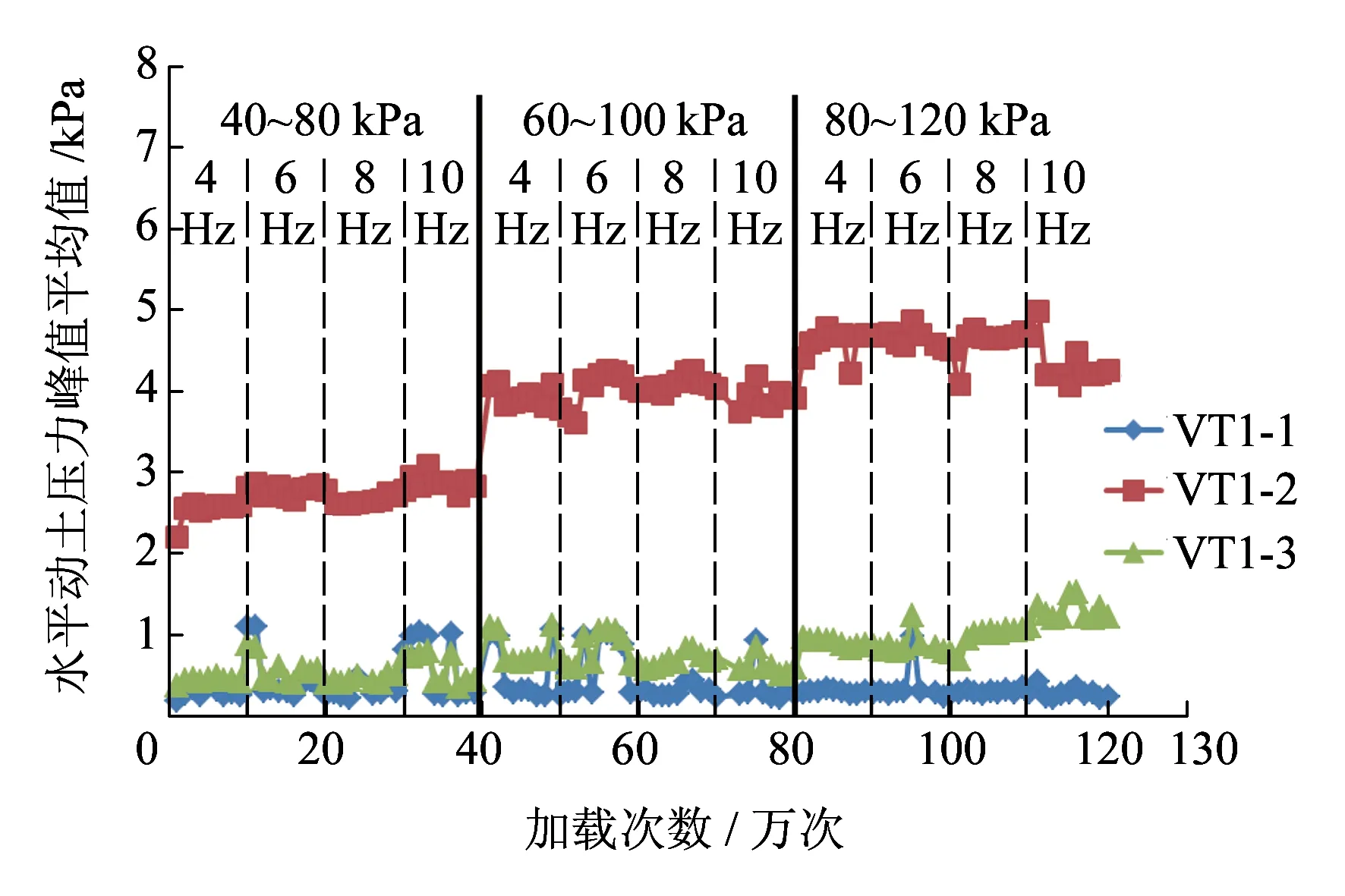
(a)h=0.45 m

(b)h=1.05 m

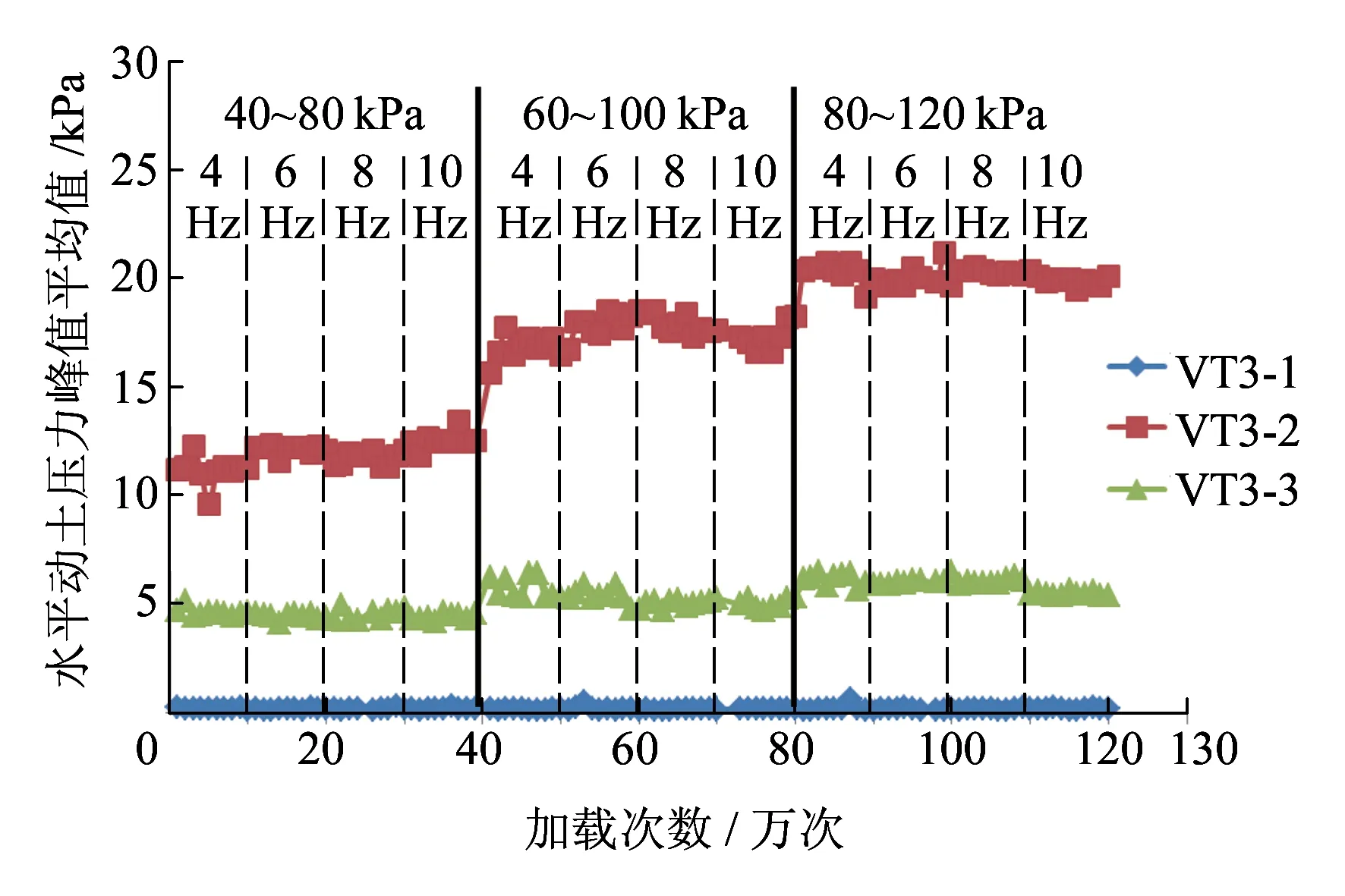
(c)h=1.35 m图11 水平动土压力分布规律

(1)沿筋材方向，水平动土压力最大值出现在加载点附近，分别向筋材末端和墙面两个方向递减，层高越高减小速率越大。同时由于动土应力影响范围从高到低逐步扩大，因此挡墙上部远离加载位置的水平动土压力比下部小。

(2)水平动土压力主要受加载次数和加载大小的影响，受加载频率的影响较小。加载位置下水平动土压力均随加载次数的增加而增大，增长速率逐渐减小；同时，每级加载时动土压力随加载频率的增加略有增长然后趋于稳定。这是由于重复荷载和筋材的共同作用使加筋复合体逐步密实，结构性进一步加强。层高1.05 m处没有明显规律，可能是该处动土压力盒受到了扰动。

(3)靠近墙面处水平动土压力，在0.45 m高度处先增长后趋于稳定；在1.05 m高度处始终处于减小的趋势；在1.35 m高度处随荷载的增加阶段性增长，但在每级荷载加载时间内是减小的。出现上述情况一方面是因为墙面产生了水平位移，部分应力得到释放；另一方面是因为，本来水平动土压力作用就小，同时动土应力的影响作用从高到低逐渐衰减，使影响挡墙底部土体的主要是静载作用，而上部受动载作用大，所以出现了阶段性增长而在每一阶段内却有所减小的趋势。

靠近墙面处水平动土压力沿墙高的分布曲线如图12 所示。由图12可见：水平动土压力沿墙高呈衰减趋势，衰减速率逐渐减小；挡墙高100 cm以上的部分(约为墙高的2/5)承受了约80%由外荷载带来的水平动土压力，100 cm以下部分承受的水平动土压力较小，基本小于1 kPa；因持续加载带来的墙面水平位移使该处水平动土压力出现减小趋势，中下部水平位移较大的部分水平动土压力减小较多。

图12 靠近墙面处水平动土压力沿墙高的分布

3.4 残余土压力分布规律

动载作用在墙体上会引起塑性变形，形成残余土压力。残余土压力定义为挡墙经过动荷载作用后，挡墙内各处静土压力的变化值[10]。为得到挡墙内残余土压力的分布规律，研究不同大小和频率动载对挡墙内静土压力的影响。本试验专门对静土压力数据进行采集，求得其与加载前静土压力之间的差值后进行分析。

3.4.1 竖向残余土压力分布

图13为竖向残余土压力随加载次数、荷载大小和频率的变化情况。由图13可见，竖向残余土压力随加载次数和荷载的增加而增大，其主要影响因素为加载次数和荷载大小，受加载频率的影响较小。这主要是由于残余土压力的增长是缓慢的发展过程，重复不断的作用力才能使强度较高的加筋复合体产生一定的塑性变形，从而形成残余应力。

(a)h=0.15 m

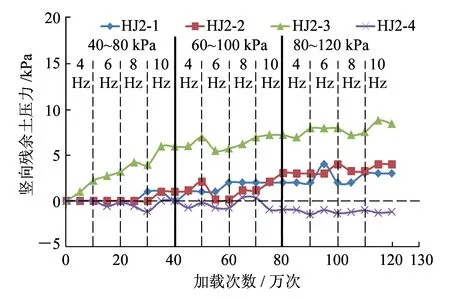
(b)h=0.75 m

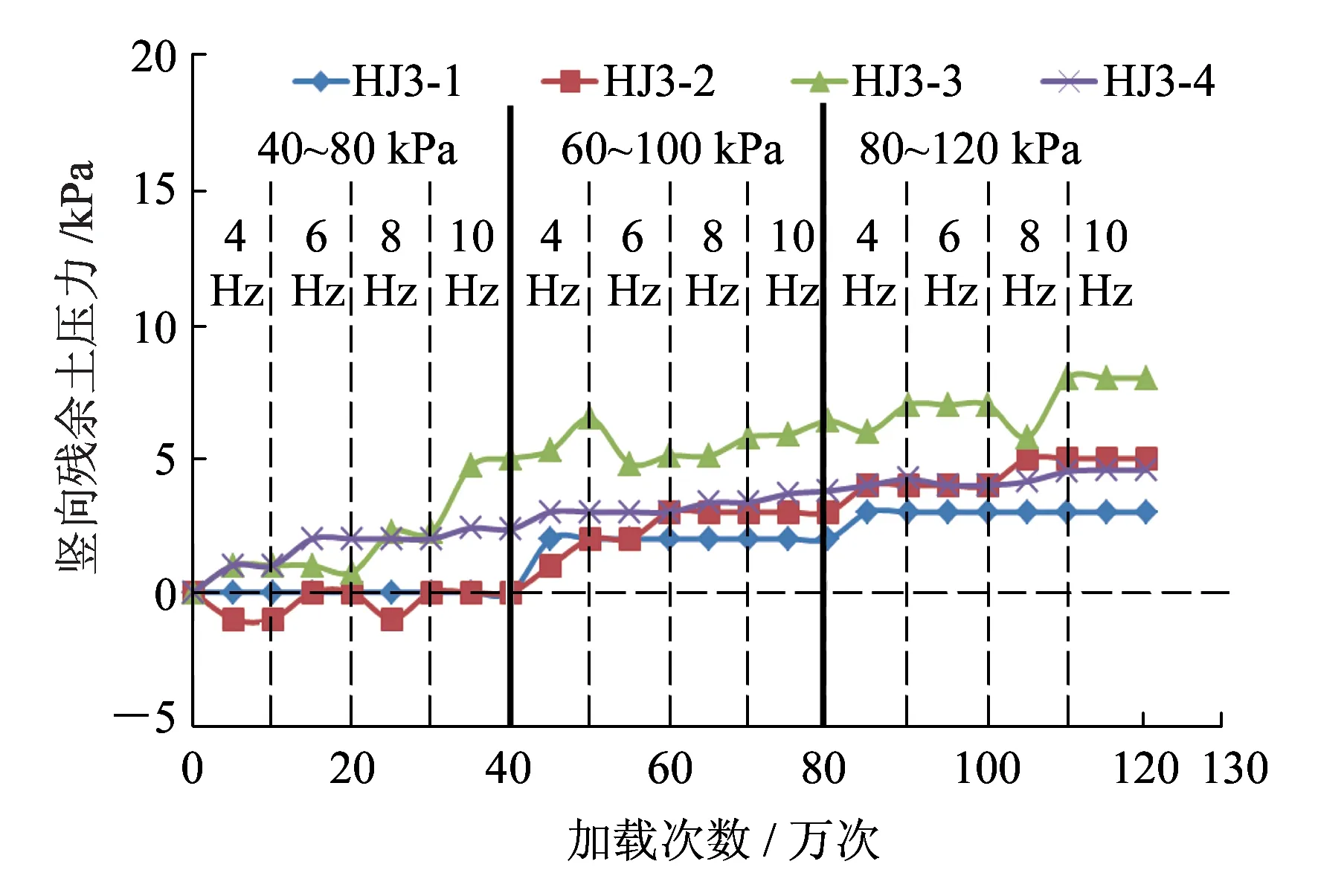
(c)h=1.35 m图13 竖向残余土压力分布

竖向残余应力的增长速率逐渐减小，到一定程度后残余应力趋于稳定。这是因为重复的荷载作用使土体更加密实，达到一定程度后密实度难以继续增加。

在同一荷载区间内竖向残余土压力也有先增后稳的趋势，但较大荷载比较小荷载更快达到本阶段的最大值而趋稳。由此可知，要想达到稳定的残余土压力，可以采用大荷载少次数，也可以采用多次数小荷载的方法。

靠近墙面处的竖向残余土压力的增长较慢、较小，h=0.75 m处甚至出现了负增长。这主要是墙面水平位移的影响，而且墙面中下部水平位移较大。

另外，加载后各处增大后的垂直静土压力沿墙从高到低逐渐增加，可见残余土压力的主要组成是土体自重，动载带来的静土压力增长较小，而且动载的影响作用从高到低逐渐减小。

3.4.2 侧向残余土压力分布

图14为侧向残余土压力在加载过程中的分布。

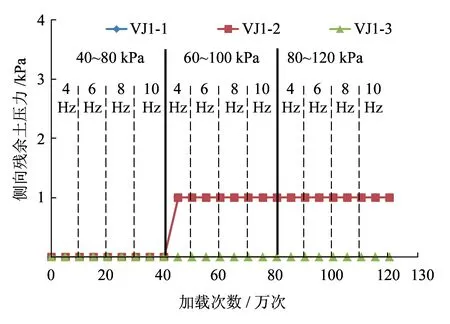
(a)h=0.15 m

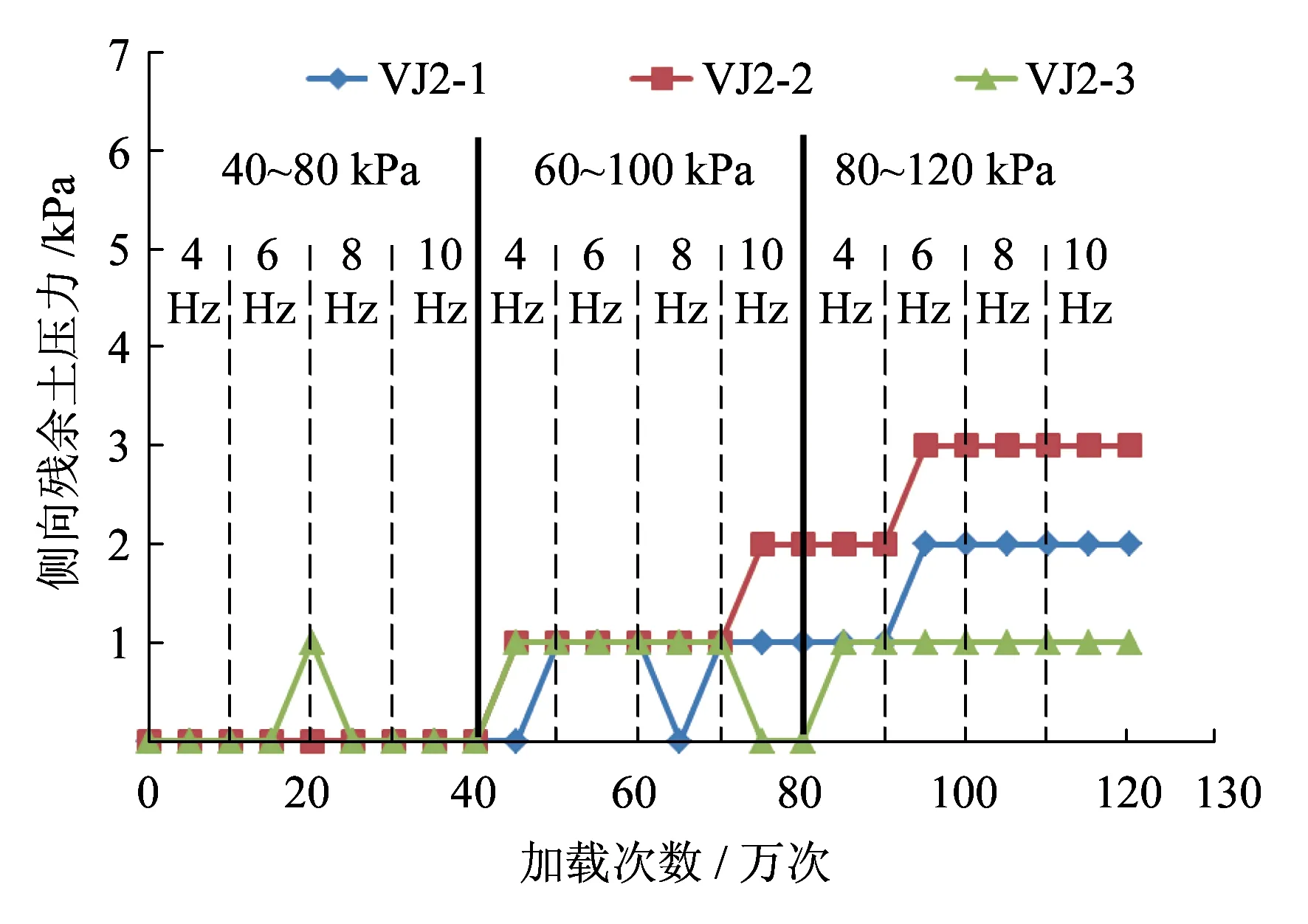
(b)h=0.75 m

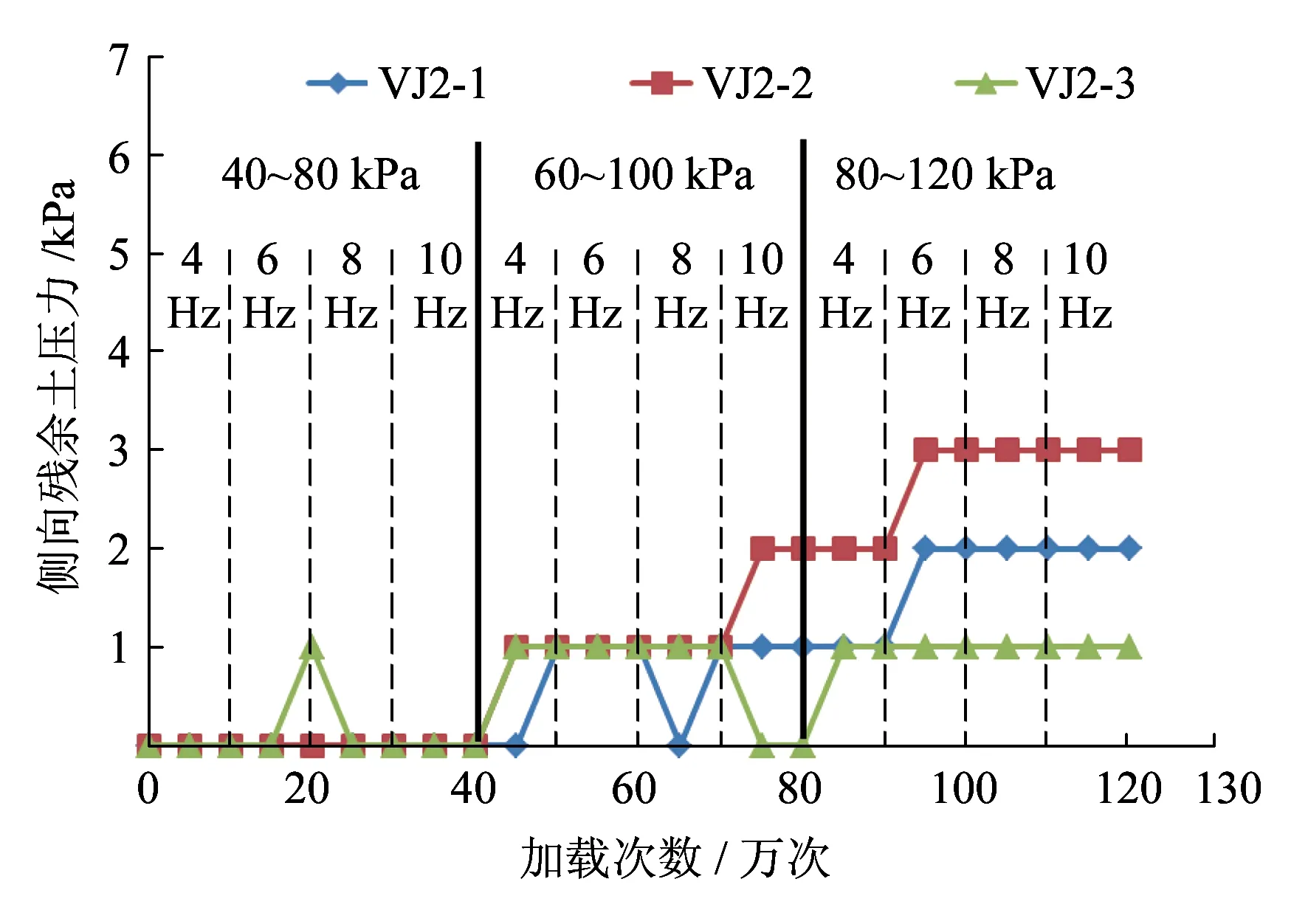
(c)h=1.35 m图14 侧向残余土压力分布

从图14可以看出，动载的重复作用使加筋复合体密实度逐渐达到最大，因此随加载次数和荷载的增加侧向残余土压力呈先增后稳的趋势。其中，靠近墙面处的侧向残余土压力变化不大，主要受墙面水平位移的影响。因中下部墙面位移较大，所以在侧向残余土压力较大的h=0.75 m层，靠近墙面处的残余土压力也较小。

另外，从施加动载后各处增大的水平静土压力来看，挡墙底部受动载作用的影响很小，所以该处土压力没有明显变化；中部受自重应力和动载作用的影响均较大，因此该处土压力较大；上部由于受自重应力影响很小，土压力也较小。

3.5 筋材应变沿筋长的分布

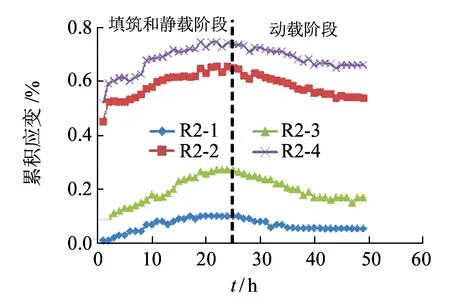
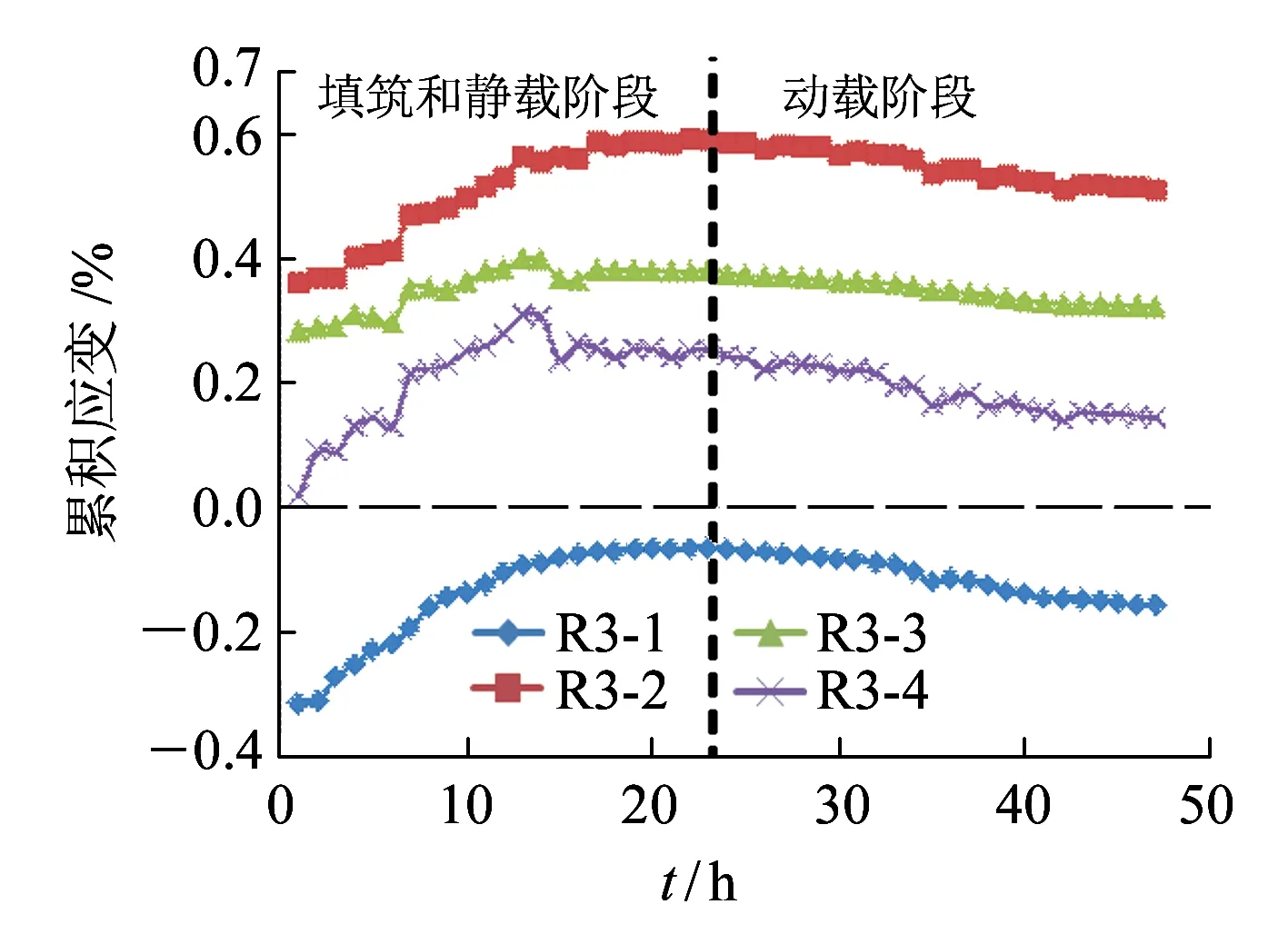
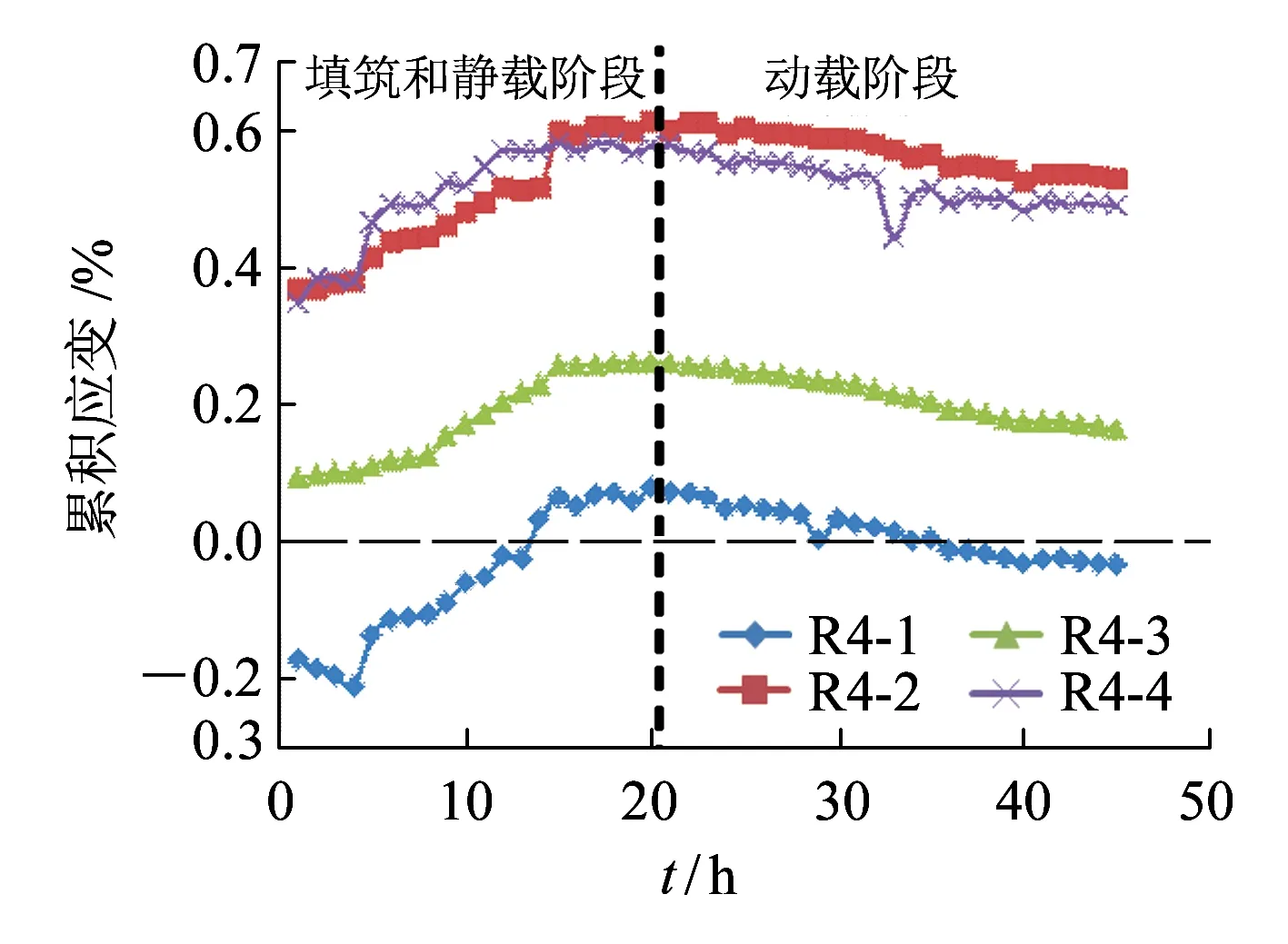
图15为筋材累积应变在填筑-静载-动载整个试验过程中的变化情况(假设以时间为横坐标轴)。

(a)h=0.15 m

(b)h=0.45 m

(c)h=0.75 m

(d)h=1.05 m

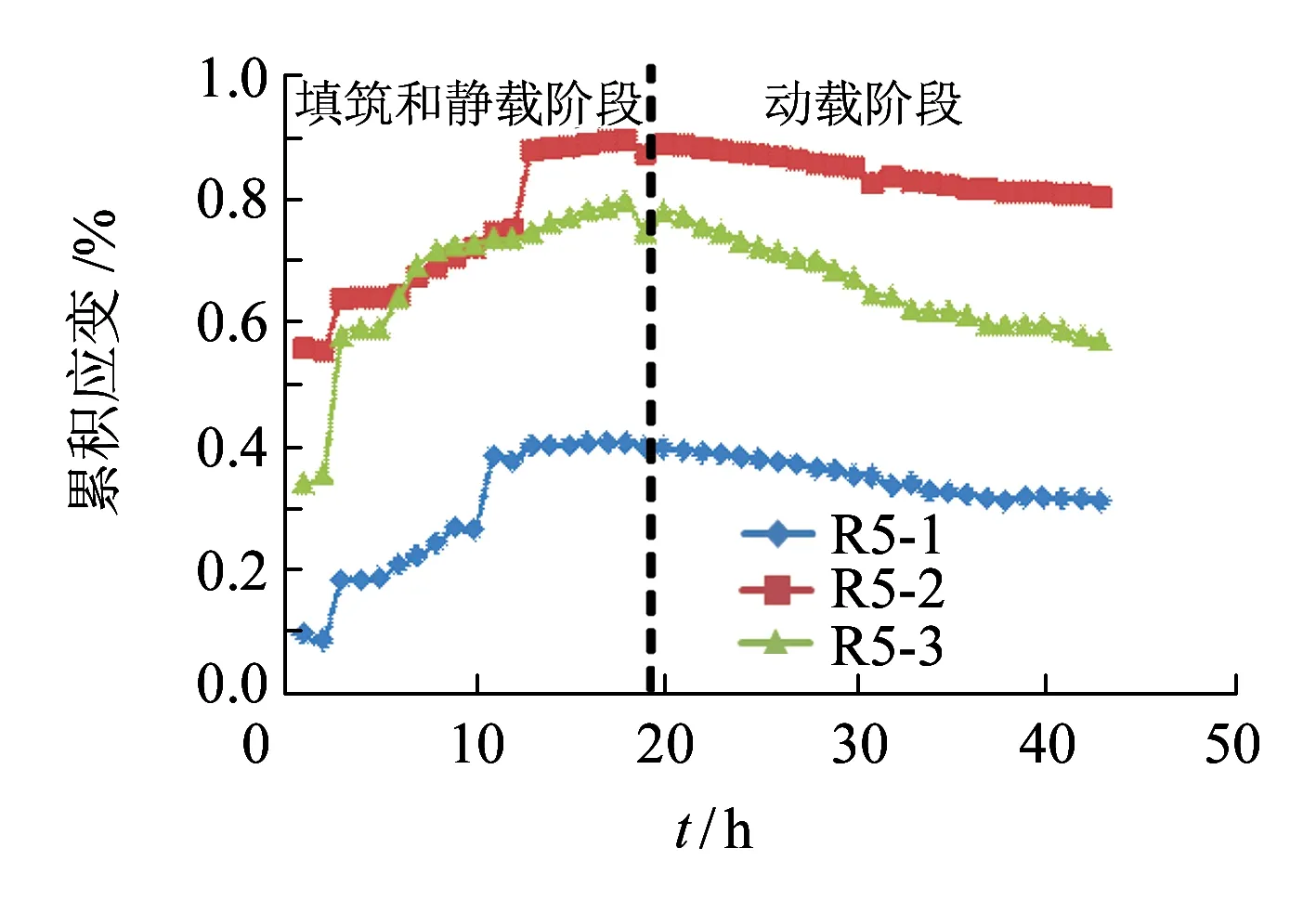
(e)h=1.35 m图15 筋材累积应变随试验进程的分布

从图15可见，筋材累积应变呈增加-稳定-减小-稳定的趋势，增长和减小基本呈线性变化。这说明土工格栅对外加荷载的反应灵敏度较低，拉筋应变控制的关键阶段为施工期。

由于压实夯击能量及土重力作用的影响，筋材累积应变的增长全部出现在填筑期间；施加静力荷载(10～60 kPa)后基本不变，这主要是随荷载增加而增强的土工格栅水平限制作用使水平土压力始终处于较低水平。如果加载范围跨度不大，则很难形成水平土压力较大幅度的增长，从而使得土工格栅应变达到一定值后不再继续发展。

施加动载后，筋材应变降低，而后逐渐趋稳；筋材累积应变的变化几乎不受加载频率和加载大小的影响，受加载次数的影响较大。出现这种情况是因为填筑和静载阶段已经使筋材应变达到一定程度，施加的动载不足以使筋材应变出现进一步增长；同时动力作用使土颗粒重新排列，使筋材具有一定空间产生回弹收缩；随着密实程度的增加，加筋复合体重新形成了稳定结构，从而使筋材应变在降低后逐渐趋于稳定。

拉筋应变在水平方向上基本呈单峰值或双峰值分布，如图16所示。双峰曲线两个峰值出现的原因不同，距墙背较近的峰值出现是墙面水平位移的缘故；另一个峰值的出现是自重应力及土体与拉筋之间摩阻力共同作用的结果。同时可以看出最大值位置(双峰曲线取远离墙面的峰值)从高到低距墙脚水平距离逐渐减小。

从应变值来看，整个试验过程中土工格栅最大累积应变为0.89%(负值出现由不均匀沉降引起的固定柔性位移计两点之间水平距离的减小造成)，占峰值应变的7.74%；施加动载应变稳定后筋材最大累积应变为0.80%，占峰值应变的6.96%。说明拉筋实际受力远小于其抗拉强度值，土工格栅在低于设计值的拉力下变形很小。实际上，实体工程中土工格栅发生的拉伸变形很小，一般均远小于其本身的抗拉强度值。就此来看，土工格栅的强度选取有些保守。

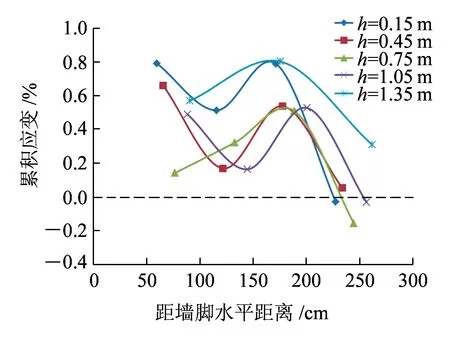
图16 动载筋材累积应变沿筋长的分布

根据以上分析，实际工程中以动载稳定后的应变值为参考较为可靠。

4 结论

根据模型试验结果，墙顶动荷载作用下的返包式土工格栅加筋土挡墙的受力和位移完全满足结构的强度、稳定性、变形和安全的要求，并得到以下结论：

(1)挡墙内加速度受加载频率的影响较大，受加载次数和荷载大小的影响较小。在荷载大小不变的情况下，加速度随频率的增加呈台阶式增长。加载频率为10 Hz时加速度突增，可能接近挡墙的固有频率。

(2)挡墙墙面累积水平位移受荷载变化的影响较大，受加载频率和加载次数的影响较小。每级加载之初位移突然增大，而后逐渐减小趋于稳定。当荷载较大时，墙面累积水平位移才出现明显增加。墙面累积水平位移沿墙高基本呈S形曲线分布。最大值出现部位随荷载的增加逐渐从中部移动到中下部。

(3)墙面累积竖向沉降与加载次数基本线性相关，不受加载频率和荷载大小的影响，其沿墙从高到低呈衰减趋势。

(4)竖向动土压力沿筋材长度方向呈非线性变化，最大值位于加载位置附近，向墙面和筋材末端逐渐减小；受荷载大小的影响较大，受加载频率和加载次数的影响较小；每级荷载加载过程中竖向动土压力先稍有增加而后迅速趋于稳定；靠近墙面位置处动土压力增加较小，在中下部位移较大处甚至略有减小。靠近墙面位置处竖向动土压力沿墙高呈衰减趋势。

(5)水平动土压力沿筋材长度方向呈非线性变化，最大值位于加载位置附近，向墙面和筋材末端逐渐减小；其主要受加载次数和荷载大小的影响，受加载频率影响很小，每级加载后出现短暂增长，很快便趋于稳定。靠近墙面位置处水平动土压力受墙面位移的影响有所减小，中下部减小较多；其沿墙高呈衰减趋势，减小速率逐渐减小；墙高100 cm以上的部分(约为总墙高的2/5)承受了约80%由外荷载带来的水平动土压力，100 cm以下部分承受的水平动土压力基本小于1 kPa。

(6)竖向残余土压力随加载次数的增加而增大，增长速率逐渐减小，其主要受加载值和加载次数的影响。受墙面位移影响，靠近墙面位置处竖向残余土压力增长较慢、较小，甚至出现负增长。动载卸除后，沿墙从高到低静土压力逐渐增加，增长速率逐渐减小。

(7)侧向残余土压力随加载次数的增加呈先增后稳的趋势，靠近墙面处的变化不大。动载卸除后，中部静土压力较大，顶部和底部均较小。

(8)在填筑-静载-动载过程中，土工格栅累积应变呈先增大后减小最后稳定的趋势，减小开始于施加动载后，增长和减小的部分基本呈线性变化。其受加载频率和加载大小的影响很小，主要受加载次数影响。整个试验过程中土工格栅累积应变最大为0.89%，占峰值应变的7.74%；施加动载应变稳定后筋材最大累积应变为0.80%，占峰值应变的6.96%，均远小于筋材的抗拉强度。水平方向上各层土工格栅应变分布规律一致，但层间不同，基本为单峰或双峰曲线，峰值出现位置(双峰曲线取远离墙面处)从高到低距墙脚水平距离逐渐减小。

参考文献：

[1]GÖBEL C H,WEISEMANN U C.Effectiveness of a Reinforcing Geogrid in a Railway Subbase under Dynamic Loads[J].Geotextiles and Geomembranes,1994,13(2):91-99.

[2]MAHER M H,WOODS R D.Dynamic Response of Sand Reinforced with Randomly Distributed Fibers[J].Journal of Geotechnical Engineering,1990,116(7):1 116-1 131.

[3]AOYAMA N,KIKUCHI N,KONAMI T,et al.Actual Size Vibration Test on the Multi-anchored Retaining Walls with Large Scale Shear Box(Part 1)[C]//Proceedings of 35th Geotechnical Engineering Conference.Gifu,Japan,2000:2 213-2 214.

[4]FUTAKI M,MISAWA K,TATSUI T.Actual Size Vibration Test on the Multi-anchored Retaining Walls Large Scale Shear Box(Part 2)[C]//Proceedings of 35th Geotechnical Engineering Conference.Gifu,Japan,2000:2 215-2 216.

[5]LIU Huabei,YANG Guangqing,LING HoeI.Seismic Response of Multi-tiered Reinforced Soil Retaining Walls[J].Soil Dynamics and Earthquake Engineering,2014(61-62):1-12.

[6]杨果林，李海深，王永和.加筋土挡墙动力特性模型试验与动力分析[J].土木工程学报,2003,36(6)：105-110.

YANG Guolin,LI Haishen,WANG Yonghe.Model Test on Reinforced Earth Retaining Wall under Repeated Load[J].China Civil Engineering Journal,2003,36(6):105-110.

[7]杨果林,肖宏彬,王永和.加筋土挡墙动变形特性试验与疲劳损伤分析[J].振动工程学报,2002,15(2):173-177.

YANG Guolin,XIAO Hongbin,WANG Yonghe.Experiment Dynamic Behaviour and Analysis of Fatigue Damnify of Reinforced Earth Wall[J].Journal of Vibration Engineering,2002,15(2):173-177.

[8]杨果林,王永和.加筋土挡墙在重复荷载作用下的模型试验与动态响应分析[J].岩石力学与工程学报,2002,21(10)：1 541-1 546.

YANG Guolin,WANG Yonghe.Model Testing and Dynamic Response Analysis on Reinforced Earth Wall under Repeated Load[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(10):1 541-1 546.

[9]杨果林，王永和.土工合成材料在加-卸循环荷载作用下的应力-应变特性研究[J].铁道学报,2002,24(3):74-77.

YANG Guolin,WANG Yonghe.Study on Stress-strain Relationship of Geosynthetics under Cyclic Loaded-unloaded[J].Journal of the China Railway Society,2002,24(3):74-77.

[10]李昀.格宾加筋挡土墙动力特性试验研究及数值分析[D].长沙：中南大学,2010.

[11]蒋建清,邹银生.动力作用下加筋土挡墙的数值模拟[J].湖南城市学院学报:自然科学版,2006,15(4):12-14.

JIANG Jianqing,ZOU Yinsheng.Numerical Simulation of Reinforced Retaining Walls under Dynamic Loads[J].Journal of Hunan City University:Natural Science,2006,15(4):12-14.

[12]李海深,杨果林,邹银生.加筋土挡土墙动力特性分析[J].中国公路学报,2004,17(2):28-31.

LI Haishen,YANG Guolin,ZOU Yinsheng.Analysis of Dynamic Character of Reinforced Earth Retaining Wall[J].China Journal of Highway and Transport,2004,17(2):28-31.

[13]蒋红光,边学成,徐翔,等.列车移动荷载下高速铁路板式轨道路基动力性态的全比尺物理模型试验[J].岩土工程学报,2014,36(2)：354-362.

JIANG Hongguang,BIAN Xuecheng,XU Xiang,et al.Full-scale Model Tests on Dynamic Performances of Ballastless High-speed Railways under Moving Train Loads[J].Chinese Journal of Geotechnical Engineering,2014,36(2):354-362.