铁路集装箱班列动态舱位控制策略研究
张小强,庄乾秋,陈 宇,刘 丹
(1.西南交通大学 交通运输与物流学院,四川 成都 610031;2.西南交通大学 经济管理学院,四川 成都 610031)
目前,中国铁路集装箱运输与发达国家铁路集装箱发展水平相比,仍然存在着较大差距。铁路集装箱发送量在全国铁路货运量中所占的比例不到3%,远远低于发达国家30%~40%的比例。因此铁路集装箱运输是未来铁路货运发展的重要方向,也是提升铁路货运效益的重要途径。近年来中国铁路货运总量逐年下滑,铁路集装箱运输也受到越来越多的挑战。单一的价格和舱位控制策略影响了铁路集装箱货物运输的发展。多年来,我国铁路集装箱运输管理方案定性原则多、定量计算少。面对来自航空、公路和水运的激烈竞争,集装箱运输作为铁路货物运输的主要发展方向,需要引进科学的管理手段,提高管理水平和服务质量,优化集装箱舱位分配与价格管理策略,实现公平原则上有限运力的收益最大化。针对铁路集装箱运输中出现的问题,本文应用收益管理理论,根据市场需求及竞争情况,建立收益优化模型,研究动态舱位价格控制策略,以期提高铁路集装箱运输业务的竞争力和盈利能力。
收益管理已经成为航空领域以及其他服务业提高收益的重要管理工具。国内对铁路货运收益管理方面研究不足,主要原因是过去铁路货运价格由发改委制定和发布,全路采用固定价格策略。另外铁路货物运输组织相对复杂,使得研究人员必须具备一定铁路运输组织知识才能开展研究。当前我国铁路货运市场化改革正在积极推进:不断开发新的货运产品,满足市场需求;利用电子商务实现网上下单;各铁路局对部分运输产品自主定价等。
在我国宏观经济下行压力加大、大宗有效货源低迷、零散白货市场竞争加剧的情况下,铁路集装箱运输不仅承担铁路运输自然增长的货运量,还将承担从公路转向铁路的货运量。面对来自铁路快捷运输市场不断增长的多样性需求,铁路货运部门应积极探索集装箱营销策略,在满足客户需求的同时,发挥一切资源优势,增加运量,提高收益。因此铁路集装箱运输实行收益管理及不同等级价格舱位管理变得更加迫切。基于收益最大化目标,对不同价格的集装箱舱位进行容量控制,优先满足高价舱位的需求,剩余部分由低价舱位需求进行补充。
1 研究综述
舱位控制最早起源于航空客运,也是目前研究和应用比较成熟的领域。舱位控制作为收益管理的重要技术之一,主要解决的问题是在产品或服务预定期间是接受还是拒绝顾客在某一时刻对某一类产品或服务的预定请求。根据决策过程的实时更新变化情况,可将舱位控制分为静态舱位控制和动态舱位控制。在动态舱位控制方面,以Talluri and Van为代表的团体研究成果较多。他们研究了动态舱位控制模型,并给出网络动态舱位控制的一些近似求解方法,指出虽然竞价控制在一般情况下不是最优的策略,但是随着航段数和容量的增加,竞价控制可以达到近似最优[1-3]。此外,Talluri and Van还研究了考虑顾客选择行为的离散时间动态舱位控制策略[4]。文献[5]研究了连续时间的动态座位控制策略,模型本身考虑了不同票价等级的座位嵌套问题。文献[6]假设舱位预定请求服从相互独立的非齐次泊松分布,并提出了一种网络动态容量控制的最优求解方法。文献[7]研究了单航段离散时间的动态舱位控制,分别研究了单个订舱请求和多个订舱请求的情况,但文章并没有涉及到多航段情况。文献[8]在文献[7]的基础上研究了多航段动态舱位控制,为了解决模型求解过程中的“高维”特性,用指数形式的参数化函数代替期望收益函数进行求解,并通过算例表明该方法比较接近最优解。文献[9]分析了多航段座位控制中竞价的单调性,指出在多航段中由于各航段的容量不平衡,各个运行区间的竞价不一定都是单调的。
在铁路货运收益管理方面,文献[10]基于铁路运输组织的特点,分析了铁路货运收益管理的复杂性,并以铁路整车和联合运输为例,建立了适用于铁路货运的收益管理模型。文献[11]认为铁路货运是一个多产品网络运输问题,并采用竞标竞价策略研究了该问题。文献[12]将铁路运营计划和铁路集装箱收益管理相结合,提出了一种新的双层数学模型,该模型涵盖了定价、网络计划以及列车编组调度等。
与航空货运和海运集装箱相比,铁路集装箱动态舱位控制的研究目前刚刚起步。文献[13,14]分别研究了航空货运和海运集装箱单航段动态舱位控制,但是都没有扩展到多航段的情况。由于铁路货运途中经过的站点较多,属于线型网络运输,因此本文研究铁路集装箱多站段动态舱位控制,并通过竞标价格控制舱位预定过程,比较分析加和竞价与确定性等价控制两种策略对总收益的影响。
2 多站段动态舱位控制模型
2.1 符合假设与说明
模型假设:
(1)班列的舱位(一个舱位等同于一个标准集装箱)数固定,不考虑空车调运,不考虑预定取消和No-show;
(2)预定到达服从非齐次泊松过程,并且需求相互独立;
(3)每个决策阶段至多有一个顾客预定到达,并且每个到达的顾客只定一个舱位。
符号说明:
t=1,…,T表示决策阶段(t=0代表列车开行,t=T代表舱位预定开始);
i=1,2,…,m表示列车运行中经过的站段数;
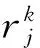
A=[aij]表示起讫点OD对路段的占用矩阵,若aij=1说明i路段被jOD占用,否则aij=0。定义Ai是矩阵A的第i行,表示路段i,Aj是A矩阵的第j列,表示jOD对路段占用情况。向量x=(x1,…,xm)是状态变量,表示剩余舱位数,如果接受了jOD区间的舱位预定请求,则状态变量变为x-Ai。当每个OD可以运输K类货物时,则占用矩阵A有K列相同的Aj,此时A是m×nK维的矩阵。
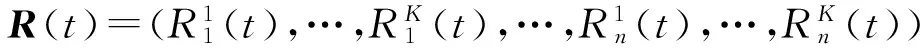

μ(x)={μ∈(0,1):Aμ(t)≤x}
2.2 模型创建
用Vt(x)表示t时间段,剩余舱位数为x时的最大期望收益,则Vt(x)满足Bellman
Vt-1(x-Aμ(t))}]
( 1 )
式中,R(t)T是随机需求矩阵R(t)的转置,模型的边界条件是
VT(x)=0 ∀x
Vt(0)=0t=1,…,T
( 2 )
式( 2 )表明,有可利用的剩余舱位时,某个舱位预定请求的运价必须满足式( 3 ),才接受该预定,否则拒绝。
( 3 )
Vt-1(x)-Vt-1(x-Aj)就是t决策阶段,剩余舱位为x时,jOD运输路径的机会成本。
3 模型转化分析

s.t.
A·y≤x
( 4 )
0≤y≤E[Dt]
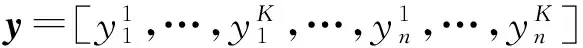
3.1 加和竞标价格
由于线性规划问题的对偶解就是资源的机会成本。所以式( 4 )在约束条件下求得的对偶解就是各站段的竞价,模型( 4 )的对偶问题是
s.t.
v·A+u≥r
( 5 )
u,v≥0
其中,向量u,v为t决策阶段剩余舱位为x时对偶问题的变量,记(vx,t,ux,t)′为(x,t)状态时对偶问题的最优对偶解,则jOD的竞价为其所占用的所有站段的竞价进行加和求得,即
BPj(x,t)=(vx,t)′·Aj
由此可以看出,jOD的竞价取决于对偶变量最优解的结构。文献[15]指出这种基于站段加和竞价的主要缺点是:对偶解可能不是唯一确定的,可能会有多个最优解,而且这种方法也没有考虑运价等级间的嵌套;其次就是在接受团体预定和占用多个站段的OD运输请求时,对偶基不能随之相应地改变。
3.2 确定性等价控制
确定性等价控制是属于近似动态规划方法中的一种,是指最优值函数由线性规划的松弛函数代替,线性规划的松弛方法是指放松对自变量的整数约束,则t决策阶段jOD的机会成本,由最优函数值通过计算得到。
( 6 )
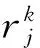
3.3 两种策略的比较分析

=(vx,t)′·x+(ux,t)′·Dt-1-{(vx-Aj,t)′·
(x-Aj)+(ux-Aj,t)′·Dt-1
( 7 )

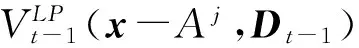
(x-Aj)+(ux,t)′·Dt-1
( 8 )
( 9 )
由此可以看出,确定性等价控制确定的竞价大于或等于加和竞价下的竞价,也就是说如果确定性等价策略接受了jOD的舱位预定请求,则在加和竞价策略下也是接受的,但是反之不一定成立。
4 算例分析
本文选取由广东佛山发往浙江海宁的集装箱快运班列为背景案例。该班列是广铁集团为满足广州及周边的白货(主要货源为日用品、日用电器、配件等)发往浙江及周边地区的需求开行的集装箱货运班列。该班列于2015年6月18开始试运行,货运需求稳步增长。在开行初期,每周开5列,每列30车。经过2个多月的市场培育,从2015年9月1日起每周开6列,每列开行45车。假设中间只停靠南昌站和金华西站,运行路线如图1所示,三个站段最大舱位(集装箱)数分别是45、30和12。

图1 佛山到海宁的集装箱货运班列
根据非齐次泊松分布过程的性质,可将舱位预定时间大致分为1 370个决策阶段。首先对舱位预订的前期、中期和舱位预订将要结束时,剩余舱位分别为(42,28,10)、(20,12,5)和(2,3,1)时两种策略下的竞价进行对比分析,取t为1 300、600和100分别代表舱位预订的前期、中期和后期。用Matlab R2013a编程求解,可求得t决策阶段,剩余舱位为x时两种策略下的竞价,见表3~表5。

表1 舱位预定期内的需求均值
注:表中“1~10”表示舱位预定时间还剩10 d,以此类推。
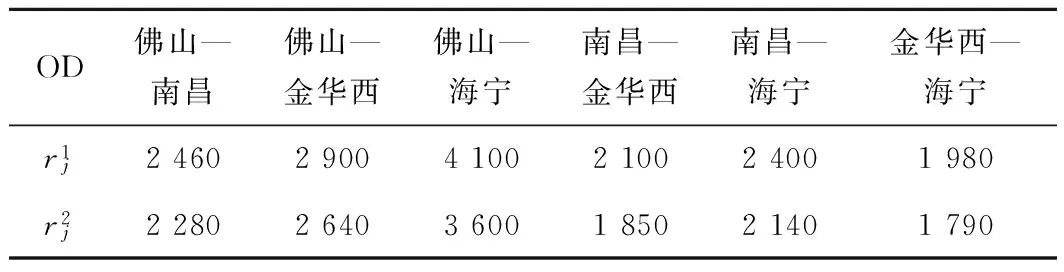
表2 各OD间两类货物的集装箱运价 元
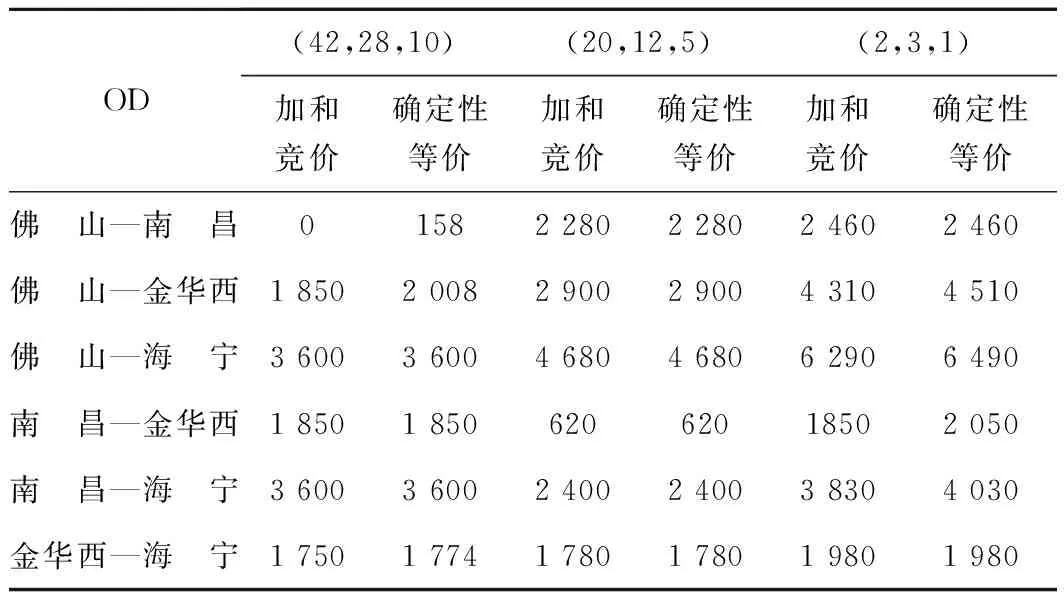
表3 t=1 300时,各OD的竞价 元
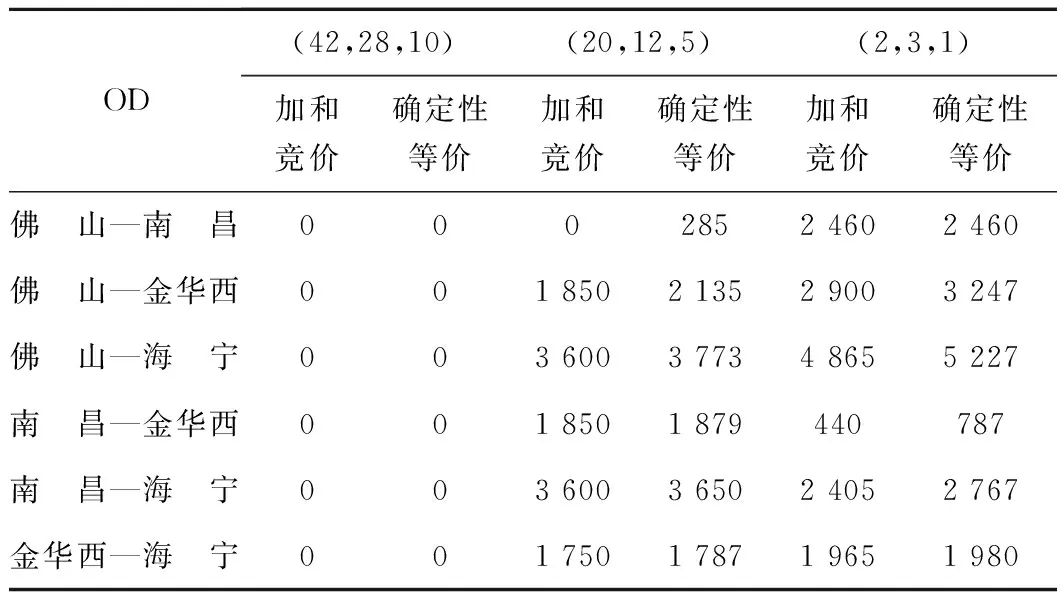
表4 t=600时,各OD的竞价 元
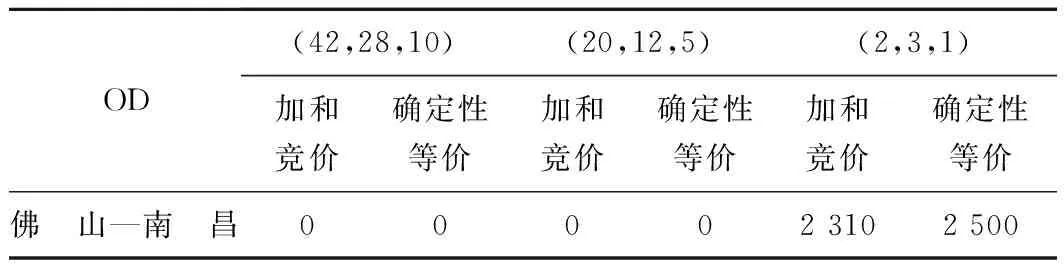
表5 t=100时,各OD的竞价 元
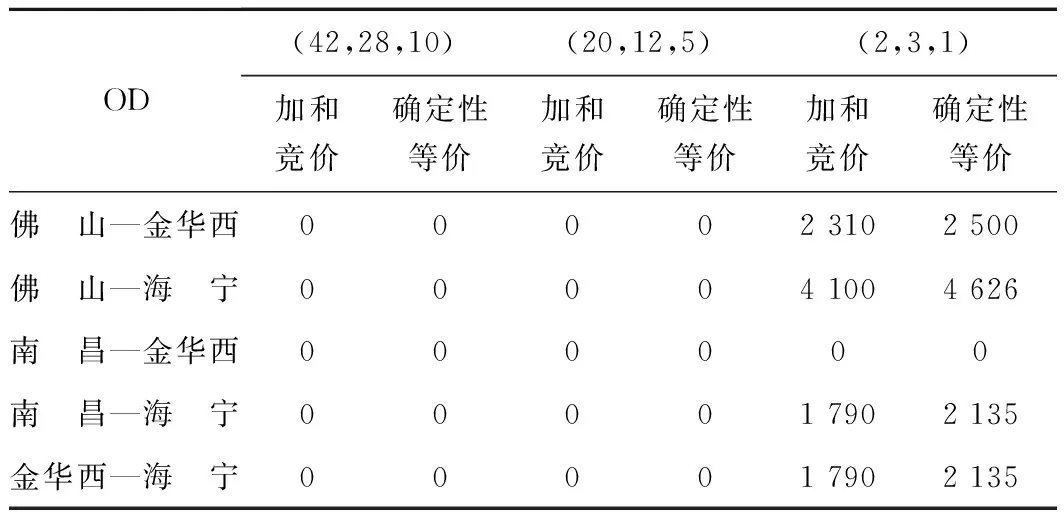
续上表
由表中数据可以得出以下结论:
(1)在两种控制策略下,各OD的竞价基本上都是随着剩余舱位的减少而增大,表明在剩余舱位不多的情况下,货主或顾客要想预定舱位完成货物运输就要支付较高的运价。
(2)在接近班列开行时(表5),不同的剩余舱位情况下,各OD的竞价有明显的不同:当剩余舱位较多,即舱位供应充足时,竞价甚至是零,也就是说在接近班列开行时,如果舱位剩余较多,只要有预订请求就要接受,宁可将舱位以低价售出也不让舱位虚耗;如果剩余舱位较少,即舱位供给紧张时,就要有选择性的接受预定请求,尽可能将舱位以高价售出,保证舱位的高收益。

表6 两种策略下的期望收益 元
表6是在剩余舱位数量不同时,两种策略计算得到的最大期望收益,可以看出确定性等价控制获得的期望收益高于加和竞价策略。
图2~图4分别是剩余舱位为(42,28,10)、(20,12,5)和(2,3,1)时,两种控制策略下各OD区间的竞价随着剩余决策阶段t的变化。可以看出:在剩余舱位一定时,两种控制策略下各OD区间竞价曲线的总体趋势是一致的,而且多数OD区间的竞价是决策时间段的单调非减函数,也有个别OD的竞价是非单调的,这是因为各站段的舱位数不平衡造成的。例如在剩余舱位为(2,3,1)时,如果售出了金华西—海宁的舱位,剩余舱位变为(2,3,0),那么佛山—海宁、南昌—海宁就没有可利用的舱位。由于接近班列开行时,每个预定请求都非常有价值,如果后来的客户因为售出了金华西—海宁的舱位而订不到舱,就要售出更多占用佛山—南昌、南昌—金华西两个站段的订舱请求,才能将所有舱位售出。所以,在集装箱班列运输的动态舱位控制中,各OD的竞价不一定是单调的,其变化趋势要根据具体情况而定。当需求比较高的时候,集装箱运输的竞价就会更高,如果需求不足的时候,竞价就会降低。

(a)加和竞价
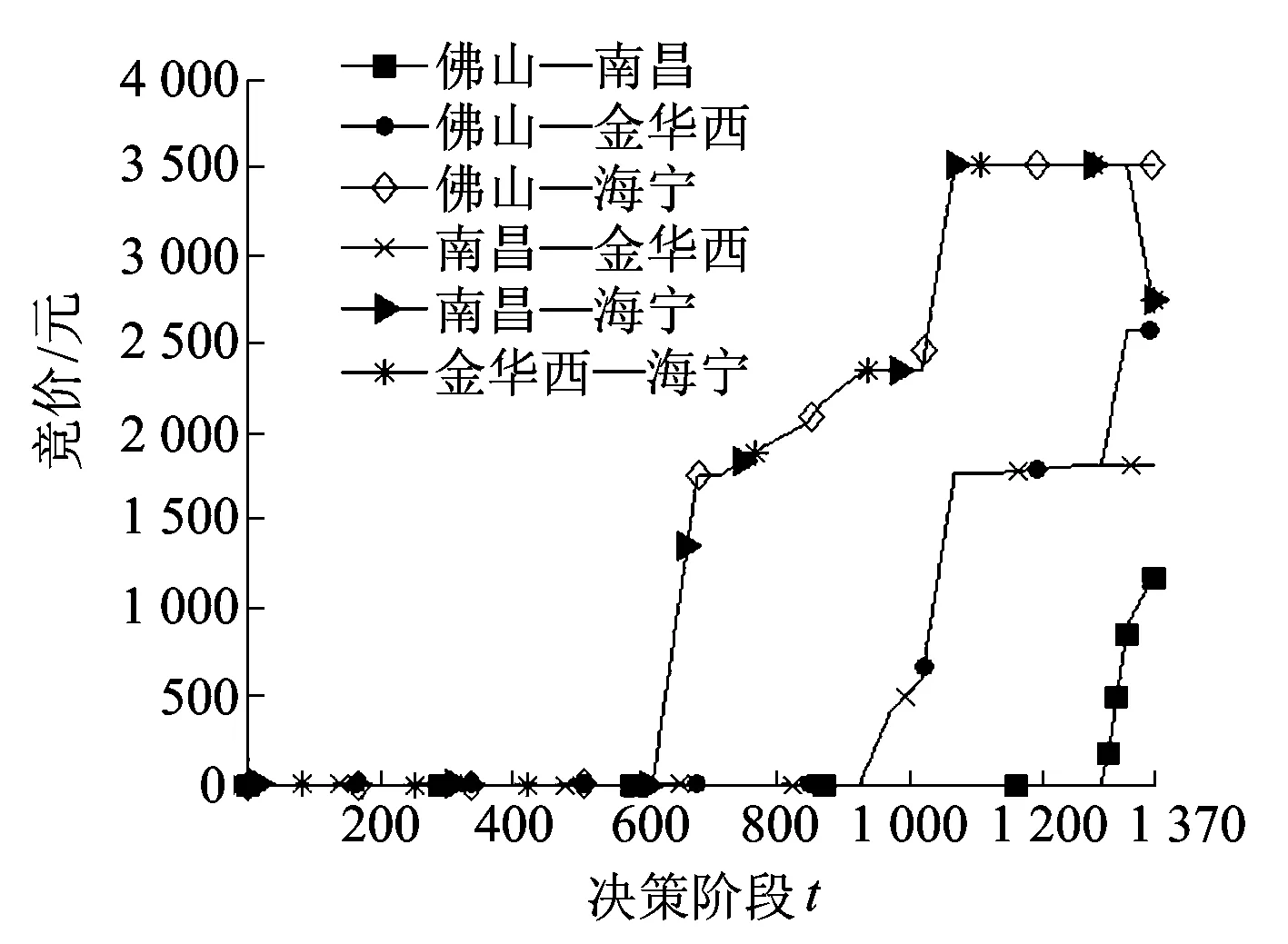
(b)确定性等价图2 剩余舱位x=(42,28,10)时,各OD区间竞价随t的变化

(a)加和竞价
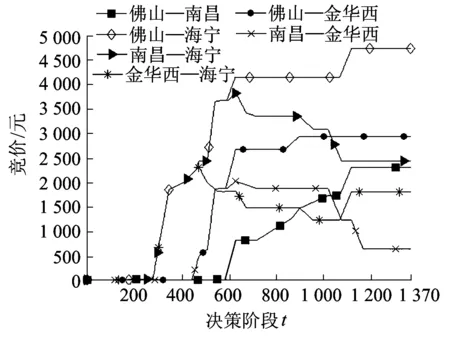
(b)确定性等价图3 剩余舱位x=(20,12,5)时,各OD区间竞价随t的变化
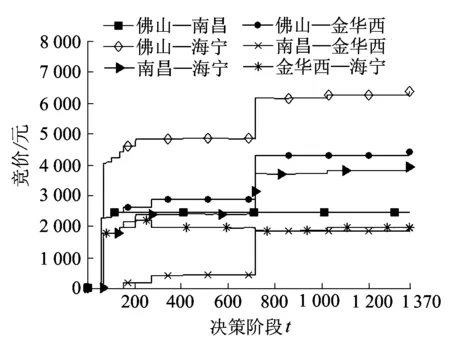
(a)加和竞价

(b)确定性等价图4 剩余舱位x=(2,3,1)时,各OD区间竞价随t的变化
通过这个模型可以实时计算当前情况下应该接受哪个价位的订单。通过这个策略,最终可以在不增加成本的前提下,提高铁路运输企业的收益。这也是未来铁路进一步对价格进行改革的方向。
5 结束语
本文针对目前我国铁路部门在货运改革中急需解决的价格和舱位控制问题,研究铁路集装箱多区间多级运价的动态舱位控制策略。比较分析了加和竞价策略和确定性等价控制策略,通过实例论证了确定性等价控制策略不仅能够保证舱位的高收益,而且在剩余舱位和决策阶段发生变化时,多数情况下能够相应地改变接受和拒绝舱位预订请求的阈值,整体上要优于加和竞价策略。确定性等价方法可以用于铁路公司对集装箱班列运输的价格和舱位分配控制,该方法能够在不增加企业的额外成本情况下提高运输收益。
文章假定需求是已知的,但是往往需求是由市场竞争决定的。因此后续的研究将考虑价格和需求之间的关系。此外,空箱调运是铁路集装箱运输的重要环节,因此后续还将研究基于空箱调运成本最优的铁路集装箱动态舱位控制策略。
参考文献:
[1]TALLURI K,Van Ryzin G.A Randomized Linear Programming Method for Computing Network Bid Prices[J].Transportation Science.1999,33(2):207.
[2]TALLURI K,Van Ryzin G.An Analysis of Bid-price Controls for Network Revenue Management[J].Management Science,1998,44(11):1 577-1 593.
[3]Kalyan Talluri,Garrett Van Ryzin,Itir Karaesmen,et al.Revenue Management:Models and Methods[C]//IEEE.Proceedings of the 2009 Winter Simulation Conference.Austin,Texas,USA,2009:148-161.
[4]Talluri Kalyan,Van Ryzin Garrett.A Disceret Choice Model of Yield Management[J].Ssrn Electronic Journal,2001.
[5]FENG Y,XIAO B.A Dynamic Airline Seat Inventory Control Model and Its Optimal Policy[J].Operations Research,2001,49(6):938-949.
[6]WANG X,WANG F.Dynamic Network Yield Management[J].Transportation Research Part B:Methodological,2007,41(4):410-425.
[7]LEE T C,HERSH M.A Model for Dynamic Airline Seat Inventory Control with Multiple Seat Bookings[J].Transportation Science,1993,27(3):252.
[8]HUANG K,LIANG Y.A Dynamic Programming Algorithm Based on Expected Revenue Approximation for the Network Revenue Management Problem[J].Transportation Research Part E:Logistics and Transportation Review,2011,47(3):333-341.
[9]LI J.Dynamic Seat Allocations for Network Revenue Management in the Airline Industry[D].Texas A&M University,2000.
[10]CAMPBELL K E.Rail Freight Service Flexibility and Yield Management[J].Transportation Research Forum Proceedings,1994,2(3):529-548.
[11]KRAFT E R.Scheduling Railway Freight Delivery Appointments Using a Bid Price Approach[J].Transportation Research Part A,2002,36(2):145-165.
[12]CREVIER B,CORDEAU J,SAVARD G.Integrated Operations Planning and Revenue Management for Rail Freight Transportation[J].Transportation Research Part B,2012,46(1):100-119.
[13]桂云苗,朱金福.航空货运动态舱位控制模型研究[J].预测,2007(6):53-56.
GUI Yunmiao,ZHU Jinfu.Research on Dynamic Model of Air Cargo Slot Inventory Control[J].Forecasting,2007(6):53-56.
[14]卜祥智,赵泉午,武振业.海运集装箱收益管理舱位动态控制策略研究[J].中国管理科学,2006(14):56-60.
BU Xiangzhi,ZHAO Quanwu,WU Zhenye.Study on Dynamic Space Control Strategy of Container Shipping Revenue Management[J].Chinese Journal of Management Science,2006(14):56-60.
[15]BERTSIMAS D,POPESCU I.Revenue Management in a Dynamic Network Environment[J].Transportation Science,2003,37(3):257-277.

