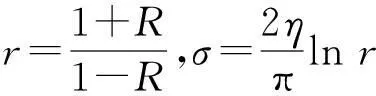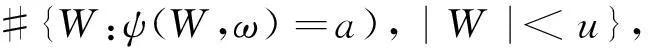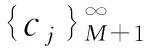全平面上q-级随机Dirichlet级数的Borel线

李云霞

(楚雄师范学院 数学与统计学院, 云南 楚雄 675000)



全平面上q-级随机Dirichlet级数的Borel线

李云霞

(楚雄师范学院 数学与统计学院, 云南 楚雄 675000)

摘要：研究由全平面上收敛的q-级随机Dirichlet级数表示的整函数F(s,ω)的值分布性质,得到了q-级随机Dirichlet级数表示的整函数几乎必然(a.s.)每条水平直线是F(s,ω)的没有有限例外值的q-级Borel线.

关键词：随机Dirichlet级数; q-级; Borel线

1预备知识与主要结果

Dirichlet级数表示的整函数的增长性和值分布是复分析的重要研究方向之一,是由S. Mandelbrojt[1]及G. Valiron[2]首先研究的.相关的研究被推广到更一般的随机Dirichlet级数的情形,文献[3-5]在这方面做了重要工作.对于随机Dirichlet级数表示的整函数,在文献[1-5]中介绍了一些关于整函数的系数、级及值分布的有趣结果,文献[6-8]中分别讨论了随机Dirichlet级数表示的整函数的无穷级和零级的Borel线.本文在文献[9-17]的基础上进一步完善他们的结果,讨论对于独立、非同分布的随机Dirichlet级数表示的整函数F(s,ω)的值分布问题,获得了几乎必然(a.s.)每条水平直线是F(s,ω)的没有有限例外值的q-级Borel线,推广了文献[6-8]中随机Dirichlet级数表示的整函数的值分布的结果.

考虑辅助Dirichlet级数

(1)

其中,{an}⊂C,0<λn↑∞,s=σ+it(σ,t为实变量).另外,设级数(1)满足

(2)

由条件(2)和Valiron公式[2],Dirichlet级数(1)的一致收敛横坐标为-∞,则F(s)定义了一个全平面收敛的整函数.

令

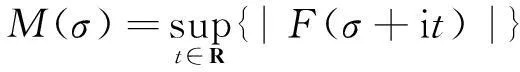
表示F(s)的最大模.另记exp[0]x=ln[0]x=x;当k>1,

ln[k]x=ln(ln[k-1]x).

Dirichlet级数q-级ρ的定义为

(3)

其中,q=2,3,4,….

设随机Dirichlet级数

(4)

令

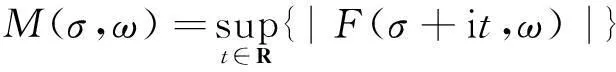
表示F(s,ω)的最大模,其中{Xn(ω)}是概率空间(Ω,A,P)中独立、一致非退化随机变量序列,且不一定是同分布的序列,且满足下列条件:E{Xn(ω)}=0,

(5)

(6)

其中,d>0是常数.记σn为E|Xn|2,因此条件(5)和下面的条件等价

(7)

本文涉及到的值分布的记号均与文献[5,12]相同.

引理 1[8]设随机变量{Xn(ω)}是非退化,系统和非独立的复随机变量,满足条件(6)及(7)式,那么:

(i) 对任何Ω∈ω,a.s.,存在N(ω)∈N,

(ii) 对{Xn}的任何子列{Xnk},

其中,d和σnk满足条件(6);

(iii) 存在β∈(0,1)使得

引理 2[9]设Dirichlet级数(1)是满足条件(2)的整函数,其中ρ由(3)式定义,则有

(8)

其中q=2,3,….

定理 1设由(4)式定义的随机Dirichlet级数

满足引理1的条件及

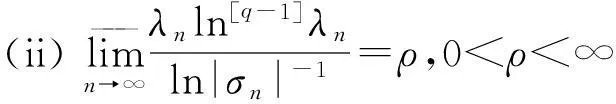
那么F(s,ω)a.s.是ρ级整函数,且a.s.每条水平直线{s:Ims=t0(t0∈R)}是F(s,ω)的没有有限例外值的q-级Borel线,即∀t0∈R,a∈C,η>0有

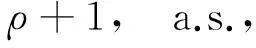
(9)

其中

为了证明定理,需要给出一些引理.

引理 3[5]设{Xn(ω)}是概率空间(Ω,A,P)中的复随机变量列,它们的数学期望E(Xn(ω))=0,且方差

(10)

则对任意H∈Λ,P(H)>0,存在正数B=B(d,H),K=K(H,{Xn})∈N,使得对任何复数列{bn}∈C,及任何自然数p与q,p>q≥K恒有

(11)

引理 4设由(4)式定义的随机Dirichlet级数

满足引理3的条件及

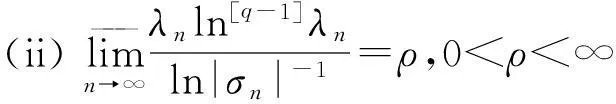
则∀t∈R有

证明由(3)式知随机Dirichlet级数的级为

令

故有m0和n0使P(H′)>0,其中

记

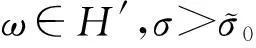
(12)

由引理3,存在自然数N=N(H′,{Xn}),正数B=B(d,H′)使得

由(12)式

所以

其中C为一正常数.

因此对任意n有

于是

令

则有

于是

与条件(ii)矛盾.故引理4得证.

系在引理4的条件下,∃E∈λ,P(E)=1,∀ω∈E,及任何实数β<γ有

仿照引理4可以证明.

为了讨论由(4)式所表示的随机整函数F(s,w)的值分布问题,需要将带形上的解析函数转化为单位圆盘上的解析函数.

引理 5[5]设{Xn(ω)}是满足引理1的随机变量,设它及函数列

定义{z:|argz-θ|

eiθa.s.是gω(z)的一个ρ(ρ>1)级Borel点,那么eiθa.s.是gω(z)的没有有穷例外值的Borel点.

由引理4的系知,∃E∈A,P(E)=1,对∀ω∈E,t0∈R,η>0有

(13)

考虑单射

和

(14)

记其逆映射为s=φ1(z)和z=φ2(W),

令

那么

(15)

和

(16)

引理 7[5]设函数f(z)、f1(z)、f2(z)在单位圆内亚纯、两两互异,并且

那么对于任意给定的常数m>0,

其中,A是绝对常数,B是赖于函数f(z)、f1(z)、f2(z)的常数.

在引理4的条件下,由映射(14)把级数

变成D(1)上随机级数

(17)

引理 8关于在D(1)内的级数ψ(W,ω)有

(18)

表明ψ级为ρa.s.,并且对所有a∈C有

(19)

从而

其中

R0是(0,1)中一个固定的数.引理8根据文献[10]的引理4可以证明.

2定理1的证明

证明(i) 首先证明F(s,ω)a.s.是整函数,根据引理1的(i)及(ii)容易证得.

(ii) 其次证明(9)式成立.由引理4及系,得(13)式成立.又由

结合(15)及(16)式有

故(18)式成立,即

由Navalinna第二定律

对任何a∈C(至多有一个例外)成立.由引理8知

那么

(20)

是D(1))上q-级为ρ的解析函数.

(21)

其中

令E∞={c:c∈C∞},记

记(c,B,μn)为Xn(ω)产生的概率空间,令

由引理1得

故P(S)=0,这就证明了对所有的a∈C,(19)式成立.又

其中

因此由上式及引理8可得(9)式成立.

致谢楚雄师范学院校级科研项目(2012)对本文给予了资助,谨致谢意.

参考文献

[1] MANDELBROJT S. Series Adherentes Regularisation des Suites Application[M]. Paris:Gauthier-Villars,1952.

[2] VALIRON G. Entire function and Borel’s directions[J]. Proc Nat Acad Sci,1934,20:211-215.

[3] PALEY R E A C, ZYGMUND A. On some series of functions[J]. Proc Cambridge Phil Soc,1930,26:337-357.

[4] LITTLEWOOD J E, OFFORD A C. On the distribution of zeros and a values of a random integral function[J]. Ann Math,1948,49:885-952.

[5] 余家荣,丁晓庆,田范基. Dirichlet级数与随机Dirichlet级数的值分布[M]. 武汉:武汉大学出版社,2004:134-146.

[6] YU J R. Julia lines of random Dirichlet series[J]. Bull Sci Math,2004,128:341-353.

[7] YU J R. Borel lines of random Dirichlet series[J]. Acta Math Scientia,2002,B22:1-8.

[8] JIN Q Y, SUN D Ch. Julia lines of general randaom dirichlet[J]. Czechoslovak Math J,2012,137(62):919-936.

[9] 孔荫莹. Dirichlet-Hadamard乘积的q-级和q-型[J]. 数学学报,2009,52(6):1165-1172.

[10] KONG Y Y. Borel radius andT-radius of the Algebroidal function in the unit disk[J]. Acta Math Sinica,2012,B32(5):1805-1812.

[11] KONG Y Y, GAN H l. On orders and types of Dirichlet series of slow growth[J]. Turk J Math,2010,34:1-11.

[12] 杨乐. 值分布理论及其新研究[M]. 北京:科学出版社,1982:7-31.

[13] 郑建华. 亚纯函数值分布理论[M]. 北京:清华大学出版社,2011:163-180.

[14] 孔荫莹,霍颖莹. 慢增长的随机Dirichlet 级数[J]. 数学年刊,2012,A33(3):323-328.

[15] HUO Y Y, KONG Y Y. On filling discs in the strong Borel direction of algebroid function with finite order[J]. Bull Korean Math Soc,2010,47(6):1213-1224.

[16] 金其余,孙道椿. 全平面上的随机Dirichlet级数的值分布[J]. 数学物理学报,2009,A29(4):1044-1050.

[17] 张洪申,孙道椿. 右半平面上Laplace-Stieltjes变换的Picard点[J]. 四川师范大学学报(自然科学版),2013,36(2):226-228.

[18] 谭洋. 全平面内随机 Dirichlet 级数的几个定理[J]. 纯碎数学与应用数学2014,30(15):512-519.

[19] 张毅,熊维玲. 关于f- [f′]的值分布[J]. 西南大学学报(自然科学版),2009,34(6):1-5.

2010 MSC：30B50

(编辑李德华)

Borel Lines of the Random Dirichlet Series ofq-order on the Whole Plane

LI Yunxia

(SchoolofMathematicsandStatistics,ChuxiongNormalCollege,Chuxiong67500,Yunnan)

Abstract：In this paper, the value distribution of the random entire function F(s,ω) defined by some random Dirichlet series of q-order on the whole plane is obtained. It is proved that, for some random Dirichlet series of q-order, almost surely every horizontal line is a Borel line of q-order without finite exceptional values.

Key words：random Dirichlet series; q-order; Borel line

doi:10.3969/j.issn.1001-8395.2016.01.017

中图分类号：O174.52

文献标志码：A

文章编号：1001-8395(2016)01-0098-05

作者简介：李云霞(1970—),女,教授,主要从事复分析的研究,E-mail:cxliyunx@126.com

基金项目：云南省应用基础研究面上项目(2007A229M)

收稿日期:2014-09-07