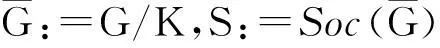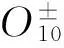次数分别为81和82的对称群的OD-刻画
余大鹏, 晏燕雄, 李金宝, 张良才
( 1. 重庆文理学院 数学与财经学院, 重庆 402160; 2. 西南大学 数学与统计学院, 重庆 400715;
3. 重庆大学 数学与统计学院, 重庆 401331)
次数分别为81和82的对称群的OD-刻画
余大鹏1,晏燕雄2,李金宝1,张良才3
(1. 重庆文理学院 数学与财经学院, 重庆 402160;2. 西南大学 数学与统计学院, 重庆 400715;
3. 重庆大学 数学与统计学院, 重庆 401331)
摘要:利用群的阶和群的素图度数序列分别刻画次数为81和82的对称群,证明对称群S(81)和S(82)均可3-重OD-刻画的.值得指出的是,该结论对文献(Y. X. Yan, G. Y. Chen, L. C. Zhang, et al. Chinese Annals Math.,2013,34:777-790.)中提出的公开问题给予肯定的回答.
关键词:素图; 单群; 顶点的次数; 素图度数序列; 对称群
1预备知识及主要结果
设G是有限群,用πe(G)表示群G中元素所有阶的集合;用π(G)表示群G的阶的全体互异素因子之集;与群G有关的Gruenberg-Kegel图记为Γ(G),其中,Γ(G)的顶点集为π(G),Γ(G)中两不同顶点r、s相连当且仅当rs∈πe(G),并记为r~s[1-2];用π(n)表正整数n中所有互异素因子的集合;用Soc(G)表示群G的基柱,它由群G的所有极小正规子群组成;用Sylp(G)表示群G的所有Sylowp-子群的集合,其中,p∈π(G);用Pr表示群G的Sylowr-子群,其中,r∈π(G);用An和Sn分别表示次数为n的交错群和对称群.其它未说明的符号见文献[3].

定义 1.2[4]群M称为可k-重OD-刻画,如果恰好存在k个不同构的群G使得|G|=|M|且D(G)=D(M).特别地,称可1-重OD-刻画群为可OD-刻画的.
文献[1,4-14]等中证明了许多(几乎)单群都是可n-重OD-刻画的,其中n≥1.
命题 1.1设p为素数,如果G同构于下述群之一,则群G是可OD-刻画的.
1) 除Aut(J2)和Aut(McL)之外的散在单群的自同构群;
2) 对称群Sp、Sp+1及交错群Ap、Ap+1、Ap+2;
3) 除A10以外的所有K4-单群;
4) 李型单群L2(r)、U3(r)、L3(r)、2B2(r)及2G2(r),其中r为某素数的方幂;
5) 所有C2,2-群;
6) 交错群Ap+3,这里7≠p∈π(100!);
7) 除Aut(A6)和Aut(U4(2))外的K3-单群的自同构群.
命题 1.2设p为素数,如果G同构于下述群之一,则群G是可3-重OD-刻画的.
1) 对称群Sn,其中,n≠p,p+1且10 2) 对称群Sp+3,其中,101 命题 1.3有限群G满足|G|=|S10|且D(G)=D(S10),则G是可8-重OD-刻画的. 由上所述,对称群Sp和Sp+1是可OD-刻画的;当n≠p,p+1且10 公开问题[1]除S10外,是否所有对称群Sn(n≠p,p+1)都是可3-重OD-刻画的? 对于素数p,由于Sp和Sp+1是可OD-刻画的,现不考虑这些系列的可OD-刻画的对称群,则剩下对称群群列如下: 容易看到对称群列(*)中的每个群的素图都是连通的.对称群S10为8-重OD-刻画群(见命题1.3),而S10是第一个被证明不是可OD-刻画的对称群.命题1.2的研究表明了许多对称群也不是OD-刻画的.因此究竟有多少对称群不是可OD-刻画的,还没有人能给出正面的回答.本文将继续这一问题的研究,并就对称群S81和S82对文献[1]中的猜想作出肯定的回答,主要结果如下. 定理 1.1设有限群G满足|G|=|S81|且D(G)=D(S81),则G同构于下列群之一:S81,Z2·A81或Z2×A81,即S81是可3-重OD-刻画的. 定理 1.2设有限群G满足|G|=|S82|且D(G)=D(S82),则G同构于下列群之一:S82,Z2·A82或Z2×A82,即S82是可3-重OD-刻画的. 2主要引理 引理 2.2[3,16]令F79为最大素因子不超过79的有限非交换单群全体所成之集.若S∈F79,则S同构于表1所述的群之一.特别地,若|π(Out(S))|≠1,则π(Out(S))⊆{2,3,5}. 引理 2.3[17]设S=S1×S2×…×Sk,其中,Si(i=1,2,…,k)是ni个同构非交换的单群Hi的直积且如果i≠j,有HiHj,则有 Aut(S)=Aut(S1)×Aut(S2)×…×Aut(Sk) 且Aut(Si)=Aut(Hi)Sni,其中,Sni是ni次对称群.进一步 Out(S)=Out(S1)×Out(S2)×…×Out(Sk) 且Out(Si)=Out(Hi)Sni. 3定理的证明 下面分别证明定理1.1和1.2. 定理1.1的证明设有限群G同时满足: 1) |G|=|S81|=278·340·519·712·117·136·174·194·233·292·312·372·41·43·47·53·59·61·67·71·73·79和D(G)=D(S81)=(21,20,20,20,18,18,17,17,15,14,14,13,12,12,11,9,8,8,6,4,4,1).由假设和引理2.1知有{p}∪{pq|p+q≤81}⊆πe(G)和{pq|p+q>81}∩πe(G)=Ø成立,其中,p,q∈π(G).由于deg(2)=21且|π(G)|=22,故G的素图是连通的.应用计算群论软件Magma并根据D(G)的结构进行简单验算,可知Γ(G)=Γ(S81). 下面将定理的证明分解为3个主要引理来证明. 引理 3.1若K是群G的极大可解的正规子群,则K是{2,3}-群.特别地,G不可解. 证明首先断言K是79′-群.否则,群K必包含79阶元素,不妨设为x.因为deg(79)=1以及2+79≤81,由引理2.1知CG(x)是{2,79}-群.由N/C定理有 因此,NG(x)是{2,3,13,79}-群.由Frattini论断,有G=KNG(x),因而有{5,11,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79}⊆π(K).因为K是可解群,故K中存在71·73阶Hall{71,73}-子群L.显然,L是交换的,故71·73∈πe(G).又由引理2.1有71+73>81,知71·73∉πe(G),矛盾.故断言成立. 下面证明K是p′-群,这里的素数p∈{5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79}.设p∈π(K)并且p∈Sylp(K).又由Frattini论断可得G=KNG(P),因此79||NG(P)|.现设T是NG(P)的79阶子群.因T正规化P,应用Magma软件简单的计算知:当素数p≠23时,79⫮|Aut(P)|;故对于每个素数p且p≠23,有79p∈πe(G).但是由引理2.1知79+p>81,因此79p∉πe(G),矛盾.如果p=23且79||Aut(P)|,通过简单的验算,此时有 表 1 有限非交换单群S且π(S)⊆{2,3,5,7,…,79} 若73||NG(P)|,则73∈π(CG(P)).从而23·73∈πe(G),这矛盾于引理2.1.因此73∈πe(K).因为K是可解,从而K中存在23i·73阶Hall{23,73}-子群,其中,i=1,2或3.因为73⫮Aut(Syl23(K)),故23·73∈πe(G),这矛盾于引理2.1.综上,证明了K是{2,3}-群.因为K≠G,所以G是不可解的. 引理 3.2设K是群G的极大可解的正规子群,则商群G/K是几乎单群,即存在有限非交换单群S使得SG/KAut(S). 因此m=1,即S=B1∈F79.由N/C定理有 引理 3.3G≅S81,Z2·A81或Z2×A81,即S81是可3-重OD-刻画的对称群. 证明根据引理3.1和引理3.2,不妨假设|S|=|S81|=2a·3b·519·712·117·136·174·194·233·292·312·372·41·43·47·53·59·61·67·71·73·79,其中,2≤a≤78,1≤b≤40.根据表1,则知S只可能同构于下列群之一:A79、A80、A81或A82. 由引理2.2及|G|3=40,通过比较这些群的阶,则SA79或A80.再由|G|41=1知,SA82.因此只能是S≅A81.此时,A81G/KAut(A81)≅S81. 若G/K≅S81,比较阶可知K=1且G≅S81. 若G/K≅A81,此时|K|=2,因此K≤Z(G)∩G′.故G是Z2被A81的中心扩张,且G同构于2·A81(Z2被A81的非可裂中心扩张)或者2:A81≅Z2×A81(Z2被A81可裂的中心扩张).进一步,无论G同构于2·A81还是2:A81,由文献[3]简单的验算知有限群2·A81和2:A81均满足条件|G|=|S81|和D(G)=D(S81).因此,S81是可3-重OD-刻画的. 定理1.2的证明设有限群G满足|G|=|S82|=279·340·519·712·117·136·174·194·233·292·312·372·412·43·47·53·59·61·67·71·73·79和D(G)=D(S82)=(21,21,20,20,19,18,17,17,16,15,14,13,12,12,11,10,9,8,6,5,4,2).由假设和引理2.1,可得到{p}∪{pq|p+q≤82}⊆πe(G)和{pq|p+q>82}∩πe(G)=Ø,其中,p,q∈π(G).因为顶点3的次数deg(3)=21=|π(G)|-1,故群G的素图是连通的.再次根据D(G)的结构及计算群论软件Magma的验算,可知Γ(G)=Γ(S82). 令K是群G的极大的可解的正规子群,用完全类似于引理3.1的证明方法,可证K是{2,3}-群,且有A82G/KAut(A82)≅S82.如果G/K≅S82,比较阶得K=1且G≅S82.如果G/K≅A82.此时|K|=2,故K≤Z(G).从而G是Z2被A82的中心扩张.并且G同构于下述群之一:2·A82(Z2被A82的非可裂中心扩张);2:A82≅Z2×A82(Z2被A82可裂的中心扩张).由于定理1.2的证明方法完全类似于定理1.1,因此略去了详细的证明过程.故S82是可3-重OD-刻画的对称群. 参考文献 [1] YAN Y X, CHEN G Y, ZHANG L C, et al. Recognizing finite groups through order and degree pattern[J]. Chinese Annal Math,2013,34:777-790. [2] WILLAMS J S. Prime graph components of finite groups[J]. J Algebra,1981,69(2):487-513. [3] CONWAY J H, CURTIS R T, NORTON S P, et al. Atlas of Finite Groups[M]. London,New York:Clarendon Press,1985. [4] MOGHADDAMFAR A R, ZOKAYI A R, DARAFSHEH M R. A characterization of finite simple groups by the degrees of vertices of their prime graphs[J]. Algebra Colloquium,2005,12(3):431-442. [5] MOGHADDAMFAR A R, ZOKAYI A R. OD-characterization of alternating and symmetric groups of degrees 16 and 22[J]. Frontiers of Mathematics in China,2009,4(4):669-680. [6] HOSEINI A A, MOGHADDAMFAR A R. Recognizing alternating groupsAp+3for certain primespby their orders and degree patterns[J]. Frontiers of Mathematics in China,2010,5(3):541-553. [7] ZHANG L C, SHI W J. OD-characterization of simpleK4-groups[J]. Algebra Colloquium,2009,16(2):275-282. [8] YAN Y X, CHEN G Y, XU H J. A new characterization of certain symmetric and alternating groups[J]. Adv Math,2013,42(5):601-610. [9] YAN Y X, XU H J, CHEN G Y, et al. OD-characterization of the automorphism groups of simpleK3-groups[J]. J Ineq Appl,2013,2013:1-13. [11] YAN Y X. OD-characterization of the symmetric groupS28[J]. Adv Mater Research,2011,396-398:140-143. [12] YAN Y X, CHEN G Y. OD-characterization of alternating and symmetric groups of degree 106 and 112[J]. Proc Inter Conf Algebra,2010,2011:690-696. [13] 晏燕雄. 与Chevalley群F4(2)有关的几乎单群的OD-刻画[J]. 西南大学学报(自然科学版),2011,33(5):112-115. [14] 余大鹏,李金宝,张良才,等. Lie型单群D6(2)和D6(3)的OD-刻画[J]. 西南师范大学学报(自然科学版),2014,39(12):1-5. [15] ZAVARNITSINE A, MAZUROV V D. Element orders in covering of symmetric and alternating groups[J]. Algrbra and Logic,1999,38(3):159-170. [16] ZAVARNITSINE A V. Finite simple groups with narrow prime spectrum[J]. Siberian Electronic Math Reports,2009,6:1-12. [17] ROBINSON D J S. A Course in the Theory of Groups[M]. New York:Springer-Verlag,2001. 2010 MSC:20B30 (编辑李德华) OD-Characterization of Symmetric Groups of Degree 81 and 82 YU Dapeng1,YAN Yanxiong2,ZHANG Liangcai3,LI Jinbao1 (1.DepartmentofMathematicsandFinance,ChongqingUniversityofArtsandSciences,Chongqing402160;2.SchoolofMathematicsandStatistics,SouthwestUniversity,Chongqing400715;3.SchoolofMathematicsandStatistics,ChongqingUniversity,Chongqing401331) Abstract:In this paper, it is proved that the symmetric groups S(81) and S(82) can be characterized by their orders and degree patterns. In fact, the symmetric groups S(81) and S(82) are 3-fold OD-characterizable. This result gives a positive answer to an open problem in (Y. X. Yan, G. Y. Chen, L. C. Zhang, et al. Chinese Annals Math.,2013,34:777-790.) Key words:prime graph; simple group; degree of a vertex; degree pattern; symmetric group doi:10.3969/j.issn.1001-8395.2016.01.015 中图分类号:O152.1 文献标志码:A 文章编号:1001-8395(2016)01-0088-05 作者简介:余大鹏(1971—),男,副教授,主要从事代数学群论的研究,E-mail:yudapeng0@sina.com 基金项目:国家自然科学基金(11171364、11271301和11471266)、国家自然科学基金数学天元基金(11426053)、中国博士后科学基金(2014M562264)、重庆市博士后科学基金(XM2014029)、中央高校基本业务费专项基金(XDJK2014C162)、重庆市自然科学基金(CSTC2015JCYJA00052、CSTC2013JCYJA00034和CSTC2014JCYJA00010)和重庆市教委自然科学基金(KJ131204) 收稿日期:2014-04-28