含辅助信息的最小非参似然比估计和检验

侯瑞环,　王　沁,　李裕奇

(1. 塔里木大学 信息工程学院, 新疆 阿拉尔 843300;　2. 西南交通大学 数学学院, 四川 成都 610031)



含辅助信息的最小非参似然比估计和检验

侯瑞环1,2,王沁2,李裕奇2

(1. 塔里木大学 信息工程学院, 新疆 阿拉尔 843300;2. 西南交通大学 数学学院, 四川 成都 610031)

摘要：当前,拟合优度检验已经比较完善,但仍存在对总体分布已有信息利用不足或者直接丢掉这部分信息的问题.为了实现对已有信息的充分利用,首先借助经验似然的思想与最小非参似然比统计量的形式,给出含辅助信息的最小非参似然比统计量;然后利用最小非参似然比估计与检验性质的研究方法,得到含辅助信息的最小非参似然比估计量,并考察检验统计量的相合性、稳健性,同时得到其在复合零假设下的极限分布.这些结论在一定程度上可以丰富和完善拟合优度检验与非参数估计的一些理论.

关键词：经验似然; 辅助信息; 非参数似然比; 经验分布

在实际数据处理过程中,通常所抽取的样本都是来自未知总体,然后再根据所得数据对总体做出推断.这里面主要有2个问题:估计和推断.从已知分布入手解决这一问题,是统计学界长期关注与研究的课题之一.然而,要解决这类问题的关键要知道这组数据的分布或者分布族,也就是统计中的拟合优度检验问题.对于来自未知总体F的独立同分布样本X1,…,Xn,拟合优度检验一般考虑如下2种问题的检验:

(1)

(2)

其中,F0是已知的分布函数,Fθ={Fθ:θ∈Θ}是一个含有未知参数的分布族.

对(1)式的检验,当属KarlPearson在1900年提出的χ2检验,经过多年的发展,χ2型检验理论已经相当之完善,又因计算简单,时至今日,χ2型检验[1-2]仍然是统计应用中较为广泛的检验之一.但是,χ2型检验却有着“先天”的不足之处,为了弥补这一不足,人们提出了基于经验分布(EDF)的检验,EDF型检验主要有20世纪20—30年代提出的CV和KS统计量.到20世纪50年代,Anderson和Darling提出AD统计量及加权CV和KS统计量;20世纪70年代末,由R.H.Berk等[3]提出了似然比统计量;进入21世纪以来,又先后有了EM统计量和修正的BJn统计量BWn.随后,文献[4-7]分别从不同研究角度给出了上界型统计量和积分型统计量.对问题(2)的研究主要集中于2种途径:一是先对未知参数做出相应估计,再利用已有的检验方法做检验;另一种则是对一些特殊分布,利用充分统计量,给出条件积分变换,由于对分布有一定的要求,以至于在实际应用中不具有普遍性.由前述发现,不论哪种方法,除了检验统计量本身好坏之外,参数估计好坏直接影响着检验的好坏,经典的参数估计有极大似然估计和最小距离估计,由于常见分布的参数极大似然估计计算容易,故其应用相当广泛;最小距离估计在上世纪得到了相应的研究,因为其计算较为繁琐,所得估计收敛速度较慢,但应用并不广泛,直到进入20世纪,最小距离估计又得到了重视.然而这些统计量都无法更好地满足人们的研究需求,所以近些年又出现了非参数似然比拟合优度检验统计量及最小非参数似然比拟合优度检验统计量.在实际应用中抽取样本时往往会得到一些关于总体分布的辅助信息,为了能够将这些信息加以有效利用,本文利用这2种统计量研究的思想与方法,给出含辅助信息的最小非参数似然比统计量,并从理论上对其估计和检验的相关性质及统计量的极限分布进行研究,得到相应结果.

1预备知识

1.1统计量提出

定义 1.1设X1,X2,…,Xn是来自于未知总体F的独立同分布样本,假设已有一些与总体相关的辅助信息,也就是存在r(r≥1)个函数g1(x),g2(x),…,gr(x)使得

EFg(X)=0,

这里g(X)=(g1(x),g2(x),…,gr(x))T.上述以定义的方式给出辅助信息,具体与辅助信息有关内容见文献[8-10].

定义 1.2假设G为任意分布函数,对应的上界型非参似然比统计量为

(3)

(4)

当G=Fn时,T(G)就是最小非参似然比估计;

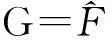
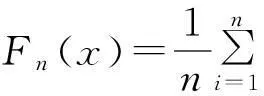
1.2存在性证明

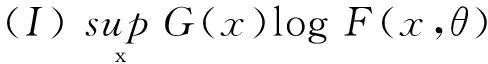
则BJG(θ)关于θ∈Θ1连续,且满足(4)式的T(G)所组成的集合为紧致的非空子集.

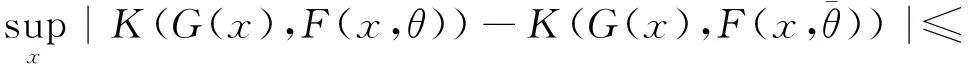
由条件(I)和(II)可知结论成立.

2含辅助信息最小非参统计量性质研究

统计量估计的相合性:

可知,当n→∞时有

当且仅当不含辅助信息,即g(Xi)=0时等号成立,

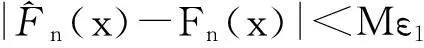
定理 2.1假设T(G)的值唯一,对于任意θ∈Θ1有

统计量估计[14]的稳健性:

定理 2.2假定对任一x∈R,F(x,θ)关于θ的二阶导数存在且连续,BJG(θ)关于θ的某个领域内二阶可微,并且二阶偏导数矩阵连续可逆,则在T(G)处的响应函数为

(5)

其中,θ=T(G)∈Θ1,Δx为在x退化分布,P(G)为BJG(θ)在θ处的二阶偏导数矩阵,即

含有辅助信息最小非参似然比检验统计量的极限分布:

引理 2.2假设对θ0的每一个邻域Ω,存在某一正常数C,使得当θ∉Ω时,对任意正δ有

成立,且对θ0的每一个邻域Ω,当n→∞时有

(6)

从而当n→∞时有

(7)

所以有

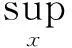
定理 2.3假设F(x,θ)在θ0处可微,且存在一个常数C,使得任意θ∈Rm(m为参数的维数)有

且

则在引理2.2条件下有

与

有相同的极限分布.由此可知含有辅助信息最小非参似然比检验统计量的极限分布存在,可以按两部分理解:第一部分由于含辅助信息经验似然分布函数所导致的极限分布;另一部分为参数估计所引起的偏差部分.

3结语

至此,估计量T(G)的解是存在的,并且含辅助信息的最小非参似然比估计弱相合.另外影响估计稳健性的因素是AG(△x):当|AG(△x)|有界时,估计是稳健的;当|AG(△x)|无界时,一般得不到稳健估计.这里的AG(△x)与分布函数有关,因此要想得到稳健的估计,则必须考虑分布族.并从理论上证明了含辅助信息的非参似然比检验的极限分布是存在的,并且其与含辅助信息经验似然分布函数和参数估计所引起偏差两部分有关.

定理2.1证明由含辅助信息的最小非参似然比估计

在此处,首先得说明

然而

由文献[15]定理2.15容易得到

再结合定理条件2.1与引理2.1知

这与T(G)的唯一性相互矛盾,因此所有子序列均依概率收敛到.

定理2.2证明因为

所以

其中▽BJG(θ)表示BJG关于θ的一阶偏导向量.

假设对于任意ε>0,Gε(t)=(1-ε)G(t)+ε△x(t),故而

综上可以得到

又因为

其中θ1介于T(Gε)与T(G)之间.

其中,▽2BJG(θ)表示BJG关于θ的二阶偏导矩阵,从而T在G处的影响函数为

定理2.3证明因为

对logF(x,θ)在F(x,θ0)处Taylor展开

类似的也可以对log(1-F(x,θ))在F(x,θ0)展开

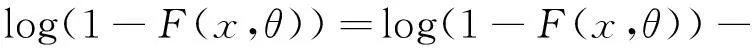
所以将上述2式代入下式有

又因为有

所以

故而由定理2.3的条件与引理2.2及类似于文献[16]的结论得到结果.

参考文献

[1] 陈希孺,方兆本,李国英,等. 非参数统计[M]. 合肥:中国科学技术大学出版社,2012.

[2] 李裕奇,赵联文,王沁,等. 非参数统计方法[M]. 成都:西南交通大学出版社,2010.

[3] BERK R H, JONES D H. Goodness-of-fit statistics that dominate the Kolmogorov statistics[J]. Z Wahrsch-Verw Gebiete,1979,47:47-59.

[4] ZHANG J. Power full goodness-of-fit tests on the likelihood ratio[J]. J Royal Statistical Society Soc,2002,B64(2):281-294.

[5] 张军舰,杨振海,程维虎. 拟合优度检验[M]. 北京:科学出版社,2010.

[6] 张军舰,李国英. 上界型拟合优度检验[J]. 数学物理学报,2010(2):344-357.

[7] JAGER L, WELLNER J A. A New Goodness of Fit Test:the Reversed Berk-Jones Statistic[M]. Seattle:University of Washington,2004:1-21.

[8] ZHANG B. M-estimation and quantile estimation in the presence of auxiliary information[J]. J Statistical Planning and Inference,1995,44:77-94.

[9] ZHANG B. Confidence intervals for a distribution function in the presence of auxiliary information [J]. Comput Statistics Data Analysis,1996,21:327-342.

[10] FENG L X, LI R. Smoothed empirical likelihood confidence intervals for quantile regression parameters with auxiliary information[J]. Statistical Methodology,2013,15:46-54.

[11] OWEN A B. Empirical likelihood ratio confidence intervals for a single function[J]. Biometrika,1988,75(2):237-249.

[12] OWEN A B. Non parametric Likelihood Confidence Bands for a Distribution Function[J]. J Am Statistical Association,1995,90:516-521.

[13] 林正炎,陆传荣,苏中根. 概率极限理论基础[M]. 北京:高等教育出版社,1999.

[14] 许宝,姜玉秋,藤飞. 一种加权对称损失函数下一类指数分布模型参数的估计[J]. 四川师范大学学报(自然科学版),2011,34(4):484-487.

[15] 张军舰. 广义非参似然比拟合优度检验[D]. 北京:中国科学院,2006.

[16] POLLARD D. The minimum distance method of testing[J]. Metrikea,1980,27:43-70.

2010 MSC：62G86

(编辑郑月蓉)

Minimum Non-Parametric Likelihood Ratio Estimation and Testing in the Presence of Auxiliary Information

HOU Ruihuan1,2,WANG Qin2,LI Yuqi2

(1.CollegeInformationEngineering,TarimUniversity,Alar843300,Xinjiang;2.SchoolofMathematics,SouthwestJiaotongUniversity,Chengdu610031,Sichuan)

Abstract：Currently, though the goodness of fit test is already fairly complete, there are still existing some outstanding problems, which will be lack of existing information or losing partly information directly during estimating the distribution. In order to achieve full utilization of existing information, first of all, with the idea of empirical likelihood and the form of minimum non-parametric likelihood ratio statistic, the paper gives the minimum nonparametric likelihood ratio statistic with the presence of auxiliary information. Then, using a minimum non-parametric likelihood ratio estimation and testing methods, the minimum nonparametric likelihood ratio estimator with the presence of auxiliary information is obtained. At last, the feature of consistency and robustness are studied, at the same time, the limit distribution in composite null hypothesis is got. To some extent, these conclusions can enrich and improve the theories of goodness testing and the nonparametric estimation.

Key words：empirical likelihood; auxiliary information; nonparametric likelihood ratio; empirical distribution

doi:10.3969/j.issn.1001-8395.2016.01.010

中图分类号：O212.7

文献标志码：A

文章编号：1001-8395(2016)01-0059-06

*通信作者简介：王沁(1973—),女,副教授,主要从事应用、经济统计、管理科学与工程的研究,E-mail:wangqin@home.swjtu.edu.cn

基金项目：中央高校基本科研业务费专项资金(SWJTU11CX155)

收稿日期:2014-03-24