基于强化学习和蚁群算法的协同依赖多任务网格集群调度

张新华

(太原学院计算机系,山西 太原 030012)



基于强化学习和蚁群算法的协同依赖多任务网格集群调度

张新华

(太原学院计算机系,山西 太原 030012)

摘要：针对现有的网格集群资源调度方法所具有的任务调度时间长、系统负载不均衡和CPU利用率低的缺点，提出了一种基于强化学习和蚁群算法结合的协同依赖型任务调度方法.首先对调度目标模型进行了定义，然后采用改进的强化学习Sarsa算法实现集群资源的初始分配，以最小化任务调度时间为目标，寻求最优调度方案，并保存调度方案对应的Q值.在此基础上，设计了一种改进的蚁群算法实现网格集群资源到任务分配的进一步寻优，在不同资源节点上的概率选择上考虑了Q值因素，从而实现网格环境下的协同依赖多任务集群调度.在Gridsim工具下进行仿真试验，结果表明新方法能有效地实现协同依赖多任务网格集群调度，且较其他方法而言，具有任务调度时间少、CPU利用率高和负载均衡的优点，是一种适合网格环境的可行任务调度方法.

关键词：集群调度；资源分配；蚁群算法；强化学习

网格计算[1]是将各类资源连接而形成的共享资源系统，能整合网络异构资源，实现动态和多制度的虚拟组织的资源共享，并采用共享资源协同工作的形式为用户提供服务[2,3].

网络资源任务分配是网格计算研究的重点课题，主要是致力于实现在满足用户需求的前提下，将网格任务分配到合适的计算资源上，使得任务的执行能尽可能快且资源利用率能足够高[4,5].

网格任务资源调度已被证明是一个NP难题，经典的网格调度方法主要是：Min-min方法[6]和Max-min方法[7].

相比Min-min方法，Max-min方法的优势在于：每次选择具有最大最小完成时间的任务进行调度，能较大程度地改善网络负载均衡和提高资源利用率.

为了克服Max-min方法和Min-min方法的不足，文献[8]设计了一种基于小生境和遗传算法的网格任务调度，首先描述了依赖型任务调度DAG模型，然后采用小生境预选择机制对种群个体进行选择，从而提高算法的全局寻优能力.文献[9]设计了一个单层树型网格周期性调度方法，为网格独立任务建立线性规划模型，然后通过整数线性规划求解，将大规模的任务调度问题转换为一个周期内的任务调度.文献[10]设计了一种融合配方均匀设计与离散粒子群算法的任务调度策略，实现独立任务优化调度，产生分布均匀且较优的Pareto解集.

上述工作在一定程度上克服了Max-min算法和Min-min算法的不足，具有重要的意义，但仍然存在着无法在线实时分配和分配效率不高的问题，为此，文中设计了基于强化学习和蚁群算法结合的任务在线分配算法，并通过实验证明了其有效性.

1网格依赖任务模型

依赖型网格任务调度系统可以表示为一个六元组DAG={T,E}，T={t1,t2,…,tn}表示n个任务组成的任务集合，E={(ti,tj)}1≤i,j≤n表示任务依赖集，表明任务tj在ti执行完成后才能执行，无任何前驱的任务叫入口任务，无任何后继任务的任务叫做出口任务.每个任务ti对应的指令数为ci，每条边的数据传输量表示为dij，对于整个任务集都有一个入口任务tin和一个出口任务tout.

当任务集无统一的入口任务时，可以建立一个虚拟的入口任务，并将其指向所有入度为0的节点.

当任务集无统一的出口任务时，可以建立一个虚拟的出口任务，并将出度为0的节点都指向虚拟的出口任务.

一个依赖型有向无环图DAG可以表示为如图1所示：

图1　依赖型任务对应的DAG

定义1 任务执行时间：对于给定的任务ti∈T，其分配到某节点PEj上的运行时间为PE(ti)，可以通过下式计算：

(1)

其中，mi为任务ti的计算量，spe(j)为节点PEj的处理速度.

定义2 数据传输时间：采用ti j表示任务ti和tj的数据传输时间，当两个任务分配在同一个处理节点上时，传输时间为0，否则为数据传输量与两个处理节点通信带宽的比值，如下所示：

其他

(2)

定义3 任务入口路径：对于任意任务ti∈T，其任务入口路径为入口任务tin到达当前任务ti的最长路径长度，即为In_pathi，可以通过下式计算：

(3)

定义4 任务出口路径：对于任意任务ti∈T，其任务出口路径为当前任务ti到出口任务tout的最长路径长度，即为Out_pathi，可以通过下式计算：

(4)

定义5 最早开始时间：对于任意任务ti∈T，其最早开始时间是指其所有前驱任务的最早完成时间或其所分配的节点的最早空闲时间，记为starti(ti,PE(ti))：

starti(ti,PE(ti))=max{startj+tij+ti,startPE+tPE}

(5)

定义6最早完成时间：对于任意任务ti∈T，其最早完成时间是指将任务ti分配到处理机PE(ti)的最早完成时间：

finishi(ti,PE(ti))=starti+ti

(6)

2基于Sarsa算法的网格资源分配

2.1Sarsa算法

Sarsa算法是一种时间差分算法，它将样本表示为四元组，即：

(7)

在式(7)中state1表示当前状态，action1表示在当前状态下采取的动作，reward表示当前状态动作下的立即回报，state2表示下一个状态，action2表示在下一个状态时根据当前策略应采取的动作.根据一个样本四元组，可以获得让任一状态动作对的Q值：

Q(x,u)=Q(x,u)+α(r+γQ(x',u')-Q(x,u))

(8)

2.2基于Sarsa算法的网格资源分配

以最大化Q值为目标，当Agent每成功完成一次任务分配时，获得立即奖赏为1，当Agent完成最后一个任务分配时，并且优于所有已有方案时，立即奖赏为100，否则为1.

算法为：

(1)初始化：任务集合X，动作集合U，状态动作空间X×U，对于∀(x,u)∈X×U，初始化Q0(x,u)=0，探索因子ε，折扣因子γ，学习率α，最大迭代次数T，最大情节数ET，每个情节中的最大步数ETS，当前状态为x；

(2)当前情节数et=1；

(3)当前步数s=0；

(4)根据ε-greedy选择动作u，得到x'和r；

(5)根据ε-greedy选择状态x'的动作u'；

(6)采用式(8)计算Q值；

(7)对探索因子ε的值进行衰减，并将下一个状态赋给当前状态x←x'，将下一个动作赋给当前动作u←u'；

(8)s=s+1，判断当前情节et是否已经到达最大步数而结束情节：

如果情节结束，则当前情节数et=et+1，并转入(4)继续执行.

否则，算法迭代次数t=t+1，判断t的值，如果当前迭代次数小于T，则转入(4)继续执行； 否则算法结束，根据学习的Q值获取最优的任务动作分配方案.

(9) t=t+1，根据情节数作判断：

如果情节数达到最大值，则算法结束，输出结果.

否则转入(4)继续开始运行.

3基于并行蚁群算法的网格资源分配

3.1传统的蚁群算法

蚁群算法由意大利学者M.Dorigo等人于1991年创立，是一种基于种群寻优的启发式优化算法，具有强大的并行分布式计算能力，目前已经先后用于旅行商TSP问题(Traveling Salesman Problem)和资源二次分配问题等.

3.2基于并行蚁群算法的集群调度

算法输入：任务队列集TaskS、集群节点集P，蚁群Ant，蚁群中的蚂蚁数量K，最大迭代次数T，任务缓存队列Que，值α和β，信息素挥发率η，调节因子μ；

算法输出：任务和资源分配的一个1*n的向量；

初始化：t=1.

步骤1：根据式(6)计算所有任务的最早完成时间，根据最早完成时间对所有任务排序，并按照从早到晚的顺序依次加入等待队列Que.

步骤2：K只蚂蚁从任务等待队列Que中选取个K个任务，如果Que中的任务数量小于K，则派出与队列中任务数相同的蚂蚁数.

步骤3：根据式(9)对t+1时刻集群中资源节点进行信息素τij(t+1)更新.

τij(t+1)=(1-ρ)*τij(t)+ρΔτij(t)

(9)

在式(9)中，ρ表示信息素挥发因子和τij(t)分别表示t时刻时路径ij上的信息素.Δτij(t)为信息素的局部增量：

(10)

在式(10)中，comij为路径ij的通信时间.

步骤4：根据式(11) 选择每个蚂蚁的任务进行集群资源节点.

others

(11)

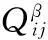
步骤5：对路径的局部信息素按公式(12)进行更新.

(12)

步骤6：判断任务等待队列是否为空，如果为空，则转入步骤7，否则保存当前K个任务的调度方案，并转入步骤2.

步骤7：t=t+1，并判断当前迭代次数t等于最大迭代次数T：

如果等于则算法结束，则输出所有任务对应的节点调度方案；否则，转入步骤2继续运行.

4实验分析

4.1实验环境和参数设置

采用GridSim进行仿真实验，集群数为3，为Cluster1、Cluster2和Cluster3，三个集群对应的初始节点数分别为8，10和13，每个节点的处理器数为4，因此，三个集群对应的资源总数分别为32、40和52，用户数分别为10、8和9，每个用户的任务数分别为2、4和2.

参数设置如下：Sarsa算法中探索因子ε=0.01，折扣因子γ=0.8，学习率α=0.1，最大迭代次数T=00，最大情节数ET=50，每个情节中的最大步数ETS=1000.

蚁群中的蚂蚁数量K=10，最大迭代次数T=50，b=0.4，信息素挥发率η=0.3，调节因子μ=0.6，权值α和β分别为0.6和 0.4，最大迭代次数设置为50次，信息素的挥发率η=0.4，调节因子μ=2.

将文中方法与文献[9]和文献[10] 进行比较，从所有任务的跨度、CPU的利用率以及负载均衡度三个方面进行比较.

4.2调度时间比较

三种方法对应的任务调度时间仿真结果如图1所示：

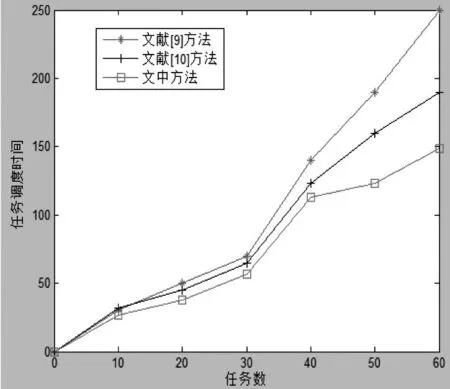
图2　任务调度时间对比

从图2中可以看出，文中在任务数从0增加到60个的过程中，文献[9]方法获得任务调度时间为104.29，文献[10]方法获得任务调度时间为87.86，文中方法得到的任务调度时间为72.43.文中方法较文献[9]方法减少了30.55%，文中方法较文献[10]方法减少了17.56%.

4.3CPU利用率

图3　CPU利用率对比

从图3中可以看出，文中方法的资源利用率在前20个任务时候基本与文献[10]方法相同，但是在20个任务后，资源利用率显著提高，较文献[9]方法提高了28.41%，较文献[10]方法提高了8.92%.

4.4负载均衡度

负载均衡离差反应了系统的负载均衡程度，其值可以通过下式计算：

(13)

从图4可以看出，文中方法的φ平均值为0.383，而文献[9]方法对应的负载均衡离差为0.590，文献[10]方法对应的负载均衡离差为0.434.

图4　负载均衡离差

5结语

针对网格复杂环境下的传统调度算法具有的任务调度时间长和CPU利用率不高的缺点，提出了一种基于强化蚁群算法的网格资源分配算法.首先采用Sarsa算法实现网格任务资源分配，然后采用并行的蚁群算法进行寻优，实现了网格任务的集群资源节点调度.通过仿真实验证明，文中方法能有效地实现任务的调度，具有CPU利用率高、调度时间短和负载均衡能力强的优点，具有较强的可行性.

参考文献：

[1]Foster I, Kesselman C, Tuecke S. The anatomy of the grid: Enabling scalable virtual organizations [J]. International J Super Computer Application, 2001,(3):200-222.

[2]马艳,龚斌,邹立达. 网格环境下基于复制的能耗有效依赖任务调度研究[J].计算机研究与发展,2013,(2):420-429.

[3]NettoMAS,BuyyaB.Reschedulingco-allocationrequestsbasedonflexibleadvancereservationsandprocessorremapping[A].Proceedingsof9thGridComputingConference[C]. 2008:144-150.

[4]王观玉．网格计算中任务调度算法的研究和改进[J].计算机工程与科学，2011，(10):186-187.

[5]LiJY，QiuMK，MingZ，etal．OnlineoptimizationforschedulingpreemptabletasksonIaaScloudsystems[J]．JournalofParallelandDistributedComputing，2012,(2):666 -677.

[6]BraunTD,SiegelHJ,BeckN.Acomparisonofelevenstaticheuristicsformappingaclassofindependenttasksontoheterogeneousdistributedcomputingsystems[J].JournalofParallelanddistributedcomputing, 2001,(6):810-837.

[7]MorenoRJ.Schedulingandresourcemanagementtechniquesindynamicsgridenvironment[A].Proceedingsof8thInt’lConfonAdvancedComputingandCommunications[C].Cochin:ADCOM, 2000.

[8]卜宪宪. 基于小生境和自适应遗传算法的网格任务调度优化研究[J]. 计算机测量与控制，2013, (2):470-479.

[9]王振宇, 李照瑜. 单层树型网格下独立任务的周期性调度[J]. 软件学报, 2013,(2):378-390.

[10]蒲汛,彭喜化,于显平,等.基于均匀离散PSO算法的多QoS网格任务调度策略[J]. 控制与决策,2013，(6):808-814.

(责任编校：晴川)

Grid Cluster Cooperative Dependent Multi Task Scheduling Method Based on Reinforcement Learning and Ant Colony Algorithm

ZHANG Xinhua

(Department of Computer Science，Taiyuan College，Taiyuan Shanxi 030012，China)

Abstract：Current grid cluster resource scheduling method has the disadvantages of long scheduling time, unbalance system load and low CPU utilization rate. A cooperative dependent task scheduling method is proposed, which is based on reinforcement learning and ant colony algorithm. Firstly, the scheduling goal model is defined, then the improved reinforcement learning Sarsa algorithm is used to allocate the task resource, with minimizing the task scheduling time as the goal to get the optimal scheduling method and save the Q value of scheduling method. Then an improved ant colony algorithm is introduce to realize the task allocation to the resource node. The experiment is operated in the Gridsim environment, and the result shows that the method in this paper can realize the cooperative dependent task cluster scheduling, and compared with other methods, it has less task scheduling time, higher CPU usage rate and higher load balance. Therefore, it is a feasible scheduling method suitable for grid environment.

Key Words：cluster scheduling; resource allocation; ant colony algorithm; reinforcement learning

中图分类号:TP393

文献标识码：A

文章编号：1008-4681(2016)02-0050-04

作者简介：张新华(1982— ),女,山西太原人, 太原学院计算机系讲师，硕士.研究方向:计算机应用技术.

收稿日期：2015-12-31