准单色光在光学矢量-矩阵乘法器中的传播与光场分布

周晓霞，张竹娴，杨　丞

(长沙大学电子信息与电气工程系，湖南 长沙 410022)



准单色光在光学矢量-矩阵乘法器中的传播与光场分布

周晓霞，张竹娴，杨丞

(长沙大学电子信息与电气工程系，湖南 长沙 410022)

摘要：研究了光学矢量-矩阵乘法器中光波面的调制特性，从柯林斯公式出发，分析了准单色光在乘法器的空间光调制器平面上的光场分布.结果表明，只使用单个光束会引起空间光调制器上单像素可探测的能量较小，容易出现误差，且焦距比较短，工艺设计困难；采用多光束并束不但可以改善均匀性，使得每个像素可探测的能量显著增加，而且可放宽对所需的焦距限制，从而可降低工艺设计的难度.

关键词：准单色光；柯林斯公式；光学矢量-矩阵乘法器

光学矢量-矩阵乘法器是一种可并行实现一维向量与二维矩阵相乘的光学系统，以光为信息载体可以克服电子计算机串行处理的种种限制，使运算处理的信息量和速度大大提高，利用光的特性还可方便快捷的实现傅里叶变换和小波变换[1].因此作为光学信息处理领域的一个研究热点，利用复合光学系统来实现矢量-矩阵乘法的光学矢量-矩阵乘法器可应用于诸多领域，如光计算、光束整形、频谱分析和匹配滤波等.自从Goodman等[2]在1978年首先提出光学矢量-矩阵乘法器的理论模型以来，该领域的研究引起了国内外学者的广泛关注，目前已经提出了多种结构设计方案并得到了实验验证[3-8]，其发展趋势呈现出运算速度越来越快，体积越来越小，功能越来越强的特点.

作为微型、集成光信息系统中的典型光阵列结构，光学矢量-矩阵乘法器若采用相关光源，干涉和衍射会使得乘法器探测平面上的光强分布不均匀，如何降低或消除干涉、衍射对探测平面上光强分布的影响，对开发高性能高质量的光学矢量-矩阵乘法器具有重要意义.

本文针对线阵列光源发出的准单色光高斯光束(波长范围：845-850nm，中心波长：847nm)通过透镜阵列、柱面透镜阵列、SLM最后聚焦在光电探测器阵列上这一光学矢量-矩阵乘法器的典型物理模型，从结合广义惠更斯-菲涅耳衍射积分公式和矩阵光学的柯林斯公式出发，研究了高斯光束的传输变换特性及SLM接收面上的光场分布.数值分析结果表明，通过多光束并束可以有效地改善激光束对SLM光照的均匀性.

1理论模型

光学矢量-矩阵乘法器的光路原理如图1所示，它主要由光源阵列、球面透镜和柱面透镜组、空间光调制器、光探测器阵列构成.在不考虑系统的像差、色差等因素的理想情况下，实现光学模拟矩阵-矢量相乘.一个m×n矩阵A与一个n维矢量B相乘，得到一个m维矢量C.若分别用aij，bj和ci表示A,B,C的元素，则有

(1)

图1　 光学矢量-矩阵乘法器光路图

为得到ci，用线阵光源来输入矢量B，即使光源线阵中的n个面发射激光器的光强正比于bj(j=1,2…n).另外用一个透射式矩阵编址GaAs/AlGaAs多量子阱(MQW)空间光调制器(SLM)来输入矩阵A，即空间光调制器的m×n个像素按矩阵形式排列，并用电学或光学的写入信号去控制SLM各像素的透射率，使之分别正比于aij.令光源线阵位于准直透镜L的前焦面上，SLM位于柱面透镜CL1的后焦面上，D位于柱面透镜CL2的后焦面上.

光源将会在SLM上形成如下的照度分布：在水平方向(j值变化的方向)上，通过L和CL1，任一bj成像在SLM的第j列处；在垂直方向(i值变化的方向)上，因为CL1在这个方向上不起作用，所以任一bj经L形成平行光.每一bj都会在SLM上形成一条垂直光带，它在垂直方向上的光强是均匀的.即SLM上的任一像素(i,j)的光强分布与i值无关，正比于bj，亦正比于aijbj.准单色光继续传播，经过第二个柱面镜CL2被聚焦到垂直排列的光探测器阵列D上.即在水平方向上，CL2使SLM成一个缩得很小的像，在垂直方向上则CL2不起作用，使得SLM上第i行所有像素的光都集中在第i个探测器上.由于线阵光源上的各个点源发出的光bj互不相干，所以光探测器上第i个探测器器的输出正比于矢量积C的相应元素ci.即满足公式(1).

为方便起见，矩阵A和矢量B的元素都取二进制数，因而只有0和1两个值.矢量B由线阵光源输入，每一个光源元件对应一个矢量的元素，当元素值为1时，令光源发光，当元素值为0时，令相应的光源元件不发光.矩阵A的各元素值由SLM相应像素的透光率表示，当元素值为1时，SLM上对应的像素的透光率为1；当元素值为0时，SLM上对应的像素的透光率为0.

可以看到，在运算的过程中所有的乘法运算和加法运算都是并行地进行的，没有次序上的先后问题.

本文中对光源发出的激光束在SLM上的光场分布进行研究，由于光学矢量-矩阵乘法器中的多束激光是由互相独立的光源发出的，因而任意两束光之间是非相干的，所以我们只需要讨论其中的一束，其它光束的分布只是中心位置不同,最后将它们的强度叠加,就可以得到一个完整的光场分布.考虑由面发射激光器发出的一个激光束，通过同轴的薄透镜、一个相互垂直的正、负柱透镜构成的复合光学系统照射在SLM上，形成矩形光带.将这两个柱面透镜看作是薄透镜，且几乎位于同一位置处.高斯光束先通过柱透镜在x方向扩束，y方向不发生变化.紧接着通过柱透镜在y方向缩小，x方向不发生变化.假设系统处于同一介质中.此处选取空间光调制器像素阵列的列与列之间间距为65μm，而各激光束的成像系统光轴也是相互平行的，光轴之间的间距为65μm.复合柱面透镜系统y方向的尺寸也就被限制在65μm.激光束经过准直照射到复合柱面透镜上的腰斑尺寸也被限制在65μm.在计算中选取经过准直以后的激光束束腰半径为20μm，与复合柱面透镜系统距离为2mm.这时，激光束在复合柱面透镜系统上形成的腰斑恰好是65μm.假设SLM与复合柱面透镜系统之间的距离为4mm.

图2　腰斑大小随着柱透镜焦距f变化的曲线

从上图可以看出，当焦距很小的时候，在SLM上形成很大的腰斑，随着焦距的增加，成像腰斑逐渐减小.当焦距刚好等于柱透镜面上的等相位面曲率半径时，成像腰斑达到最小，恰好等于透镜面上入射光束的光斑半径，即65μm.利用这一特性，我们可以做到在x方向上的扩束，而在y方向成像腰斑为65μm.由此我们选取y方向焦距为2000μm，x方向焦距为300μm.

由于光学矢量-矩阵乘法器所使用的器件实际上尺寸都是有限的，因此必须考虑它们的衍射作用.

马吕斯定理指出，任何没有像散的成像系统中，沿任何成像路径所测量的光程应该相等.在直角坐标系下，光学系统的程函数可用矩阵元素表示为[9]：

(2)

式中L(x1,y1,x2,y2)表示两个参考平面上离光轴距离分别为x1,y1、x2,y2的两点P1P2间的光路程，L0为沿光轴上的光程.将上式代入菲涅耳衍射积分式，得到轴对称傍轴光学系统的柯林斯公式[10]

(3)

式中U1(x1,y1)为光学系统入射平面上的光波复振幅，U2(x2,y2)为光波穿过光学系统后在出射平面上的光波复振幅.傍轴光学系统中柯林斯公式是菲涅耳衍射积分的推广，可以一次计算出光波通过ABCD傍轴光学系统的衍射场，而菲涅耳衍射积分只能计算光波在介质空间中衍射平面后满足傍轴条件的光波场.

(4)

(5)

忽略后两项以及与能量无关的相位因子，得到[11]

(6)

式(6)的形式说明，衍射光波场的分布是照明光波场的振幅按照几何光学传播规律到达观察平面后受函数ΦF(x,y)“调制”的结果.所以将ΦF(x,y)称为菲涅耳衍射振幅调制函数.

我们知道了光波场的振幅分布，那么很容易就可以求出光场的强度分布：

(7)

2数值计算和讨论

图3　单光束时成像面SLM上1比特位的几何光强分布

图4　直接应用ABCD定理得到的单光束时

很明显通过复合柱面系统变换后，光场仍是一个高斯分布图像.

考虑衍射作用，引入菲涅耳衍射调制函数，利用公式(6)可以算出衍射光场分布.当取复合柱面透镜系统的尺寸孔径y方向为65μm、x方向为100μm时，光强分布如图5、6所示.

图5　单光束时SLM上1比特位的衍射光强分布

图6　单光束时SLM上1比特位的

由图6可以看出，在x方向的光场分布与几何光学的结果图4相比较，有明显的差异.在计算中采用柯林斯公式对光场分布进行计算，引入菲涅耳衍射因子后，得到的衍射场实际上是几何图像与菲涅耳衍射因子的乘积，图7给出了x方向的菲涅耳衍射因子分布.

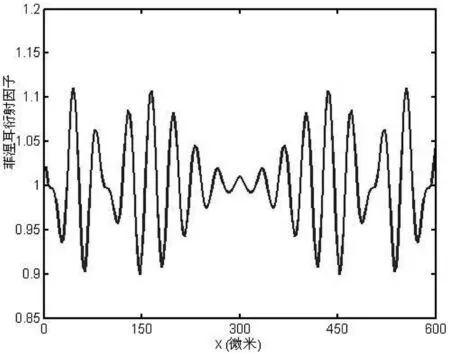
图 7　X方向的菲涅耳衍射因子

对比上面三个图：几何光学结果是上凸的高斯分布(图4)，菲涅耳衍射因子在单位1附近震荡变化(图7).当选用的器件尺寸较小，造成的孔径光阑较小时，菲涅耳衍射因子的轮廓线在中心附近是下凹的，衍射光场在x方向投影轮廓线则在中心附近几乎是一个平顶(图6).虽然考虑衍射后的光场分布与几何光学结果有着较大差异，但是均匀性还是有所改善.由于在x方向光束被“拉伸”得很厉害(八倍左右)，造成的影响有：(1)每个像素可探测的能量很小，容易出现误差；(2)边缘和中间平顶之间的差距过大(图6)；(3)光束拉伸要求的放大率很大，使得x方向的焦距比较短，从而在工艺设计上易造成很大的困难.

激光多种应用领域的研究表明，在多束激光束的并合光束照明时，光斑的强度分布均匀性较单光束照明时显著提高[12-14].选取垂直腔面发射激光器(VCSEL)为光源，因为VCSEL易于实现高密度二维面阵的集成、制作成本低廉，所以可以考虑用多光束并合取代单束光照射，获得较理想的光束分布.

图 8　五束光照射时在SLM上一比特位的衍射场

当使用单光束成像时，在x方向将光束扩展，在SLM上形成600μm长、60μm宽的光带.而当使用多光束成像时，在SLM上要形成同样长宽的光带，每一束光的扩展相应减小，通过优化(3，5，7束比较，当然光束越多，得到的均匀性越好)我们采用五束光，令每束光在SLM上形成160μm长、60μm宽的光带(光束扩展越大，衍射越明显)，束与束之间相距120μm.根据图2中给出的曲线，160μm时对应fx=800μm左右.在y方向的成像腰斑为60μm，如图2对应的fy仍然保持约为2000μm.下面就给出五束光照射时在SLM上一比特位的衍射场：

为了进一步研究改善均匀性，我们做出了五束光情况下在成像面上x方向1000μm和600μm范围内的几何光场分布.

图9　五束光照射时在SLM上一比特位在

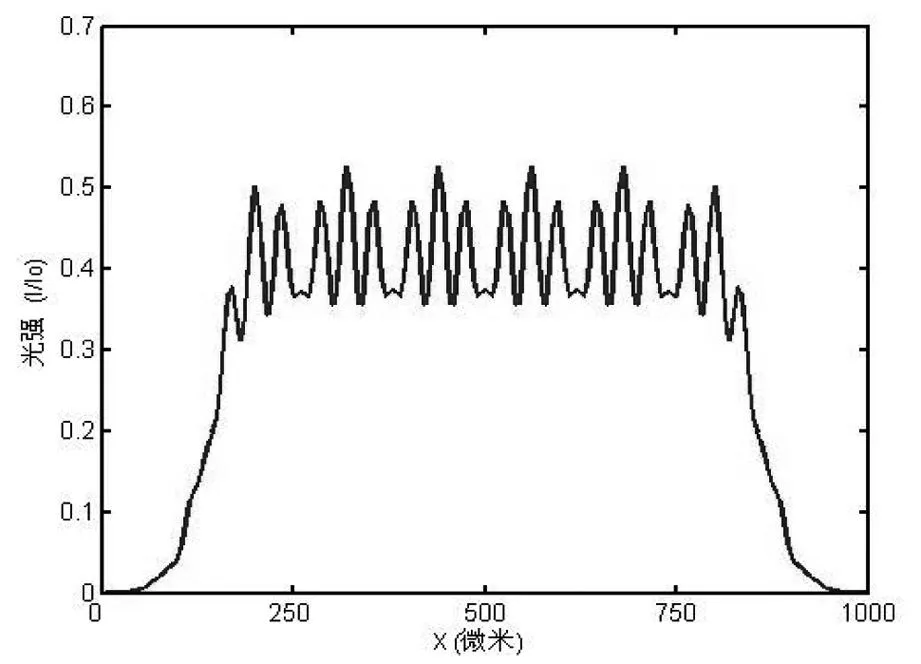
图10　五束光照射时在SLM上一比特位在

从上图可以看出在一段范围内出现了近似的平顶，这与单光束的高斯分布相比，无疑有效改善了均匀性.可见采用多光束不但可以改善均匀性，而且改善了由于在x方向光束被“拉伸”得很厉害所造成的影响：一是使得每个像素可探测的能量显著增加，减小了能量损失；(2)光场波动不大，基本在0.35～0.5区间震荡；(3)对于满足x方向同样的光束拉伸要求，需要的放大率减小，使得x方向的焦距增加，从而降低了设计困难.

3结论

本文从柯林斯公式出发对光学矢量-矩阵乘法器的光束变换特性进行了研究.结果表明由于衍射的影响，空间光调制器平面上的光场分布与几何光学结果有着较大差异，对单光束来说，光束边缘和中间平顶之间的差距过大，每个像素可探测的能量较小，容易出现误差，光束拉伸要求的放大率较大，要求焦距比较短，工艺设计困难；采用多光束并束不但可以改善均匀性，使得每个像素可探测的能量显著增加，而且需要的放大率减小，使得要求的焦距增加，从而降低了设计困难.

参考文献：

[1] Gruber M, Jahns J, Sinzinger S. Planar-integrated optical vector-matrix multiplier[J].Appl Opt,2000,(29):5367-5373.

[2] Goodman J W, Diaz A R, Woody L M. Fully parallel, high speed incoherent optical method for performing discrete Fourier transforms[J].Opt Lett,1978,(1):1-3.

[3] Caulfield H J, Rhodes W T, Foster M J, et al. Optical implementation of systolic array processing [J].Opt Commun,1981, (40):86-90.

[4] Mosca E P, Griffin R D, Pursel F P, et al. Acousto—opticalmatrix—vectorproductprocessor [J].Appl Opt,1989,(18):3843-3851.

[5] 金翊,何华灿,吕养天.三值光计算机基本原理[J].中国科学E辑,2003,(2):111-115.

[6] 李梅,金翊,何华灿,等.基于三值逻辑光学处理器实现向量矩阵乘法[J].计算机应用研究,2009,(8):2839-2841.

[7] 王先超,姚云飞,陈蕴.一种新的光学向量-矩阵乘法[J].计算机工程与应用,2011,(6):34-37.

[8] 卢洋洋,周平,朱巍巍,等.基于光学向量矩阵乘法器的光学信息处理系统研究[J].光电子激光,2013,(9):1656-1661.

[9] Gerrard A, Burch J M. Introduction to Matrix Methods in Optics[M].New York: Dover Publication Inc., 1975.

[10] Born M, Wolf E. 光学原理(第7版)[M]. 杨葭荪,译.北京：电子工业出版社,2009.

[11] Goodman J W.傅里叶光学导论(第3版) [M]. 秦克诚,刘培森,陈家璧,等译.北京：电子工业出版社,2011.

[12] 李宾中. 多束激光的并合、传输变换与照明特性研究[D].成都：四川大学博士学位论文,2002.

[13] 谢静雅,李新碗,陈建平.基于半导体光放大器的光学向量矩阵乘法器的实现方法[J]. 光电子·激光,2012,(4)：654-658.

[14] 卢洋洋,田永辉,杨林.Integrated reconfigurable optical add-drop multiplexers based on cascaded microring resonators[J]. Journal of Semiconductors,2013,(9):86-91.

(作者本人校对)

Quasi-monochromatic Light Propagation and Optical Field Distribution in Optical Vector Matrix Multiplier

ZHOU Xiaoxia, ZHANG Zhuxian, YANG Cheng

(Department of Electronic Information and Electrical Engineering, Changsha University,Changsha Hunan 410022, China)

Abstract：In this paper, using the Collins formula, the modulation properties of the quasi-monochromatic light through an optical vector-matrix multiplier have been studied, and the optical field distributions in the plane of spatial light modulator are analyzed in detail. Results show that single beam design is easy to cause errors, because the energy detected by each pixel on the spatial light modulator is small. And the single beam design requires relatively short focal length, which leads to some design difficulties. By using multi beam design, the uniformity of the light field distribution can be improved, so that the energy detected by each pixel can be much higher. It can also broaden the limit of focal length, which can reduce the difficulty of the process design.

Key Words：quasi-monochromatic light; Collins formula; optical vector matrix multiplier

中图分类号:TN248.4

文献标识码：A

文章编号：1008-4681(2016)02-0026-05

作者简介：周晓霞(1981— )，女，江苏盐城人，长沙大学电子信息与电气工程系讲师，硕士.研究方向：光子晶体、光学超材料.

基金项目：国家自然科学基金(批准号：61308005)资助项目；湖南省教育厅一般项目(批准号：15C0126)；长沙市科技计划 (批准号：K1407008-11).

收稿日期：2015-12-24