基于偏最小二乘法的土壤有机碳高光谱预测研究

马　丽,　吕成文,　唐　炎

(安徽师范大学 国土资源与旅游学院,安徽 芜湖　241000)



基于偏最小二乘法的土壤有机碳高光谱预测研究

马丽,吕成文,唐炎

(安徽师范大学 国土资源与旅游学院,安徽 芜湖241000)

摘要：对86个土壤样品高光谱数据进行平滑去噪、一阶微分变换以及多元散射校正处理，在此基础上，建立土壤有机碳含量的偏最小二乘法(PLS)反演模型.结果表明，获得的五种PLS模型均具有较高的模型精度.其中，主成份个数为10时，R+MSC的PLS模型效果最好.校正模型的决定系数R2=0.95，校正均方根误差RMSEC=0.95.验证模型的决定系数R2=0.78，预测均方根误差RMSEP=2.03.利用PLS模型对预测集进行预测，实测值与预测值的决定系数R2=0.83，预测均方根误差RMSEP=1.71，预测标准差SEP=1.73.PLS模型可以对土壤有机碳含量进行预测.

关键词：高光谱；偏最小二乘法；土壤有机碳

土壤被认为是农业生态服务系统中最主要的贡献因子，是水土资源与环境模拟等研究的基本参数[1].在环境监测、模型预测及精准农业中需要成本低且质量高的土壤数据，而传统的土壤数据获取费时费力且昂贵[2].要解决这一问题就必须要对土壤进行快速准确的测定与评价.近年来，高光谱技术在土壤属性定量分析中获得了快速发展[3].国内外的许多学者通过各种方法建立土壤有机碳与高光谱反射率之间的反演模型，常用的方法有多元线性回归、主成分回归、人工神经网络、支持向量机等[4-7].王超等利用多元逐步回归统计方法进行了土壤有机质信息波段的提取和监测模型的构建[8].姚慧等利用三个中心波段的有机质诊断指数与有机质含量分别进行回归分析[9].然而这些方法仅使用光谱数据中部分特征波段代替整个光谱数据，造成了光谱信息的损失，丢弃了一些对有机碳含量反演有用的信息.偏最小二乘法(PLS)是解决这一问题的有效方法，它可以利用全谱数据进行分析，且对样本容量要求不高，对自变量多、变量间存在多重相关性的情况具有独特的优势[10]，适合于土壤高光谱数据的处理.本文拟探讨基于土壤高光谱数据结合偏最小二乘法(PLS)实现对农田土壤有机碳含量的快速测定与评价，以期为环境监测、精准农业等相关研究提供参考.

1材料与方法

1.1土壤样品的采集与处理

土壤样品采集于安徽省淮南市和蚌埠市相接壤的沿淮平原区，采集时间为2014年3月，沿公路两侧且距离公路至少100m外采集，采样间隔大于100m，在采集过程中使用GPS定位，记录采样点的坐标以及土地利用等信息，在其周围2×2m范围内再设置4个采样点，取每个样本点0-15cm深度的表层土壤混合，获得一个土样，取500g左右，装入布袋中，共86个土样.土样置室内风干、研磨，分别过20目(1mm孔径)和100目(0.149mm孔径)的筛子，过20目(1mm孔径)筛的土样用于实验室土壤高光谱测量，过100目(0.149mm孔径)筛的土样用于土壤有机碳含量测定.实验室测定的土样有机碳含量统计特征值见表1.

表1　有机碳含量统计特征值

1.2光谱数据获取

使用荷兰Avantes公司生产的型号分别为Avaspec-2048×14、Avaspec-NIR256-2.5的两种地物光谱仪进行测量.其中Avaspec-2048×14光谱仪光谱范围为188-1170nm，光谱分辨率2.4nm，光谱采样间隔0.6nm.Avaspec-NIR256-2.5的光谱范围是928-2528nm，光谱分辨率10nm，光谱采样间隔6nm.两种光谱仪输出光谱曲线均设定由10条原始扫描光谱自动平均所得.土壤样品置于深2cm，直径8cm的器皿中，用直尺刮平土样表面.光源为4×25w的环形光源.8°视场角的光纤探头，探头垂直置于土壤样品表面上方20cm处.每一个土壤样品测量前均使用标准白板进行定标，同时每个土壤样品从四个不同方向进行光谱曲线的获取，进行算术平均后得到该土样的高光谱反射率数据.

1.3光谱数据预处理

为了减少噪音，提高信噪比，压缩数据量，对光谱数据进行平滑处理.本研究采用9点移动平均法对光谱曲线进行平滑去噪处理，得到平滑后的原始光谱反射率数据(Original reflectance, R).为了进一步消除无关信息，充分挖掘高光谱数据中的有效信息，对平滑后的数据进行一阶微分(First derivative scattering, FDR)及多元散射校正(Multiplicative scatter correction, MSC)处理.使用Savitzky-Golay卷积求导法对高光谱原始数据R进行求导，求导后的一阶微分光谱曲线如图1所示，从中可看出光谱反射率曲线的波段特征更为明显，尤其是1370nm和1880nm波段处的吸收谷及1960nm波段处的反射峰，显著提高了土壤光谱反射率与有机碳含量的相关性.多元散射校正(MSC)处理后的光谱曲线如图2所示，其可以去除近红外漫反射光谱中样品的镜面反射及不均匀性造成的噪声，消除漫反射光谱的基线及光谱的不重复性，使图像更紧凑，提高原光谱数据的信噪比.

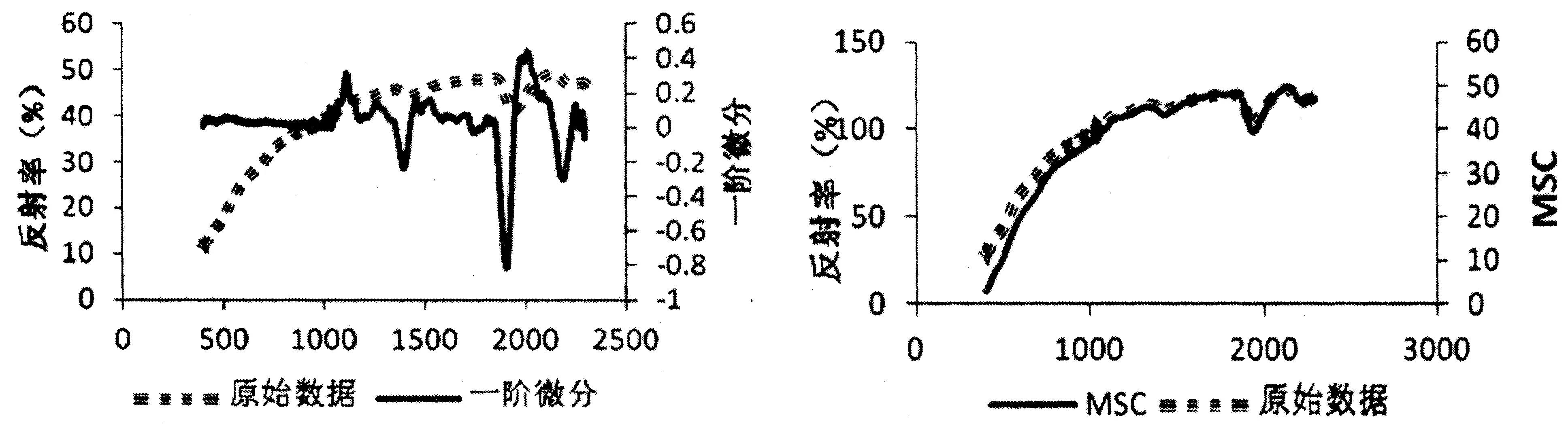
图1　原始光谱一阶微分光谱曲线　　　　　　　　　　　　图2　原始光谱及MSC光谱曲线图Fig.1　Original spectrum and first　　　　　　　　　　　　　　Fig.2　Original spectrum andderivative scattering correction　　　　　　　　　　　　　　　　multinle reflectance snectrum

基于上述预处理，并参照相关文献[11]，设置五种光谱预测方案，见表2.

1.4偏最小二乘法(PLS)

偏最小二乘法(PLS)是基于因子分析的多变量校正方法，可以同时实现回归建模、数据结构简化以及两组变量之间的相关性分析. 其原理与主成分分析很相似，假设矩阵X及矩阵Y，主成分只对矩阵X进行分解，消除无用的噪音信息，而偏最小二乘法既对矩阵X分解，提取相关有用信息，也对矩阵Y进行分解，且在分解矩阵X的同时考虑矩阵Y的影响[12].因此，PLS所提取的成分既能很好地概括自变量系统中的信息，又能最好地解释因变量，并排除系统中的噪音干扰[13].

表2　五种光谱预测方案

以单因变量为例阐述其基本建模思想[10,14]：设有因变量y和k个自变量{x1,x2,…,xk}，样本数为n，构成因变量和自变量的数据表x[x1,x2，…,xk]n×k和y=[u]n×1，在x中提取一个主成分t1，t1是x1，x2，…，xk的线性组合，要求t1尽可能多的携带x中的变异信息，同时与y的相关性最大，提取第一个主成分t1后，实施y和x对t1的回归，如果此时回归方程达到满意的精度，则算法停止.否则，利用x和y被t1解释后的残余信息进行第二轮的主成分提取.如此反复，直到能达到一个较为满意的精度为止.若最终对x提取了m个主成分t1，t2，…，tm，偏最小二乘回归将实施y对t1，t2，…，tm的回归，然后再表达成y对原变量x的回归方程.

1.5模型的评价指标

模型的评价指标常用的有均方根误差(RMSE)和决定系数(R2)，均方根误差越小，模型的效果越好，决定系数越接近1，效果越好.好的校正模型及验证模型对应较低的均方误差(RMSE)和较高的决定系数R2.校正模型对验证集预测结果的好坏也是由预测均方根误差(RMSEP)和决定系数判定，好的预测结果同样对应较低的预测均方根误差(RMSEP)和较高的决定系数(R2).此外，预测集标准差(SEP)也常用于模型预测的评价，预测标准差越小，模型的预测结果越好.

2结果与分析

2.1模型的构建

对采样获得的86个样本数据，随机选取61个用于建立预测模型，剩余的25个用于评价所建预测模型的稳定性和准确性.根据偏最小二乘法原理，模型的构建不需要全部主成分因子参与，而只要选取合适的主成分因子(最适主因子)，就可以得到一个预测效果很好的模型.本研究采用交互验证法(cross validation)确定主成分最佳因子数，并根据残余方差和判定最佳主成分因子个数.一般来说，主成分因子数过少不能充分反映光谱特征信息，过多则可能含有过多的噪音信息.具体计算过程：对于参加建模的N个样本，每次选择n个作为预测样本，剩下的N-n个作为建模样本，用来建立模型用以预测这n个样本，重复上述过程，直到N个样本都被且仅被预测过一次时，得到的最小的预测值与真实值的差的平方和的值，即残余方差和最小，便可确定最佳的预测模型.

建模过程在Unscrambler9.7软件中完成，各方案建模结果见表3.

表3　5种方案的PLS模型结果比较

由表可知，总体来看，五种方案获得的PLS模型均具有较高的模型精度.其中，校正模型效果最好的是R+MSC的PLS模型，决定系数R2=0.95，校正均方误差RMSEC=0.95.其次是原始数据R与R+FDR的PLS模型，模型效果相同，决定系数均为R2=0.94，校正均方误差RMSEC=1.02.然后是一阶微分(FDR)的PLS模型，决定系数R2=0.94，校正均方误差RMSEC=1.01.最后是多元散射校正(MSC)的PLS模型，决定系数R2=0.92，校正均方误差RMSEC=1.17.

而验证模型效果最好的是多元散射校正(MSC)的PLS模型，决定系数R2=0.79，预测均方误差RMSEP=1.90.其次是原始数据R与R+FDR的PLS模型，决定系数均为R2=0.78，预测均方误差均为RMSEP=2.01.再次是R+MSC的PLS模型，决定系数R2=0.78，预测均方误差RMSEP=2.03.最后是一阶微分(FDR)的PLS模型，决定系数R2=0.71，预测均方误差RMSEP=2.30.

以上结果表明，各方案建立的校正模型效果均较好.其中，R+MSC建立的校正模型精度最高，建模效果最好.

2.2模型的检验

将预测集中的25个样本代入建好的模型中，对预测集中的有机碳含量进行预测，结果见表4.

可知模型的预测效果均较好，其中R+MSC的模型预测决定系数R2=0.83，误差均方根RMSE=1.71，预测标准差SEP=1.73，效果最好.原始数据R的模型预测决定系数R2=0.83，误差均方根RMSE=1.81，预测标准差SEP=1.84.一阶微分(FDR)预测模型决定系数R2=0.81，误差均方根RMSE=2.13，预测标准差SEP=1.98.多元散射校正(MSC)模型预测决定系数R2=0.82，误差均方根RMSE=1.66，预测标准差SEP=1.68.R+FDR的预测模型决定系数R2=0.83，误差均方根RMSE=1.80，预测标准差SEP=1.84.可用于土壤有机碳含量的预测.

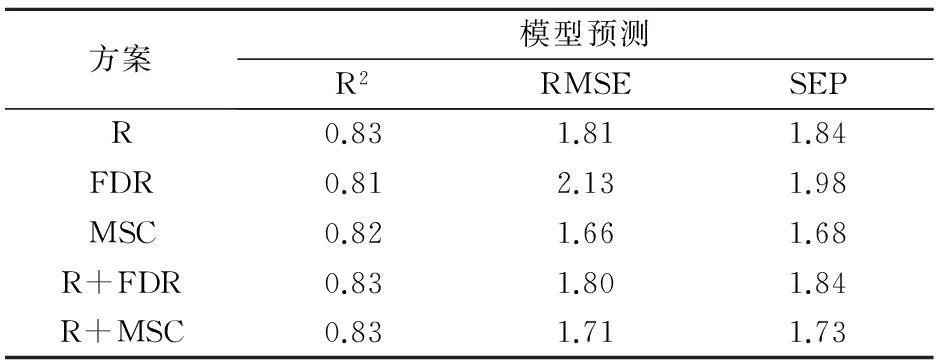
表4　预测集的模型比较

3结论

根据光谱预测方案，结合偏最小二乘法(PLS)对土壤高光谱数据进行定量反演，五种方案模型预测效果均较好.其中，校正模型效果最好的是R+MSC结合的PLS模型，决定系数R2=0.95，校正均方误差RMSEC=0.95.模型验证效果最好的也是R+MSC结合的PLS模型，预测决定系数R2=0.83，误差均方根RMSE=1.71，预测标准差SEP=1.73.偏最小二乘法可以实现农田土壤有机碳含量的快速测定与评价，为环境监测、精准农业等相关研究提供参考.

参考文献：

[1]SANCHEZ PA, AHAMED S, CARRé F, et al. Digital soil map of the world[J]. Science, 2011,325:680-681.

[2]GOMEZ C, ROSSEL AR, McBratney AB. Soil organic carbon prediction by hyperspectral remote sensing and field vis-NIR spectroscopy: An Australian case study[J].Geoderma,2008,(146):403-411.

[3]汪善勤,舒宁.土壤定量遥感技术研究进展[J].遥感信息,2007,(6):89-93.

[4]李启权,王昌全,岳天祥，等.基于定性和定量辅助变量的土壤有机质空间分布预测——以四川三台县为例[J].地理科学进展,2014,33(2):269-268.

[5]LU P, WANG L, NIU Z, et al. Prediction of soil properties using laboratory VIS-NIR spectroscopy and Hyperion imagery[J]. Journal of Geochemical Exploration,2013,132:26-33.

[6]陈红艳,赵庚星,李希灿，等.基于小波变换的土壤有机质含量高光谱估测[J].应用生态学报,2011,22(11):2935-2942.

[7]纪文君,李曦,李成学，等.基于全谱数据挖掘技术的土壤有机质高光谱预测建模研究[J].光谱学与光谱分析,2012,32(9):2393-2398.

[8]王超,冯美臣,杨武德，等.麦田耕作层土壤有机质的高光谱监测[J].山西农业科学,2014,42(8):869-873.

[9]姚慧,吕成文,刘程海，等.宣城市岗坡地土壤有机质含量光谱预测分析[J].安徽师范大学学报,2011,34(5):472-474,484.

[10]张恒喜,郭基联,朱家元，等.小样本多元数据分析方法及应用[M].西安:西北工业大学出版社,2002.

[11]刘雪华,孙岩,吴燕.光谱信息降维及判别模型建立用于识别湿地植物物种[J].光谱学与光谱分析,2012,32(2):459-464.

[12]陆婉珍.现代近红外光谱分析技术[M].北京:中国石化出版社,2006：44.

[13]杜发兴,徐刚.偏最小二乘回归模型在城市需水预测中的应用[J].水力发电,2008,34(6):20-23.

[14]罗批,郭继昌,李锵，等.基于偏最小二乘回归建模的探讨[J].天津大学学报,2002,35(6):783-786.

Soil Organic Carbon Prediction by Hyperspectral Based on Partial Least Squares Regression

MA Li,LYU Cheng-wen,TANG Yan

(College of Territorial Resources and Tourism, Anhui Normal University, Wuhu 241000, China)

Abstract：The hyperspectral data of 86 soil samples were preprocessed with smoothing, first derivative reflectance (FDR) and multiple scattering correction (MSC). SOC contents were predicted by partial least squares regression using original data and pretreatment data. Results showed that the precision of five PLS models were all good. When the principal component number was 10, the model that original data being combined with MSC is suited. For the calibration mode, the determination coefficient (R2) is 0.95, root mean square error of calibration (RMSEC) is 0.95. For the verification model, the corresponding values were 0.78 and 2.03. After prediction set was predicted, the determination coefficient between measured and predicted values was 0.83 with root mean square error and standard error of prediction was 1.71 and 1.73. PLS model can predict SOC contents using hyperspectral.

Key words:hyperspectral; PLS; SOC

中图分类号：TP79

文献标志码：A

文章编号：1001-2443(2016)01-0164-04

作者简介：马丽(1989-)，女，安徽定远人，硕士研究生，主要从事遥感技术应用研究.

基金项目：国家自然科学基金(41371229).

收稿日期：2014-12-08

DOI：10.14182/J.cnki.1001-2443.2016.02.013

引用格式：马丽，吕成文，唐炎.基于偏最小二乘法的土壤有机碳高光谱预测研究[J].安徽师范大学学报：自然科学版，2016，39(1)：164-167.