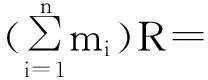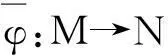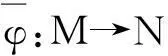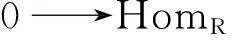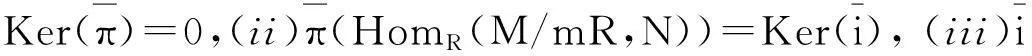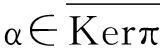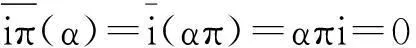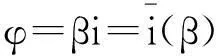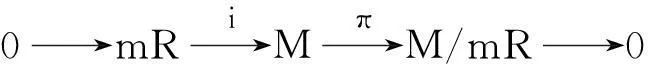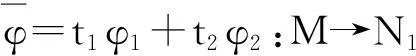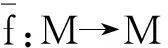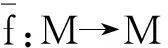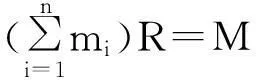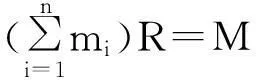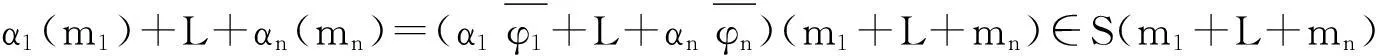SPQ-内射半模

曾慧平，黄福生

(1.南昌航空大学 科技学院，江西 南昌　330034；2.江西师范大学 数学与信息科学学院，江西 南昌　330022)



SPQ-内射半模

曾慧平1，黄福生2

(1.南昌航空大学 科技学院，江西 南昌330034；2.江西师范大学 数学与信息科学学院，江西 南昌330022)

摘要：设是右-半模，半模称为内射的，若任意的small-主子半模到的同态可扩张至到的同态.若是内射的，则称是内射半模.本文给出了内射半模的定义并刻画其相应性质.

关键词：small-子半模；内射半模；自同态半环

引言

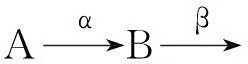
设R是半环.左R-半模称为p-内射的[3]，如果对任意R的主左理想到M的同态可扩张至R到M的同态.一个左R-模M称为左small-内射的[4，5]，如果每个从R的small左理想到M的左R-模同态可以扩张至R到M的同态.在p-内射半模和small-内射模概念的基础上，本文给出了SPQ-内射半模的定义并刻画其相应性质.

1SPQ-内射半模

定义1.1[1]设K是M的子半模.若M的子半模L满足L+K=M，必可得L=M，则称K是M的small-子半模.记为K=M.

定义1.2[1]设m∈M，则mR={mr|r∈R}称为M的主子半模.

引理1.3设K=M且f:M→N是半模同态，则f(K)=N.

证明：设L

定义1.5设M，N是右R-半模，半模N称为SP-M-内射的，若任意M的small-主子半模到N的同态可扩张至M到N的同态.

定义1.6若M是SP-M-内射的，则称M是SPQ-内射半模.

定理1.7设M，N是右R-半模.若HomR(M,N)m=lNrR(m)，其中m∈M，满足mR=M，则N是SP-M-内射的.

定理1.8设R是含加法逆元的半环，M，N是右R-半模.N是SP-M-内射的当且仅当∀m∈M，满足mR=M，HomR(M,N)m=lNrR(m).

“⟸”由定理1.7直接可得.

定理1.9设M是投射半模，则下列命题等价：

(1)M的任意small-主子半模都是投射的；

(2)SP-M-内射半模的商半模是SP-M-内射的；

(3)内射半模的商半模是SP-M-内射的.

证明：(1)⟹(2)设N是SP-M-内射的，X

(2)⟹(3)显然成立.

(3)⟹(1)证明过程同(2)⟹(1).

定理1.10设M,N，右R-半模，则下列命题等价：

(1)N是SP-M-内射半模;

(2)⟹(1)由定义直接可证．

推论1.11M是SPQ-内射半模当且仅当对任意短真正合列

其中m∈M满足mR=M,i,π分别为自然嵌入映射和自然满射，序列

证明：只需令N=M即可.

定理1.12SP-M-内射半模的任意直和项仍然是SP-M-内射的.

证明：设N是SP-M-内射半模，N=A⊕A′.m∈M满足mR=M且f:mR→A是半模同态.定义g:mR→N为g(mr)=(f(mr),0，∀r∈R.不难验证g是半模同态，故g可以扩张到同态g′:M→N.记πA:N→A是自然投射，则πAg′:M→A满足πAg′|A=f，从而A是SP-M-内射半模.

定理1.13设Ni(1≤i≤n)是SP-M-内射半模，则⊕ani=1Ni是SP-M-内射的.

2自同态半环与SPQ-内射半模

没有特别声明，文中此部分S均指S=EndR(M).

引理2.1设M是右R-半模，则下列命题等价：

(1) lMrR(m)=Sm,∀m∈M满足mR=M；

(2) 若rR(m)⊆rR(n)，其中m,n∈M且mR=M，则Sn⊆Sm.

证明：(1)⟹(2)若rR(m)⊆rR(n)，其中m,n∈M且mR=M，则lMrR(n)⊆lMrR(m).因为Sn⊂lMrR(n)且由(1) lMrR(m)=Sm，，即可得Sn⊆Sm.

(2)⟹(1)设m∈M满足mR=M，且令x∈lMrR(m)，则rR(m)⊆rR(x).由(2)可知，Sx⊆Sm.即存在φ∈S，使得x=φ(m)，从而x∈Sm，lMrR(m)⊆Sm.Sm⊆lMrR(m)显然成立，得证.

推论2.2若rR(m)⊆rR(n)，其中m,n∈M且mR=M，必可得Sn⊆Sm，则M是SPQ-内射半模.

证明：由定理1.7及引理2.1直接可得.

推论2.3设R是含加法逆元的半环，M是右R-半模，则下列命题等价：

(1) M是SPQ-内射半模；

(2) lMrR(m)=Sm，∀m∈M满足mR=M；

(3) 若rR(m)⊆rR(n)，其中m,n∈M且mR=M，则Sn⊆Sm.

证明：由定理1.8及引理2.1直接可得.

定理2.4设R是含加法逆元的半环，M是SPQ-内射半模.若M=m0R，m0∈M且α∈S满足α(M)=M，则lSKer(α)=Sα.

证明：Sα⊆lSKer(α)显然成立,下证lSKer(α)⊆Sα.令β∈lSKer(α)，rR(α(m0))⊆rR(β(m0))，从而lMrR(β(m0))⊆lMrR(α(m0)).由于α(M)=α(m0)R=M，由推论2.3可得Sβ(m0)⊆lMrR(β(m0))⊆lMrR(α(m0))=Sα(m0).故β(m0)=γα(m0)，γ∈S，即β=γα，β∈Sα，得证.

定理2.5设R是含加法逆元的半环，M是SPQ-内射半模，m,n∈M且mR=M.若存在单同态f:mR→nR，则必存在满同态σ:Sn→Sm.

定理2.6设M是SPQ-内射半模，m,n∈M且mR=M.若存在满同态f:mR→nR，则必存在单同态σ:Sn→Sm.

推论2.7设R是含加法逆元的半环，M是SPQ-内射半模，m,n∈M且mR=M.若mR;nR，则Sm;Sn.

定理2.8设M是SPQ-内射半模且mi∈M满足miR=M(1≤i≤n).

(1) 若Sm1⊕L⊕Smn是直和，则对任意半模同态α:m1R+L+mnR→M在S=EndR(M)中存在同态扩张.

(2) 若m1R⊕L⊕mnR是直和，则S(m1+L+mn)=Sm1+L+Smn.

即证得Sm1+L+Smn⊆S(m1+L+mn).S(m1+L+mn)⊆Sm1+LSmn显然成立.

参考文献：

[1]GOLAN J S. Semirings and their applications[M].L ONDON:KLUWER ACADEMIC PUBLISHERS,1999.

[2]CHEN Peici. Semiring theory and languages automata[M]. Nanchang: Jiangxi Gao xiao press, 1993.

[3]黄福生,杨俊燕,余安安. p-内射半模[J].南昌大学学报：理科版,2011,35(2):111-114.

[4]余祖俊,吴俊.small-内射模的某些研究[J].安徽师范大学学报：自然科学版,2009,32(4):325-327.

[5]曾慧平,黄福生,肖贤民.i-内射半模[J].江西师范大学学报：自然科学版,2007,31 (5):488-491.

[6]肖贤民，黄福生，曾慧平．关于正向极限的一些性质[J]．华东交通大学学报，2007，24(4)，152-154.

[7]曾慧平,黄福生,肖贤民.i-内射半模的Hom函子刻画[J].南昌大学学报：理科版,2008,32(4):327-329.

[8]王聪,黄福生.拟内射半模与伪内射半模.江西师范大学学报：自然科学版,2012,36(2):155-159.

SPQ-Injective Semimodules

ZENG Hui-ping1,HUANG Fu-sheng2

(1.Science and Technology College, Nanchang Hangkong University， Nanchang 330034, China; 2.College of Mathematics and Informaticson Science, Jiangxi Normal University, Nanchang 330022, China)

Abstract:Let M be a right R-semimodule. A right R-semimodule N is called SP-M-injective if, every R-homomorphism from a small and principal subsemimodule of M to N can be extended to an R-homomorphism from M to N. If M is SP-M-injective semimodule, then M is called SPQ-injective semimodule. In this paper we give some characterizations and properties of SPQ-injective semimodules.

Key words:small-semimodules; SPQ-injective semimodules； endomorphism semirings

中图分类号：O153.3

文献标志码：A

文章编号：1001-2443(2016)02-0120-04

作者简介：曾慧平(1983-)，女，讲师，理学硕士，主要从事半环理论的研究.

基金项目：国家自然科学基金(11261021)；江西省教育厅青年科学基金(No.GJJ14541).

收稿日期：2014-06-06

DOI：10.14182/J.cnki.1001-2443.2016.02.004

引用格式：曾慧平，黄福生.SPQ-内射半模[J].安徽师范大学学报：自然科学版，2016，39(2)：120-123.