一般大气环境下钢筋混凝土构件抗震性能时变特征*

梁　岩，陈　淮，罗小勇

(1.郑州大学 土木工程学院，河南 郑州　450001；2.中南大学 土木工程学院，湖南 长沙　410075)



一般大气环境下钢筋混凝土构件抗震性能时变特征*

梁岩1†，陈淮1，罗小勇2

(1.郑州大学 土木工程学院，河南 郑州450001；2.中南大学 土木工程学院，湖南 长沙410075)

摘要：采用精细化有限元全过程分析方法，考虑混凝土碳化、钢筋锈蚀及其引起的粘结滑移性能退化等多因素耦合作用，研究在一般大气环境使用年限内，耐久性退化对构件抗震性能的影响规律和内在机理.结果表明，一般大气环境下，钢筋混凝土构件使用年限在30 a内抗震性能变化不大.当使用年限超过30 a后，抗震性能显著退化.当使用100 a时，承载力降低22.5%，刚度约退化33.5%，延性降低36.7%，耗能能力降低40.5%.建议在一般大气环境下对钢筋混凝土构件进行抗震设计时，应考虑随使用年限的增长，耐久性退化对抗震性能的影响，从而保证结构良好的抗震性能.

关键词：钢筋混凝土；耐久性；抗震；时变特征；一般大气环境

钢筋混凝土结构在设计使用年限内，由于材料老化、不利环境及使用不当等因素影响，结构常出现不同程度的损伤，这种损伤积累直接导致结构耐久性降低、承载力下降、抗震性能退化[1].中国传统设计考虑混凝土结构的耐久性不足，设计的安全度设置水平较低，留下了大量存在一定缺陷的结构[2].一般大气环境下，混凝土碳化及其引起的钢筋锈蚀是造成结构耐久性退化的主要因素.实际钢筋混凝土结构的耐久性具有时变特征,任其发展会由量变积累引起质变,地震中完全有可能引起承载力不足,甚至导致结构解体或倒塌.对于钢筋混凝土结构问题更为突出的是许多结构在处于严重腐蚀环境之中的同时又处于地震多发地带[3].对耐久性退化钢筋混凝土结构抗震性能的研究始于1988年Kyioshi等[4]通过喷洒盐水的方法使混凝土梁中的钢筋锈蚀，进行低周反复荷载试验，结果表明，在循环荷载作用下，结构承载力较无锈蚀时降低速度快.之后国内外学者对钢筋混凝土结构耐久性损伤后的抗震性能进行了大量的研究[5-9]，Yu等[10]通过试验发现，随着腐蚀程度的增大，结构失效模式由因纵向钢筋屈服引起的弯曲破坏转变为由于横向钢筋断裂引起的弯剪破坏.Inci[11]采用非线性静力研究方法和非线性时间历程分析方法分析不同锈蚀程度、钢筋分布和不同地震强度对钢筋混凝土框架结构抗震性能影响.

钢筋混凝土结构在锈蚀与地震作用下的动力响应，直接影响结构安全性和耐久性[12].Luisa等[13]指出钢筋混凝土构件承载能力和延性会随着钢筋的锈蚀率增大而减小，在某些情况下，也会导致结构从塑性破坏转变为脆性破坏，这种作用对结构尤其是地震区的结构分析很有意义，这些区域延性特征和实际形成机理都是安全评估中的关键问题.目前，对耐久性退化钢筋混凝土结构抗震性能的研究多考虑钢筋锈蚀或混凝土碳化单一因素的影响，且未考虑钢筋锈蚀后粘结滑移退化对抗震性能的影响，碳化对结构抗震性能的影响研究也不尽合理，新建钢筋混凝土结构抗震设计也未考虑使用年限内结构耐久性损伤后抗震性能的时变特征，既有钢筋混凝土结构可靠度评定时也应考虑既有耐久性损伤及后续耐久性损伤的演化.本文通过足尺锈蚀钢筋混凝土构件低周反复荷载试验,验证有限元模型的准确性，采用精细化有限元全过程分析方法,从混凝土碳化率和钢筋锈蚀率的角度，考虑混凝土碳化、钢筋锈蚀及其引起的粘结滑移性能退化等多因素耦合作用，研究一般大气环境下使用年限内，耐久性退化钢筋混凝土构件抗震性能时变特征.

1一般大气环境下混凝土碳化及钢筋锈蚀时变特征

一般大气环境下，考虑CO2浓度、施工工艺、环境湿度和混凝土强度等影响因素，混凝土碳化深度的估算公式为：

(1)

k=3Kco2Kk1KktKksKFT1/4RH1.5(1-RH)×

(2)

(3)

KF=1.0+13.34F0.3.

(4)

式中：xc为混凝土的碳化深度(mm)；k为碳化系数；t为碳化时间(a)；fcuk为混凝土抗压强度(MPa)；Kco2,Kk1,Kkt,Kks和KF分别为CO2浓度影响系数、位置影响系数、养护浇筑影响系数、工作应力影响系数和粉煤灰取代系数；T，RH，C0，F分别为混凝土温度(℃)、环境相对湿度、CO2浓度(%)和粉煤灰重量比.

一般大气环境下钢筋开始锈蚀时间、锈胀开裂时间、临界锈蚀深度及钢筋锈蚀速率可根据文献[14]估算.钢筋开始锈蚀时间ti可按式(5)估算：

ti=[(c-x0)/k]2.

(5)

式中：c为保护层厚度(mm)．Dc为与保护层厚度及碳化系数有关的参数；m为局部环境系数；x0为碳化残量(mm)，按式(6)估算：

(6)

混凝土保护层锈胀开裂时间tcr为：

tcr=ti+δcr/λ0.

(7)

式中：λ0为保护层锈胀开裂时的年平均钢筋锈蚀速率(mm/a)；δcr为保护层锈胀开裂时的临界钢筋锈蚀深度(mm)，可按式(8)计算：

δcr=0.012c/d+0.000 84fcuk+0.018．

(8)

式中：d为钢筋直径(mm).

保护层锈胀开裂时的年平均钢筋锈蚀速率λ0按式(9)估算：

λ0=7.53kclm(0.75+0.012 5T)×

(9)

式中：kcl为钢筋位置影响系数；T,RH分别为年平均温度和年平均相对湿度.

保护层锈胀开裂后年平均钢筋锈蚀速率λ1为：

λ1=(4.5-340λ0)λ0.

(10)

以湖南长沙人群密集的民用建筑为例，以试验构件为例，经计算，箍筋开始锈蚀时间为14.4 a，纵筋开始锈蚀时间为22.4 a.混凝土碳化及钢筋锈蚀时变特征见图1.

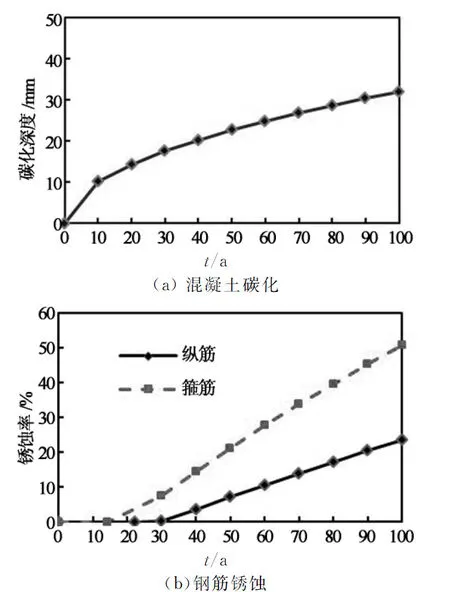
图1　一般大气环境下耐久性的时变特征

2钢筋混凝土构件抗震性能时变特征有限元模型

2.1有限元分析模型

采用ABAQUS有限元软件进行建模并对试件进行模拟计算.混凝土选取塑性损伤本构模型，采用C3D8R单元，钢筋采用T3D2单元.钢筋与混凝土联结采用SPRING2弹簧单元，如图2所示.弹簧单元1约束钢筋单元节点与混凝土单元节点的水平位移，弹簧刚度由能量等值原理确定；弹簧单元2约束钢筋单元节点与箍筋内部混凝土单元节点的竖直位移，弹簧刚度取极大值.

图2　钢筋混凝土联结单元

联结单元弹簧刚度的确定方法:能量等值法如图3所示，根据文献[15]中锈蚀钢筋混凝土粘结滑移本构关系，使得SOABCD=SDEFG，其中，残余段F点滑移值取下降段CG延长线与滑移量坐标轴交点H的滑移值，从而确定弹簧刚度K.

图3　联结单元弹簧刚度

为模拟箍筋对混凝土约束作用，将保护层与内侧混凝土分开建模，并选取不同的本构关系，考虑到荷载作用下箍筋外侧混凝土压碎后剥落，不再承受荷载，而箍筋内部混凝土由于受到约束作用局部压碎后仍可参与后续受力，故在建立混凝土本构关系时考虑箍筋的约束，将混凝土分为核心混凝土和非核心混凝土，核心混凝土考虑横向约束作用对混凝土强度的提高.一般大气环境下混凝土碳化深度通常未达到核心混凝土区域或对核心混凝土区域影响较小，故考虑碳化对混凝土本构关系的影响时，只考虑碳化对保护层非核心区域的影响.考虑到箍筋约束对混凝土受压力学性能的影响，根据研究成果[16]，引入配箍特征值进行修正.

图4　混凝土碳化率

2.2耐久性劣化材料本构关系

根据第2节计算结构使用年限分别为0，30，50，70和100 a时,钢筋混凝土构件保护层碳化深度分别为0，17.5，22.6，26.8和32 mm，相应地保护层碳化率分别为0，61%，77%，90%和100%.箍筋内侧混凝土考虑箍筋约束作用对混凝土本构关系的影响，箍筋外侧混凝土仅考虑碳化对本构关系的影响，本构关系采用作者建立的重复荷载下碳化混凝土本构关系模型[15]，见图5.碳化对混凝土抗拉强度的影响，在目前研究成果中未见报道，为此本文假设碳化不影响混凝土抗拉强度.

使用年限分别为0，30，50，70及100 a时，箍筋锈蚀率分别为0，7.43%，21.16%，33.79%和50.66%；纵筋锈蚀率分别为0，0.1%，7.15%，13.94%和23.64%.由于箍筋保护层厚度小于纵筋保护层厚度且直径较小，箍筋锈蚀速率大于纵筋锈蚀速率，约为纵筋锈蚀速率2倍.本构关系采用文献[17]建立的反复荷载下锈蚀钢筋本构关系模型.

2.3试验验证

试验试件共6个，设计图见图6.各试件设计锈蚀率分别为0，3%，6%，9%，12%和15%，锈蚀试验及测试方法依据GB/T50082-2009《普通混凝土长期性能和耐久性试验方法标准》进行,实测试件L-1，L-2，L-3，L-4，L-5，L-6锈蚀率分别为0，2.76%，5.47%，8.63%，9.81%和11.59%.混凝土设计等级为C30，实测立方体抗压强度为31.4 MPa，试件中纵筋采用HRB335，直径16 mm，对称配置，箍筋采用HPB300,直径8 mm，间距100 mm.

图5　碳化混凝土应力-应变曲线

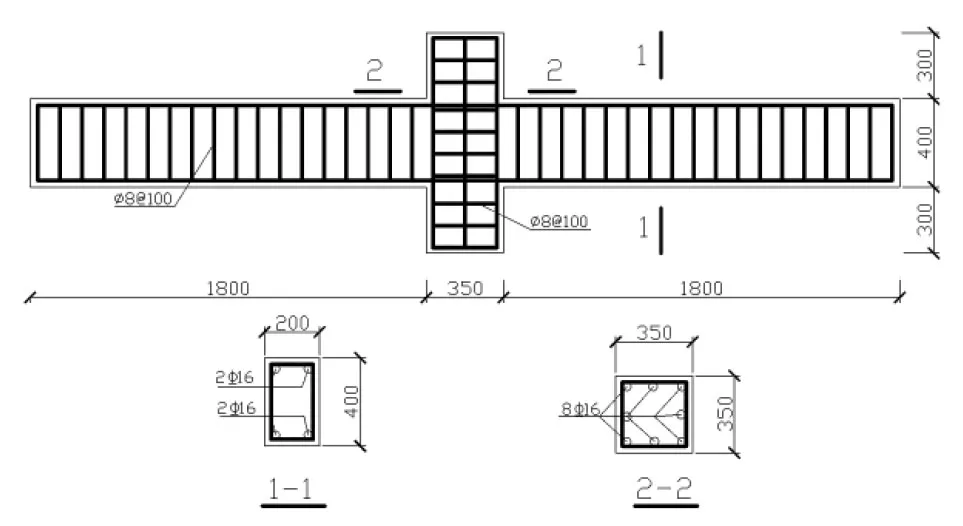
图6　试件设计(单位：mm)

试验装置采用MTS电液伺服试验机，按受弯构件加载，加载装置见图7.

试件两端部铰接，中部施加竖直反复荷载.加载时首先采用荷载控制循环加载直至试件进入屈服状态，屈服后改用位移控制，荷载控制的初始荷载取计算开裂荷载的50%，位移控制循环等级均为试验屈服位移Δy，每级循环3次，直至试件发生破坏，加载机制见图8.

图7　试验装置

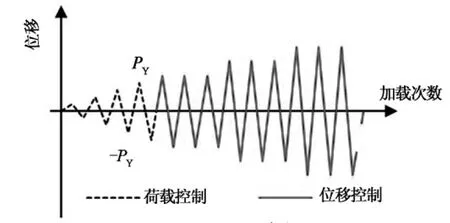
图8　试验加载机制

详细试验成果可参见文献[15]，取试件中部一侧进行有限元分析.箍筋外侧混凝土压碎时剥落，不考虑其受压恢复性能，但内侧混凝土压碎后，由于箍筋约束作用而不至剥落，内侧混凝土受压可以恢复.

以试件L-1及L-5为例，有限元模型计算结果与试验对比见图9及图10.

通过对比分析可知，分析结果与试验结果基本吻合，但有限元模拟滞回曲线更加饱满，再加载刚度初期偏大而后期偏小.这一方面是由于有限元计算中参数选取的复杂性，有限元参数选取的误差及试验中的误差都可能导致二者结果存在差异；另一方面，虽然本文采用弹簧单元模拟钢筋与混凝土的粘结滑移性能，但简化方法与真实情况有所差异.实际构件加载过程中，钢筋与混凝土的粘结强度随滑移量的增大而增大，达到极限粘结强度后，随滑移量的增大而减小，有限元模拟中采用能量法简化为刚度不变的弹簧单元，未能很好模拟再加载初期粘结滑移滞回曲线的平滑段，即宏观上表现为构件滞回曲线的捏拢效应，有限元计算曲线不如试验曲线明显.有限元计算的滞回曲线与试验曲线总体上接近，卸载路径及骨架曲线与试验吻合较好.对于工程应用中的弹塑性分析，这样的分析结果已经能够满足要求.本文所述的有限元计算方法对于模拟锈蚀钢筋混凝土构件在低周反复荷载作用下的响应有一定的准确性和可参考性，可以利用此法进行耐久性退化钢筋混凝土构件的抗震性能参数分析和退化规律分析.

图9　试件滞回曲线对比

图10　试件骨架曲线对比

3锈蚀钢筋混凝土构件抗震性能时变特征分析

3.1承载力及刚度退化分析

随着使用年限的增长，各试件滞回曲线见图11.

由图11可知，随着构件使用时间的增长，滞回环面积减小，饱满程度降低，达到峰值荷载后承载力及刚度退化愈加明显.各构件骨架曲线见图12.由图12可知，构件使用年限在30 a内骨架曲线变化不大，使用时间对构件刚度及承载力影响较小；当使用年限超过30 a后，骨架曲线变化较大，由于钢筋锈蚀，构件刚度及承载力发生显著退化.

图11　使用年限内构件滞回曲线

Δ/mm

随着使用时间的延长，骨架曲线达到峰值荷载后平直段明显变短，延性降低.使用年限内各构件力学性能及滞回性能见表1.

各构件承载力衰减曲线见图13.对承载力退化比计算值分析可知，承载力随使用年限的增长，在30 a之前和30 a之后的退化速率明显不同，退化规律采用分段式表示，见式(11).

使用年限/a

(11)

式中：FE,T为构件承载力退化比；T为使用年限(a).

由图13及式(11)可知，构件承载力在使用30 a内承载力变化较小，之后随使用年限的增长退化速率增大，当使用100 a时，承载力降低22.5%.

各构件割线刚度随位移变化衰减曲线见图14.

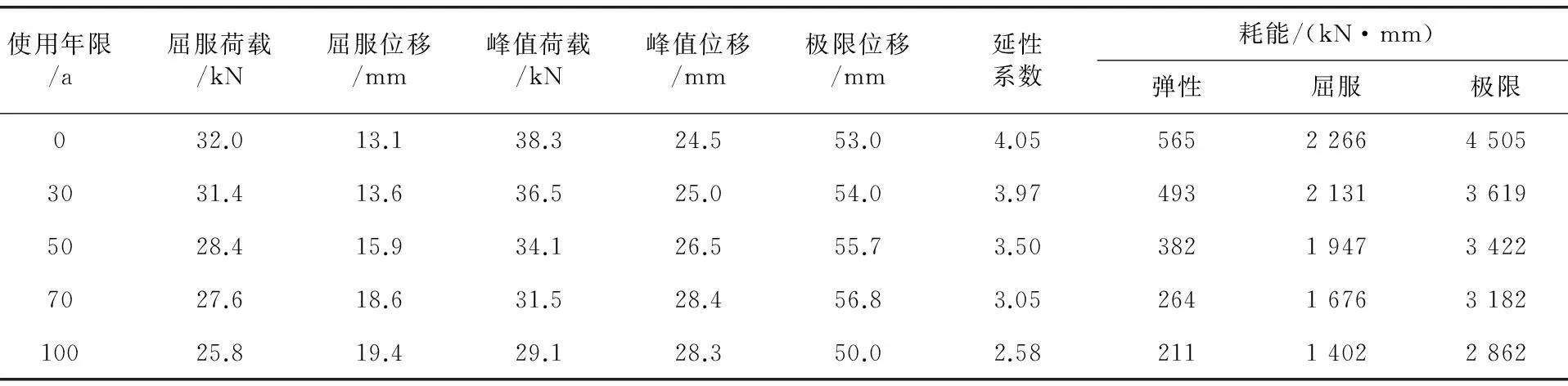
表1　使用年限内构件性能

位移/mm

以峰值状态为例，其割线刚度随使用年限的增长变化趋势见图15.

对刚度退化比计算值分析，可知刚度随使用年限延长，退化规律见式(12).

(12)

式中：KE,T为构件刚度退化比.

使用年限/a

由以上分析可知：构件屈服前，刚度随着变形增加迅速降低，屈服后，刚度下降速度减慢，当变形达到峰值位移后，刚度趋于平稳；随着使用年限的增长，刚度退化在构件从屈服至峰值状态时更为明显，达到峰值状态后，构件退化速率基本一致；另一方面，各构件刚度随使用年限的增长，30 a内退化速率较小，30 a后刚度退化速率逐渐增大，当使用100 a时，刚度约退化33.5%.

3.2滞回性能退化分析

各构件滞回性能见表1，其中弹性状态耗能取最大位移为10 mm时滞回环面积，屈服耗能取屈服位移滞回环面积，极限耗能取极限状态下滞回环面积.

使用年限内各构件延性及极限耗能性能随时间的变化见图16.

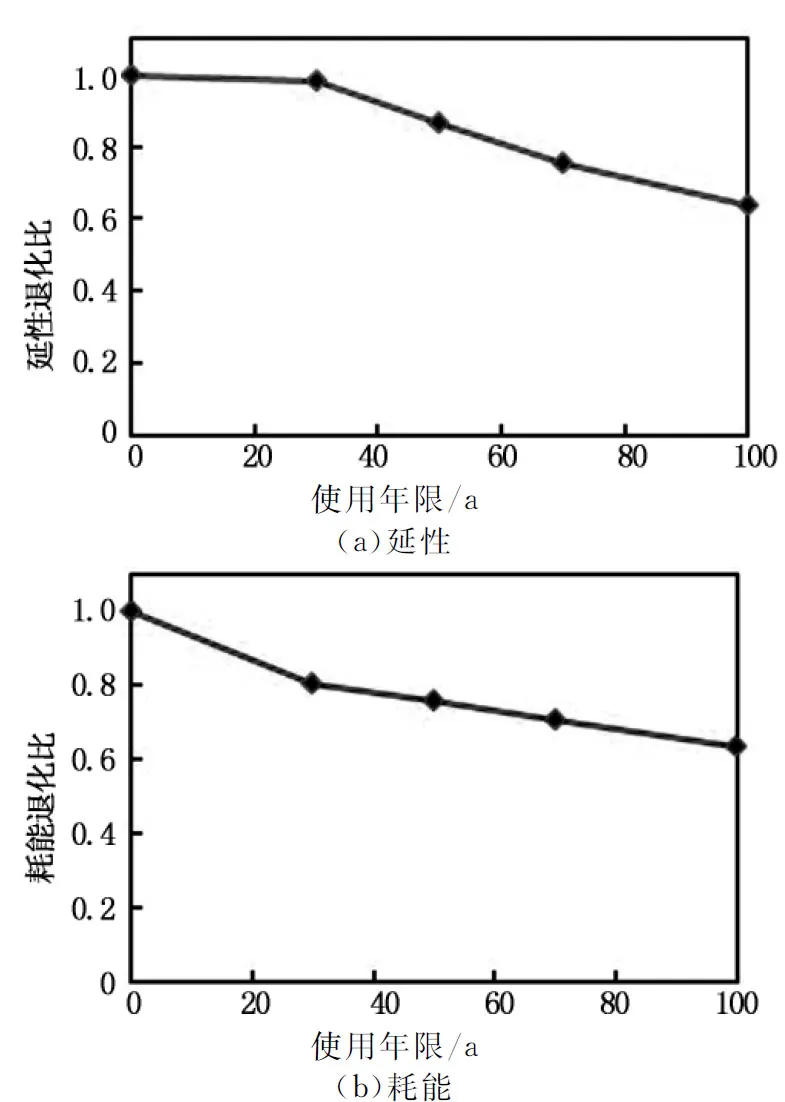
图16　构件滞回性能退化曲线

对延性及耗能退化比计算值分析，可知延性及耗能随使用年限延长，退化规律分别见式(13)及式(14).

(13)

(14)

式中：μE,T为构件延性退化比；EE,T为构件耗能退化比.

由图16及式(13)，(14)可知，钢筋混凝土构件随着使用年限的增长，延性及耗能性能降低，当使用年限为100 a时，延性降低36.7%，耗能能力降低40.5%，耗能退化相对较为严重.另一方面，锈蚀可能导致结构破坏模式的转变，文献[18]根据试验，并考虑坑蚀的影响，并将锈蚀转化为服役年限，其试验构件承载力随时间变化见图17.

使用年限/a

由图17可知，若构件在使用年限内出现较为严重的坑蚀，则可能导致构件抗弯强度大于抗剪强度，构件首先达到其抗剪强度，在破坏模式转换点之后，构件发生剪切破坏，从而可能导致结构在地震中发生脆性破坏，甚至突然倒塌.

综合考虑一般大气环境下钢筋混凝土构件抗震性能的演化规律，建议在一般大气环境下钢筋混凝土构件抗震设计时，应考虑典型环境中构件随使用年限增长导致抗震性能的退化，从而保证结构良好的抗震性能.

4结论

本文通过对一般大气环境下耐久性退化钢筋混凝土受弯构件抗震性能演化规律的分析，主要结论如下：

1)随着钢筋锈蚀程度的增大，试件承载力、刚度及耗能性能逐渐降低.钢筋锈蚀导致其屈服点逐渐消失，使得构件屈服弯矩与极限弯矩接近，屈服区长度变短，构件延性降低.

2)一般大气环境下，混凝土碳化率随使用年限增长逐渐增大，但碳化速率逐渐减小.钢筋锈蚀开始后，其锈蚀率随时间基本呈线性关系，随使用年限增长，锈蚀程度逐渐增大，箍筋锈蚀速率大于纵筋锈蚀速率，约为其2倍.

3)一般大气环境下，钢筋混凝土受弯构件使用年限在30 a内，构件抗震性能变化不大；当使用年限超过30 a后，构件刚度、承载力及滞回性能发生显著退化.当使用100 a时，一般大气环境下承载力降低22.5%，刚度约退化33.5%，延性降低36.7%，耗能能力降低40.5%.

4)根据计算分析，给出了一般大气环境下使用年限内，受弯构件承载力、刚度、延性及耗能性能退化规律计算式.综合考虑一般大气环境钢筋混凝土构件抗震性能的演化规律，建议对钢筋混凝土构件抗震设计时，应考虑典型环境中构件随使用年限增长导致抗震性能的退化，从而保证结构良好的抗震性能，防止突然倒塌.

参考文献

[1]CAIMAS J, PLIZZARI G A, DU Y G.etal.Mechanical properties of corrosion damaged reinforcement[J]. ACI Materials Journal,2005,102(4):256-264.

[2]徐有邻.混凝土结构设计原理及修订规范的应用[M] .北京:清华大学出版社，2012：1-10．

XU You-lin. Application of design principle of concrete structure and revised norms[M]. Beijing：Tsinghua University Press，2012：1-10.(In Chinese)

[3]梁岩，罗小勇．耐久性损伤钢筋混凝土结构抗震性能研究进展[J].地震工程与工程振动，2014，34(2)：113-119．

LIANG Yan，LUO Xiao-yong. Research progress in seismic behavior of durability decrease RC structures[J].Earthquake Engineering and Engineering Vibration,2014,34(2):113- 119．(In Chinese)

[4]KYIOSHI O, KAZUO K，TOYOAKI M. Influence of longitudinal cracking due to reinforcement corrosion on characteristics of reinforced concrete members[J]. ACI Structural Journal，1988，85(2):134-140.

[5]WILKINS A，NEIL M H．Seismic retrofitting of corroded reinforced concrete columns using carbon composites [J]．ACI Structural Journal，2007，104(3)：348-356．

[6]SUH K，MULLINS G．Effectiveness of fiber-reinforced polymer in reducing corrosion in marine environment [J]．ACI Structural Journal，2007，104(1)：76-83．

[7]陈新孝，牛荻涛，王学民．锈蚀钢筋混凝土压弯构件的恢复力模型[J].西安建筑科技大学学报，2005，37(2)：155-159．

CHEN Xin-xiao, NIU Di-tao, WANG Xue-min. The force-restoring model of corroded reinforced concrete members with flexure and compression[J]. Xi’an University of Architecture and Technology Journal, 2005,37(2):155-159.(In Chinese)

[8]贡金鑫，李金波，赵国藩．受锈蚀钢筋混凝土构件的恢复力模型[J].土木工程学报，2005，38(11)：38-44.

GONG Jin-xin, LI Jin-bo, ZHAO Guo-fan. Restoring force model of corroded reinforced concrete elements[J]. China Civil Engineering Journal,2005,38(11):38-44.(In Chinese)

[9]梁岩，罗小勇, 陈代海.锈蚀钢筋混凝土构件基于地震损伤的恢复力模型研究[J]. 振动与冲击, 2015, 34(5): 199-206.

LIANG Yan，LUO Xiao-yong，CHEN Dai-hai.Research on restoring force model of corroded reinforced concrete members based on seismic damage[J]. Journal of Vibration and Shock, 2015, 34(5): 199-206.(In Chinese)

[10]YU C O，LI L T，HOU H C. Cyclic performance of large-scale corroded reinforced concrete beams[J]. Earthquake Engineering and Structural Dynamics,2012，41:593-604.

[11]INCI P. Effects of reinforcement corrosion on the performance of RC frame buildings subjected to seismic actions[J]. Journal of Performance of Constructed Facilities, 2014, 27(6):683-696.

[12]TIEJUN L, JILONG L, JINPING O. High damping concrete and seismic behavior[C]//Third International Conference on Construction Materials. Vancouver:Department of Civil Engineering the University of British Columbia, 2005:365 -373.

[13]LUISA B, RENATO V, ANNA S,etal.Seismic assessment of existing RC structures affected by degradation phenomena [J].Structual Safety, 2009,31 (4):284-297.

[14]CECS220-2007混凝土结构耐久性评定标准[S].北京：中国建筑工业出版社，2007:34-36.

CECS220-2007Concrete structure durability evaluation code[S]．Beijing: China Architecture Building Press，2007:34-36.(In Chinese)

[15]梁岩.耐久性退化钢筋混凝土构件抗震性能及设计方法研究[D].长沙：中南大学土木工程学院，2014:21-76.

LIANG Yan. Study on seismic performance and design method of durability deteriorated reinforced concrete member[D].Changsha：College of Civil Engineering,Central South University，2014:21-76.(In Chinese)

[16]钱稼茹，程丽荣，周栋梁.普通箍筋约束混凝土柱的中心受压性能[J].清华大学学报:自然科学版,2002,42(10): 1369-1373.

QIAN Jia-ru,CHENG Li-rong,ZHOU Dong-liang. Behavior of axially loaded concrete columns confined with ordinary hoops[J]. J Tsinghua Univ:Sci & Technol,2002, 42(10):1369-1373.(In Chinese)

[17]罗小勇，梁岩，张艳芳. 重复拉伸荷载下锈蚀钢筋力学性能及本构关系研究 [J].湖南大学学报:自然科学版，2014，41(11)：81-86.

LUO Xiao-yong, LIANG Yan, ZHANG Yan-fang. Study on mechanical property and constitutive relation of corroded steel bars under tension cyclic loading [J]. Journal of Hunan University:Natural Sciences,2014,41(11):81-86.(In Chinese)

[18]蔡立伦．含腐蚀钢筋之钢筋混凝土梁耐震行为[D]．台湾：国立台湾科技大学营建工程系，2011:115-121.

CAI Li-lun.Seismic beavior of reinforced concrete beams with corroded steel reinforcement[D].Taiwan:Department of Civil and Construction Engineering, The National Taiwan University of Science and Technology,2011:115- 121.(In Chinese)

Time-dependent Seismic Performance of Reinforced Concrete Member under Common Atmosphere Environment

LIANG Yan1†,CHEN Huai1,LUO Xiao-yong2

(1.College of Civil Engineering, Zhengzhou Univ, Zhengzhou,Henan450001,China;2.College of Civil Engineering, Central South Univ, Changsha,Hunan410075,China)

Abstract:Based on high-precision nonlinear finite element analysis, the multi-factor combined effects on reinforced concrete were considered, including concrete carbonation, reinforcement corrosion, and bond-slip performance degradation. And a refined finite element model was established to investigate the influence of durability deterioration on the seismic performance of reinforced concrete members in common atmosphere environment from corrosion rate of reinforcement and carbonation rate of concrete. It is revealed that ,when the service life was less than 30 years, the seismic performance of reinforced concrete members was changed little, while after 30 years, it degraded significantly. On the other hand, when the service life reached 100 years, concrete bearing capacity decreased to 22.5 %, stiffness decreased to 33.5 %, ductility decreased to 36.7 % and energy dissipation decreased to 40.5 %. To this end, it suggests that the influence of the service life and durability deterioration on seismic performance of the reinforced concrete members in common atmosphere environment should be considered in seismic design to guarantee the earthquake-resisting capacity of the structures.

Key words:reinforced concrete; durability; anti-seismic; time dependent; common atmosphere environment

中图分类号：TU375

文献标识码：A

作者简介：梁岩(1986-)，男，河南洛阳人，郑州大学讲师，博士†通讯联系人，E-mail:lyfeel555@163.com

基金项目：国家自然科学基金资助项目(51178470)，National Natural Science Foundation of China(51178470)；国家自然科学基金重点资助项目(U1361204)，Major Research Project of National Natural Science Foundation of China(U1361204)

*收稿日期：2015-05-14

文章编号：1674-2974(2016)03-0104-09