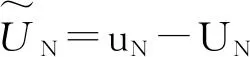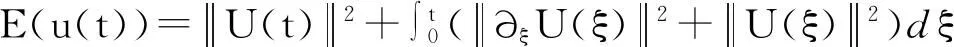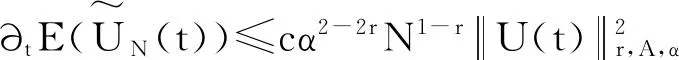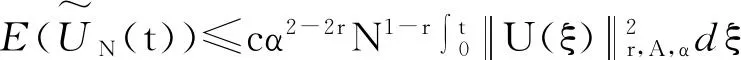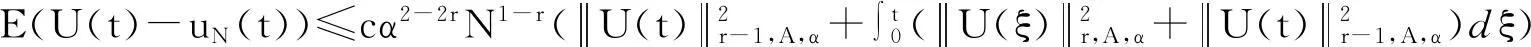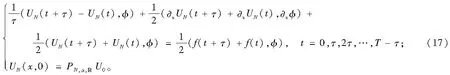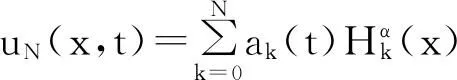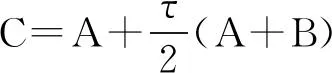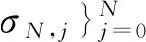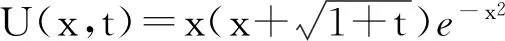全直线上热传导方程广义Hermite 谱方法

张　琼，王天军

(河南科技大学 数学与统计学院,河南 洛阳 471023)



全直线上热传导方程广义Hermite 谱方法

张琼，王天军

(河南科技大学 数学与统计学院,河南 洛阳 471023)

摘要：以带伸缩因子的广义Hermite函数为基函数展开全直线上热传导方程的数值解，逼近热传导方程的正确解。给出算法格式和收敛性分析，数值例子表明所提算法格式具有有效性和高精度。所用方法也可用于求解其他同类问题。

关键词：热传导方程；初值问题；广义Hermite谱方法；全直线

0引言

过去30年来,利用谱方法数值求解无界区域上的偏微分方程的研究有了很大进展[1-5]，该方法的主要优点是高精度和无需强加人工边界条件。文献[1-2]考虑了权函数为e-x2的Hermite多项式作为基函数的逼近问题。文献[3]考虑了权函数为ex2的Hermite函数作为基函数的逼近问题。但上述文献中许多工作所用权函数都是非一致的,使理论分析和数值计算更加复杂。所以,文献[4-6]利用权函数为1的Hermite函数作为基函数的逼近方法。为了提高逼近精度，文献[7-9]考虑了带伸缩因子的广义Hermite函数作为基函数来逼近[7-9]，值得关注的是，文献[8]将该基函数用于求解关于种群问题的Ginzburg-Landau方程的数值解。文献[10]用Legendre谱配置方法求解热传导问题的数值解。但关于无界区域上热传导问题的高精度方法的研究较少。本文利用带伸缩因子的广义Hermite函数求解全直线上热传导方程的数值解，通过选取适当伸缩因子，可以更好地使数值解匹配正确解的渐进行为，达到提高数值逼近精度的目的。

1广义Hermite 正交逼近

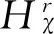
令Hn(x)为通常的Hermite多项式,广义Hermite函数定义为:

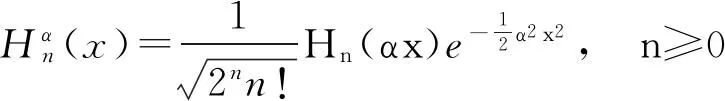
其中：α是一个常数，且α>0。

∫,

(1)

其中:δm,n为Kronecker函数。

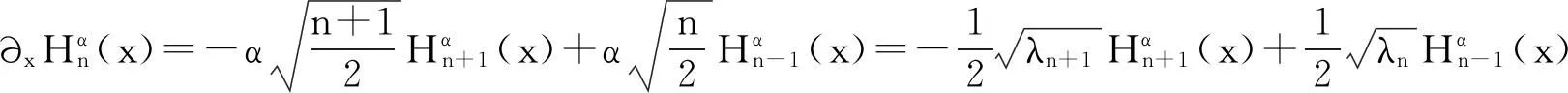
(2)

∫；

(3)

∫；

(4)

∫,当n≠m,n≠m±2。

(5)

对于整数N>0,PN()表示次数小于等于N的所有多项式，令

为了得到逼近结果，需要引进下面的范数空间。对于任意的整数r≥0,

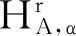
L2()正交投影记为PN,α,:L2()→QN,α()，定义：

(PN,α,Ru-u,φ)=0,φ∈QN,α()。

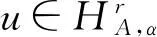
(6)

其中：常数c与任意函数以及N无关。

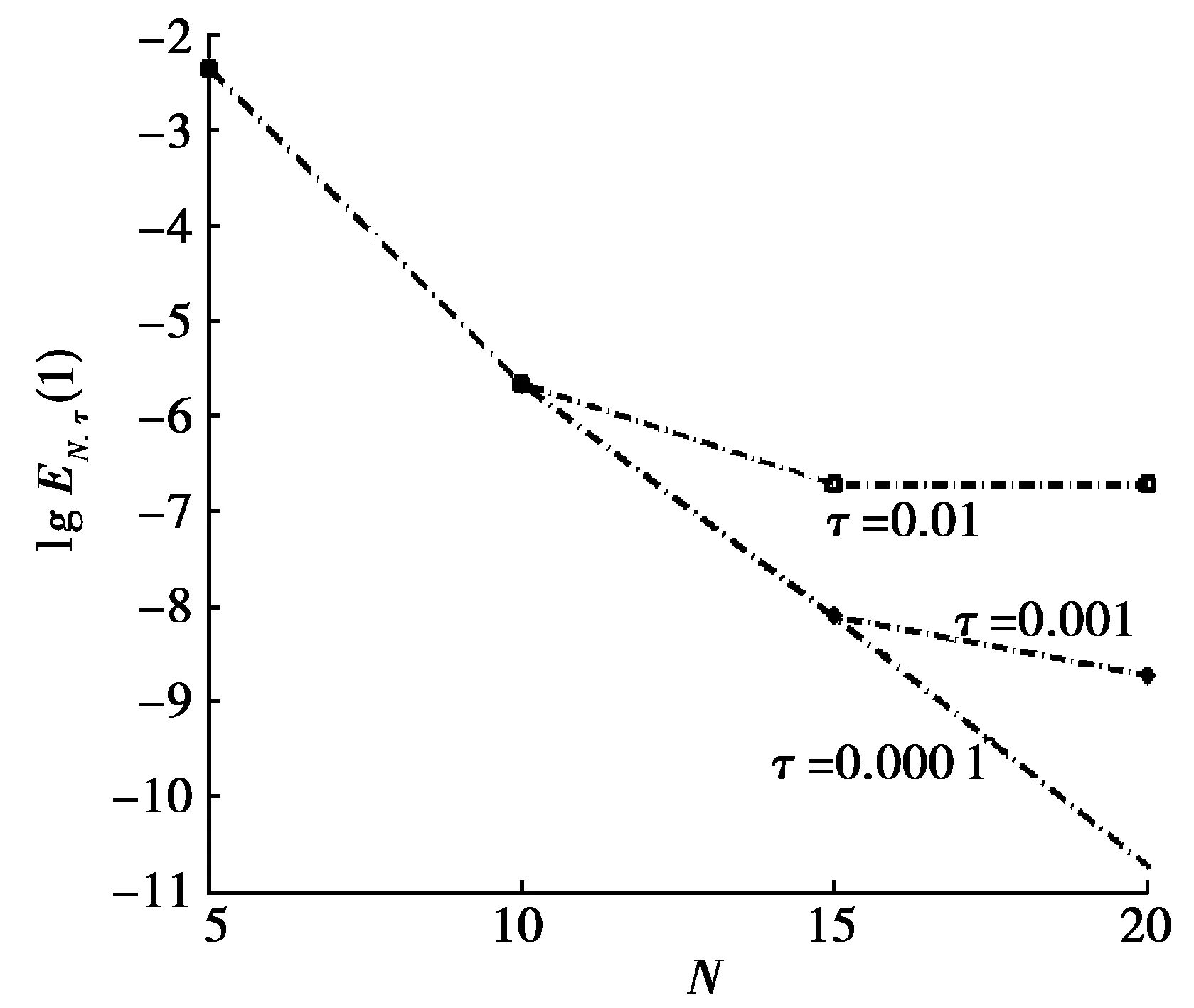
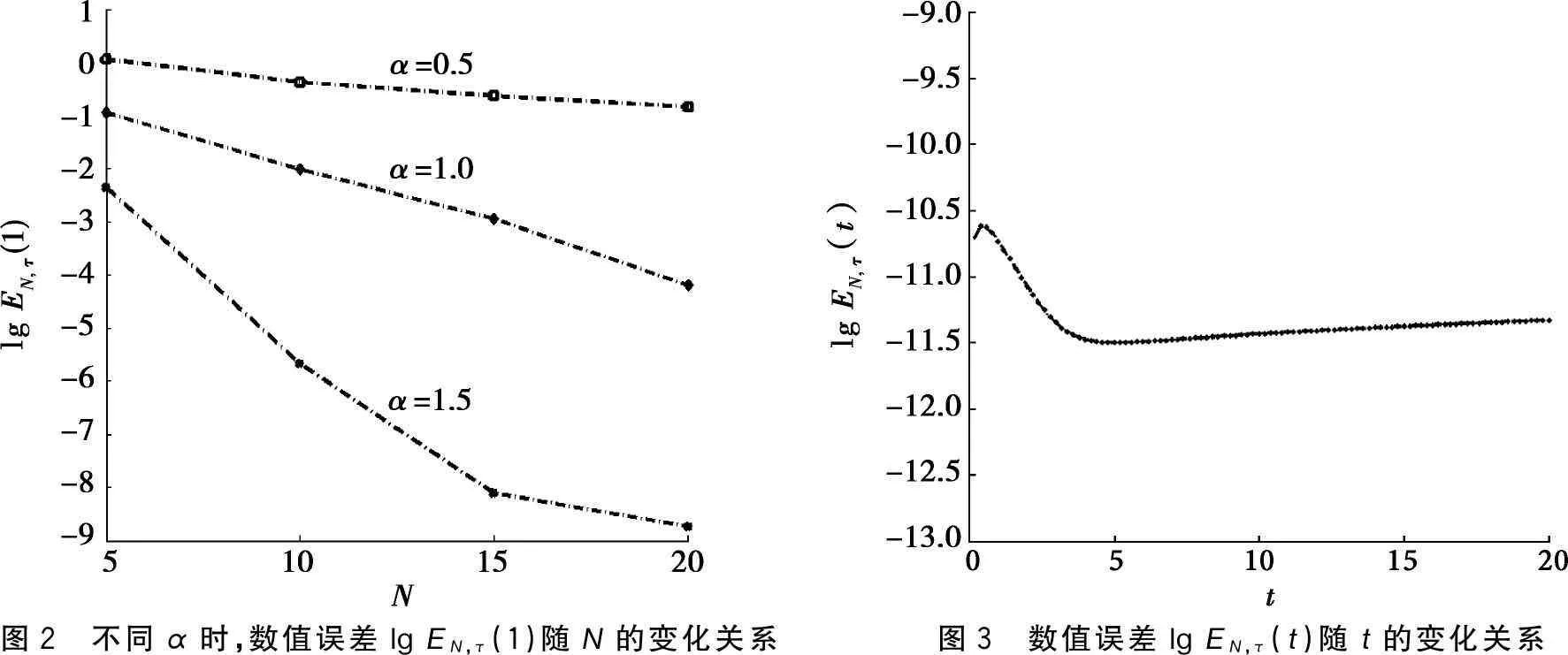
2全直线上线性热传导方程的广义Hermite谱方法

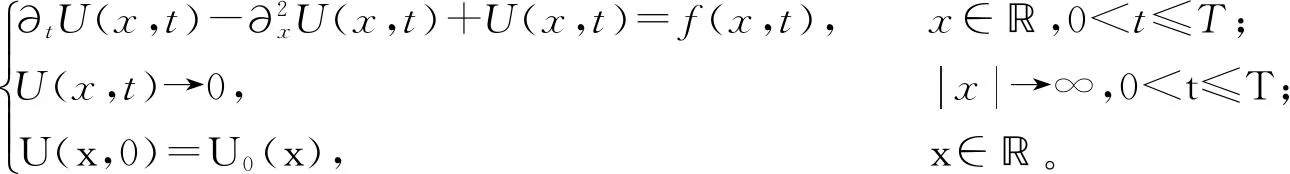
tU(x,t)-2xU(x,t)+U(x,t)=f(x,t), x∈ℝ,0

(7)

式(7)的一个弱形式为求U∈L∞(0,T;L2())∩L2(0,T;H1()),使得：

(8)

式(8)的谱格式为求uN∈QN,α(),使得：

(9)

现在分析式(9)的收敛性。令UN=PN,α,U,再由式(8)和PN,α,的定义,可以得到：

(10)

(11)

(12)

为了简便，令

(13)

则式(12)为：

(14)

(15)

由式(6)、式(13)和式(15)得：

(16)

3数值结果

对时间方向用Crank-Nicolson格式离散，其步长为τ，得到全离散格式为：

在实际的计算中，将数值解展开成如下形式:

(18)

定义向量

X(t)=(a0(t),a1(t),…,aN(t))T；F(t)=(f0(t),f1(t),…,fN(t))T,

(19)

由式(1)、式(3)、式(4)和式(5)可知：

ak'k=πα, k'=k;0,k'≠k,ìîíïïïï bk'k=-α2πk(k-1), k'=k-2, 0≤k,k'≤N。πα(k+12),k'=k,0≤k,k'≤N。-α2π(k+1)(k+2),k'=k+2,0≤k,k'≤N。0,k'≠k,k±2,0≤k,k'≤N。ìîíïïïïïïïïïï

用离散内积

来度量问题的正确解U(x,t)和数值解uN(x,t)之间的误差。现在令测试函数：

可得数值误差EN,τ(t)的常用对数和不同N之间的关系。

图1　不同τ时，数值误差lg EN,τ(1)随N的变化关系

图1为时间t=1，基函数中的松弛因子α=1.5时，数值误差的常用对数lgEN,τ(t)随多项式次数N及时间步长τ的变化情况。由图1可看出：固定τ=0.01，当N≤15时，影响误差的主要因素是空间变量，数值误差EN,τ(t)随着多项式次数N的增大而快速减小;但当N>15时，影响误差的主要因素是时间变量，随着N的变大，数值误差EN,τ(t)基本保持不变。当τ=0.001时，情况类似。然而，对于τ=0.000 1，影响数值误差的主要因素是空间变量，所以随着N的增大，数值误差EN,τ(t)迅速减小。这种情况和式(16)所给的数值误差分析结果是一致的，而且可以很好地表明式(9)在空间方向上具有谱精度。

图2为时间t=1，时间步长τ=0.001时，数值误差的常用对数lgEN,τ(t)和基函数中的伸缩因子 α之间的关系。图2表明：当 α取适当大的值时所得的数值误差,比 α取值小时所得的数值误差更小些。但如何选取最恰当的 α值，还是一个未解决的问题，有待继续研究。

图3为伸缩因子 α=1.5, 多项式次数N=20，时间步长τ=0.000 1时，lgEN,τ(t)随t的变化关系。图3表明式(9)具有长时间稳定性。

图2 不同α时,数值误差lgEN,τ(1)随N的变化关系 图3 数值误差lgEN,τ(t)随t的变化关系

4结束语

利用广义Hermite基函数展开数值解，逼近全直线上的热传导问题的正确解，由于基函数含有因子e-(αx)2/2，使得数值解能更好地吻合正确解在无穷远处的渐进行为。适当选取函数e-(αx)2/2中的伸缩因子α，使得数值解更好地逼近正确解。由于算法格式中所含权函数是一致的，给理论分析和数值计算带来了方便，在计算中可以节省大量工作。本文所提的计算方法也可用于求解全直线上非线性问题的数值解。

参考文献：

[1]GUO B Y,XU C L.Hermite pseudospectral method for nonlinear partial differential equations[J].ESAIM:mathematical modelling and numerical analysis,2000,34(4):859-872.

[2]GUO B Y.Error estimation of hermite spectral method for nonlinear partial differential equations[J].Mathematics of computation of the American mathematical society,1999,68(227):1067-1078.

[3]GUO B Y,WANG T J.Mixed legendre-hermite spectral method for heat transfer in an infinite plate[J].Computers & mathematics with applications,2006,51(5):751-768.

[4]GUO B Y,SHEN J,XU C L.Spectral and pseudospectral approximations using hermite functions:application to the dirac equation[J].Advances in computational mathematics,2003,19(1/3):35-55.

[5]SHEN J,TANG T,WANG L L.Spectral methods:algorithms,analysis and applications[M].Berlin:Springer Science & Business Media,2011.

[6]黄瑜,徐承龙.无界域上一类半线性波动方程的全离散谱格式[J].同济大学学报(自然科学版),2012,40(4):635-639.

[7]TANG T.The hermite spectral method for gaussian-type functions[J].SIAM journal on scientific computing,1993,14(3):594-606.

[8]XIANG X M,WANG Z Q.Generalized hermite spectral method and its applications to problems in unbounded domains[J].SIAM journal on numerical analysis,2010,48(4):1231-1253.

[9]ZHANG C,GUO B Y.Generalized hermite spectral method matching asymptotic behaviors[J].Journal of computational and applied mathematics,2014,255:616-634.

[10]王天军,贾丽蕊.非线性热传导方程的 Lagrange 插值逼近[J].河南科技大学学报(自然科学版),2011,32(2):68-71.

中图分类号：O175.2

文献标志码：A

收稿日期：2015-01-23

作者简介：张琼(1987-),女,河南巩义人,硕士生;王天军(1963-),男,通信作者，河南息县人,副教授,博士,硕士生导师,主要研究方向为偏微分方程数值解.

基金项目：国家自然科学基金项目(11371123，11171227);河南省教育厅自然科学基金项目(14B11021);河南科技大学博士启动基金项目(09001263)

文章编号：1672-6871(2016)03-0091-04

DOI:10.15926/j.cnki.issn1672-6871.2016.03.020