一类四次Kolmogorov系统的极限环分支

吴岱芩,黄文韬，2 ,吴燕兰

(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004；2.贺州学院 数学系,广西 贺州 542800)



一类四次Kolmogorov系统的极限环分支

吴岱芩1,黄文韬1，2,吴燕兰1

(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004；2.贺州学院 数学系,广西 贺州 542800)

摘要：研究了一类四次Kolmogorov系统在正平衡点(1,1)处的极限环分支问题。运用计算机代数系统Mathematica计算其伴随复系统的前5个奇点量，并给出正平衡点(1,1)成为五阶细焦点的条件，再利用雅克比行列式方法证明正平衡点(1,1)处可分支5个小振幅极限环。

关键词：Kolmogorov系统；正平衡点；极限环；奇点量

0引言

Kolmogorov系统被广泛运用于生态学，用来描述两种群之间相互作用的关系。对该系统动力学行为特别是极限环问题的研究越来越引起数学和生态学工作者的兴趣。文献[1]研究了一类三次Kolmogorov系统，得到三次Kolmogorov系统可分支出4个极限环的结论。文献[2]发现了一类三次Kolmogorov系统从1个正平衡点可分支出3个极限环。文献[3]也研究了一类三次Kolmogorov系统，得到6个极限环。文献[4]研究了三次Kolmogorov系统，得到5个极限环。文献[5]研究了一类具有2个正平衡点的三次Kolmogorov系统，得到可分支出6个极限环的结论。文献[6]把研究Kolmogorov系统极限环问题推广至三维系统。而四次Kolmogorov系统的小振幅极限环分支问题，因其偶数次系统在计算上的困难性，仅有文献[7]讨论了一类四次Kolmogorov系统3个正平衡点极限环问题。本文在文献[1-10]的基础上，研究如下四次Kolmogorov系统：

(1)

1基础知识

考虑一类多项式实系统:

(2)

其中：Xk(x,y),Yk(x,y)是关于x,y的k次齐次多项式。当δ=0时，系统(2)通过变换

(3)

化为复系统：

(4)

其中：

(5)

z,w,T,aα,β,bα,β均为复变量。

引理1对系统(4)，可逐项确定形式级数:

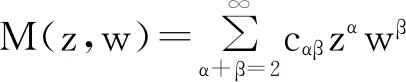
(6)

使得

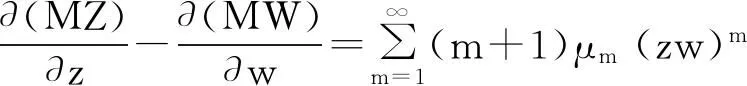
(7)

其中：当α=β=0时，即cαβ=c00，取c00=1；当α<0，或β<0，或α=β>0时，置cαβ=0，其他情形cαβ由递推公式

(8)

确定。对任意正整数m,μm由递推公式

(9)

确定。其中：μm为系统(4)的第m个奇点量[12]。

又由系统(2)的首个非零焦点量v2m+1(2π)与其伴随复系统的首个非零奇点量μm满足[13]：

v2m+1(2π)=iπμm，

(10)

因此，系统(2)焦点量的计算可以化为系统(4)奇点量的计算。

2伴随复系统的奇点量

系统(1)有正平衡点(1,1)，要讨论该点处极限环分支问题，作变换u=x-1,v=y-1，系统(1)化为如下系统：

(11)

如此，可研究系统(11)的焦点量与极限环分支情况。如果直接计算系统(11)的焦点量，比较复杂，可将实系统转化为对应的伴随复系统，用与焦点量等价的奇点量进行计算。作变换(3),系统(11)化为以下系统：

(12)

系统(12)称为系统(11)的伴随系统，其中：

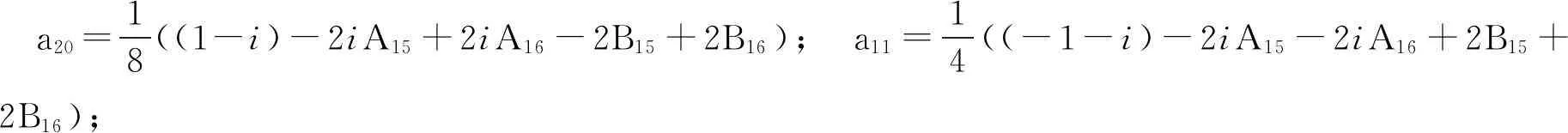
a20=18((1-i)-2iA15+2iA16-2B15+2B16); a11=14((-1-i)-2iA15-2iA16+2B15+2B16);

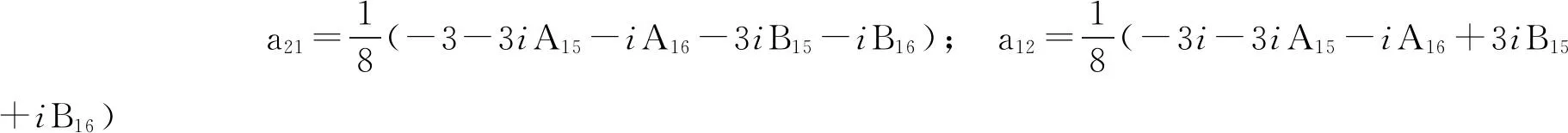
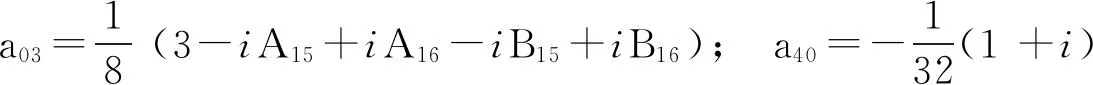
运用式(8)和式(9)，用计算机代数系统Mathematica进行计算和化简可得下面的定理。

定理1复系统(12)原点的前5个奇点量如下：

μ1=i4(-3A15-3B15-2A16B15+2A15B16); μ2=i24(A16+B16)F2

20B162r +20 A16B162r-66r2-46A16r2+4A162r2+46B16r2-32A16B16r2-

24A162B16r2+4B162r2+24A16B162r2-684r3-636A16r3-144A162r3+636B16r3+

496A16B16r3+80A162B16r3-144B162r3-80A16B162r3-648r4-648A16r4-

144A162r4+648B16r4+576A16B16r4+96A162B16r4-144B162r4-96A16B162r4；

上述表达式在计算μk时，已置μ1=μ2=…=μk-1=0,k=2,3,4,5。其中,F3、F4和F5也为A16、B16和r的表达式，其式较复杂，故在此省略。

由定理1可得下面的定理。

结果显示，患者的门诊自付费用受到就医医疗机构层次的显著正向影响(P<0.05)；对患者的住院自付费用产生显著正向影响的是：医疗机构的层次和住院天数。值得注意的是，中低收入水平的患者其年次均住院自付费用低于低收入组，分析住院服务利用时发现，低收入组对住院服务的实际利用大于中低收入组。经统计，低收入组患者因住院而借钱的比率为6%，中低收入组的比率为2%，中高收入组和高收入组分别为1.6%和0.6%，由此可见，低收入组患者通过负债(主要是向亲戚借钱)的筹资手段实现了更多的住院医疗服务需要。

定理2系统(12)原点的前五阶奇点量均为0，当且仅当A15=-B15,A16=-B16成立。

证明由定理1不难得到充分性成立，下面证明必要性。

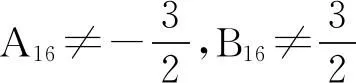
综上所述：μ1=μ2=μ3=μ4=μ5=0⟹A16=-B16,A15=-B15,必要性得证。

3系统的极限环分支

定理3当μ1=μ2=μ3=μ4=0,μ5≠0时，系统(12)的原点为五阶细奇点(对应的系统(11)的正平衡点(1,1)为五阶细焦点)的充分必要条件为：

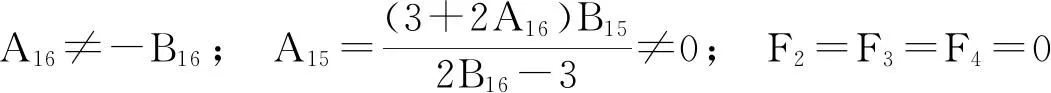
(13)

式(13)是系统(1)正平衡点成为五阶细焦点的条件，但这样形式的条件不便在极限环的分析中应用。下面，给出式(13)的一种具体形式。因为方程组F2=F3=F4=0的精确符号解过于复杂，故本文求其近似解。用Mathematica算符NSolve[{F2==0,F3==0,F4==0},{A16,B16,r},50]来求F2=F3=F4=0近似解，得到满足条件的多组解，取其中一组解为：

A16=-1.59982624221084548812576116452269676067;B16=-0.22655347077919503934714017334958132353;r= 0.95947681422643813797891234970925361665。ìîíïïïï

进而可得A15,A16,B15,B16的一组近似解为：

(14)

式(14)即为条件(13)的一种具体表示形式。

考虑到焦点量和奇点量的关系式(10)及文献[14]中的定理4.7，可得下面的定理。

定理4 对系统(2)，当δ=0时，伴随复系统原点的奇点量μi(i=1,2，…)有k个线性无关的参数θ=(θ1，θ2，…，θk)。当θ=θ0时，系统(3)的原点为n阶细奇点，若雅克比行列式满足

(15)

则系统(2)原点的充分小领域内存在n个小振幅极限环。

定理5当系数满足式(14)时，系统(11)正平衡点(1,1)为五阶细焦点，通过扰动，系统在正平衡点(1,1)处可分支出5个小振幅极限环。

证明由定理4，欲证明系统(1)在正平衡点邻域可分支出5个极限环，只需证明在式(14)成立条件下，下列雅克比行列式

成立即可，由定理1，经计算得到J≈-5.508 1×102≠0。

故通过扰动，系统(2)在正平衡点(1,1)处可分支出5个小振幅极限环。

参考文献：

[1]LLOYD N G,PEARSON J M,SAEZ E.Limit cycles of a cubic Kolmogorov system[J].Applied mathematics letters,1996,9(1):15-18.

[2]陆征一,何碧.三次Kolmogorov捕食系统的多个稳定极限环[J].工程数学学报,2001,18(4):115-117.

[3]LLOYD N G,PEARSON J M,SAEZ E,et al.A cubic Kolmogorov system with six limit cycles[J].Computers and mathematics with applications,2002,44(3/4):445-455.

[4]杜超雄,刘一戎,米黑龙.一类三次Kolmogorov系统的极限环分支[J].工程数学学报,2007,24(4):746-752.

[5]彭跃辉.一类具有两个正平衡点的Kolmogorov模型的极限环分枝[J].湘潭大学自然科学学报,2010,32(4):10-15.

[6]DU C X,WANG Q L,HUANG W T.Three-dimensional Hopf bifurcation for a class of cubic Kolmogorov model[J].International journal of bifurcation and chaos,2014,24(3):1450036.

[7]DU C X,LIU Y R,ZHANG Q.Limit cycles in a class of quartic Kolmogorov model with three positive equilibrium points[J].International journal of bifurcation and chaos,2015,25(6):1550080.

[8]聂文静,王辉,胡志兴,等.一类具有时滞和随机项的捕食-被捕食模型[J].河南科技大学学报(自然科学版),2015,36(6):75-81.

[9]HUANG W T,CHEN A Y,XU Q J.Bifurcation of limit cycles and isochronous centers for a quartic system[J].International journal of bifurcation and chaos,2013,23(10):255-259.

[10]陈莹,彭真,李静.两类五次平面多项式系统的中心判定[J].河南科技大学学报(自然科学版),2012,33(3):70-74.

[11]刘一戎,李继彬.论复自治微分系统的奇点量[J].中国科学(A辑),1989,32(3):245-255.

[12]刘一戎,陈海波.奇点量公式的机器推导与一类三次系统的前10个鞍点量[J].应用数学学报,2002,25(2):295-302.

[13]黄文韬.微分自治系统的几类极限环分支与等时中心问题[D].长沙:中南大学,2004.

[14]LIU Y R,LI J B.New study on the center problem and bifurcations of limit cycles for the Lyapunov system[J].International journal of bifurcation and chaos,2009,19(9):3791-3801.

中图分类号：O175.12

文献标志码：A

收稿日期：2015-12-25

作者简介：吴岱芩(1992-),女,四川达州人,硕士生;黄文韬(1966-),男,广西永福人,教授,博士,博士生导师,主要从事微分方程定性理论方面的研究.

基金项目：国家自然科学基金项目(11261013);广西高校重点实验室基金项目

文章编号：1672-6871(2016)03-0082-05

DOI:10.15926/j.cnki.issn1672-6871.2016.03.018