蒙特卡洛法评定坐标测量机直径测量不确定度

徐　磊，陈晓怀

(合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009)



蒙特卡洛法评定坐标测量机直径测量不确定度

徐磊，陈晓怀

(合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009)

摘要：工件完整的测量结果由测量估计值和测量不确定度组成，而坐标测量机在实际应用过程中，通常仅提供一个被测参数的估计值。以坐标测量机测量工件直径为例，阐述了测量过程中影响测量结果的不确定度来源，并讨论了坐标测量机面向任务的不确定度评定模型，给出基于测量不确定度表示指南和蒙特卡洛法的不确定度评定方法。最后，用某工件直径测量的不确定度评定实例验证所述方法的可行性。通过比较发现：当测量模型为非线性模型或输入量服从多种分布类型时，蒙特卡洛法更加准确、便捷。

关键词：坐标测量机；直径测量；蒙特卡洛法；不确定度评定

0引言

在进行工件测量时，完整的测量结果应包含测量估计值和测量不确定度。测量不确定度是表征被测量值分散性的非负参数。测量结果的可用性很大程度上取决于其测量不确定度的大小[1]。文献[2]依据测量不确定度表示指南(guide to the expression of uncertainty in measurement,GUM)对测量模型较为简单的测量系统进行测量不确定度的评定，简单有效，但对于坐标测量机(coordinate measuring machine,CMM)而言，该方法评定难度较大。这是由于CMM是一种复杂的几何量测量仪器，其测量策略的多样性使得不同测量任务的不确定度评定过程和结果大相径庭，且影响CMM测量不确定度的误差源因素很多，误差源与测量结果的传递关系难以确定[3-4]。文献[5]基于产品几何规范对CMM测量结果进行不确定度评定，该方法虽具可行性，但其复现性试验的合理规划是难点，测量人员需要有深厚的专业功底，且该方法需要大量试验数据，工作量较大。因此，CMM的测量结果通常只提供被测参数的估计值，不能给出测量任务的测量不确定度[6-7]。本文在CMM直角坐标系下，采用最小二乘法拟合圆，对工件直径测量的不确定度进行分析评定。分别采用GUM法和蒙特卡洛法(Monte Carlo method,MCM)对测量不确定度进行评定，并对两种方法进行了比较。研究内容对提高CMM测量不确定度评定的可靠性与可操作性，以及提升CMM的应用价值和空间，都具有一定的参考价值。

1测量模型

对应拟合圆时所采的测量点Pi(xi,yi)，则有正规方程组：

(1)

求解方程组(1)即可得到a、b、c，表示为：

(2)

CMM在圆的实际测量和评定过程中，一般会对采样点附加约束条件，即测量采样点数量为偶数，且在被测圆周上等间距分布。在此约束条件下最小二乘圆的圆心坐标[9]为：

(3)

(4)

求解式(4)，可得直径表达式为：

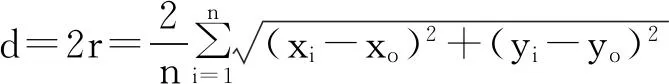
(5)

2测量不确定度评定模型

CMM测量直径时，影响测量结果的主要误差源包括仪器自身的21项机构误差、测量重复性误差、热变形误差、力变形误差、探测系统误差和动态测量误差等。因此，CMM测量直径D的一般数学表达式[10]为：

D=d+d(αW-αM)δθ+δres+δt+δv，

(6)

其中：d为测量模型的输出直径；αW为工件的热膨胀系数；αM为CMM光栅尺的热膨胀系数；δθ为实际测量温度与标准温度(20 ℃)的差值；δres为示值误差对测量结果的影响；δv为测量力对测量结果的影响;δt为动态误差对测量结果的影响。

直径D是关于输入量d、δθ、δres、δv、δt的函数，即：

D=f(d,δθ,δres,δv,δt)。

输入量之间互不相关，根据GUM法可得各传递因数[11]为：

于是，CMM测量直径D的合成标准不确定度为：

四是运行环境方面的问题。任何一项工作机制的运行，都需要一定的环境作为支撑。“一站式”司法确认机制得以建立，其根本原因是党和政府关于完善矛盾纠纷多元化解机制的基本要求。在这种条件下，完善工作机制、化解矛盾纠纷、维护社会稳定成为各级党委、政府和相关部门的一项重要任务，也就为“一站式”司法确认机制的建立创造了条件。该机制的运行，不仅需要司法机关、司法行政机关创造条件予以保障，同时也需要各级党委、政府、相关部门和组织，在思想理念、工作目标、工作机制等方面提供支持和保障，为该机制的运行创造良好环境。

(7)

同理，可分析得到u(d)。由式(5)知：

d=g(xi,yi,x0,y0)。

则各传递因数为：

(8)

于是，

(9)

将u(d)代入式(7)即得到被测直径D的标准不确定度uC(D)。

3蒙特卡洛法

蒙特卡洛法评定测量不确定度是基于分布传播的原理，适用于具有任意多个可由概率密度函数表征的输入量和单一输出量的测量模型，即需要已知模型中各输入量的概率分布，由评定模型计算出输出量的分布[12-14]。

图1　基于蒙特卡洛法的不确定度评定流程图

基于蒙特卡洛法的不确定度评定步骤如下：(Ⅰ)建立公式Y=f(xi)，即确定输出量与输入量之间的数学模型和测量不确定度的来源；(Ⅱ)分析确定各输入量的概率密度函数g(xi)和蒙特卡洛模拟次数M；(Ⅲ)通过计算机技术产生M组伪随机输入量，代入评定方程，得到输出量的M个值与分布函数的离散表示。将输出量的期望作为测量结果的估计值，输出量的标准偏差作为测量结果的标准不确定度，结合包含概率P，确定测量结果的包含区间，得出扩展不确定度。蒙特卡洛法评定测量不确定度的流程如图1所示。

4实例分析

采用海克斯康MH3D-DCC型三坐标测量机对车载空压机上壳体的直径进行测量，并评定其测量不确定度。试验所用坐标测量机空间长度测量精度MPEE≤(3+4L/1 000) μm，光栅尺的分辨率为0.1 μm。被测工件和机器光栅尺的热膨胀系数以及变化范围分别为：

αW=23.2×10-6℃-1；△αW=±4×10-6℃-1；

αM=10.5×10-6℃-1；△αM=±2×10-6℃-1。

将工件摆放在工作平面的中央，记录测量环境，采取自动测量的方法，锁定Z轴。在同一圆截面上等间距采样8个点来评价被测圆的直径。

表1　采样点的坐标值传递因数

重复测量10次获得各采样点的坐标值，计算单点坐标的不确定度u(xi)、u(yi)，为安全起见，选取其中的最大值作为最终的评价数据。通过试验数据计算知u(xi)≈u(yi)≤1.60 μm，则由式(3)计算可得u(x0)≈u(y0)≤0.57 μm。通过式(8)计算各传递因数，结果如表1所示。

根据式(9)计算得u(d)=1.10 μm。试验采用自动测量，测速较慢，测量力所引起的误差和动态误差可忽略不计。根据被测工件的标称尺寸计算知u(δres)=1.89 μm。试验室温度控制在(20±1) ℃，考虑均匀分布，则δθ=1 ℃，计算得：

根据式(7)计算标准不确定度为：

uC(D)=2.20 μm。

GUM法指出当输出量服从或近似服从正态分布时：

(Ⅰ)若自由度小，则根据韦尔奇-萨特思伟特(Welch-Satterthwaite)公式计算出自由度v，并由t分布表得到包含因子k。

(10)

该法需要计算出所有不确定度分量的自由度。

(Ⅱ)若自由度大，则当包含概率P=95%时，包含因子k默认取2.00;当P=99%时，k默认取3.00。在实际应用中，通常无法确定输出量的分布类型与自由度，但在不确定度报告中又需要给出扩展不确定度，此时包含因子k根据包含概率取2.00或3.00，即假设输出量服从正态分布。

若取P=95%，则k=2.00。GUM法获得测量结果的扩展不确定度为U=k·uC(D)=4.40 μm，包含区间为(67.064 0，67.073 8)。

4.2MCM评定结果

图2　蒙特卡洛法直径测量结果的分布图

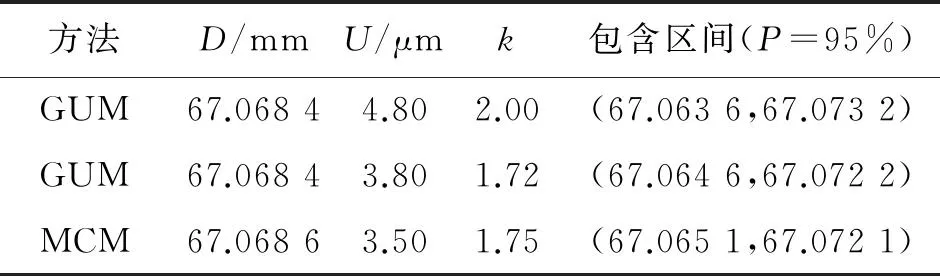
方法D/mmU/μmk包含区间(P=95%)GUM67.06844.802.00(67.0636,67.0732)GUM67.06843.801.72(67.0646,67.0722)MCM67.06863.501.75(67.0651,67.0721)

4.3评定结果对比

由图2可以看出：输出量近似服从梯形分布，与GUM法默认的服从正态分布不符。所以当包含概率P=95% 时，GUM法所采用的包含因子k不可取2.00，此时由梯形角参数与包含概率可得：k=1.72。则U=k·uC(D)=3.80 μm，包含区间为(67.064 6，67.072 2)。基于GUM法与MCM评定出的CMM直径测量的扩展不确定度，如表2所示。

对比评定结果可知：当包含因子k在不考虑输出量的分布，默认取2.00时的扩展不确定度比实际的扩展不确定度扩大了26%。

5结论

(1)MCM略过求解灵敏系数的过程，避免了GUM法在计算灵敏系数时忽略泰勒级数高阶项的误差和繁杂的计算。

(2)在测量不确定度评定模型复杂的情况下，运用MCM可有效简化测量不确定度的评定流程。

(3)MCM可由输出量的离散表示得出扩展不确定度，避免了GUM法中包含因子k的近似。

综上所述，当CMM测量模型为非线性等复杂的数学模型或输入量服从多种分布类型时，基于蒙特卡洛法评定测量不确定度更加准确、便捷。

参考文献：

[1]国家质量监督检验检疫总局.测量不确定度评定与表示:JJF 1059.1—2012[S].北京:中国质检出版社,2012.

[2]张孝军,程银宝,吴军,等.数字式功率计检测电磁灶热效率测量结果不确定度评定[J].计量与测试技术,2013,40(7):48-49.

[3]张国雄.三坐标测量机[M].天津:天津大学出版社,1999.

[4]陈晓怀,李红莉,杨桥,等.坐标测量机面向任务的测量不确定度评定[J].计量学报,2015,36(6):579-583.

[5]杨桥,徐磊,姜瑞.基于GPS的三坐标测量机不确定度评定[J].计量与测试技术,2014,41(9):1-2.

[6]叶德培.测量不确定度理解评定与应用[M].北京:中国质检出版社,2013:1-9.

[7]陈晓怀,王汉斌,程银宝,等.基于测量不确定度的产品检验中误判率计算[J].中国机械工程,2015,26(14):1847-1850,1856.

[8]马向南,李航,刘丽丽,等.最小二乘改进算法及其在椭圆拟合中的应用[J].河南科技大学学报(自然科学版),2014,35(3):18-21.

[9]李飞,雷贤卿,崔静伟,等.圆度误差的二分法逼近搜索评定[J].河南科技大学学报(自然科学版),2014,35(2):20-23.

[10]李高峰.三坐标测量机形状误差测量不确定度评定[D].合肥:合肥工业大学,2013.

[11]费业泰.误差理论与数据处理[M].6版.北京:机械工业出版社,2010.

[12]陈怀艳,曹芸,韩洁.基于蒙特卡罗法的测量不确定度评定[J].电子测量与仪器学报,2011,25(4):301-308.

[13]石照耀,张宇,张白.三坐标机测量齿轮齿廓的不确定度评价[J].光学精密工程,2012,20(4):766-771.

[14]国家质量监督检验检疫总局.用蒙特卡洛法评定测量不确定度:JJF 1059.2—2012[S].北京:中国质检出版社,2012.

中图分类号：TB92

文献标志码：A

收稿日期：2015-11-11

作者简介：徐磊(1993-),男,安徽滁州人,硕士生;陈晓怀(1954-),女,安徽怀宁人,教授,博士,博士生导师,主要研究方向为现代精度理论与应用.

基金项目：国家自然科学基金项目(51275148)

文章编号：1672-6871(2016)03-0015-04

DOI:10.15926/j.cnki.issn1672-6871.2016.03.004