双臂电桥测低值电阻的等/非等精度测量不确定度评定

张莎+张怡+海莲+张欢

摘 要 以双臂电桥测低值电阻电阻率的实验数据处理为例，本文研究等精度测量的不确定度评定方法及非等精度测量的两种不确定度评定方法，探讨不等精度测量中B类不确定度对处理结果的影响。并且给出了针对具有两个线性变量而其它待测量真值不变的多待测量实验的不确定度的直线拟合法，且由实验数据的对比分析表明了其合理性和准确性。

【关键词】双臂电桥 等精度测量 非等精度测量 不确定度评定

1 引言

直流双臂电桥测低值电阻电阻率是一个广泛开展的综合性大学物理实验，其不同于中学的测量电阻的方法和对间接测量量的不确定度评定对引导学生理解大学物理和中学物理的异同上发挥着重要作用；对开拓学生的物理思维和启发学生运用不同方法测量物理量方面具有重要的意义。在双臂电桥测电阻时可以采用电阻长度不变的等精度测量和电阻长度变化的非等精度测量（广义的非等精度测量）两种方案。对不同方案，处理不确定度时应该选择不同的处理方法。等精度测量数据的不确定度有各类教材和参考书可做参考；部分论文对其它实验的非等精度的不确定度进行了处理，但不同的不确定度处理方法的结果之间或者非等精度和等精度测量的处理结果间的比较存在较大差异，而本实验非等精度测量的不确定度评定却未见提及。但我们在开展该实验时统计发现，在同学们自由选择的情况下，有超过2/3的学生会选择非等精度测量；而即便是在刻意引导下，也有接近1/4的学生采用非等精度测量。在处理不确定度时，绝大多数的学生却使用了间接测量量的等精度不确定度评定方法，这导致大部分采用非等精度测量方案的同学处理的不确定结果不合理。可见本实验中，非等精度的不确定度评定是不可避免的内容。为此，本文给出了非等精度测量时电阻率的不确定度评定方法；探讨了加权平均法和直线拟合法的A类不确定度和B类不确定的处理。并对等精度和非等精度测量结果的不确定度进行了对比分析。本文对非等精度的不确定度评定方法，可以为多个待测量中存在两个线性变量而其它待测量真值不变情况下的不确定度处理提供参考。

2 等精度测量及不确定度评定

本实验的电阻率采用间接测量，选用足够长的直径均匀的圆柱形低值电阻，分别测量电阻阻值、电阻直径D和长度L，通过电阻率公式

计算电阻率。等精度测量时，固定长度L真值不变，在相同条件下重复测量各物理量6次。为了与后面不等精度数据的不确定度对比，我们分别测量了L分别约为419.8mm、399.9mm、380.0mm、360.0mm、340.0mm和320.0mm的数据，每个L等精度测量六组（篇幅所限，测量原始数据未列出）。

等精度测量结果的不确定度，根据误差传递公式：

，先分别计算L、D和Rx的不确定度u（x），（其中，x=L、D、Rx），再由误差传递公式求出电阻率的不确定度u（ρ）。其步骤如下：

（1）计算x（x=L、D、Rx）的A类不确定度。A类不确定度是用统计学方法计算的分量，是随机误差性质的不确定度。可视为实验的标准偏差：

。

（2）计算x（x=L、D、Rx）的B类不确定度。B类不确定度，不满足统计规律的分量，是系统误差性质的不确定度。通常考虑仪器误差引起的不确定度：

，其中△mL=0.1mm，

△mD=0.004mm，。

（3）计算x（x=L、D、Rx）的合成不确定度：

。

（4）计算x（x=L、D、Rx）的相对不确定度：

。

（5）计算电阻率ρ的不确定度：

；

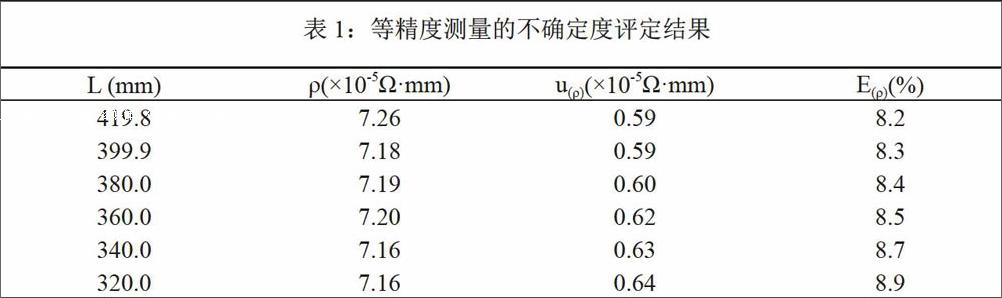
为了与后面不等精度数据的不确定度对比，对于每个L处等精度测量的六组数据，我们都计算了其不确定度，结果列于表1。根据我国制定的不确定度实施指南，且为体现其差异性，表示不确定度时取两位有效数字。由表中可以看出，隨着L的增大，不论是实验的标准偏差还是相对不确定度都逐渐减小。因此，对于等精度测量，为了减小误差，应选择较大的L进行测量。

3 非等精度测量数据的加权平均法处理

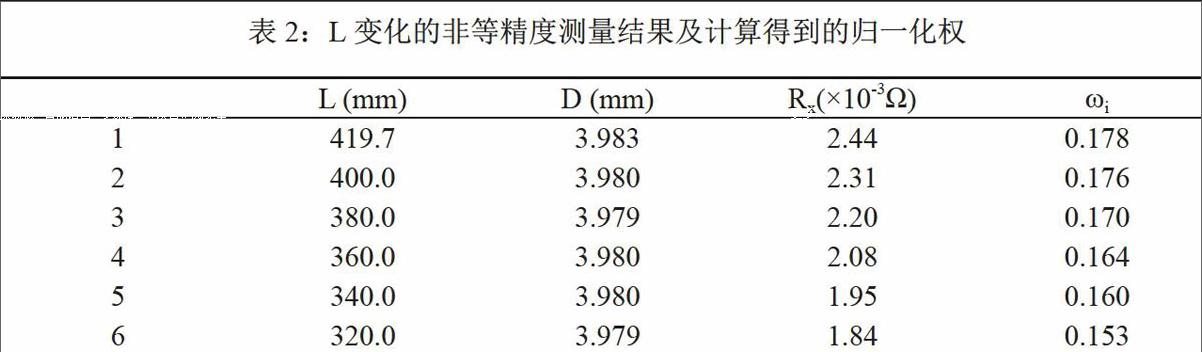
相比于L固定的等精度测量，实验中还可采用改变L的非等精度测量电阻率的方案，采用这种方案，实验过程具有变化性，操作不显枯燥，更容易引起学生的兴趣。表2给出了L等间距变化测量的六组数据。对其数据的处理有加权平均法和直线拟合法两种方式，两种数据处理不确定度的方法有一定的差异。此部分给出了加权平均处理A类和B类不确定度的方法。

3.1 最佳值ρO

从第二部分等精度测量结果的不确定度变化趋势可知，L越小，测量结果的误差越大，因此，ρ的最佳值不能直接平均求得，而应考虑单次测量的可靠程度。即最佳值ρ0表示为加权平均值：ρ0=∑iωiρi，其中ρi为第i次单次测量计算结果，ωi为其对应的归一化权。ωi与单次测量的不确定度u（ρi）的关系为：

。计算u（ρi）时，因为其为单次测量的不确定度，因此不计入A类评定而只考虑B类评定为：

，其中，△mL=0.1mm，△mD=0.004mm，

。

计算得ρ0=7.19×10-5Ω·mm，略大于其平均值=7.18×10-5Ω·mm。由表2列出的权值ωi的计算结果可见，随着 L增大，权值逐渐增加，这符合本实验仪器的误差变化规律。

3.2 A类不确定度

类似等精度测量的A类不确定度，但需计入加权平均。通常将加权平均的标准偏差记为其A类不确定度：

。计算结果为：uA（ρ）=0.016×10-5Ω·mm。

3.3 B类不确定度

大部分参考书和文献[1-4]的非等精度测量不确定度评定只考虑了A类不确定度，但本实验中，上述计算结果显示，若只考虑A类评定，其结果与等精度测量的处理结果有很大差异。由于B类不确定度是系统误差性质的不确定度，且考虑其权重，参考李震春等老师在伏安法测表头内阻实验中所采用的处理方法，我们将单次测量的不确定度u（ρi）的加权平均作为B类不确定度：uB（ρ）=∑iωiu（ρi）。计算结果为：uB（ρ）=0.610×10-5Ω·mm

3.4 合成不确定度

将A类和B类不确定度按其方和根法计算得：

u（ρ）=

=0.61×10-5Ω·mm；

其最终结果为：ρ=（7.19±0.61）×10-5Ω·mm（P=68.3%），E（ρ）=8.5%。

4 非等精度测量数据的直线拟合法处理

本实验中，测量电阻阻值Rx、电阻直径D和长度L三者之间虽然不具备线性关系，但根据电阻率公式以及表2非等精度的测量结果看，电阻阻值Rx与电阻长度L存在线性关系。我们引入一个中间量k，定义为：

，则电阻率表示为。根据k和直径D的特点，我们提出，ρ的最佳值根据公式

确定，而其不确定度根据误差传递公式来计算。

4.1 直径D的不确定度评定

直径D的不确定度评定采用与第二部分中等精度测量的相同处理方法，计算得到：

=3.9802mm；u（D）==0.0024mm；E（D）=0.060%。

4.2 中间量k的最佳值和不确定度评定

根据Rx=kL，（Rxi，Li）的测量值可用过原点的直线来拟合，其斜率k的最佳值可表示为：k=（∑iLiRxi）/∑iL2i。计算结果为：k=5.78×10-3Ω/mm。

k的A类不确定度一般为拟合直线中斜率k的标准偏差：

。计算得到uA（k）=0.011×10-3Ω/mm。显然，k的A类不确定度较小，若只考虑A类不确定度，其最终结果仍与前面计算结果有很大差异。因此，我们进一步计算了k的B类不确定度。

由于B类不确定度是系统误差性质的不确定度，考虑本部分为直线Rx=kL拟合结果，我们将直线中处的单次测量不确定度作为k的B类不确定度，其实质为直线上该处的仪器误差，即：

，

其中。计算得：uB（k）=0.489×10-3Ω/mm。

综上，可以得到中间量k的最佳值和不确定度分别为：k=5.78×10-3Ω/mm；u（k）==0.49×10-3Ω/mm；E（k）=8.5%

4.3 ρ的直线拟合法数据不确定度处理结果

将D和k的不确定度按误差传递公式计算得：

u（ρ） =

=0.61×10-5Ω·mm；

E（ρ）==8.5%。

5 三种方法不确定度比较分析

根据以上结果可知：

（1）比较等精度测量的不确定度结果发现，L真值较大时，实验误差更小。

（2）非等精度测量的不确定度评定时：若不计入B类不确定度，结果与等精度处理结果有很大差异；采用本文的方法计入B类不确定度，其结果与介于L=380cm到L=360cm的等精度处理结果非常接近。由此可见，非等精度不确定度评定时，若不计算B类不确定度是不合理的，在处理非等精度不确定度时，仍应该考虑B类不确定度。

（3）两种非等精度數据处理方法得到的结果一致。本实验中所采用的加权平均法与大部分实验所使用的加权平均法相同，且与等精度测量的不确定度相近，其结果的准确性能够得到认可。而本实验中所改进的直线拟合法处理的结果与加权平均法一致，可见我们提出的对具有两个线性变量而其它待测量真值不变的多待测量实验的不确定度评定方法是合理可行的。

6 结论

本文讨论了直流双臂电桥测低值电阻电阻率实验中，等/非等精度测量不确定度评定的方法与步骤，结果的分析对比发现，等精度测量时，为减小误差，应尽可能的选择较大的L进行测量；非等精度测量时，B类不确定度对结果具有很大影响不可忽略。本文对非等精度测量中不确定度的直线拟合处理法进行了改进，提出了针对具有两个线性变量而其它待测量真值不变的多待测量实验的不确定度的直线拟合法。从数据的处理结果来看，该方法合理可行，对具有类似特征的多待测量实验具有较大的参考价值。

参考文献

[1]訾振发，赵敏，章韦芳.不确定度理论在重力加速度测量实验中的应用[J].合肥师范学院学报，2013，31（06）：63-65.

[2]原媛，沈元华，赵在忠，金浩明，马秀芳，孙燕青，马世红.惠斯通电桥实验中对互易桥臂测量结果的不确定度评定[J].物理实验，2014，34（07）：33-36.

[3]徐红，曹冬梅.非等精度测量电阻的数据处理[J].价值工程，2012，03：0262-0263.

[4]张德根.单摆实验中不等精度测量的不确定度分析[J].大学物理实验，2013，26（06）：0092-0094.

[5]李震春，左卫群，曾卫东.非等精度测量方案数据处理方法的探讨[J].广西物理，2007，28（04）：44-47.