尺寸链技术在工艺优化中的应用

孔令伟，张浩

（华晨汽车工程研究院，辽宁 沈阳 110141）



尺寸链技术在工艺优化中的应用

孔令伟，张浩

（华晨汽车工程研究院，辽宁 沈阳 110141）

摘 要：尺寸链技术是机械制造业中重要的基本理论之一，在设计、工艺以及检验等领域都有着广泛的应用。随着科技的进步以及市场竞争的愈演愈烈，如何降低生产成本，提高产品质量是每个企业都不能忽视的话题，因此各大主机厂都更加重视尺寸链技术。文章着重对尺寸链技术在工艺优化方面的应用进行了研究。

关键词：尺寸链；车身精度 ；工艺优化

10.16638/j.cnki.1671-7988.2016.03.052

CLC NO.: U468.3 Document Code: A Article ID: 1671-7988(2016)03-161-04

前言

产品制造的基本要求就是成本低，质量好。能否实现在提高产品质量的同时还能有效的降低生产成本，这是由产品设计、生产工艺等因素共同决定的。但是在产品设计中沿袭已有产品或者凭借已有经验是一种普遍存在的现象，而重视结构而忽略工艺性也是十分严重的倾向。在实际生产中，如果应用尺寸链技术合理安排工艺顺序，可以在不增加生产成本的同时有效提高产品质量。尺寸链计算是一种相对比较成熟的技术，国内外都发表过尺寸链技术的相关文章。例如Bryan Fischer 的尺寸链专著[1]对尺寸链技术做了详尽的表述；林忠钦教授发表的装配偏差研究方法[2]一文，在文中详细列举了轿车车体装配偏差研究方法的种类，以及未来的发展方向。J.Jin 和 J.Shi[3]在 1999 年发表了针对钣金件偏差分析模型的研究。本文以某车型前桥安装点工艺优化方案为例，详细说明了尺寸链计算在工艺优化中所起到的作用。

1、尺寸链中的误差传递系数

在尺寸链计算中，封闭环的误差是由各组成环误差共同作用的结果，而各组成环也不可避免的存在误差，各组成环误差按照一定的比例系数ζi独立作用于封闭环，并对封闭环误差产生影响。这个比例系数ζi被称为误差传递系数。

误差传递系数ζi不仅有数值的大小，还有方向，它表示了该组成环误差对封闭环误差的影响结果以及方向。一般来讲，在线性尺寸链中传递系数一般为1，其中增环误差传递系数为+1，减环误差传递系数为-1。

2、极值法计算尺寸链

2.1 用极值法计算的先决条件

(1) 使用极值法计算的不是单一产品或零件的封闭环误差，而是一批产品或零件的误差；

(2) 在要求完全互换的条件下，需要使用极值法计算尺寸链。所谓完全互换是指在大批量生产条件下，只要各组成环的误差均控制在所设定的公差带内，就可以百分之百保证产品合格。因此封闭环极限误差是按照最坏情况考虑的。这种最坏情况是：组成环的误差控制在设计公差范围内，但不是最大极限尺寸就是最小极限尺寸；对于装配来说，往往是增环的最大极限尺寸与减环最小极限尺寸相遇或者是增环最小极限尺寸与减环最大极限尺寸相遇。

2.2 封闭环的公称尺寸

尺寸链中组成环的公称尺寸本身是一个计算误差的基准值，不存在误差。在线性尺寸链中，封闭环公称尺寸满足下列公式：

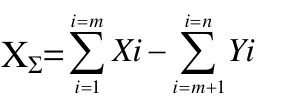
式中：XΣ-封闭环的公称尺寸

2.3 封闭环的极限误差

按照原始误差独立作用原理，封闭环极限误差上限是所有增环误差达到上偏差与所有减环误差达到下偏差时独立作用于封闭环的误差总和。

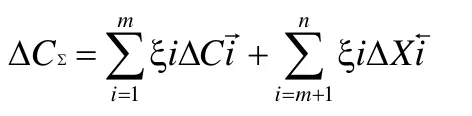
同理，封闭环误差下限的计算公式如下：

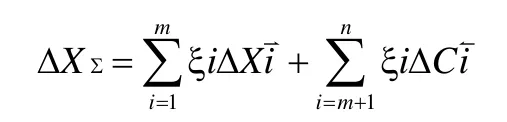
式中：ΔCΣ-封闭环误差上限；

ΔXΣ-封闭环误差下限；

ξi -各组成环误差传递系数；

ΔCi-组成环误差上限；

ΔXi-组成环误差下限；

向右剪头表示增环，向左剪头表示减环。

3、概率法计算尺寸链

3.1 概率法计算尺寸链的使用条件

在组成环及封闭环都服从正态分布的情况下，可以使用概率法计算尺寸链。正态分布是一个连续函数，而对于产品误差来说，只有数量足够大才能构成连续的随机变量分布，而小批量只能构成离散型随机变量分布。因此使用概率法计算尺寸链的首要条件便是产品数量足够大。

3.2 封闭环的均方根偏差δΣ

设尺寸链中各组成环的误差是互不关联的独立偶然量，他们的均方根偏差分别为：

其分别对应的误差传递系数为：

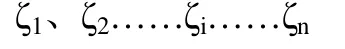
因此，有如下公式：

如前所述，在线性尺寸链中传递系数一般为1，其中增环误差传递系数为+1，减环误差传递系数为-1。

4、蒙特卡洛法计算尺寸链

4.1 蒙特卡洛法简介

蒙特卡洛（Monte-Carlo）法，又称统计试验法或随机模拟法。是一种通过随机变量的统计试验、随机模拟求解数学、物理以及工程技术问题近似解的数学方法。

蒙特卡洛法的理论基础是概率论中的大数定律，因此需要获得大量的统计数据才能保证计算结果的准确可靠，这极大限制了蒙特卡洛法在实际生产中的应用。但是随着计算机技术的不断普及和提高，这种限制已被大大减弱。

4.2 蒙特卡洛法计算尺寸链基本原理

（1）利用计算机产生多个伪随机数，分布区间在0-1之间：

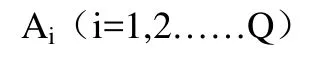
（2）如果组成环趋近于正态分布，则可通过将均匀分布的随机数Ai变换成标准正态分布N（0,1）的随机数，其变换公式如下：

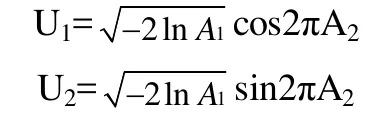
式中U1、U2为相互独立且服从N（0,1）分布的随机数。

（3）由于各组成环尺寸的均方根差σ2不一定等于1，所以还要将U1、U2……UQ变换成服从N（0, σ2）分布的随机数H1、H2……HQ，并且按±3σ的范围截尾；Hi就是符合各组成环尺寸分布特性的随机变量：

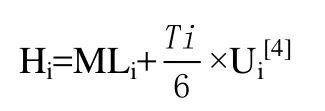
式中：MLi-第i个组成环的中间尺寸数值。当服从正态分布时，即为第i个组成环的算术平均值（数学期望）；

Ti-第i个组成环的尺寸公差；

（4）利用模拟的一组Hi值，通过尺寸链方程求得一系列的封闭环尺寸Ni值；

（5）求出封闭环的基本尺寸和公差。

上述重复计算Ui、Hi、Ni的次数Q就是抽样次数，也就是样本大小；抽样次数（样本）越大，置信度越高，分布函数拟合得就越好。

5、尺寸链计算结果分析

5.1 问题分析

以使用概率法计算某车型前桥安装点位置公差为例，介绍尺寸链计算在工艺优化中的应用。

某车型前桥安装点按照原有焊接工艺方案，尺寸链计算结果如表1所示：

图1　尺寸链组成环示意图

表1　尺寸链计算表

通过尺寸链计算可知前桥安装点尺寸精度无法控制在±1以内。

经过分析，前桥安装点最终尺寸的形成过程如下图2所示：

图2　轮罩总成焊接顺序

前桥安装点从单件到形成最终尺寸一共经历了三个焊接工位，每个工位的误差累积最终导致前桥安装点尺寸超差。

5.2 尺寸链计算结果风险接收标准

对于车身刚性连接件（如座椅安装、发动机、变速器安装等），由于无法通过返修手段消除缺陷，因此尺寸链计算结果必须在设定公差带范围内。

在此项目中，底盘部门对车身前桥安装点设定的尺寸公差为±1，由于前桥安装属于车身刚性连接，无法通过返修消除缺陷，因此车身前桥安装点尺寸公差需要控制在±1范围内。

5.3 工艺优化方案

通过对焊接工艺进行分析可知，轮罩总成焊接顺序如图3所示：

图3　安装点所在腔体示意图

通过观察轮罩总成焊接顺序发现，前桥安装点所在封闭腔体在轮罩总成工位形成（如图3所示）。

因此可以将前桥安装点移到前纵梁分总成工位焊接，减少前桥安装点尺寸形成工序数量，减少公差累计。

焊接工艺优化方案如下：

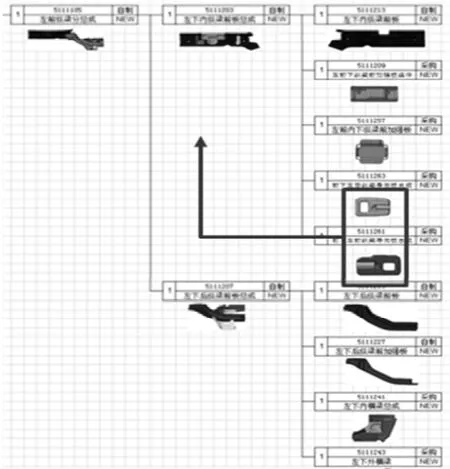
图4　焊接顺序优化方案

图5　优化后尺寸链组成环示意图

表2　尺寸链计算表

经过尺寸链计算，使用经过优化的焊接工艺方案，前桥安装点尺寸精度为±0.82，可以有效控制在±1范围内，满足底盘安装要求。

经过优化后的焊接工艺，前桥安装点最终尺寸的形成过程如下图6所示：

图6

通过尺寸形成图可知，在优化后的焊接工艺中，前桥安装点最终尺寸的形成减少了一个焊接工序，封闭环误差也随之有效降低。

6、结论

本文以提高某车型前桥安装点位置精度为例，研究了尺寸链技术在工艺优化中的应用，得到以下结论：

（1）尺寸链技术可以有效预测安装点位置精度。

（2）通过尺寸链计算可以有针对性的指导工艺优化。

（3）尺寸链计算结果表明，尽可能通过结构设计减少尺寸链组成环数量，减小或消除计算结果超差风险。

（4）焊接顺序的改变必然会导致焊接方式、搭接形式、零件结构的变化，因此在优化焊接工艺时要全面考虑，以免产生问题隐患。

参考文献

[1] Brain Ficher, Mechanical Tolerance Stackup And Analysis[M].CRC Press.2011.

[2] 林忠钦等.轿车车体装配偏差研究方法综述[J].机械设计与研究,1999,No.3:58-60.

[3] J.Jin, J.Shi.State space modeling of sheet metal assembly for dimensional control[J].ASME Journal of Manufacturing Science and Engineering, 1999, 121: 756-762.

[4] 中山大学数学力学系.概率论与数理统计(上、下册).北京.高等教育出版社,1980,下册，343-344,363.

Study on the application of dimension chain technology in process optimization

Kong Lingwei, Zhang Hao
（Brilliance Automotive Engineering Research Institute, Liaoning Shenyang 110141）

Abstract:Dimension chain is one of the basic theories in the mechanical manufacture field, it has a wide range of applications in many fields, such as design, process and so on.With the progress of science and technology and the intensified competition in the market, how to reduce the production cost and improve the quality of the products are becoming a subject that every company can't ignore, so mainframe factories are all paying more attention to dimension chain technology.This paper focuses on the application of dimension chain technology in process optimization.

Keywords:Dimension chain; precision of body; process optimization

作者简介：孔令伟，就职于华晨汽车工程研究院尺寸工程室。

中图分类号：U468.3

文献标识码：A

文章编号：1671-7988(2016)03-161-04