纸张经典渗吸模型相互关系仿真分析与理论推导

刘国栋， 成囡囡， 王　月, 马　欣， 王　哲

(1.陕西科技大学 轻工与能源学院 陕西省造纸技术及特种纸品开发重点实验室, 陕西 西安　710021; 2.陕西青年职业学院, 陕西 西安　710068)



纸张经典渗吸模型相互关系仿真分析与理论推导

刘国栋1， 成囡囡1， 王月2, 马欣1， 王哲1

(1.陕西科技大学 轻工与能源学院 陕西省造纸技术及特种纸品开发重点实验室, 陕西 西安710021; 2.陕西青年职业学院, 陕西 西安710068)

摘要：针对纸张渗吸过程中不同毛细力学系统支配下所建立的经典渗吸模型：纯惯性力渗吸模型、Bosanquet渗吸模型和Lucas-Washburn渗吸模型.在统一的物理参数下，通过模型渗吸仿真分析和数学理论推导的方式，揭示了经典渗吸模型之间存在的相互关系.同时，在渗吸分析的基础上，讨论了经典渗吸模型应用的特定情况，为纸张渗吸行为的精确描述提供切实的理论依据.

关键词：纯惯性力渗吸模型； Bosanquet渗吸模型； Lucas-Washburn渗吸模型

0引言

印刷油墨等流体在纸张上的呈色表现是通过流体与纸张的相互作用来完成，该过程通常称为流体(油墨)在纸张中的渗透[1]或者渗吸[2].在不考虑外在压力的情况下，油墨流体在纸张中的传输过程主要表现为毛细力学系统的自发渗吸.所谓自发渗吸(简称渗吸)是多孔介质在毛细管力驱动下自发地吸入某种润湿液体的过程[3].当油墨流体与纸张发生作用时，在毛细力学系统的支配下，油墨的流相层(连接料等)渗吸到纸张中，油墨的颜料颗粒在纸张表面附着固化后形成图文.因此，纸张渗吸特性的优劣直接决定着渗吸过程中油墨的传输及渗吸后形成的印刷质量.纸张渗吸行为描述时，通常将纸张介质等效为毛细管结构来研究纸张的渗吸特性，常见的经典渗吸模型有Lucas-Washburn模型(简称L-W模型)[4]，Bosanquet模型[5,6]和纯惯性力模型[7]三种模型，这三种模型分别在不同的力学系统中描述流体在纸张等多孔介质中的渗吸.在上述模型的应用中，几乎所有中文文献都在利用L-W模型描述油墨等流体在纸张中的渗吸行为.但是Schoelkopf[8]和Ridgway等[9]在研究涂布纸涂层材料渗吸时，观察到了L-W模型描述渗吸与实验渗吸的偏差，并分析了造成这种偏差的原因可能在于流体渗吸过程中的惯性力，提出了应该利用考虑惯性力因素的Bosanquet模型来描述涂布纸涂层材料的渗吸.与此同时，Quere[10]通过实验观察证实了流体在毛细管中的惯性流动，并提出了纯惯性力支配的渗吸模型.刘国栋[11]在研究涂层材料渗吸时，证实了惯性力在渗吸初期存在的积极作用，一定程度上证明了纯惯性力模型在描述渗吸过程初期阶段的可行性.

因此本文针对经典渗吸模型优势及不足，在统一渗吸物理参数下，对比分析及验证上述经典渗吸模型在描述纸张渗吸行为的具体表现及可行性，为纸张渗吸特性的准确描述提供可靠的理论依据.

1表征纸张渗吸行为的经典模型

1.1纯惯性力支配的渗吸模型

当流体与纸张接触的初期，由于渗吸流体质量很小，对应的自身重力和粘性阻力也很小，在渗吸力学系统中，可将自身重力和粘性阻力忽略不计，因此起主要支配作用的是毛细力和惯性力.针对此种物理情形，渗吸模型[10]的表达如(1)式所示.

(1)

通过求解非线性微分方程，可得纸张渗吸等效毛细管渗吸的表达式，如式(2)所示：

(2)

其中h为渗吸的深度，θ为接触角，γ为流体表面张力，R为毛细管等效半径，ρ为流体的密度.从上式(2)可以看出，渗吸深度随渗吸时间是线性变化的关系.

1.2Bosanquet渗吸模型

在渗吸过程中，随着渗吸流体的进一步上升，吸收量不断增加，与之对应的自身重力和粘性力也变得越来越明显，与毛细驱动力和惯性力一起共同作用渗吸过程.考虑到在该阶段初期的自身重力仍较小，可以忽略不计.因此Bosanquet[5]提出了忽略流体重力因素的渗吸模型(η为流体粘度)，如式(3)所示.

(3)

求解(3)可得

(4)

其中

从上述公式(4)中可以看出，Bosanquet渗吸模型所描述渗吸量与渗吸时间并非成简单的线性关系，其计算过程略显复杂.

1.3Lucas-Washburn渗吸模型

随着渗吸的进行，流体粘性阻力不断增大，与毛细驱动压力的相互抵消作用也越来越明显，净驱动力越来越小，同时流体流动的惯性力也越来越小.因此在忽略流体自身重力和惯性效应下，受粘性力和毛细力共同支配Lucas-Washburn渗吸模型，如公式(5)所示(其中η为流体粘度).

(5)

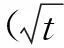
对比分析上述三种经典渗吸模型的建立过程及表达式，可以看出上述模型分别建立在不同的力学支配系统下，相关文献[12-14],也分别在各自的物理情形和参数下，描述了上述渗吸模型在纸张渗吸表征中的应用.但是究竟纸张的渗吸过程确切适合哪种模型及受何种力学系统支配却一直未见相关报道，仍需进一步分析对比.

2经典渗吸模型相互关系的数学意义证明

对于Bosanquet渗吸方程而言，其表现形式正如公式(4)所示：

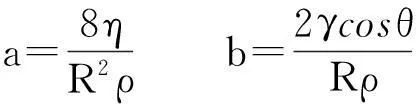
在初始的渗吸过程中，当at<<1时，利用泰勒级数展开公式可得[15]

(6)

将式(6)代入到(4)可得

(7)

其中h1是起始位置的渗吸深度，h2是任意时刻t的渗吸深度.

(8)

当渗吸的起始位置x1=0时，公式(8)将变为

(9)

公式(9)与纯惯性力阶段描述的渗吸模型是一致的，因此在初期的渗吸过程中(即当at<<1时)，纯惯性力渗吸和Bosanquet渗吸是等效的.

另外，将公式(4)进行如下的变形,

(10)

由于

(11)

因此

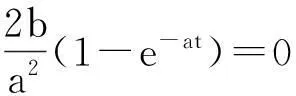
即渗吸过程中，当物理参数：

(12)

对于一些高密度和低粘度的流体，公式(12)所描述的物理情形很容易达到.而这种流体常常用于油墨中的连接料，如正十六烷、矿物油、乙二醇、亚麻籽油和异三十烷等，都属于高密度和低粘度的油墨流体.因此从式(10)～(12)可以看出，Bosanquet渗吸方程就演变为Lucas-Washburn方程，即在渗吸过程中Bosanquet渗吸行为会逐渐转换成Lucas-Washburn渗吸.

3经典渗吸模型的对比分析

结合上述推导的经典模型的相互关系，进一步确定纸张渗吸过程中，基于何种渗吸模型及毛细力学支配系统，需要在统一的物理参数下对上述模型进行对比仿真分析.由于正十六烷和矿物油作为常见的水基油墨和脂性油墨的载体已经得到了普遍的应用，本文以正十六烷(Sigma-Aldrich Chemie GmbH，D-89555，斯坦海姆，德国)和矿物油(PKWF 4/7 af new，Haltermann，德国)作为渗吸流体，具体的物理参数见表1所示.纸张介质的毛细管等效半径R分别设定为1μm，500μm，1 mm三种.纸张等多孔材料等效毛细管对正十六烷和矿物油的润湿接触角为0[16].

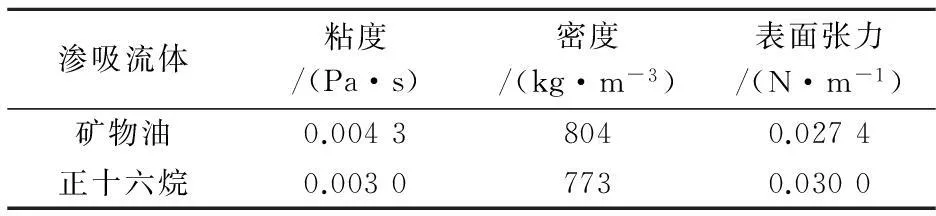
表1　渗吸流体的物理性能参数[8]

基于Matlab计算软件平台，对上述模型进行编程实现，为了更清楚的对比分析渗吸模型存在的相互关系，渗吸过程分别用较短的渗吸时间轴和较长的渗吸时间轴来表示，较短的时间轴可以清楚看出渗吸初期的变化，较长的时间轴可以看出渗吸后期的变化，如图1～12所示.其中，图1、图3、图5、图7、图9、图11为渗吸模型渗吸初期的对比变化结果，图2、图4、图6、图8、图10、图12为渗吸模型后期的对比结果.

(1)毛细管等效半径R=1μm时的渗吸模型仿真结果见图1～4.

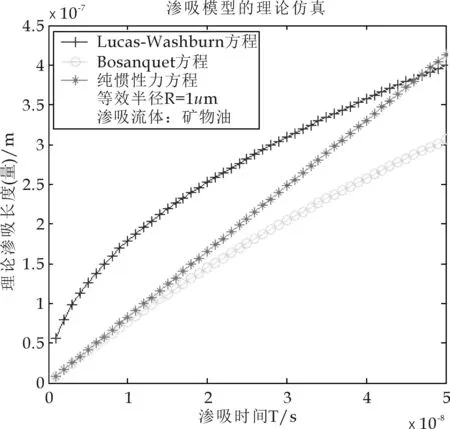
图1　渗吸初期对比图(矿物油，R=1 μm)

图2　渗吸后期对比图(矿物油，R=1 μm)

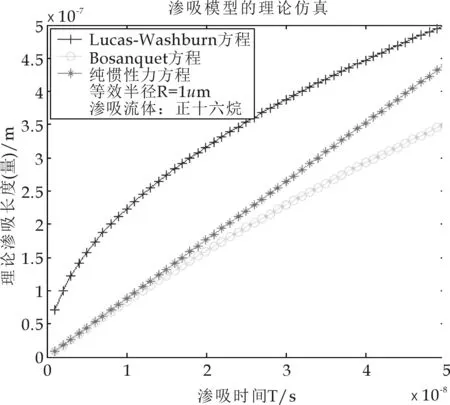
图3　渗吸初期对比图(正十六烷R=1 μm)

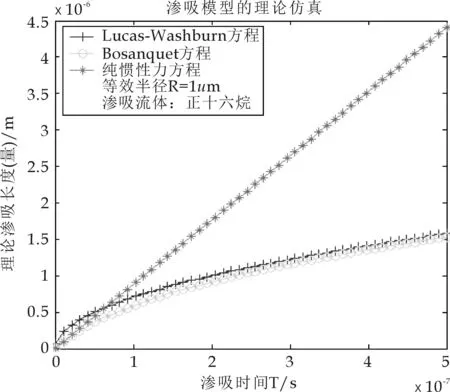
图4　渗吸后期对比图(正十六烷，R=1 μm)

(2)毛细管等效半径R=500μm时的渗吸模型仿真结果见图5～8.

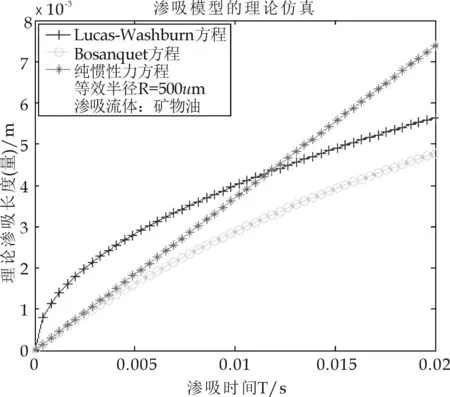
图5　渗吸初期对比图(矿物油，R=500 μm)

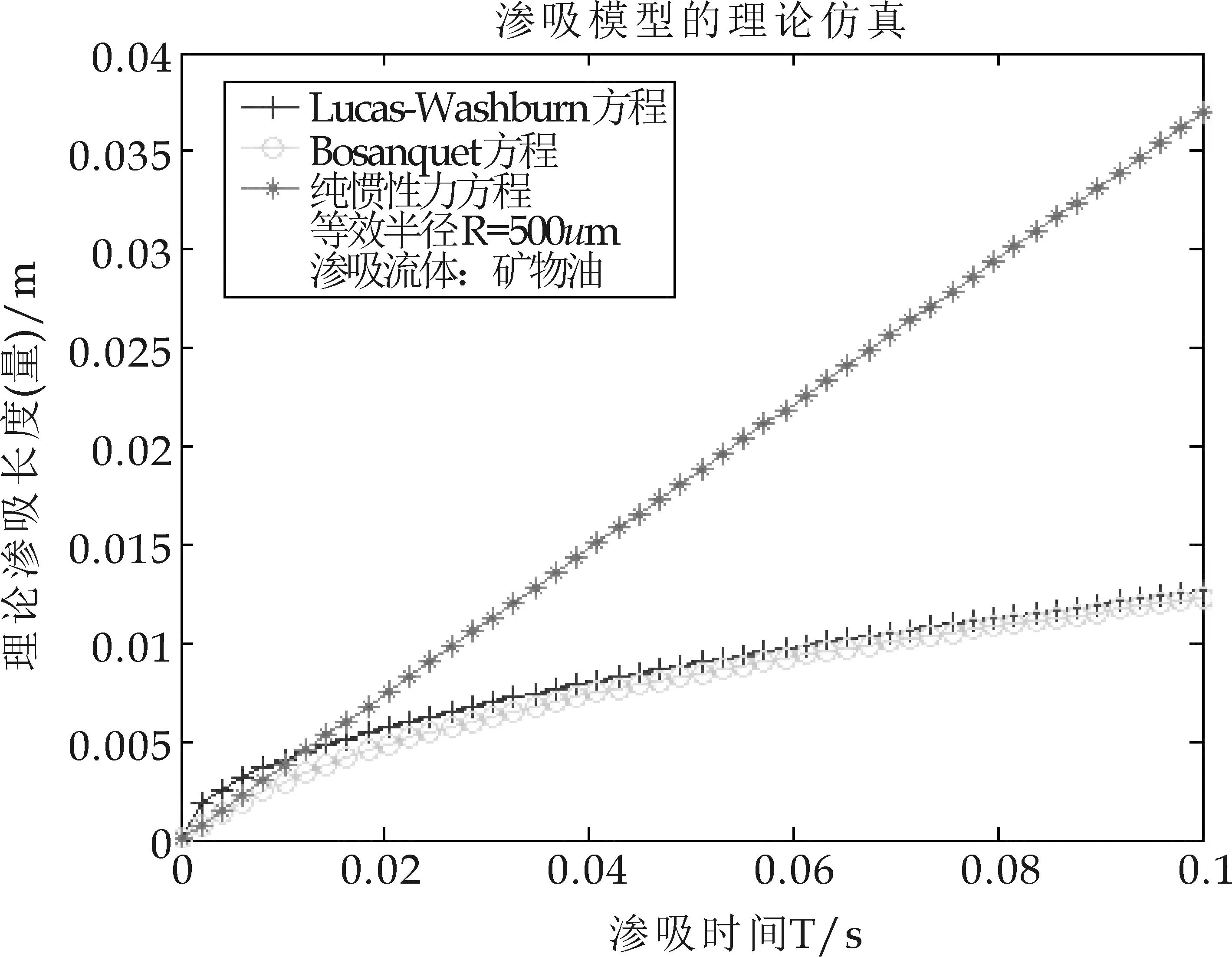
图6　渗吸后期对比图(矿物油，R=500 μm)

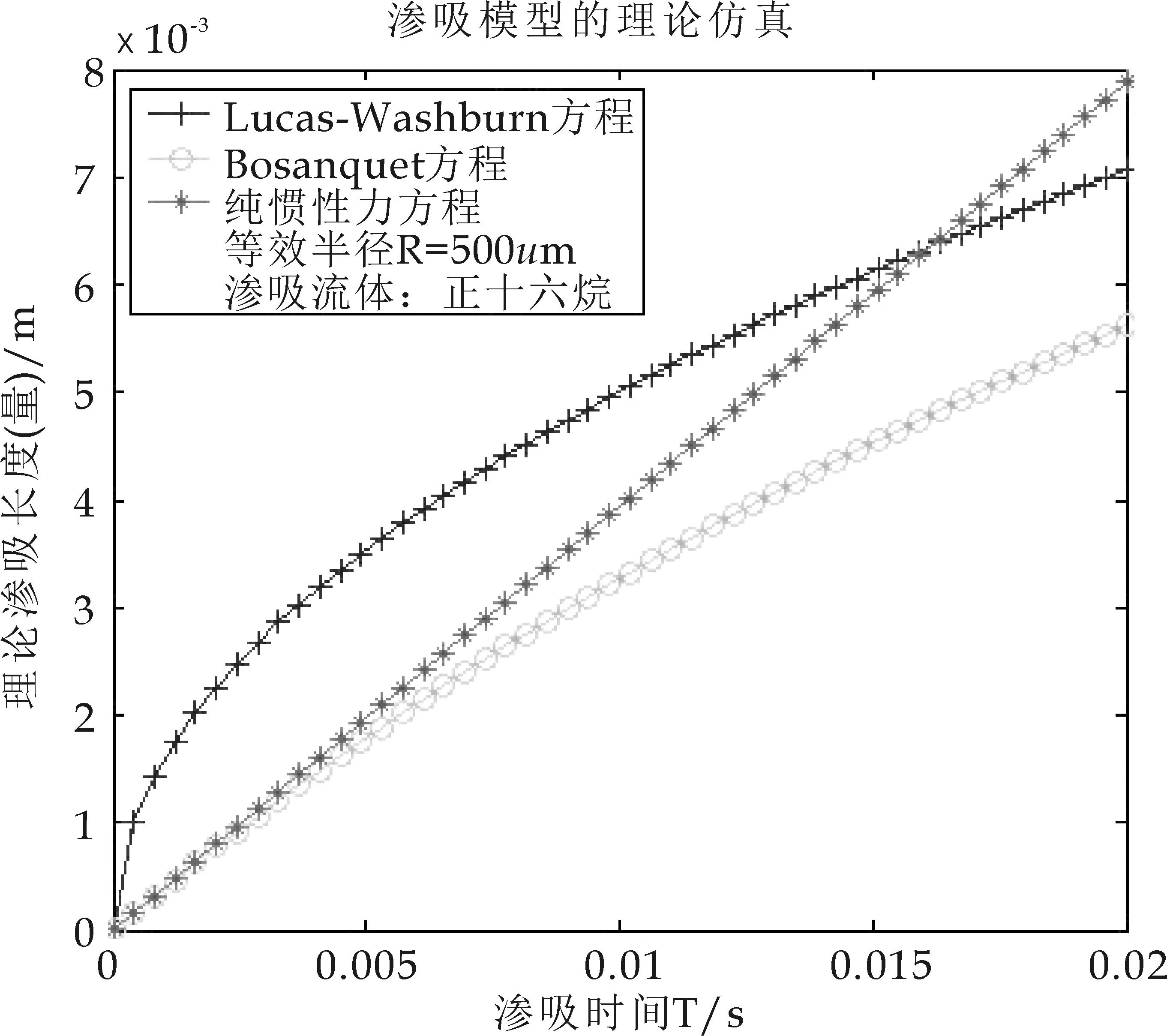
图7　渗吸初期对比图(正十六烷，R=500 μm)

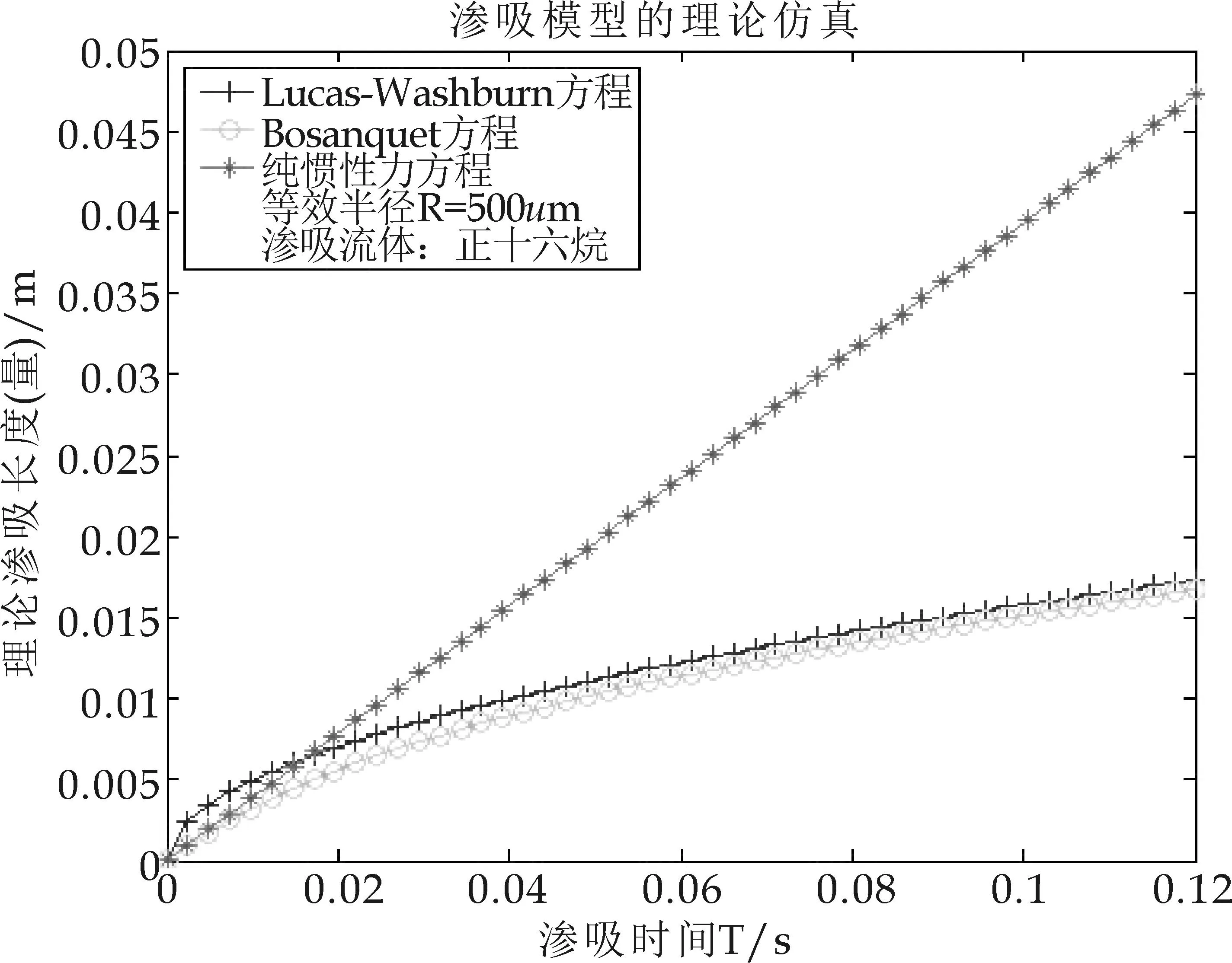
图8　渗吸后期对比图(正十六烷，R=500 μm)

(3)毛细管等效半径R=1 mm时的渗吸模型仿真结果见图9～12.

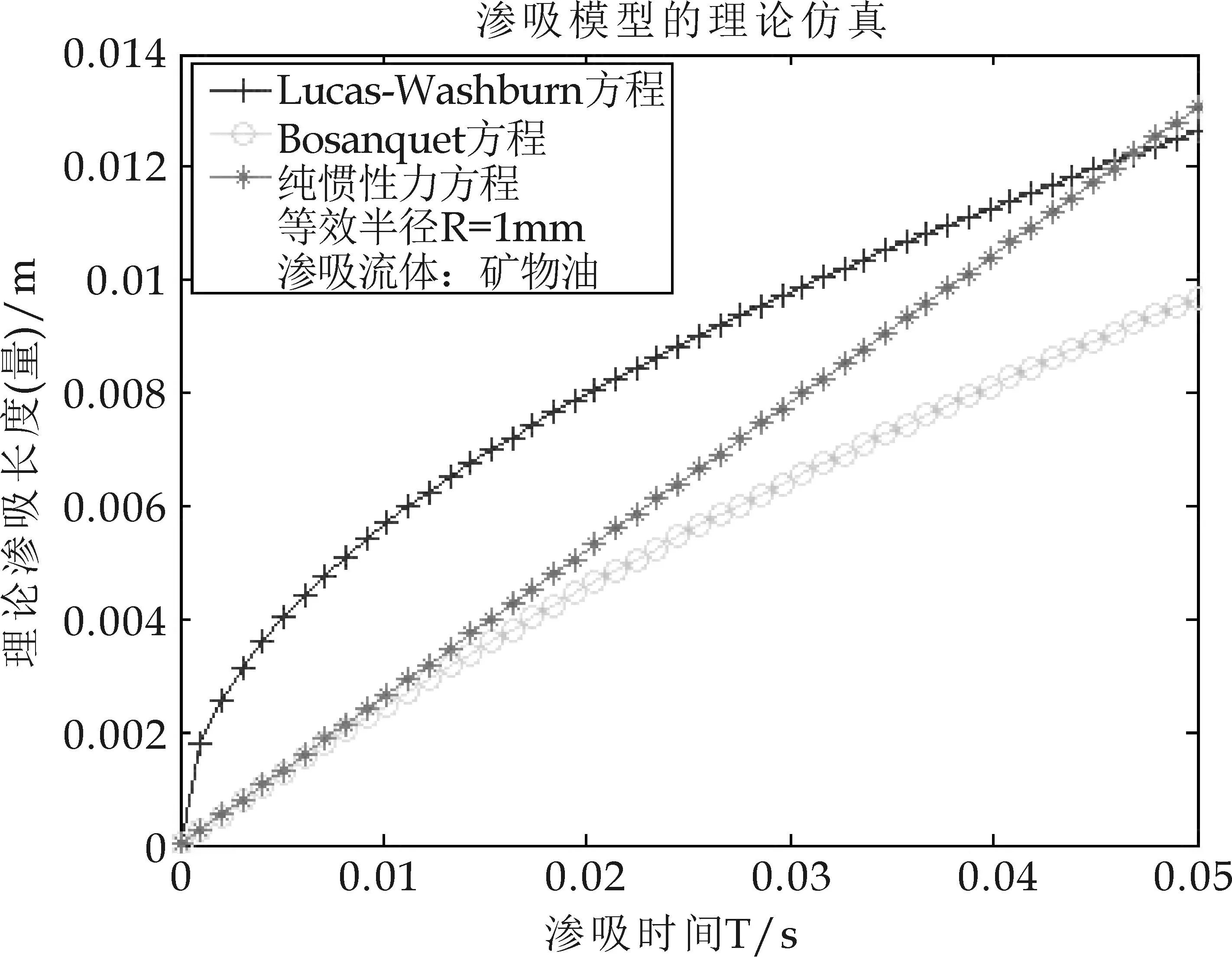
图9　渗吸初期对比图(矿物油，R=1 mm)

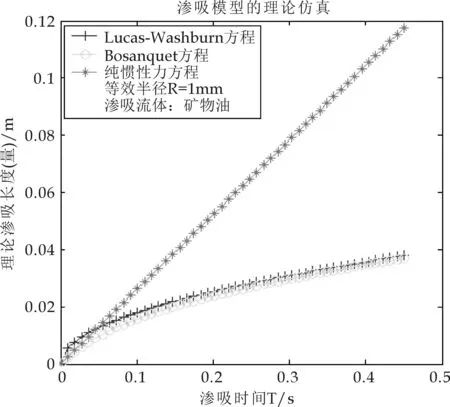
图10　渗吸后期对比图(矿物油，R=1 mm)

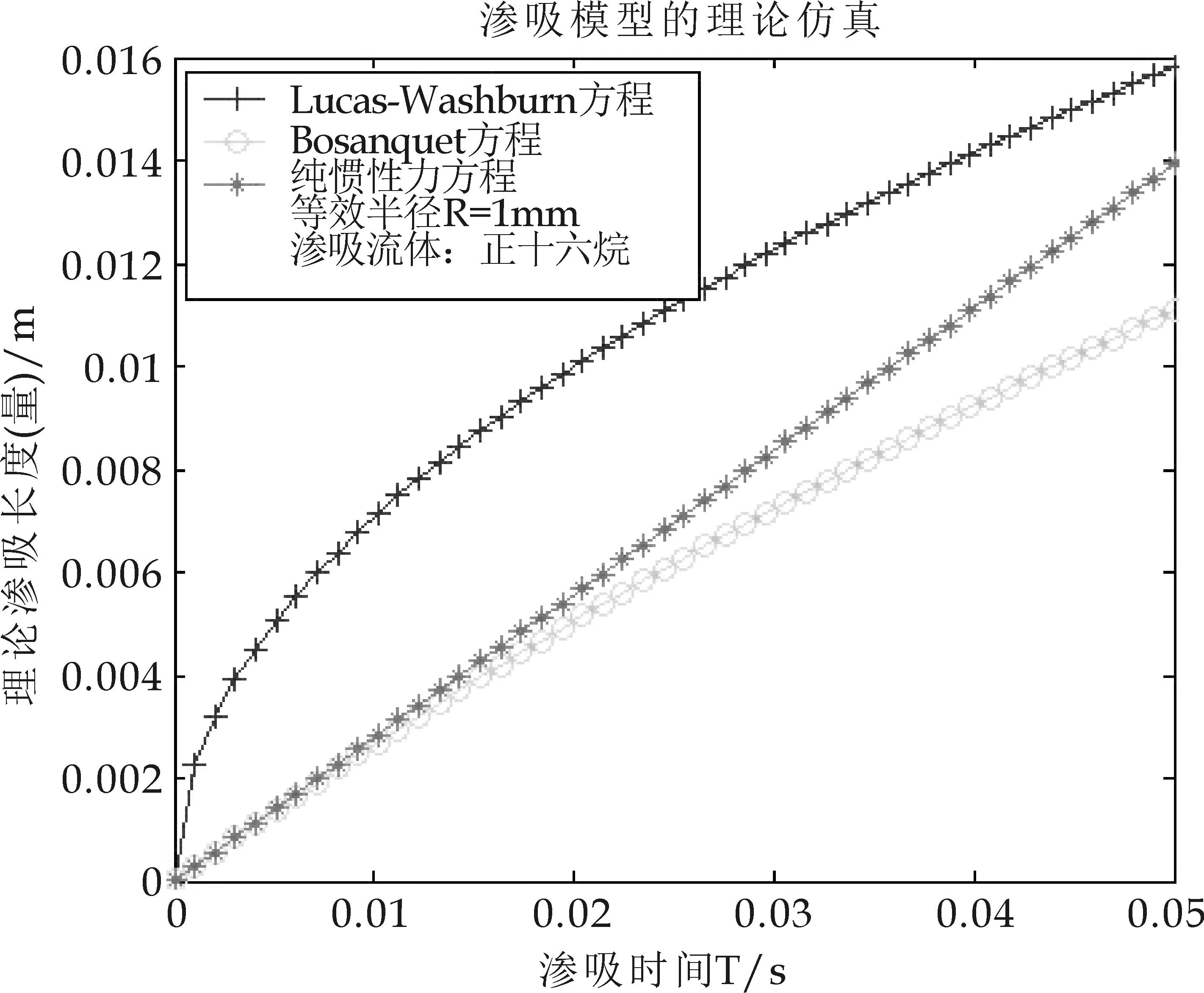
图11　渗吸初期对比图(正十六烷，R=1 mm)

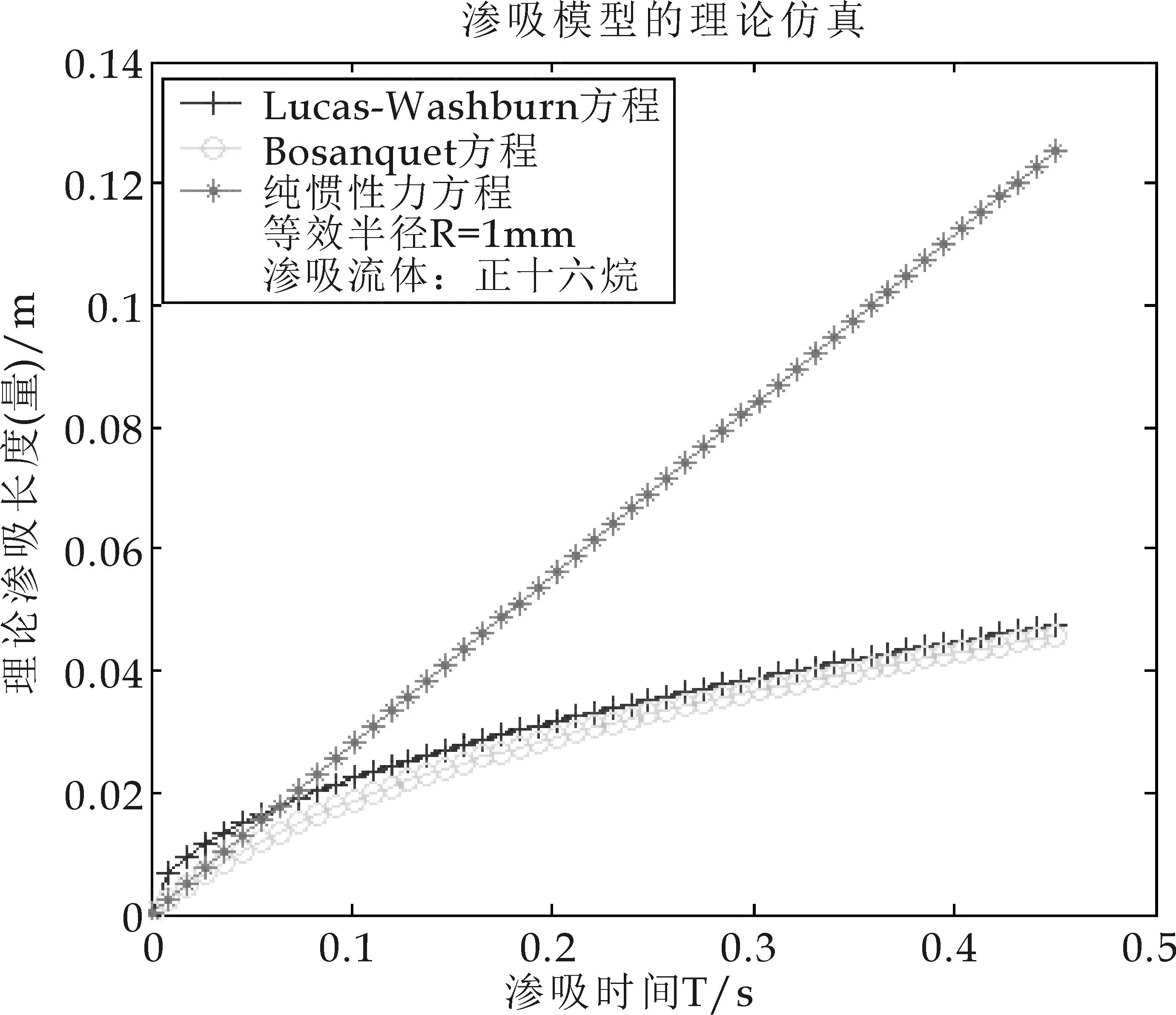
图12　渗吸后期对比图(正十六烷，R=1 mm)

从图1到图12可以看出，三种不同力学系统支配下建立的渗吸模型，的确存在着一定相互关系.在渗吸的初期阶段，当R=1μm且渗吸流体为矿物油时，Bosanquet渗吸机制与纯惯性力渗吸是重合的(如图1所示)，说明了在Bosanquet渗吸模型的初期，发生了纯惯性力支配的渗吸行为，其模型力学系统中流体的粘性力并没有起到实际的作用.同时也说明了该阶段渗吸量(渗吸体积或者渗吸高度)与渗吸时间标度是线性变化的.

随着渗吸的进一步发生，发现Bosanquet渗吸行为又与Lucas-Washburn渗吸重合的(图2).说明了随着渗吸的进行，Bosanquet渗吸模型中所强调的惯性力被消散，Bosanquet渗吸逐渐转化成以毛细力和粘性力支配的Lucas-Washburn渗吸，也说明了Bosanquet渗吸模型的后期，惯性力没有起到实际的作用，是可以被忽略的.也说明了本文第二部分推导中，Bosanquet方程和Lucas-Washburn方程等效时，是发生在渗吸的后期阶段.

当R=500μm和1 mm时，渗吸情况的具体表现跟R=1μm时完全相同，证明了渗吸初期惯性力起到的积极作用；随着渗吸的进行，渗吸支配力也慢慢过渡到毛细力和粘性力为主的力学系统中.对于渗吸流体正十六烷，获得的渗吸仿真结果也同样与矿物油的结果完全一致(笔者也验证了在其他不同等效毛细管参数下模型的对比分析结果，与上述的情况及变化趋势完全一致，限于篇幅，这里不在重复罗列相关变化图表).

另外，随着毛细管直径的增大(由1μm到500μm，再到1 mm)，Bosanquet机制阶段与纯惯性力的重合时间会逐渐增加或者延长，对于矿物油而言，重合的时间终点分别为0.8×10-8s，0.004 s，0.012 s；对于正十六烷重合的时间终点分别为1.4×10-8s，0.005 s，0.015 s.即随着纸张介质的等效毛细管半径越大，Bosanquet机制与纯惯性力机制所描述渗吸过程的一致性越长.

对于渗吸的后期阶段，Bosanquet机制阶段和Lucas-Washburn渗吸阶段重合时间也会随着等效毛细管直径的增大而渐渐推迟，即纸张介质的等效毛细管半径越小，Bosanquet渗吸与Lucas-Washburn渗吸重合的时间越早，渗吸过程的一致性越长.

纵观整个仿真结果，从另外一个方面也说明了，Bosanquet渗吸机制包括了纯惯性力阶段和Lucas-Washburn渗吸行为.另外，当等效毛细管的直径越小时，纯惯性力阶段在渗吸过程中的作用就越短.对于特定的等效毛细管直径，纯惯性力的渗吸就可以忽略不计，这也是有时在特定的材料和实验条件下，Lucas-Washburn渗吸能达到与实验结果比较匹配的重要原因之一.

4结论

通过模型的相互关系的数学推导和仿真分析可以看出，虽然经典的纯惯性力渗吸模型、Bosanquet渗吸模型及Lucas-Washburn渗吸模型，是基于不同的毛细力学支配系统建立的，但是，他们在一定物理情形下，存在着确定的相关关系.

(1)Bosanquet渗吸模型包括了纯惯性力阶段的渗吸行为和Lucas-Washburn渗吸行为，即纯惯性力渗吸和Lucas-Washburn渗吸是Bosanquet描述渗吸过程的两个特殊阶段，他们分别描述了在Bosanquet渗吸机制下渗吸的初始和后期渗吸的两个重要阶段.

(2)当纸张介质的等效毛细管半径大时，Bosanquet机制与纯惯性力机制所描述渗吸过程的一致性越长，在强调初期渗吸的情况下，表达形式简单的纯惯性力渗吸模型可以代替复杂Bosanquet渗吸模型.

(3)当纸张介质的等效毛细管半径小时，Bosanquet渗吸与Lucas-Washburn渗吸重合的时间越早，渗吸过程的一致性越长，在忽略短暂惯性效应的情况下，表达形式简单的Lucas-Washburn渗吸可以代替复杂Bosanquet渗吸模型.

(4)当需要描述整个阶段的渗吸时，Bosanquet渗吸是三种模型中最佳的表征方案.Bosanquet渗吸完整的包括了渗吸过程存在的惯性力、毛细力和粘性力，但是由于Bosanquet渗吸模型的表达式及求解过程较其他模型复杂得多，一定程度上限制了该模型的实际应用.

参考文献

[1] Li Y.,He B.Characterization of ink pigment penetration and distribution related to surface topography of paper using confocal laser scanning microscopy[J].BioResources,2011,6(3):2 690-2 702.

[2] Schoelkopf J.,Gane P.,Ridgway C.,et al.Imbibition behaviour of offset inks:I gravimetric determination of oil imbibition rate into pigmented coating structures[J].Tappi Journal,2003,2(6):9-13.

[3] 蔡建超，郁伯铭．多孔介质自发渗吸研究进展[J].力学进展,2012，42(6)：735-753．

[4] Washburn E.W.The dynamics of fluid flow[J].Phys.Rev.,1921,17:273-283.

[5] Bosanquet C.H.On the flow of liquids into capillary tubes[J].Philos.Mag,1923,45(267):525-531.

[6] Szekely J.,Neumann A.W.,Chuang Y.K.The rate of capillary penetraion and the applicability of the washburn equation[J].J.Colloid Interface Sci.,1971,35(2):273-278.

[7] Quere D. Inertial capillarity[J].Europhys Lett.,1997,39(5):533-538.

[8] Schoelkopf J.,Gane P.,Ridgway C.,et al.Practical observation of deviation from Lucas-washburn scaling in porous media[J].Colloid Surf.A.Physicochem.Eng.Asp.,2002,206:445-454.

[9] Ridgway C.J.,Gane P.A.C.,Schoelkopf J.Modified calcium carbonate coatings with rapid absorption and extensive liquid uptake capacity[J].Colloid Surf.A.Physicochem.Eng.Asp.,2004,236:91-102.

[10] Quere D.Wetting and roughness[J].Annu.Rev.Mater.Res.，2008,38:71-99.

[11] 刘国栋．造纸涂层材料自渗吸行为机制及理论建模研究[D]．西安：陕西科技大学，2014.

[12] Liu G.,Zhang M.,Ridgway C.,et al.Pore wall rugosity:The role of extended wetting contact line length during spontaneous liquid imbibition in porous media[J].Colloid Surf.A.Physicochem.Eng.Asp.,2014,443:286-295.

[13] Poulin N.,Tangup P.A.Numerical and physical modeling of the permeability of paper to CMC and coating liquids[J].The Canadian Journal of Chemical Engineering,1997,75:949-955.

[14] Liu G.,Zhang M.,Ridgway C.,et al.Spontaneous inertial lmbibition in porous media using a fractal representation of pore wall rugosity[J].Transp Porous Med,2014,104(1):231-251.

[15] Schoelkopf J.,Gane P.A.C.,Ridgway C.J.,et al, Influence of inertia on liquid absorption into paper coating structures[J].Nordic Pulp and Paper Research J.,2000,15(5):422-430.

[16] E.Chibowski,L.Holysz.On the use of Washburn′s equation for contact angle determination[J].J.Adhes.Sci.Technol.,1997,11(10):1 289-1 301.

【责任编辑：蒋亚儒】

The exploration of interaction relationship of classical imbibition models of paper-based media

LIU Guo-dong1, CHENG Nan-nan1, WANG Yue2， MA Xin1, WANG Zhe1

(1.College of Light Industry and Energy, Shaanxi Province Key Laboratory of Papermaking Technology and Specialty Paper, Shaanxi University of Science & Technology, Xi′an 710021, China; 2.Shaanxi Youth Vocational College, Xi′an 710068, China )

Abstract:Aiming at the different imbibition models of inertial,Bosanquet and Lucas-Washburn when charactering the imbibition process of paper-based materials.The interaction relationship between these models is discovered by means of specific imbibition analysis and theoretical mathematic method based on the uniform physical parameters and conditions. On the basis of the imbibition analysis of these models,the specific and reasonable application situations are discussed further eventually,which can provide the theoretical evidences to describe the imbibition performance of paper-based media.

Key words:inertial imbibition model； Bosanquet imbibition model； Lucas-Washburn imbibition model

中图分类号：TS727+.3

文献标志码：A

文章编号：1000-5811(2016)02-0035-06

作者简介:刘国栋(1981-)，男，陕西乾县人，副教授，博士，研究方向：印刷油墨流体与纸张相互作用的关系

基金项目：国家自然科学基金项目(51402180); 陕西省教育厅专项科研计划项目(14JK1108); 陕西省协同创新计划项目(2015XT-64); 陕西省留学人员科技活动项目([2014]1059);国家级大学生创新创业训练计划项目(201510708143) ; 陕西科技大学博士科研启动基金项目( BJ15-11)

收稿日期:2015-12-01