基于多核融合的中文领域实体关系抽取

郭剑毅,陈 鹏,余正涛, 线岩团, 毛存礼, 赵 君

(1. 昆明理工大学 信息工程与自动化学院，云南 昆明 650500; 2. 昆明理工大学 智能信息处理重点实验室，云南 昆明 650500)

基于多核融合的中文领域实体关系抽取

郭剑毅1,2,陈 鹏1,余正涛1,2, 线岩团1,2, 毛存礼1,2, 赵 君1

(1. 昆明理工大学 信息工程与自动化学院，云南 昆明 650500; 2. 昆明理工大学 智能信息处理重点实验室，云南 昆明 650500)

针对传统径向基核函数的训练矩阵中所有元素都十分接近零而不利于分类的问题，该文提出了一种融合了改进的径向基核函数及其他核函数的多核融合中文领域实体关系抽取方法。利用径向基核函数的数学特性，提出一种改进的训练矩阵，使训练矩阵中的向量离散化，并以此改进的径向基核函数融合多项式核函数及卷积树核函数，通过枚举的方式寻找最优的复合核函数参数，并以上述多核融合方法与支持向量机结合进行中文领域实体关系抽取。在旅游领域的语料上测试，相对于单一核方法及传统多核融合方法，关系抽取性能得到提高。

关系抽取;径向基核函数;卷积核函数;多核融合

1 前言

中文领域实体关系抽取即从多样化的中文领域文本中找出实体对之间的关系，是自然语言处理的基础，为中文领域信息检索、自动问答系统、机器翻译、本体构建等提供重要技术支持。

目前中文领域关系抽取的基于机器学习方法主要包括基于特征向量[1-2]的方法、基于卷积核函数[3-5]及多核融合[6-8]的方法。基于特征向量的机器学习方法通过构造分类器来进行关系分类，虽然运算速度快，但是仅利用平面核函数表达文本的平面信息因为不能有效挖掘文本的结构信息，使抽取性能遇到了瓶颈。利用卷积核函数替代平面核函数计算两个对象的相似度，在充分挖掘句法信息或依存信息等文本结构信息方面具有一定的潜力，因此卷积核函数方法应用在中文领域实体关系抽取上取得了一定的发展。Yu等[3]为了增加句法树包含的信息，提出基于卷积树核函数的中文实体语义关系抽取方法，构造能有效捕获结构化信息和实体语义信息的合一句法和实体语义关系树，从而提高了中文语义关系抽取的性能；Liu等[5]在原有关系实例的最短路径包含树的基础上，利用Hownet加入语义信息，从而提高中文关系抽取性能。但是仅使用单一的卷积核方法忽略了文本的平面信息具有局限性。多核融合的方法兼顾了文本的平面信息及结构信息的优点，目前在关系抽取领域取得了很好的效果；Huang等[6]提出了一种卷积树核分别与线性核及多项式核融合的多核融合方法，表明多核融合能有效提高关系抽取的性能；文献[7]证明，在多核融合的过程中，提高单一核函数在关系抽取中的性能能够提高复合核函数在关系抽取中的性能。由于传统的径向基核函数在形成训练矩阵时，训练矩阵中的所有元素趋近于0而导致分类模型分类效果不佳，使得融合了径向基核函数的复合核函数的中文领域关系抽取性能下降。

针对上述问题，本文以中文旅游领域为对象，根据径向基函数的数学特征，改造径向基核函数训练矩阵，以解决传统径向基核函数训练矩阵的元素趋近于0而不利于分类的问题，融合了多项式核函数及卷积树核函数，试图提高中文领域关系抽取的性能。实验结果表明，在中文旅游领域语料下，采用本文提出的模型进行关系抽取，其准确率、召回率和F值均优于单一核函数方法及单一平面核函数与树核函数融合的方法。

2 基于多核融合的领域实体关系抽取

2.1 改进的复合平面核函数

2.1.1 核函数训练矩阵

对于平面特征向量形成的特征矩阵，在被某种映射规则映射后形成的矩阵即为核函数训练矩阵，训练矩阵是一个半正定对称矩阵。假设有特征向量X1,X2,…Xm，i,j∈{1,2,…，m}。有映射φ(X)，且φ(X)的点积K(Xi,Xj)为合法的核函数。则它们经过映射φ 形成的训练矩阵：

在之后的分类过程中，核函数矩阵是唯一能被运用的信息。也就是说，核函数训练矩阵质量的好坏决定了分类的好坏，从而影响关系抽取的质量。

2.1.2 改进的径向基训练矩阵

径向基核函数是一种平移不变核函数，具体表达式为式(1)所示。

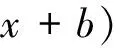
(1)

在系数a=1,b=0下，径向基函数如图1所示。由图1可以看出，随着x增加，函数值极其迅速的接近于0。

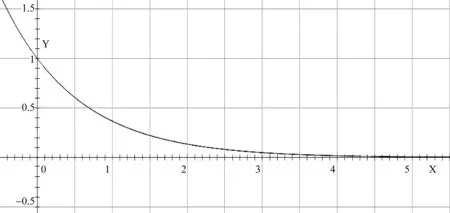
图1 径向基函数曲线图

对于任意两个特征向量Xi,Xj,i,j∈{1,2,…，m}，它们的映射构成新的映射空间中第i个向量的第j个特征，而由于径向基核函数的数学性质，使得每一个元素都十分趋近于0，这是十分不利于进行分类工作的。例如，有三个二维向量a,b,c分别为：a=(2,3)，b=(4,10)，c=(3,5)，它们映射到径向基核函数对应的空间的训练矩阵为：

为了解决上述问题，本文采用将训练矩阵中每一个特征都限制在一个适当的范围内，而便于进行分类工作。例如，将范围限制在0.2～1之间，改进训练矩阵的方法为：

1) 计算Featureij=‖Xi-Xj‖2，其中,i,j∈{1,2,…，m}；

2) 枚举所有的Featureij，找到最大值，记为Featuremax；

3) 计算常数δ=(-ln0.2)/Featuremax；

4) 规范化后的训练矩阵即:Knew=[k(Featureij×δ)]m×m。

其中i,j∈1,2,…，m。将上述三个向量a,b,c规范化处理后的训练矩阵为：

2.1.3 基于径向基与多项式复合平面核函数

由于大部分平面核函数都可以由内积核及平移不变核表示，而不同的核函数空间分类效果也不同。为了融合内积核函数及平面核函数的特性，本文选择多项式核函数及改进的径向基核函数的线性复合平面核函数表达平面信息。定义如式(2)所示。

CPK(V1,V2)=βRBF(V1,V2)+

(2)

其中CPK(V1,V2)为复合平面核函数，RBF(V1,V2)为径向基核函数，PK(V1,V2)为多项式核函数，β为复合平面核函数权重参数，Vi为任意实例的特征向量。

本文特征集选择了中文领域实体关系抽取中成熟的特征[1-2,6-7]。特征选择如下：实体类型、实体对的组合类型、实体词性及上下文词性(窗口为2)[1]、实体对距离、实体对间出现其他实体的个数、实体对间语义词汇。结合以上特征选择，将实例向量化，形成特征矩阵。当获取了复合平面核函数矩阵集后，将遍历训练其中所有复合平面核函数，获取不同核函数对应的分类器，分别考察分类器的抽取性能，以确定最优复合平面核函数。

2.2 融合语义信息的卷积树构造

本文采用Collins和Duffy[9]的卷积树核函数(ConvolutionTreeKernel，CTK)，即两棵树之间的相似度可以通过计算它们之间的相同子树的数目来实现，表示为公式(3)。

(3)

其中N1和N2分别为T1和T2的节点集合，Δ(n1,n2)用来计算以n1和n2为根节点的两颗子树之间的相似度。

2.2.1 基于句法树的实例表示方式

卷积树核函数计算的对象为两个子树，在实体语义关系抽取中，关系实例的表达方式有多种。一个完全句法树结构过于复杂，包含了大量的噪声信息，因此基于完全句法树的实例的关系抽取效果不理想，因此通常需要对句法树进行裁剪。Zhang[10]等在效果最好的最小完全句法树(MCT)和最短路径树(PT)的实验表明，PT树结构的实验结果最好。故本文采用PT树为基础融合语义信息。

2.2.2 基于句法树和语义树的集成树

在句法树结构中，并不包含实例的语义信息，如：实体大类类型、实体子类类型和实体引用类型等。文献[3，11]探讨了语义信息加入到句法树中对关系抽取性能的影响，加入语义信息后的树能够同时包含结构化及平面化的信息，从而有更好的抽取性能。所以，本文对句法树进行改造加入语义信息。根据已有的研究，本文以特征匹配树(FTP)为添加方式，将语义信息直接挂在根节点上，加入实体大类，实体小类及引用类型三种语义信息。

集成树构造的具体过程为：首先将同一个关系中的两个实体的同一特征先挂到父节点上，然后再统一挂到根节点上。例如，“TP1”和“TP2”先挂到父节点“TP”上，然后再同其他特征节点挂到根节点上，如图2所示。

图2 集成树的关系实例

2.3 基于平面核及卷积核的复合核函数

根据已定义的卷积树核CTK和复合平面核函数CPK，定义复合核函数如式(4)所示。

CK(R1,R2)=αCTK(T1,T2)+

(4)

其中，CK(R1，R2)表示两个实例R1、R2之间的相似度；CPK(V1,V2) 表示两个实例R1和R2的两个特征向量V1和V2的相似度，可由复合平面核计算得到；CTK(T1,T2)是由卷积树核计算得到两棵子树的相似度，T1和T2是从两个候选关系实例的分析树中抽取出来的子树。 @ 是复合核函数权重参数。

3 实验设计与结果分析

相对于其他机器学习算法，支持向量机在实体关系抽取领域通用性较好，分类精度高，且分类速度只与支持向量数目而不是所有的训练样本数目有关，所以本文选择支持向量机训练数据，本文的实验工具使用Tree Toolkits*http://disi.unitn.it/moschitti/Tree-Kernel.htm。本文使用的语料为人工从互联网及文献资料中获取的中文旅游文本共600余篇，预处理后包括正例1 023个，负例5 450个。在训练中使用十倍交叉验证以最大化利用数据,实验评测采用自然语言处理的通常使用的标准：准确率、召回率、F值, F值评测系统的最终性能。

3.1 实验设计

为了验证本文方法的有效性，并与其他传统方法进行比较，本文设计了四项任务。

任务1，验证改进的径向基核函数对关系抽取性能的影响。由于径向基函数的特性，在函数值为0.1后函数趋近为0的趋势很快，所以设定规范的范围分别为0～1，0.1～1，0.2～1，0.3～1四组范围；任务2，验证复合平面核函数对抽取性能的影响与平面核树及树核形成的复合核对抽取性能的影响成正比。实验用枚举的方法探索权重参数β对复合平面核抽取性能的影响；任务3，利用枚举的方法寻找树核函数及复合平面核函数在融合形成的复合核函数中占什么比例，使得抽取性能最优；任务4，验证本文提出系统的有效性。用任务3找到的最优比例的多核融合的复合核核函数与特征向量方法，单一核方法及其他多核融合系统进行比较。

3.2 实验结果及分析

3.2.1 验证改进的径向基训练矩阵对抽取性能的影响

由表1可以看出，系统经过训练矩阵规范化处理后，准确率和召回率都有较大的提高，但是并不是随着取值范围的最小值增加系统的F值就增加。说明规范范围缩小到一定程度后，系统分类效果降低。在0.2～1这个范围内系统F值最高，本文以后的实验中，径向基核函数的训练矩阵都以这个范围规范。

表1 不同训练矩阵下的RBF抽取性能

3.2.2 寻找复合平面核函数的最优比例

实验中设置权重参数 β上下限为0～1，步长为0.1。特别的，在不考虑 α 的情况下，当 β为0时，平面核函数只包括多项式函数的特性；当 β为1时，平面核函数只包括径向基核函数的特性。由于只考虑权重参数 β对抽取性能的影响，这里假设 α 为0.5。

表2 不同权重参数 β下多核融合核函数的抽取性能

从表2可以看出，对于旅游领域，当权重参数 β 为0.1时，性能是最好的，并且召回率对于权重参数 β并不十分敏感。

3.2.3 寻找平面核与树核融合的最优比例

从表3可以看出，对于旅游领域，当权重参数 α 为0.3α1=0.1时，抽取性能是最好的，说明平面核函数对多核融合核函数抽取性能的贡献要更多一些。

表3 不同权重参数α下多核融合核函数的抽取性能

3.2.4 总体性能与其他同类系统的比较

表4 与其他同类系统的比较

在表(4)这一组实验中可以看出：(1)无论是复合平面核函数还是树核函数，其性能都没有两种核函数融合的复合核函数抽取性能好；(2)与树核与单一核函数的复合核函数比较，当提高了平面核函数性能后，整体关系抽取性能有所增加。

4 结束语

本文以支持向量机为机器学习算法，通过改进的径向基核与多项式核及卷积树核融合得到多核融合核函数，进行中文领域实体关系抽取。在中文旅游领域中，本文提出的多核融合系统取得了66.69%的F值，与单一核及其他平面核与树核的复合核函数相比，抽取性能有所提高。下一步工作中，将尝试以下两种途径以期待抽取性能的提高：

(1) 融入多样化的核函数以提高抽取能力；

(2) 提高单一核函数的抽取能力以提高整体抽取能力。

[1] 车万翔, 刘挺, 李生. 实体关系自动抽取[J]. 中文信息学报, 2005, 19(2):1-6.

[2] Lei Chunya, Guo Jianyi, Yu Zhentao, et al. The Field of Automatic Entity Relation Extraction based on Binary Classifier and Reasoning[C]//Proceedings of the Third International Symposium on Information Processing. Qingdao, China, 2010:327-2-331.

[3] 虞欢欢，钱龙华，周国栋，等.基于合一句法和实体语义树的中文语义关系抽取[J]，中文信息学报，2010,24(5):17-23.

[4] Peng Cheng, Gu Jinghang, Qian Longhua. Research on Tree Kernel-Based Personal Relation Extraction[J]. Communications in Computer and Information Science,2012, 333:225-236.

[5] Liu Dandan, Zhao Zhiwei, Hu yanan, et al. Incorporating Lexical Semantic Similarity to Tree Kernel-based Chinese Relatin Extraction[J]. Lecture Notes in Computer Science, 2013, 7717: 11-21.

[6] 黄瑞红，孙乐，冯元勇，等.基于核方法的中文实体关系抽取研究[J].中文信息学报，2008,22(5):102-108.

[7] Zhang Ji, Ouyang You, Li Wenjie, et al. A Novel Composite Kernel Approach to Chinese Entity Relation Extraction[J]. Lecture Notes in Computer Science, 2009, 5459:236-247.

[8] Li Haiguang, Wu Xindong, Li Zhao, et al. A relation extraction method of Chinese named entities based on location and semantic features[J].Applied Intelligence, 2013, 18(1): 1-15.

[9] Collins M, Duffy N. Covolution kernels for natural language[C]//Proceedings of the NIPS′2001. Cambridge, MA 2001: 625-632．

[10] Zhang Ming, Zhang Jie, Su Jian, et al. A Composite Kernel to Extract Relations between Entities with both Flat and Structured Features[C]//Proceedings of the COLING-ACL′2006．Sydney, Australia, 2006: 825-832.

[11] Qian Longhua,Zhou Guodong,Zhu Qiaoming. Exploiting constituent dependencies for tree kernel-based semantic relation extraction[C]//Proceedings of the COLING′2008. Manchester, UK, 2008: 697-704.

Domain Specific Chinese Semantic Relation Extraction Based on Composite Kernel

GUO Jianyi1,2, CHEN Peng1, YU Zhengtao1,2, XIAN Yantuan1,2, MAO Cunli1,2, ZHAO Jun1

(1. The School of Information Engineering and Automation, Kunming University of Science and Technology, Kunming, Yunnan 650500, China; 2. Key Laboratory of Intelligent Information Processing, Kunming University of Science and Technology, Kunming, Yunnan 650500,China)

This paper proposes a composite kernel approach to Chinese semantic relation extraction by a composite kernel. This paper designs an improved training matrix by using the mathematical properties of radial basis kernel in order to make vectors disperse in the training matrix, then integrate this kernel with the polynomial kernel and the convolution tree kernel. It enumerates for the best parameters of the composite kernel function for Chinese semantic relation extraction. Experimented on the tourist domain texts, the porposed method out-performs methods of single kernel as well as a traditional composite kernel.

relation extraction; radial basis kernel function; convolution kernel; composite kernel

郭剑毅(1964—)，通信作者，硕士生导师，教授，主要研究领域为自然语言处理、信息抽取、机器学习等。E⁃mail：gjade86@hotmail．com陈鹏(1987—)，硕士研究生，主要研究领域为实体关系抽取。E⁃mail：chen．peng0905@163．com余正涛(1970—)，教授，博士生导师，主要研究领域为自然语言处理、信息检索、机器翻译、机器学习等。E⁃mail：ztyu@hotmail．com

1003-0077(2016)01-0024-06

2013-07-10 定稿日期： 2014-05-10

国家自然科学基金(61175068,61562052)

TP391

A