基于离散元数值模拟的应变分析和裂缝预测技术

蔡申阳，尹宏伟*,李长圣，贾东，汪伟，陈竹新，魏东涛.南京大学能源科学研究院，地球科学与工程学院，南京00；.中国石油勘探开发研究院，北京0008；.中国石油勘探开发研究院西北分院，兰州700



基于离散元数值模拟的应变分析和裂缝预测技术

蔡申阳1，尹宏伟1*,李长圣1，贾东1，汪伟1，陈竹新2，魏东涛3
1.南京大学能源科学研究院，地球科学与工程学院，南京210023；2.中国石油勘探开发研究院，北京100083；3.中国石油勘探开发研究院西北分院，兰州730022

摘要：应变分析与裂缝预测技术在地学领域具有重要应用意义。离散元方法虽然能有效分析含有大量间断的问题，但目前在地学领域应用较少。文中尝试使用离散元方法表示符合实际性质的岩石，模拟水平挤压环境下滑脱构造的形成过程，并对变形过程中的应变分布变化与裂缝生成规律进行了分析。结果表明：在挤压环境的滑脱构造中，裂缝产生的高峰期先于断层明显活动期，局部区域内聚集的大量裂缝是产生断层的诱因；已经出现明显活动的断层中产生的裂缝较少。裂缝集中区域和应变集中区域相互重叠，裂缝越发育则应变越强烈。受同一个断层影响的裂缝首先在断面上集中出现，随后产生在断面周边区域；在受断层影响的范围内，裂缝距离断面越远则形成时间越晚。该成果还表明离散元方法在应变分析与裂缝预测研究中具有巨大潜力。

关键词：离散元方法；应变分析；裂缝预测

地体应变分析及裂缝预测技术在地学有关生产研究领域具有重要意义。例如，何雨单和魏春光（2007）认为裂缝型油气藏蕴含着巨大的调整和挖掘潜力，而还原构造应力场是预测裂缝型油藏的重要手段之一；龙鹏宇等（2011）指出页岩气有利勘探目标区应首选那些拥有较高渗透能力或具备可改造条件的泥页岩裂缝发育带；聂海宽等（2009）论证了裂缝的规模对页岩气开采有双重影响，适量的裂缝可以提高页岩总含气量，而过多裂缝则可能导致天然气大量散失，因此页岩气出产最佳区域需要深度、温度、有机碳含量和裂缝等因素的良好匹配。Gale等（2007）曾分析了美国Barnett页岩的应力场和天然裂缝分布，并提出大型开放式裂缝的稀疏分布可能不利于水力压裂开采。此外，Lee和Dan（2005）还研究了包括构造裂缝在内的诸多滑坡诱发因素，并在此基础上建立了概率模型，预测准确度达到了83.47%，表明研究天然裂缝有助于了解滑坡产生的机制。

目前，通过物理手段预测构造裂缝的方式已较为完善。研究者利用光弹模拟物理实验还原古构造应力场来预测裂缝的走向与类型（Yin and Zhang，2007；单家增等，2005；马寅生等，2002）；Abdelmalak等（2012）将沙箱模拟实验与粒子成像测速（PIV）方法相结合，建立二维模型，并分析了两种不同岩浆侵入方式导致的地表破裂变形形态差异。近年来，数值模拟也被广泛用于构造应力应变分析和裂缝预测中，文世鹏和李德同（1996）给出了构造裂缝定量预测的有限元数值模拟技术基本原理和方法，（陈波和田崇鲁，1998）则举出了相应的应用实例。有限元方法不能很好地解决含有大量间断或位移的问题，而离散元方法很好地解决了这项不足。离散元方法最先由Cundall 和Strack（1979）完整提出，最初主要用于研究岩块的节理破裂以及粒状物质和土壤力学问题的试验模拟中。二十世纪末，地质学家开始将其应用于剪切带问题（Iwashita and Oda,2000; Saltzer and Pollard，1992），断层及断层相关褶皱的研究等地质构造问题的研究中（Finch et al.,2003; Hardy and Finchk,2005; Morgan,1997; Saltzer and Pollard,1992; Strayer et al.,2004; Strayer and Suppe，2002;孟令森等，2007;张洁等，2008a，2008b）。离散元方法在一定程度上突破了物理模拟存在的流变学和比例化问题。与其他连续体数值模拟方法相比，离散元方法采用颗粒相互作用来模拟系统的动力学机制，因此试验者可以对系统的运动演化进行模拟和观测。另外由于它允许颗粒间较大相对位移，可以更好地模拟高度形变，所以非常适于研究存在大量间断（如断层、节理、破裂）的问题。例如，刘泉声（2011）利用离散元方法分析裂隙岩体等效渗透系数，得出了应力比的增加使水力耦合效果更明显的结论；杨艳等（2012）采用BPM（Bonded-Parti⁃cle Model）模型很好地再现了裂隙岩体水力劈裂的形态。司马军等（2013）模拟了黏性圆形薄层土试样在粗糙边界条件下的产生及扩展过程，其裂缝参数演化规律与室内试验结果基本一致。孙萍等（2008）通过离散元分析了裂缝带错动对地铁区间隧道的影响，得出了不同错距工况下隧道衬砌的变形和应力。但是，在模拟和预测构造裂缝领域，离散元的应用仍有所欠缺。

本实验以离散元方法为基础，采用含固结力的颗粒材料，模拟挤压环境下的滑脱构造的形成过程，并通过应变计算和裂缝观测来分析裂缝生成规律，从而探索预测构造裂缝的新方法

1　离散元的原理

基于离散元方法的计算模拟一般可以概括为两部分：第一步，应用不同的力-位移法则（即本构模型，如固体晶格模型、线性接触模型等）计算颗粒间的接触力；第二步，对每个颗粒应用牛顿第二定律，更新其位置。反复执行这两个步骤，直到计算结束。本文的数值模拟是在开源离散元软件YADE（Yet Another Dynamic Engine）（Kozicki and Donz,2008,2009; Milauer et al.,2014）的框架下进行。YADE作为一个基于面向对象的离散元开源软件，易于扩展性，设计之初就考虑了与各种其他方法（如FEM）耦合，使得许多学者开始采用其做科学研究（Scholt and Donz，2013;徐文杰等,2012）。较为完美的程序框架和方便的前后处理，目的是让科学研究人员集中于真正的科学问题，而不再花费太多时间在程序接口、数据的输入输出、网格生成及可视化的编程实现上（Kozicki and Donz,2008）。

1.1本构模型

颗粒a、b相互接触时，其作用力可以分解为法向力Fn和切向力Fs，法向力Fn可通过颗粒的法向叠合量得到，切向力通过增量的形式计算得到。

颗粒间的法向力与位移的关系如图1所示，可分解为压缩和拉伸两部分。

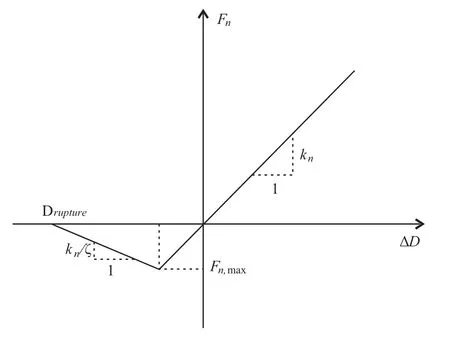
图1　颗粒间的法向力-位移关系Fig.1 Normal force-displacement relationships between particles

压缩时，Fn用下式计算：Fn= kn∆D（1）其中，∆D为颗粒a和颗粒b的叠合量，kn为法向刚度，其定义如下：

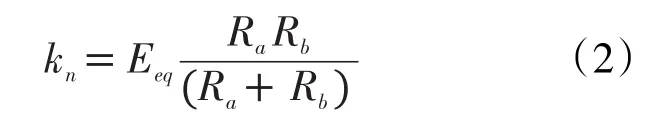
式中，Eeq为等效体积弹性模量，Ra和Rb分别为颗粒a和颗粒b的半径。

拉伸时，当拉伸距离较小时，法向力计算时的法向刚度取值与压缩时一样。两颗粒可承受最大的拉力定义为抗拉强度，用下式计算：

其中，两颗粒的接触面积Aint=πr2，这里r取Ra和Rb中的较小值。

当两颗粒间的拉力超过抗拉强度时，颗粒间的连接断裂。能量释放，需要修正法向刚度，法向力用下式计算：

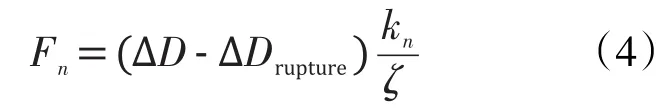
当∆D＞∆Drupture时，颗粒连接发生拉伸断裂，颗粒间的接触力（法向力和切向力）重置为零。

颗粒间的切向力以增量的形式计算，定义为（Hart et al.,1988）：

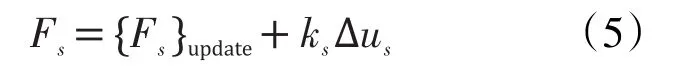
ks为切向刚度，∆us为颗粒间的切向位移增量。

颗粒间相互作用力应符合莫尔库伦法则，见图2。

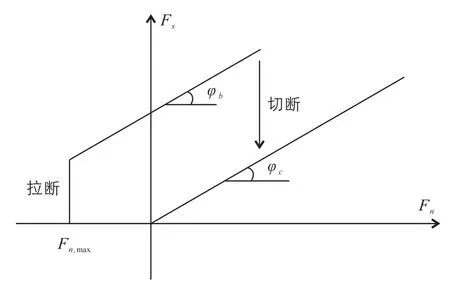
图2　颗粒连接的断裂准则Fig.2 Breaking rules of a particle bond

颗粒间的最大剪切力为：

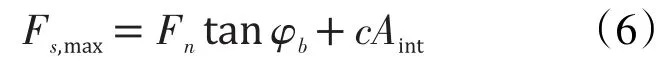
φb为内摩擦角，c为粘聚力。如果Fs＞Fs,max，颗粒间的连接断裂，进入纯滑动状态。断裂的连接（拉断或者切断）最大剪切力定义为：

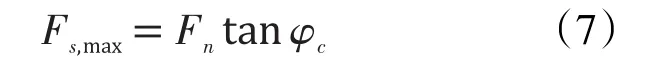
φb为连接断裂后颗粒间的内摩擦角。

另外，为了模拟准静态行为，需要给系统加入局部阻尼来耗散系统的动能（Potyondy and Cundall,2004）。

1.2初始连接的生成

一般的离散元方法（Inc,2012; Milauer et al.,2014; Shiu et al.,2008）中，只有两个颗粒真实接触时（两颗粒圆心间的距离小于两颗粒半径之和），才生成初始连接。这里重新定义初始连接生成的范围，给定一个连接生成的接触范围系数γint，不仅仅真实接触的颗粒间会建立起连接关系，在给定的范围内的其他邻居颗粒也会产生连接关系，如图3所示。

初始连接在计算开始前生成，如果两颗粒圆心间的距离小于平衡距离Deq=γint(Ra+ Rb)，则两颗粒产生初始连接（Donze et al.,1997）。这里γint取值不能太大，以防产生跨越颗粒的连接，例如当Rmax/Rmin= 2时，γint≤1.5。

为了避免颗粒间产生自锁力，公式（1）中，相对位移修正为：

可知，当γint= 1时，颗粒初始连接就是按照一般的离散元方法生成的。

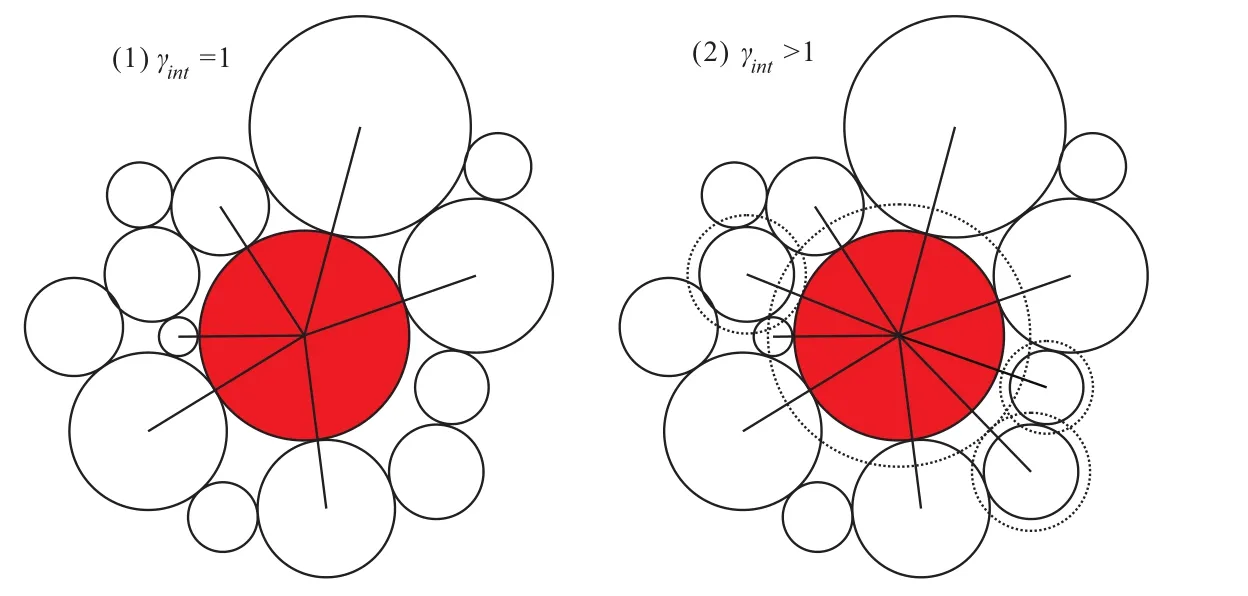
图3　接触范围系数对生成连接的影响示例Fig.3 An example of the in fluence of interaction range coefficient on bonds generation

1.3应变的计算

在离散元模型中，作为离散单元的颗粒无法变形且不可分割，因此颗粒集合体在空间上是离散的。要研究模型的宏观应变，可以采用三角剖分的方法重新构造连续体。YADE采用Delaunay方法（Catalano et al.,2014），以每个颗粒圆心作为顶点剖分整个空间，如图4所示。

通过计算剖分单元的形变，可以得到相应的应变张量，其表示形式如下：

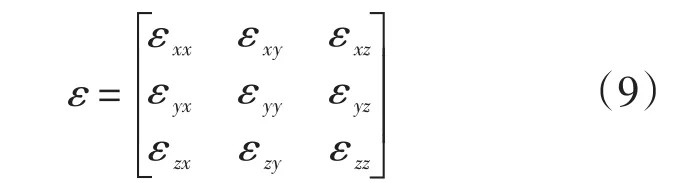
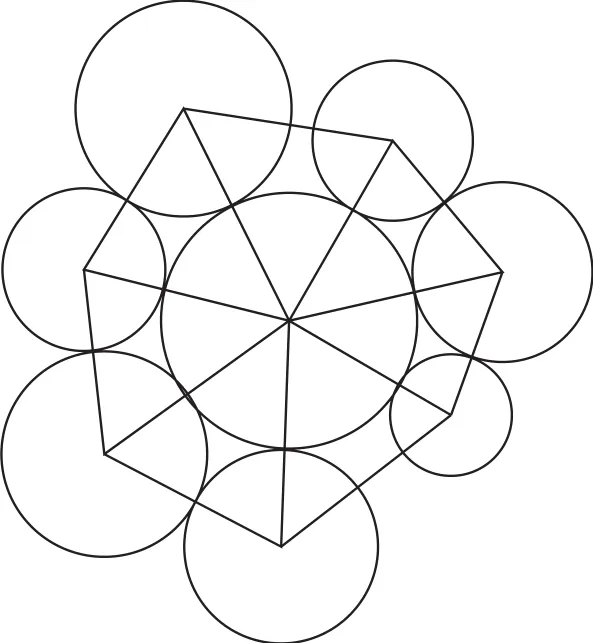
图4　Delaunay三角剖分法示例Fig.4 An example of Delaunay triangulation

剖分单元的体应变εv即为该张量的第一不变量，其值为应变张量对角线上元素的和：

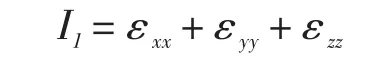
该值反映了剖分单元等比例变形的程度，负值代表压缩，正值代表膨胀，且绝对值越大说明变形程度越高。

在得到体应变的同时可以得出球应变张量：

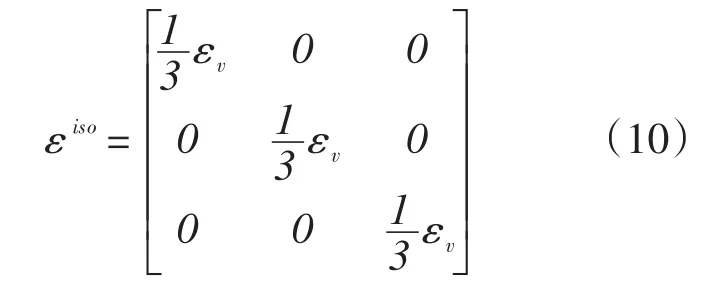
从应变张量中减去球应变张量从而得到偏应变张量：

而剖分单元的扭曲程度可以通过计算偏应变张量的第二不变量（应变偏量）得到：

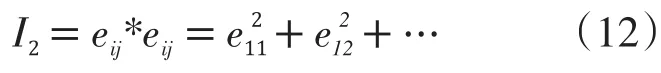
应变偏量I2没有单位，其值越大，表示剖分单元的扭曲程度越大。

2　构造数值模拟试验

2.1材料参数

在合适的参数下，离散元方法可以很好地模拟岩石的变形和断裂，但是在开始试验前需要调试微观参数，使颗粒集合体的宏观参数和实际岩石的力学性质相吻合。通过大量的模型试验和结果对比，笔者得出了一组挤压实验结果比较符合实际的模型参数，在该套参数下的模拟实验中不会出现不符合实际的滑坡或孔穴（Hughes et al.,2014）。本试验所用参数见表1，颗粒半径R均匀分布在区间内，所有颗粒的密度为4800 kg/m3，由于颗粒堆积时存在孔隙，实际样品的密度会小于单个颗粒的密度。所有颗粒的杨氏模量Eeq为5 GPa，泊松比v为1/3，内摩擦角φ为18°，抗张强度t为4.5 MPa,粘聚力c为5 MPa。接触范围系数γint设置为1.01。

表1　颗粒参数设置Table 1 The setting of particles′parameters

Hughes等人曾利用三轴剪切试验导出样品宏观参数，并分析其力学性质是否符合实际情况（Hughes et al.,2014）。本试验借鉴了该方法，利用三轴剪切试验导出宏观参数，并分析其实际意义，过程如下：首先将10 000个颗粒填充于一个尺寸为1:2:1的剪切试验容器中，如图5所示。在Yade软件中，颗粒的绝对尺寸对模拟结果的影响很小（Scholt and Donz,2013），因此可以采用内压缩的方式对样品施压。

随后，让容器壁以足够缓慢的速度压缩样品，保证其始终处于准静止状态。5个试验围压分别为5 MPa，15 MPa，70 MPa，50 MPa，75 MPa，每个围压下的样品都是独立随机生成的。将导出的数据绘制成应力应变曲线图，曲线在弹性变形阶段的斜率即为样品宏观杨氏模量，如图6。

在此基础上，根据莫尔-库伦破裂准则可得到样品的内聚力和内摩擦角，如图7。

样品宏观力学性质：杨氏模量15.34 GPa,内摩擦角28.06°，内聚力0.5 MPa。本实验的参数与其他离散元构造模拟实验所用参数基本一致（Finch et al.,2003; Hardy and Finch,2005; Hughes et al.,2014）。在前人的实验中，用于模拟岩石的样品的杨氏模量比实验室结果大约低一个数量级，这是因为自然界中的岩石体积越大，就可能含有越多的节理和小断层，所以一般情况下岩石体积越大则强度越弱（Bieniawski,1984）。

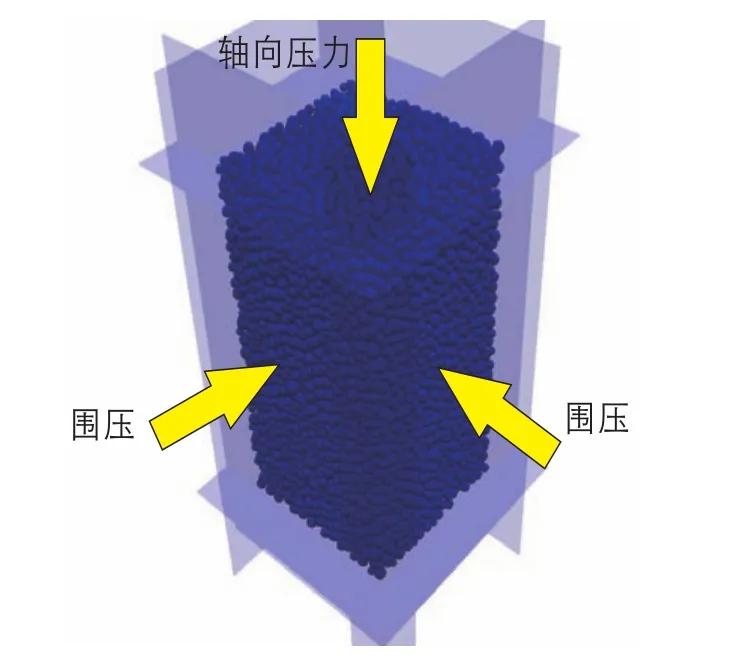
图5　三轴剪切试验模型示例图Fig.5 The example of a trishear model

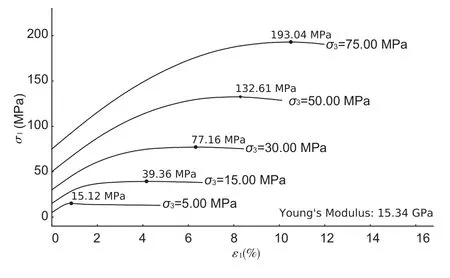
图6　三轴压缩试验下样品的应力应变曲线图（σ1和σ3分别代表轴向应力和围压，ε1代表轴向应变）Fig.6　The stress-strain curve of the sample in trishear tests （The axial stress and confining stress are represented byσ1and σ3respectively.Axial strain is represented by ε1）

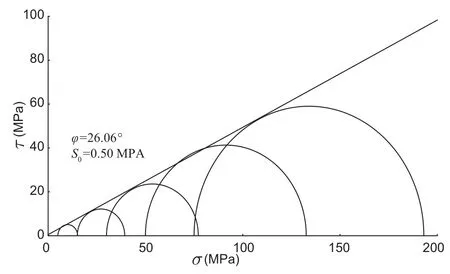
图7　样品莫尔应力圆分析图（φ代表内摩擦角，S0代表内聚力）Fig.7 Mohr’s circle analysis on the sample（Theinternalfriction angle and cohesion are represented by φ and S0respectively）

2.2实验模型及过程

实验模型的边界为一长600 m，高200 m，宽4 m的窄盒，颗粒在空间中随机生成后自由沉降在盒底，沉积结束后仅保留距盒底45 m之内的颗粒。颗粒组成的初始结构长600 m，高45 m，宽4 m，如图8。整个模型的平均密度为2 691 kg/m3。

实验中用不同的颜色区分出6层颗粒，他们的参数相同且各向同性。所有边界都是刚性的，且具有不同的摩擦角，其中侧面边界的摩擦角为18°，底部边界摩擦角为0.5°。左侧活动边界以1 m/s的速度向右端挤压模型，直至缩短量达到30%实验停止。实验中每隔40 000步记录一次变形数据。

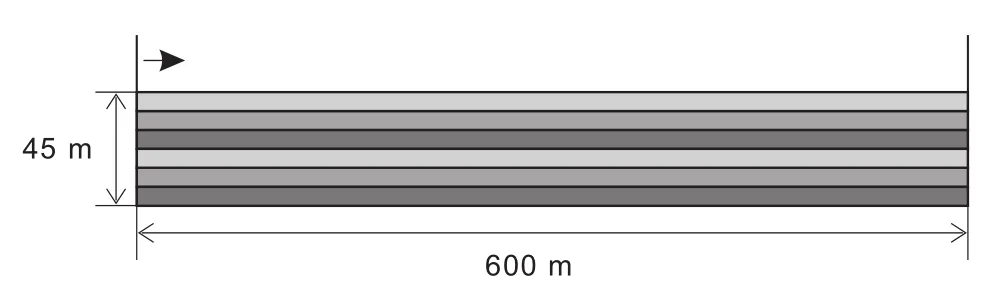
图8　均质模型的初始结构图（各层材料参数均一致；为了方便表示模型形态和内部变形过程，相邻层间填充了不同的颜色，以不同灰度体现）Fig.8　Initial configuration of the homogenous model（All layers consist of particles of the same type.The variation of colors,which is based on the greyscale in this figure,are to reflect the model configuration and the internal deformation processes for convenience）

3　实验结果分析

3.1变形及应变分析

实验各阶段变形情况如图9。

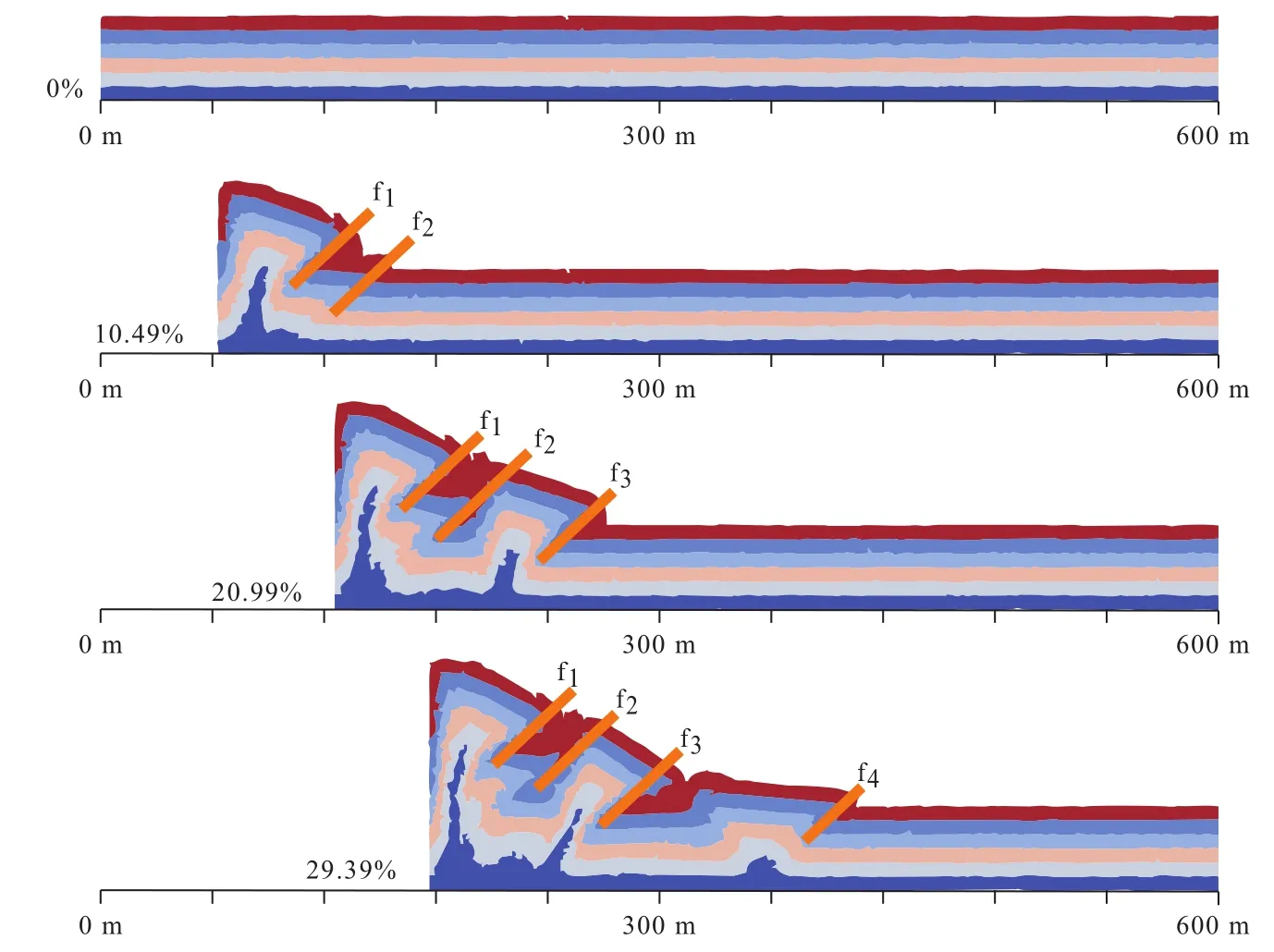
图9　模型变形阶段图（间隔200,000步）（为方便表示变形过程，不同深度的地层着以不同的颜色，但它们的性质相同。断层面的位置和形态由橙线标注，在橙线右上角则对该断层加以注释，方便后文讨论）Fig.9　Evolution of the deformation with an interval of 200,000 steps (Layers at different depth are colored differently,but their properties are the same.The location and geometry of fault planes are marked out with orange lines.The annotations are given on the upper right of each line for the convenience of later discussion)

橙色线条为断面所在位置。在样品缩短量为10.49%时，紧邻挤压端的60 m处一侧出现了两条倾角约30°的逆断层f1与f2，其中靠近挤压端的断层f1规模更大，f2规模较小。在缩短量达到20.99%时，f1与f2活动强度减弱，在距挤压端约110 m处发育第三条主要逆断层f3。在挤压试验接近结束时，距挤压端约120 m处出现第四条的逆断层f4，倾角约40°。该模拟中，断层最先从靠近挤压端的一侧产生，且越靠近推覆前端的断层越新，该现象与孟令森等（2007）得出的结论相符。

模型变形的应变偏量增量如图10。由应变计算原理可知，处于活动中的断面的应变偏量较大，而停止活动的断面上应变偏量为零。模型中最新的断面始终为应变偏量最大之处，且最大应变所在深度较浅，而早先形成的断层的活动较为轻微。该现象表明在变形过程中，如果出现了新的断层则老断层基本停止活动，这与孟令森等（2007）的结论相符合。

变形过程中体应变增量如图11。强烈的体应变集中在活动断面的上盘，且上盘浅部的应变以体膨胀为主。体应变强烈的区域与应变偏量较高的区域相互重叠。

3.2裂缝发育情况

从变形过程中破裂数量统计图（图12）可见4段生成裂缝的高峰期，分别是第0～20 000步，第125 000到160 000步，第235 000到280 000步和第415 000到450 000步。这4个区间依次对应在模型变形过程中先后发育的4个主要断层。

各阶段生成的剪裂缝占总裂缝比率见图13。从图中可知，在裂缝产生的峰值处，剪裂缝生成比率达到最大。整个变形过程中生成裂缝的总量以张裂居多。

图10　应变偏量增量图（间隔200,000步）Fig.10 Strain deviator increments with an interval of 200,000 steps

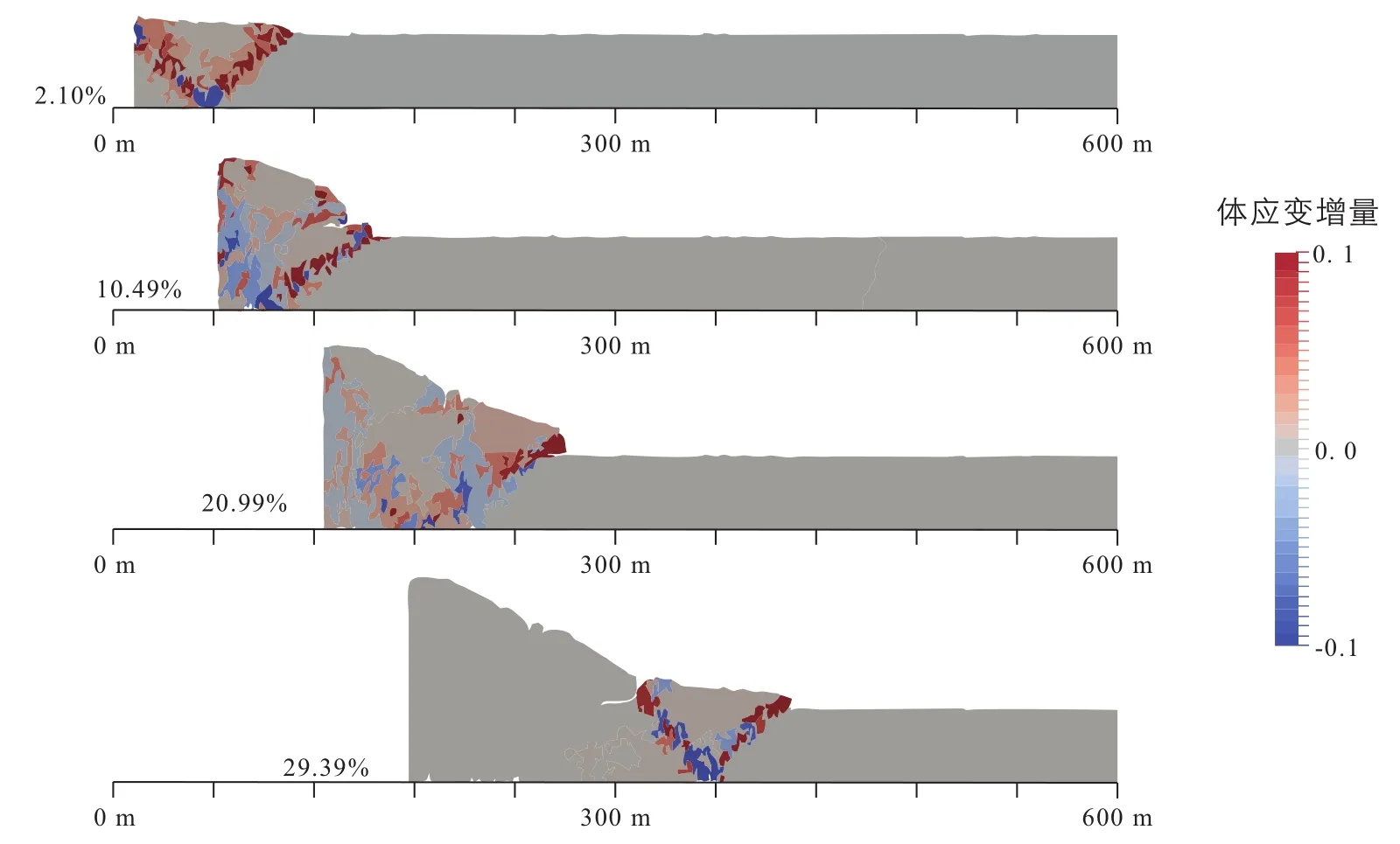
图11　体应变增量图（间隔200,000步）Fig.11 Volumetric strain increments with an interval of 200,000 steps

第一个裂缝峰期内模型的局部变形情况如图14。第一列图片为不同破裂模式分布图，在10 000步时，新生成裂缝数达到最大；靠近挤压端一侧受到边界效应的影响，因此产生了许多新的裂缝，这解释了图12中第一峰期裂缝数量远多于后续峰期中裂缝数量的现象。第二列为固结力分布图，在该组图紧靠挤压端区域中，大量的固结链接发生断裂，其所反映的情况与破裂模式分布图相符。第三列反映了模型中应变偏量的累积变化情况，可见偏应变集中的区域同样是裂缝集中产生的区域，二者所处位置具有明显的对应关系，符合实际情况。第四列为模型体应变变化情况，体应变较强烈的区域同样对应了裂缝集中产生的区域，且应变以体膨胀为主。

在第一个裂缝峰期结束时，该处断层尚未出现明显位移。

图15，16，17分别为第二、三、四个裂缝峰值间距内，模型的局部变形情况、破裂分布和应变分析图。它们反映出如下几个共同点：（1）裂缝生成的峰期在断层产生明显活动之前；（2）裂缝和应变最先集中在断面上，属于同一个断层的裂缝距离断面距离越远则生成时间越晚；（3）裂缝大量发育的区域也是应变强烈的区域，新裂缝数量越多则应变越强烈；（4）同时在每组图中，前一段峰期所对应的断层依旧有明显的位移，但在其断面上生成的裂缝数量远远小于正在发育的新断层。

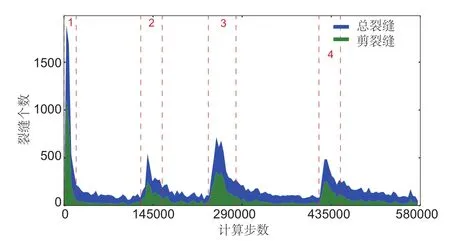
图12　裂缝数量统计Fig.12 Statistics of the number of fractures

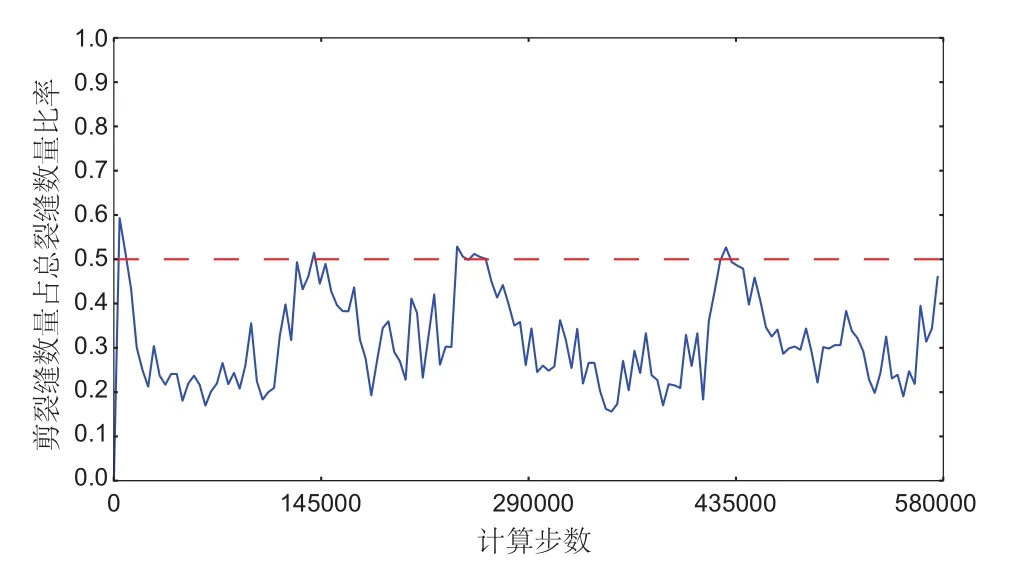
图13　模拟各阶段剪裂缝占总裂缝比率Fig.13 The ratio of shear fractures to total fractures throughout the simulation

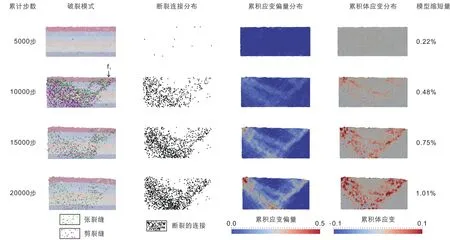
图14　第一裂缝峰期中模型的破裂和应变Fig.14　Fractures and strain distribution in the first peak interval

4　讨论

本实验得出的裂缝密度分布规律与实际情况相符。前人对裂缝密度的研究与测量工作已经较为完善。例如，侯贵廷（1994）详细介绍了裂缝面密度的测量方法，即裂缝密度为裂缝总长度与测量面的面积之比。利用该方法，Ju等（2014）对库车凹陷的一处断层转折褶皱区域进行了裂缝密度测量，发现枢纽处的裂缝密度最大，当测量区域逐渐远离断层时，测得的裂缝密度逐渐下降（图18）。张庆莲等（2010）对新疆巴楚地区走滑断裂的裂缝密度进行了测量，同样揭示了越靠近断层则裂缝密度越大的规律。Gundmundsson等（2010）采用单位距离内的裂缝个数来表示裂缝密度。他们利用该方法在西挪威的一个断层周边统计了裂缝密度的分布情况，发现在一定距离内离断层越远的区域裂缝密度越低。Johri等（2014）对美国加利福尼亚州近圣安地列斯断层的SSC储层的钻井数据进行了研究，同样发现了断层附近区域的裂缝密度偏高。

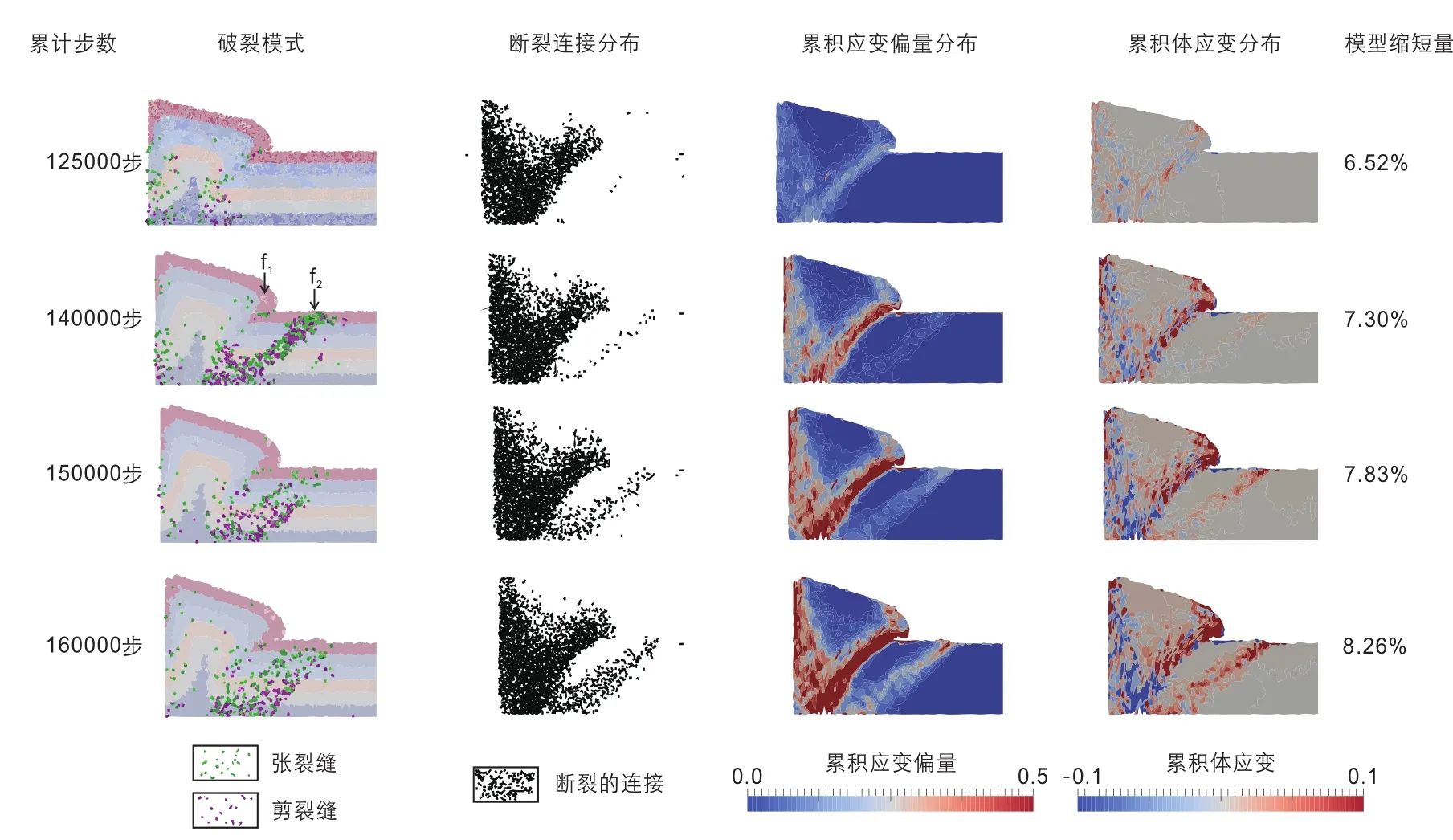
图15　第二裂缝峰期中模型的破裂和应变Fig.15　Fractures and strain distribution in the second peak interval

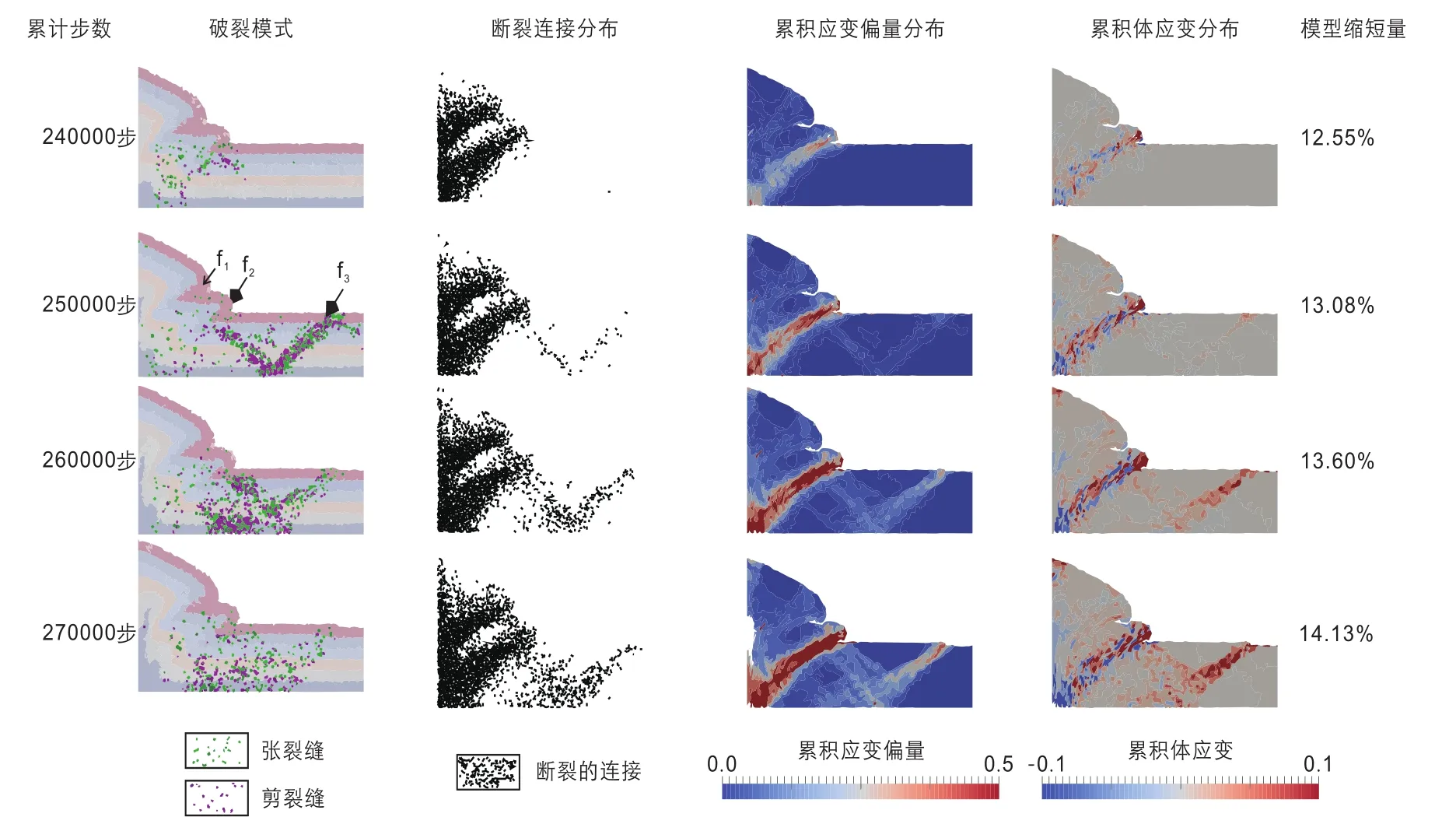
图16　第三裂缝峰期中模型的破裂和应变Fig.16 Fractures and strain distribution in the third peak interval

本实验中得到的应变规律亦与实际情况相符合。此前Johri等（2014）在对SSC储层的钻井资料研究中指出断层核心区域的应变较大；Smart等（2012）对断层相关褶皱进行了有限元模拟和应力应变分析，其结果同样表明应变主要集中在枢纽区域。

但是，本实验也存在不足之处。由于各个裂缝数据都以离散点的形式记录，而在紧邻断层面的空间中的裂缝数据点非常多，因此模型中主要断层面的位置难以精确界定；此外，该裂缝数据记录方式也导致各裂缝的宽度、延伸方向和延伸长度都无法得知。在这种情况下，侯贵廷等人所用的裂缝密度测量公式就不再适用于本实验了。如何将离散元模型的裂缝密度数据与实际情况做定量对比，是今后需要解决的问题。

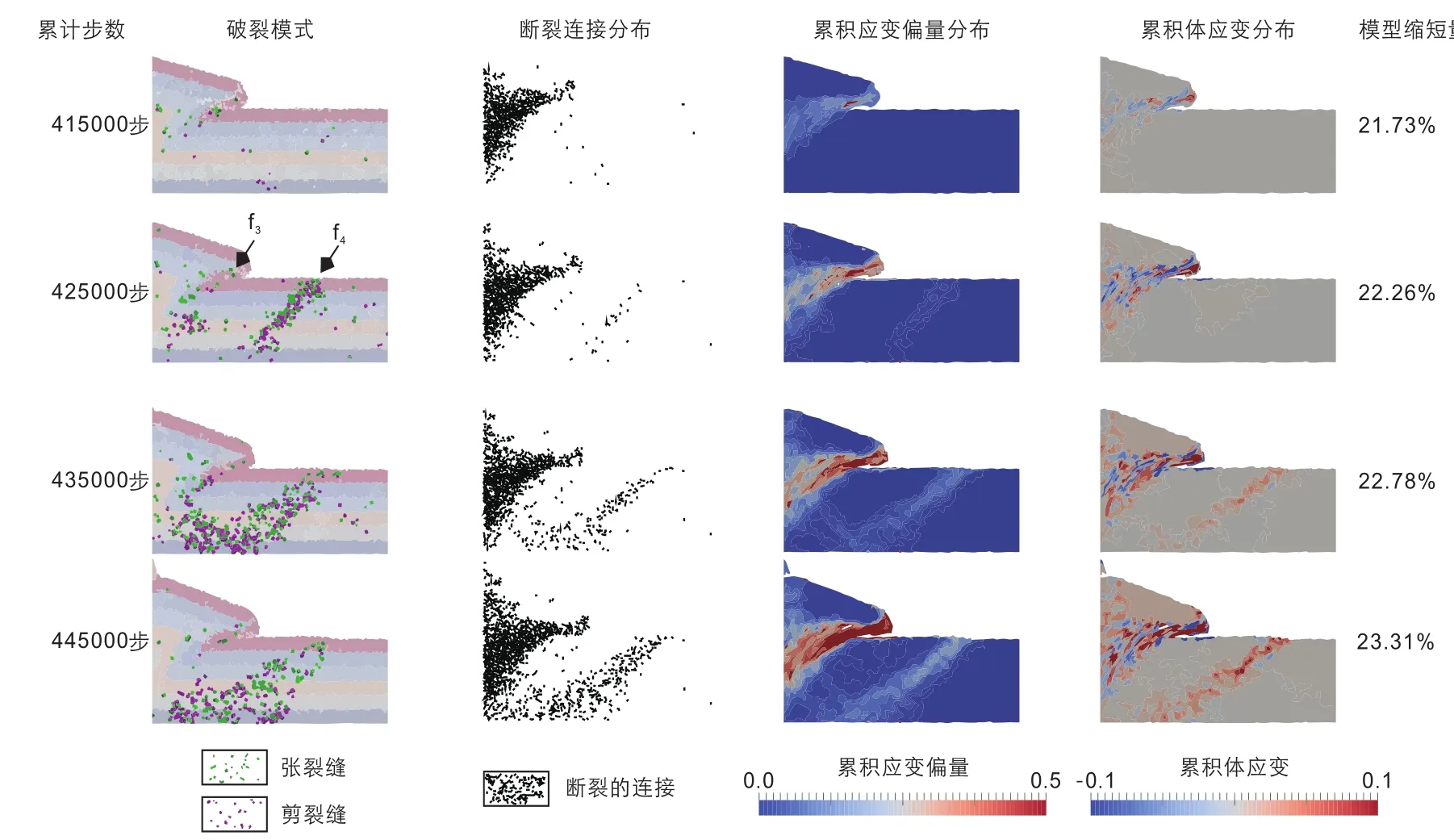
图17　第四裂缝峰期中模型的破裂和应变Fig.17 Fractures and strain distribution in the fourth peak interval

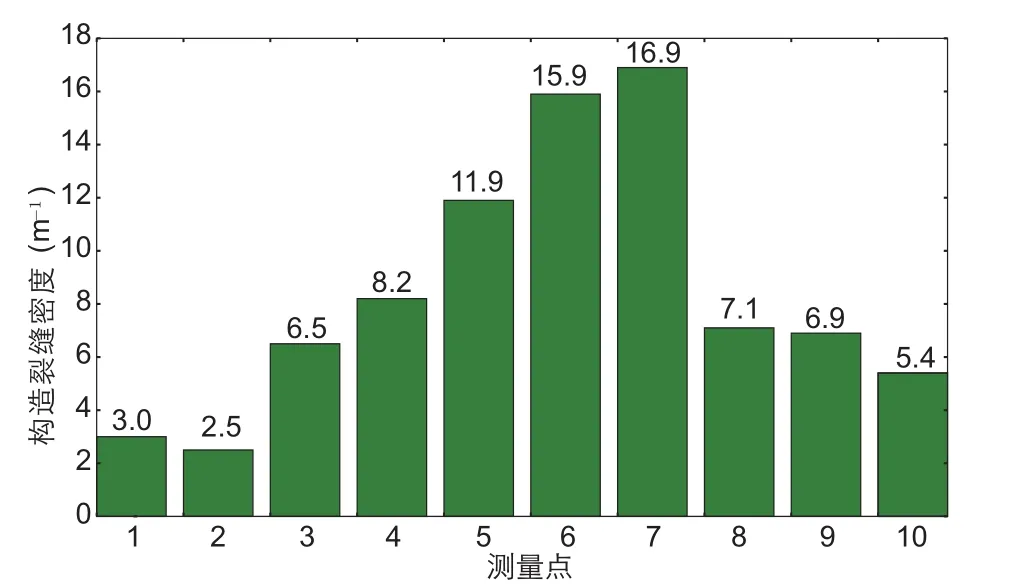
图18　库车凹陷一断层转折褶皱裂缝密度统计图（最靠近断层区域的7号点对应着最高的裂缝密度，而测量开始的1号点与10号点上断层密度最小；Ju et al.,2014）Fig.18 Statistics of fracture densities at different measuring points on a fault-bend fold at Kuqa Depression （Point 7,the one closet to the fault plane,has the highest density of all; While point 1 and 10,the starting and ending measuring points which are far from the fault,bear much lower fracture density）

5　结论

本实验利用离散元方法模拟了挤压环境下滑脱构造的变形过程，并进行了裂缝分析和应变分析，得到了如下结论：

（1）在挤压环境的滑脱构造中，裂缝产生的高峰期先于断层明显活动期，局部区域内聚集的大量断裂是产生断层的诱因之一。已经出现明显活动的断层中产生的裂缝较少；

（2）裂缝集中区域和应变集中区域相互重叠，裂缝越发育则应变越强烈；

（3）受同一断层影响的裂缝首先在断面上集中出现，随后在断面周边区域产生。在断层影响范围内，裂缝距离断面越远则形成时间越晚；

本实验表明，离散元方法很好地模拟了岩体受挤压产生形变的过程，并能够详细反映模型内部的应变和裂缝分布情况。该结果也同时揭示了离散元方法在今后裂缝预测研究中的巨大潜力。

参考文献（References）:

陈波，田崇鲁.1998.储层构造裂缝数值模拟技术的应用实例[J].石油学报，19(4): 50-54.

单家增，张占文，陈绍生，等.2005.大民屯凹陷安福屯潜山带古构造应力场与裂缝发育特征的光弹物理模拟实验研究[J].石油勘探与开发，31(4): 15-18.

何雨丹，魏春光.2007.裂缝型油气藏勘探评价面临的挑战及发展方向[J].地球物理学进展，22(2): 537-543.

侯贵廷.1994.裂缝的分形分析方法[J].应用基础与工程科学学报，2(4): 301-306.

刘泉声，吴月秀，刘滨.2011.应力对裂隙岩体等效渗透系数影响的离散元分析[J].岩石力学与工程学报，30(1): 176-183.

龙鹏宇，张金川，唐玄，等.2011.泥页岩裂缝发育特征及其对页岩气勘探和开发的影响[J].天然气地球科学，22(3): 525-532.

马寅生，张兴，Others.2002.黄骅坳陷新生代构造应力场演化的光弹模拟与石油地质条件分析[J].地质力学学报，8(3): 219-228.

孟令森，尹宏伟，张洁，等.2007.岩石强度和应变速率对水平挤压变形影响的离散元模拟[J].岩石学报，23(11): 2918-2926.

聂海宽，唐玄，边瑞康.2009.页岩气成藏控制因素及中国南方页岩气发育有利区预测[J].石油学报，30(4): 484-491.

司马军，蒋明镜，周创兵.2013.黏性土干缩开裂过程离散元数值模拟[J].岩土工程学报，35(zk2): 286-291.

孙萍，彭建兵，范文.2008.地裂缝错动对地铁区间隧道影响的三维离散元分析[J].工程地质学报，5: 710-714.

文世鹏，李德同.1996.储层构造裂缝数值模拟技术[J].石油大学学报:自然科学版，20(5): 17-24.

徐文杰，张海洋，于玉贞.2012.基于离散元的土石混合体大型直剪数值试验研究[J].颗粒材料计算力学研究进展.

杨艳，常晓林，周伟，等.2012.裂隙岩体水力劈裂的颗粒离散元数值模拟[J].四川大学学报（自然科学版），44(5): 78-85.

张洁，尹宏伟，孟令森，等.2008a.主动底辟盐构造的二维离散元模拟[J].地球物理学进展，23(6): 1924-1930.

张洁，尹宏伟，徐士进.2008b.用离散元方法讨论岩石强度对主动底辟盐构造断层分布模式的影响[J].南京大学学报:自然科学版，44(6): 642-652.

张庆莲，侯贵廷，潘文庆，等.2010.新疆巴楚地区走滑断裂对碳酸盐岩构造裂缝发育的控制[J].地质通报，29(8): 1160-1167.

Abdelmalak M M,Mourgues R,Galland O,et al.2012.Fracture mode analysis and related surface deformation during dyke intrusion: Results from 2D experimental modelling [J].Earth Planet.Sc.Lett.,359: 93-105.

Bieniawski Z L A T.1984.Rock mechanics design in mining and tunnelling [M] A.A.Balkema,1-272.

Catalano E,Chareyre B and Barth E Lemy E.2014.Pore-scale modeling of fluid-particles interaction and emerging poromechanical effects [J].Int.J.Numer.Anal.Met.,38(1): 51-71.

Cundall P A and Strack O D.1979.A discrete numerical model for granular assemblies [J].Geotechnique,29(1): 47-65.

Donze F V,Bouchez J,Magnier S A.1997.Modeling fractures in rock blasting [J].Int.J.Rock Mech.Min.,34(8): 1153-1163.

Finch E,Hardy S and Gawthorpe R.2003.Discrete element modelling of contractional fault-propagation folding above rigid basement fault blocks [J].J Struct.Geol.,25(4): 515-528.

Gale J F,Reed R M and Holder J.2007.Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments [J].AAPG Bull.,91(4): 603-622.

Gudmundsson A,Simmenes T H,Larsen B,et al.2010.Effects of internal structure and local stresses on fracture propagation,deflection,and arrest in fault zones [J].J.Struct.Geol.,32(11): 1643-1655.

Hardy S and Finch E.2005.Discrete-element modelling of detachment folding [J].Basin Res.,17(4): 507-520.

Hart R,Cundall P A and Lemos J.1988.Formulation of a three-dimensional distinct element model-Part II.Mechanical calculations for motion and interaction of a system composed of many polyhedral blocks [Z].Elsevier: 117-125.

Hughes A N,Benesh N P and Shaw J H.2014.Factors that control the development of fault-bend versus fault-propagation folds: Insights from mechanical models based on the discrete element method (DEM) [J].J.Struct.Geol.,68: 121-141.

Inc I C G.2012.PFC2D/3D (Particle Flow Code In 2/3 Dimensions),Version 4.0 [G].Minneapolis.

Iwashita K and Oda M.2000.Micro-deformation mechanism of shear banding process based on modified distinct element method [J].Powder Technol.,109(1): 192-205.

Johri M,Zoback M D and Hennings P.2014.A scaling law to characterize fault-damage zones at reservoir depths [J].AAPG Bull.,98(10): 2057-2079.

Ju W,Hou G and Zhang B.2014.Insights into the damage zones in fault-bend folds from geomechanical models and field data [J].Tectonophysics,610: 182-194.

Kozicki J and Donz E F V.2009.Yade-open dem: an open-source software using a discrete element method to simulate granular material [J].Eng.Computation,26(7): 786-805.

Kozicki J and Donz E F V.2008.A new open-source software developed for numerical simulations using discrete modeling methods [J].Comput.Method Appl.M.,197(49): 4429-4443.

Lee S and Dan N T.2005.Probabilistic landslide susceptibility mapping in the Lai Chau province of Vietnam: focus on the relationship between tectonic fractures and landslides [J].Environmental Geology,48(6): 778-787.

Morgan J K.1997.Studying Submarine Accretionary Prisms in a'Numerical Sandbox': Simulations using the Distinct Element Method [Z].707.

Potyondy D O and Cundall P A.2004.A bonded-particle model for rock [J].Int.J.Rock Mech.Min.,41(8): 1329-1364.

Saltzer S D and Pollard D D.1992.Distinct element modeling of structures formed in sedimentary overburden by extensional reactivation of basement normal faults [J].Tectonics,11(1): 165-174.

Scholt E S L and Donz E F E D E.2013.A DEM model for soft and hard rocks: Role of grain interlocking on strength [J].J.Mech.Phys.Solids.,61(2): 352-369.

Scholt E S L and Donz E F E D E.2013.A DEM model for soft and hard rocks: Role of grain interlocking on strength [J].J.Mech.Phys.Solids.,61(2): 352-369.

Shiu W,Donze F and Daudeville L.2008.Compaction process in concrete during missile impact: a DEM analysis [J].Comput.Concrete.,5(4): 329-342.

Smilauer V V S,Catalano E,Chareyre B,et al.2014.Yade Documentation [M].The Yade Project,129-133.

Smart K J,Ferrill D A,Morris A P,et al.2012.Geomechanical modeling of stress and strain evolution during contractional fault-related folding [J].Tectonophysics,576: 171-196.

Strayer L M,Erickson S G and Suppe J.2004.Influence of growth strata on the evolution of fault-related folds-distinct-element models [J].AAPG Memoir,82: 413-437

Strayer L M and Suppe J.2002.Out-of-plane motion of a thrust sheet during along-strike propagation of a thrust ramp: a distinct-element approach [J].J Struct.Geol.,24(4): 637-650.

Yin X and Zhang Q.2007.Evolution of the Structural Stress and Its Function During Oil/Gas Accumulation in Bohai Sea [J].Marine Geology and Quaternary Geology,27(5): 45.

Technologyof Strain Analysisand Fracture Prediction Basedon DEMNumerical Simulation

CAI Shenyang1,YIN Hongwei1*,Li Changsheng1,JIA Dong1,WANG Wei1CHEN Zhuxin2,WEI Dongtao3
1.Insititute of Energy Sciences,School of Earth Sciences and Engineering,Nanjing University,Nanjing 210023,China; 2.Research Institute of Petroleum Exploration & Development,Beijing 100083,China; 3.PetroChina Exploration Development Research Institute (Northwest),Lanzhou 730022,China

Abstract:The application of strain analysis and fracture prediction technology is of great importance in geosciences.However,the discrete element method (DEM),which is suitable for solving problems with discontinuous property,has not been widely used in this field.This paper presents an attempt to construct DEM model of a bulk of rock with realistic properties,followed by a simulation of the evolution of a compressional detachment structure.The strain distribution and fracture formation are analyzed afterwards.As to the detachment structure,the result shows that the interval in which the fracture generation reaches its peak precedes the one in which the fault appears the most active.Additionally,fractures and strain distribution share the same concentrating areas,and the number of fractures is proportional to the intensity of the strain.Also,fractures that are related to the same fault first concentrate on its fault plane,then appear in the vicinity of that plane.It indicates that,within the range of fault influence,the further a fracture is from the fault plane,the later it is generated.Above all,the result has revealed a great application potential of DEM in the field of strain analysis and fracture prediction.

Key words:discrete element method; strain analysis; fracture prediction

Corresponding author:YIN Hongwei,Professor; E-mail: hwyin@nju.edu.cn

*通讯作者：尹宏伟，男，1971年生，教授，博士，主要从事含油气盆地构造与沉积特征的研究与教学工作; E-mail: hwyin@nju.edu.cn

作者简介：蔡申阳，男，1992年生，实验助理; E-mail: sycai@outlook.com

基金项目：江苏省科技支撑计划项目（BE2013115）；国家重点基础研究发展计划（“973”：2012CB214703）；国家自然科学基金项目（41272227；41572187）联合资助

收稿日期：2015-11-30；修回日期：2016-01-18

DOI:10.16108/j.issn1006-7493.2015235

中图分类号：P618.13

文献标识码：A

文章编号：1006-7493（2016）01-0183-11