基于离散元法的水力压裂数值模拟
顾颖凡,卢毅,刘兵,刘春,3,*.南京大学地球科学与工程学院,南京003 .国土资源部地裂缝地质灾害重点实验室,江苏省地质调查研究院,南京0049 3.南京大学(苏州)高新技术研究院,苏州53
基于离散元法的水力压裂数值模拟
顾颖凡1,卢毅2,刘兵1,刘春1,3,*
1.南京大学地球科学与工程学院,南京210023 2.国土资源部地裂缝地质灾害重点实验室,江苏省地质调查研究院,南京210049 3.南京大学(苏州)高新技术研究院,苏州215123
摘要:不同条件下水压裂隙的发展特性对有效开采页岩气具有重要的指导作用。针对岩体在微观上为颗粒和孔隙的结构系统,提出离散元水力压裂数值模拟方法,离散元能量转化和能量守恒计算方法,建立了相应的三维离散元模型。采用自主研发的三维离散元模拟软件MatDEM(3D),通过控制模型的竖向应变与颗粒直径,来模拟地层中的应力与压裂速率的变化。模拟结果表明:(1)水力压裂产生裂隙的数量和方向受岩石的各向异性,压力状态和变化速率所影响。(2)裂隙在压缩波传播时发展,当水压力高速增加时,诱发的裂隙数量增多,并且有效能量(断裂热)百分比也随之增加,压裂作用也变得更明显。(3)当竖向应变为零时,50%的裂隙呈垂直状态,当竖向应变为-1×10(-4)时,裂隙趋于沿着最大压力方向发展,竖向裂隙的百分率增大。数值模拟和能量分析为定量地研究岩石水力压裂过程提供了一个新的方法。
关键词:水力压裂;离散元;MatDEM;能量
1 引言
页岩气主要成分是甲烷,是一种高效、清洁、低碳的理想替代能源。合理利用页岩气资源可以有效的减轻中国目前的环境问题,提高能源开发利用整体效益。水力压裂技术是页岩气开发的核心技术之一(唐颖等,2011)。早在1947年,美国Stanolind油气公司首次将水力压裂技术投入使用,随后水力压裂技术便受到广泛关注并迅速发展(张搏等,2015)。由于中国页岩气储层的地质构造较为复杂,大规模的工业化开采亟需有关技术的研究与发展(孙可明等,2014)。科学全面地了解不同的岩石性质和应力条件下,水力压裂作用机制与压裂纹发展特性至关重要。
数值模拟方法被认为是认识裂缝扩展规律经济而有效的方法,已成为一种研究水力压裂技术的有效途径。目前,一些研究学者通过运用计算机数值模拟软件来模拟压裂过程,取得了较好的成果(连志龙等,2009;彪仿俊等,2011;彭成勇等,2014)。连志龙等(2009)运用有限元数值模拟软件ABAQUS,模拟了地层中各种复杂因素对裂缝扩展的影响,分析得到了起裂压力、裂缝扩展长度和最大缝宽与地层中各参数的关系。彪仿俊等(2011)建立了一套三维有限元模型,对水力压裂中水平裂缝的起裂和扩展过程进行了数值模拟,研究各种参数对水平缝扩展的影响。彭成勇等(2014)建立了斜井中三维裂缝发展形态的有限元模型,综合考虑了岩层渗透性和孔隙度对裂缝发展的影响,研究斜井微环隙在水力压裂过程中的扩展特性。
目前,水力压裂模拟大多采用基于有限元等的连续介质方法,而储层岩石是由颗粒和孔隙构成的不连续介质,基于连续介质方法较难以真实地反映微观结构的对裂隙发展的作用。离散元法(Cundall and Strack,1979)是解决不连续物质问题一种重要方法。在离散元法中,模型由一系列颗粒堆积构成,这些颗粒通过不同的组合来表示连续的或者非连续的物质。离散元法能模拟地质体的大变形、断裂和破碎的动态演变过程(Hazzard et al.,2000)。此种方法已经被运用在模拟和解释各种地质现象,包括地质体的破坏问题和地质体的不连续性问题上,例如水力压裂的研究(Shimizu et al.,2011; Eshiet et al.,2013)。
本文建立了紧密堆积的三维离散元模型,通过转化公式来确定模型中颗粒力学参数,构建起具有特定弹性和破坏性质的离散元模型,并研究了离散元模型中的能量转化和能量守恒。在此基础上,模拟了不同竖向应变与加压速率下裂隙发展特性,尝试在水力压裂裂缝发展机制和裂缝发展模式预测方面上提供新的思路。本文为定量地研究页岩气水力压裂过程提供了一个新的方法,并有待于进一步的实践与验证。
2 三维紧密堆积离散元模型
研究采用三维紧密堆积离散元模型(图1a),其由一系列相同尺寸和力学性质的颗粒堆积构成。颗粒间通过法向弹簧力(Fn)相互作用(Hardy and Finch,2006; Yin et al.,2009):
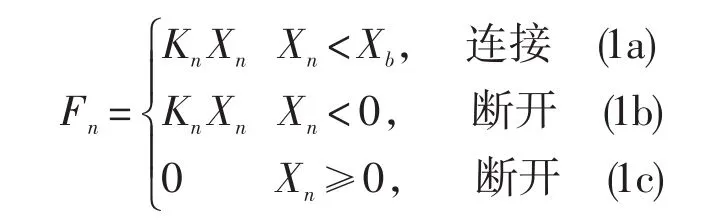
其中Kn是法向刚度;Xn是法向相对位移(图1b);Xb是断裂位移。颗粒最初是相互连接,并受拉力或压力的作用(式1a)。当两个颗粒之间的法向相对位移Xn超过断裂位移Xb,连接断裂,颗粒的拉力消失。此时,Xn大于等于零时,两个颗粒之间Fn为零(式1c),连接断裂。但是,当这两个颗粒回复到压缩状态,颗粒间斥力仍然存在(式1b)。
图1c表示两个颗粒在切向方向上通过一个可断裂的弹簧连接,并模拟剪切变形和剪切力。剪切力(FS)由下式决定(Cundall and Strack,1979; Hardy et al,2009):

其中KS是剪切刚度,XS是颗粒间切向相对位移。在数值模拟中,剪切力通过每个时间步的计算累积得到(Cundall and Strack,1979)。对于一个完整的连接来说,最大的剪切力(FSmax)由库伦摩擦力来确定:
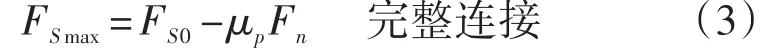
其中Fs0是颗粒之间的剪切阻力;μp是颗粒之间的摩擦系数;Fn是法向力(压缩为负)。
当外力超过式(3)中的FSmax时,两个颗粒之间的连接会断开。剪切力(FS)的大小被限制为小于或等于在下式中的最大剪切值(FSmax'):

当颗粒间连接断裂,且颗粒间剪切力超过最大剪切力FSmax',颗粒会发生相对位移,它们之间的滑动摩擦力即为FSmax'。
3 模型中能量转换与能量守恒
岩体水力压裂过程伴随着弹性能、动能、断裂能和热能等能量的产生和转化。定量地研究这些能量的变化,有利于认识水力压裂机制和规律。离散元模型中的机械能包括动能,弹性势能和重力势能(Mora and Place,1998; Place and Mora,1999)。在数值模拟中,机械能通过三种方式转化为热能:黏滞力的作用、颗粒间连接断裂作用与摩擦作用。这三种作用分别产生粘滞热,断裂热和摩擦热。离散元法中,使用时间步算法来进行计算模拟(Cundall and Strack,1979; Potyondy and Cundall,2004),而热量在每个时间步中计算累积。
3.1粘滞热
岩体中的应力波(地震波)由于摩擦等因素作用而衰减,机械能逐步转化成热能(Hazzard et al.,2000)。在离散元模型中,采用粘滞阻尼来减弱模型中的震动波,避免系统动能不断增强(Mora and Place,1993,1994; Place et al.,2002; Finch et al.,2003)。粘滞力(Fv)定义为:

其中η是粘滞系数,v是颗粒速度。由于模拟中的时间步非常小,认为在一个时间步中颗粒的速度为常数。粘滞热(Qv)在粘滞力作用下生成,由以下方程来计算:

其中dx为在当前时间步中颗粒的位移。
3.2断裂热
当一个完整的连接断裂时,颗粒之间法向弹力和切向弹力产生的弹性势能将会转为热能而消散。在连接断开的过程中,产生的热量等于减少的弹性势能。如果颗粒之间的法向力为拉力,那么当颗粒之间相互的连接断开的时候法向与切向的弹性势能Ee减少到0。断裂热(Qb)为法向和切向弹簧的弹性势能的总和:
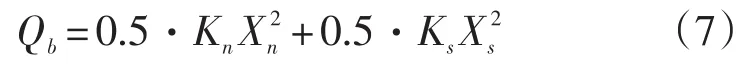
当两连接颗粒处于相互挤压状态,颗粒间剪切力达到FSmax时(式3),颗粒连接断裂并相对滑动,粒间剪切力减小到FSmax'(式4)。此时,断裂热等于颗粒间切向弹簧热能的减少量,并可由下式计算得到:
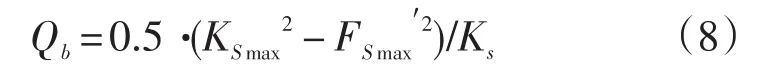
其中KS是颗粒之间的剪切刚度。
3.3摩擦热
颗粒相互滑动时产生摩擦热(Qf),其定义为平均滑动摩擦力和滑动距离(dS)的乘积:
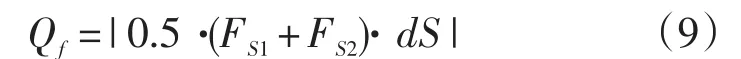
其中Fs1和Fs2分别为当前时间步开始时和结束时的滑动摩擦力(即式4中的FSmax');dS为滑动距离。由于颗粒之间的法向力在每一个时间点都不同,按照式4中得出Fs1和Fs2是不同的,所以在方程中使用平均摩擦力来计算。
4 水力压裂离散元数值模拟
4.1建模与数值模拟
基于上文所述原理,我们自主研发了大型三维离散元模拟软件MatDEM3D(Liu et al.,2013)。在本研究中,采用此软件建立三维球体孔隙模型,并模拟岩石中的水力压裂过程。如图2a所示,立方体模型的边长(L)为0.06 m,它由一系列直径为0.001 m的颗粒紧密堆积连接组成。这种紧密堆积的离散元模型具有特定力学性质,并可以通过转换公式确定颗粒间的5个力学参数(Liu et al.,2013)。附录A给出三维紧密堆积模型的颗粒间力学参数与模型力学性质之间的转换公式。表1给出转换公式中输入的岩石力学参数,计算得到的颗粒间的力学参数,以及实测的岩石模型力学参数。
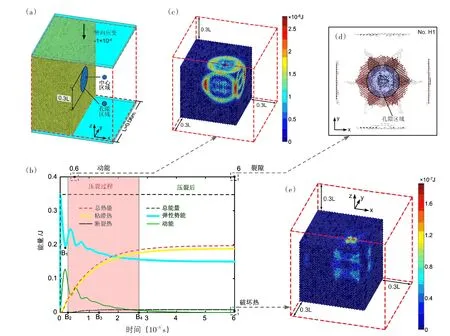
图2 (a)离散元模型的中心被水颗粒填充;(b)模拟过程中能量变化曲线;(c)在0.6×10-5s时的动能分布;(d)在0.6×10-5s(εzz为-1×10-4)时裂隙分布顶视图;(e)断裂热Fig.2 (a) The center of the discrete element model is filled of water particles; (b) Energy conversion curves during simulation; (c) Kinetic energy of model at time 0.6×10-5s; (d) Top view of the fractures 6×10-5s (εzzis -1×10-4); (e) breaking

表1 水力压裂模型中力学参数与颗粒间参数(颗粒直径为0.001 m)Table 1 Mechanical propertiesand inter-particle parameters of hydraulic fracturing model (particle diameter is 0.001 m)
为模拟水压力作用,在模型的中心划出球形孔区域,直径为0.018 m(0.3·L)。孔中充满了断开连接的松散“水颗粒”,即颗粒之间的摩擦力和剪切刚度全为零(μp=0且Ks=0)。由于水没有抗拉强度与抗压强度,断裂位移和抗剪力都为零(Xb= 0且Fs0=0)。水颗粒的法向刚度可以由水的体积弹性模量(K)来估计,体积弹性模量(K)为2.2 GPa。由于水颗粒剪切刚度需为零,当水颗粒模型的泊松比(v)设为0.2时,由附录A计算出的切向刚度为0,符合设定的要求。据公式E=3K·(1-2v),来计算水颗粒集合的等价杨氏模量(E)。将E与v代入附录A中公式来计算法向刚度。转换公式是针对完整连接的,而数值模拟中,水颗粒的初始连接全设为断裂,实际泊松比为0.5。基于以上推导,得到水颗粒间的参数如表1所示。
模拟中,水压的影响通过水颗粒之间的相互运动和相互作用来实现,因此需要大量的颗粒。MatDEM3D采用了创新的技术,可实现大规模离散元模拟。此模型由297 578个颗粒组成,其中4 056个颗粒在孔隙区域,512个颗粒在区域中心(图2a中直径为0.009 m的球形区域)。原始模型中的邻近接触颗粒相互连接。模型的顶端和底部由光滑的平面组成,侧面四个边界是无侧限的。模型被两个平面压缩,直到竖向应变(εzz)为-1×10-4。模拟开始时,核心颗粒直径增加1%,核心区域“水压”增至27 MPa。由于较大的瞬时水压作用,模型中产生相应的压缩波(图2c),颗粒间连接在压缩波传播时断裂。
图2b为压缩波形成和传播过程中能量转换曲线。水压力在0点产生,弹性势能(Ee)值跳跃到0.35 J,随后迅速转化为动能(Ek)。时间点B1,压缩波到达孔隙边界,随后发展到孔隙外部(图2c)。由于水压力作用,孔隙区域在时间点B2扩大且开始破裂。在时间点B3时,压缩波到达模型的边界,之后断裂热保持不变。图2d所示孔隙区域破坏特征。图2e显示了模型中的断裂热。由于模型侧面是无约束的,当压力波到达的时候,裂隙趋于沿着边界表面发展。
4.2不同竖向应变与压裂速率
为研究不同的竖向应变与压裂速率对裂隙数量与分布的影响,模拟了不同参数下的破裂过程。如图2a为竖向应变为零时模型H0的顶视图,其破裂模式与图2d非常的相似。在低压裂速率下,经过50个时间步,中心颗粒的直径增加了1%。图3b-c分别为低压裂速率竖向应变-1×10-4和0时的破裂结果。当压裂速率很低时,所产生的压缩波比高速率下弱的多。所以,在图3b-c中裂隙数量明显低于在图2d和3a中的数量。
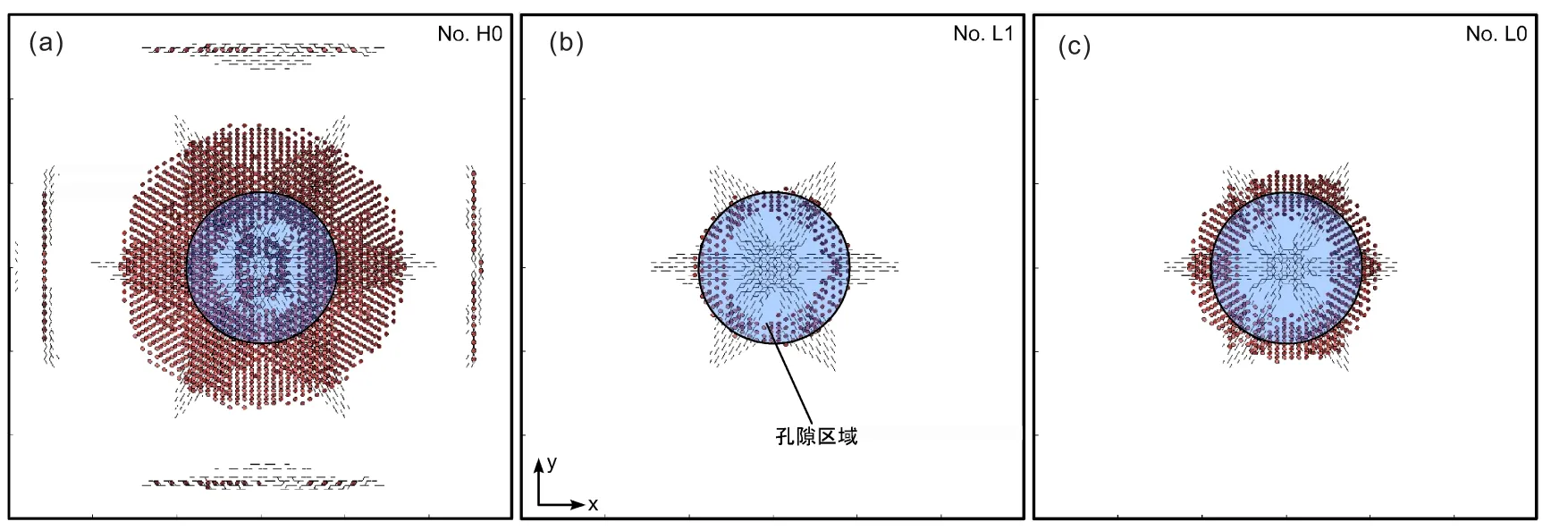
图3 不同条件下的裂隙分布顶视图,暗色的部分为竖向发展裂隙。Fig.3 Top views of fractures under different conditions.Note that dark segments are vertical fractures.

表2 在不同竖向应变与压裂速率下的裂隙数量与能量Table 2 Fracture numbers and energy of simulations with different vertical strains and hydraulic speeds
表2给出了数值模拟得到的裂隙数量和能量值。表格中裂隙数是根据颗粒间连接的断开情况判断的,模型中两个颗粒间连接断开即视作产生一个裂隙。可以看出,模型H1、H0产生的裂隙数量是L1、L0的5.9倍。表2给出有效能百分比,其定义为断裂热与输入弹性势能的比值。由表得,H1、H0的平均有效能百分率为2.71%,大约为L1、L0的三倍。因此,当压裂速率较高时,裂隙发育数量增多,且能量输入更为有效。表2说明当竖向应变为零时,50%的裂隙呈垂直状态,由于没有竖向压应变时,颗粒相对松散,产生裂隙数量较多,无侧限时,水平方向应变大,容易产生竖向的裂隙。当竖向应变为-1×10-4时,裂隙趋于平行最大压应力方向发展,竖向裂隙的百分率较大。
5 结论
针对岩体在微观上为颗粒和孔隙的结构系统的特点,本文采用自主研发的三维离散元模拟软件MatDEM3D完成一系列数值模拟。模拟过程中,随着边界位移的逐渐增加,模型中的总能量增量也逐步的增加,且总是与外力做的功相等。当模型破裂,储存的应力能被释放后转换成动能与热能。但是,机械能与热能的总量总为常数。模拟结果显示,模型是一个孤立的体系,遵循能量守恒规律。
在本研究中,通过水颗粒之间相对运动和相互作用来产生水压力和压裂作用。模拟结果显示,水力压裂裂隙的数量和方向受岩石的各向异性,水压力大小和水压力增加速率影响等因素影响。当压裂速率很高时,裂隙数量增多,并且有效能百分比也随之增加,压裂的作用更明显。本文的初步研究表明,基于MatDEM3D的离散元水力压裂模型能有效实现压裂过程动态模拟和能量分析,为页岩气水力压裂数值模拟研究提供了一个新的途径。相关理论和模型还有待于深入研究,以及进一步实践的检验。
附录A:岩石力学性质与颗粒间力学参数的转换公式。颗粒间的法向刚度(Kn),切向刚度(Ks),断裂位移(Xb),初始剪切抗剪力(Fs0),摩擦系数(μp)可以通过杨氏模量(E),泊松比(v),抗拉强度(Tu),抗压强度(Cu)和内摩擦系数(μi)得到:
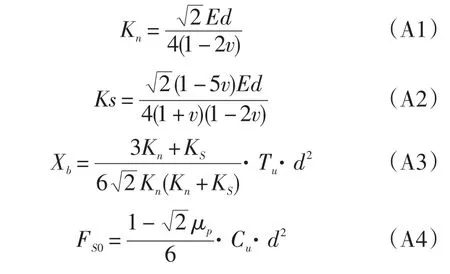
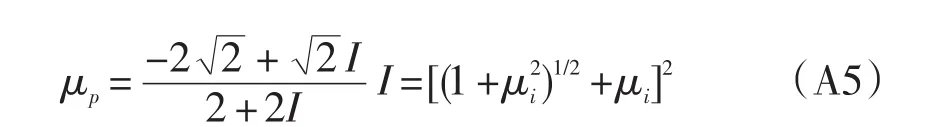
参考文献(References):
彪仿俊,刘合,张士诚,等.2011.水力压裂水平裂缝影响参数的数值模拟研究[J].工程力学,28(10): 228-235.
连志龙,张劲,王秀喜,等.2009.水力压裂扩展特性的数值模拟研究[J].岩土力学,30(1): 169-174.
彭成勇,朱海燕,刘书杰,等.2014.斜井水力压裂三维裂缝动态扩展数值模拟[J].科技导报,32(2): 37-43.
唐颖,唐玄,王广源,等.2011.页岩气开发水力压裂技术综述[J].地质通报,30(2/3): 393-399.
孙可明,王松,张树翠.2014.页岩气储层水力压裂裂纹扩展数值模拟[J].辽宁工程技术大学学报(自然科学版),33(1): 5-10.
张搏,李晓,王宇,等.2015.油气藏水力压裂计算模拟技术研究现状与展望[J].工程地质学报,23(2): 301-310.
Cundall P and Strack O.1979.A discrete element model for granular assemblies [J] Geotechnique,29(1): 47-65.
Eshiet K,Sheng Y,and Ye J.2013.Microscopic modelling of the hydraulic fracturing process [J].Environmental Earth Sciences,68(4):1169-1186.
Finch E,Hardy S and Gawthorpe R.2003.Discrete element modelling of contractional fault-propagation folding above rigid basement fault blocks [J].Journal of Structural Geology,25(4): 515-528.
Hardy S and Finch E.2006.Discrete element modelling of the influence of cover strength on basement-involved fault-propagation folding [J].Tectonophysics,415(1-4): 225-238.
Hardy S,McClay K and Munoz J.2009.Deformation and fault activity in space and time in high-resolution numerical models of doubly vergent thrust wedges [J].Marine and Petroleum Geology,26(2): 232-248.
Hazzard J,Young R P and Maxwell S C.2000.Micromechanical modeling of cracking and failure in brittle rocks [J].Journal of Geophysical Research-Solid Earth,105(B7): 16683-16697.
Liu C,Pollard D D and Shi B.2013.Analytical solutions and numerical tests of elastic and failure behaviors of close-packed lattice for brittle rocks and crystals [J].Journal of Geophysical Research-Solid Earth,118: 71-82.
Mora P and Place D.1993.A lattice solid model for the non-linear dynamics of earthquakes [J].International Journal of Modern Physics C-Physics and Computers,4(6): 1059-1074.
Mora P and Place D 1994.Simulation of the frictional stick-slip instability [J].Pure and Applied Geophysics,143 (1-3): 61-87.
Mora P and Place D.1998.Numerical simulation of earthquake faults with gouge: toward a comprehensive explanation for the heat flow paradox [J].Journal of Geophysical Research-SolidEarth,103(B0): 21067-21089.
Place D and Mora P.1999.The lattice solid model to simulate the physics of rocks and earthquakes: Incorporation of friction [J].Journal of Computational Physics,150(2): 332-372.
Place D Lombard F,Mora P and Abe S.2002.Simulation of the microphysics of rocks using LSMearth [J].Pure and Applied Geophysics,159 (9): 1911-1932.
Potyondy D and Cundall P.2004.A bonded-particle model for rock [J].International Journal of Rock Mechanics and Mining Sciences,41(8): 1329-1364.
Shimizu H,Murata S and Ishida T.2011.The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution [J].International Journal of Rock Mechanics and Mining Sciences,48(5): 712-727.
Yin H,Zhang J,Meng L,et al.2009.Discrete element modeling of the faulting in the sedimentary cover above an active salt diapir [J].Journal of Structural Geology,31(9): 989-995.
Numerical Simulationof Hydraulic Fracturing Basedon Discrete Element Method
GU Yingfan1,LU Yi2,LIU Bing1,LIU Chun1,3*
1.School of Earth Sciences and Engineering,Nanjing University,Nanjing 210023,China; 2.Key Laboratory of Earth Fissures Geological Disaster,Ministry of Land and Resource,Geological Survey of Jiangsu Province,Nanjing 210049,China; 3.Nanjing University (Suzhou) High-tech Institute,Suzhou 215123,China
Abstract:The studies on the characteristics of hydraulic fracturing under different conditions have an important meaning to the effective shale gas exploration.As rocks are composed of grains and pores at micro scale,the discrete element method is introduced to simulate hydraulic fracturing processes.The rules of energy calculation and energy conversion in the models are proposed and a 3D discrete element model is built.Furthermore,3D discrete element numerical simulation software“MatDEM(3D)”is developed.The variations of strata stress and hydraulic speed are simulated by varying the model vertical strain and the particle diameters,respectively.The simulation results indicate: (1) the number and direction of hydraulic fractures are influenced by the anisotropic properties of rocks,stress state,and hydraulic speed.(2) Fractures are generated when the compressive wave passes.When hydraulic pressure increases at a high rate,the number of induced fractures is much greater.Furthermore,the percentage of effective energybook=195,ebook=198(fracturing energy) is also greater,and as a result,the efficiency of hydraulic fracturing is higher.(3) When the vertical strain is zero,50% of the fractures are vertical.When the vertical strain is -1×10(-4),the fractures tend to develop along the direction of the maximum compressive stress,and the percentages of vertical fractures are greater.The numerical simulation and energy analysis provide a new method for researching the hydraulic fracturing processes of rocks.
Key words:hydraulic fracturing; discrete element method; MatDEM; energy
*通讯作者:刘春,男,副教授,硕士生导师,长期从事计算工程地质方面研究;E-mail: chunliu@nju.edu.cn
作者简介:顾颖凡,男,硕士研究生,主要从事工程地质数值模拟方面研究;E-mail: guyingfan_nju@163.com
基金项目:国家自然科学基金青年项目(41302216);江苏省自然科学基金青年项目(BK20130377);江苏省科技支撑计划(BE2013115)资助
收稿日期:2015-11-20;修回日期:2016-02-15
DOI:10.16108/j.issn1006-7493.2015229
中图分类号:TE357.1
文献标识码:A
文章编号:1006-7493(2016)01-0194-06
Correpsponding author: LIU Chun,Associate Professor,E-mail: chunliu@nju.edu.cn

