构造物理模拟和PIV有限应变分析对构造裂缝预测的启示
沈礼,贾东,尹宏伟,魏东涛,陈竹新,孙闯,崔键.南京大学能源科学研究院,地球科学与工程学院,南京2002 2.中国石油天然气集团公司油藏描述重点实验室,兰州70020 .中国石油勘探开发研究院,北京0008 4.中国石油勘探开发研究院西北分院,兰州70020
构造物理模拟和PIV有限应变分析对构造裂缝预测的启示
沈礼1,2,贾东1*,尹宏伟1,魏东涛2,4,陈竹新3,孙闯1,崔键1
1.南京大学能源科学研究院,地球科学与工程学院,南京210023 2.中国石油天然气集团公司油藏描述重点实验室,兰州730020 3.中国石油勘探开发研究院,北京100083 4.中国石油勘探开发研究院西北分院,兰州730020
摘要:油气储层中构造裂缝发育与有限应变状态关系密切,为了探索有限应变分析与构造裂缝预测的新技术方法,此次研究设计完成了一组单侧挤压收敛模型的物理模拟实验,并引入粒子图像测速(PIV,Particle Image Velocimetry)技术对实验过程进行了定量化分析。实验模型在垂向上为含粘性层的多层结构,实验结果形成了一个肉眼可见的箱状褶皱。通过PIV技术可以获取实验模型变形演化过程中各阶段的位移场数据,计算出各阶段的增量应变,实现从初始状态到褶皱形成之后整个变形过程的有限应变分析,探讨构造裂缝成因机制和分布规律,进行定量化裂缝预测。挤压变形过程初期,应变分布范围很广,有限应变较弱(约4%~8 %),在挤压方向上的线应变表现为弱压应变,在垂向上的线应变表现为弱张应变,这种现象是褶皱和断层产生前平行层缩短和层增厚的纯剪变形结果,也是区域型张裂缝和剪裂缝形成的主要机制。褶皱和断层即将发育之时至发育之后,应变局限在断层发育的剪切带及附近区域,有限应变表现为较强(达20%)的剪切应变和剪切张应变,是断层面附近简单剪切变形作用的结果,也是局部型剪裂缝和张剪裂缝形成的主要机制。
关键词:物理模拟;粒子图像测速(PIV);有限应变分析;构造裂缝预测
1 引言
天然裂缝是储层中油气运移的重要通道,按成因可分为构造裂缝和非构造裂缝。构造裂缝的发育状况与构造事件相关联,包括与褶皱、断层等局部构造事件相关的裂缝和在弱构造变形区形成的裂缝(Nelson,1985);非构造裂缝的发育状况与构造作用无关,包括成岩裂缝、收缩裂缝以及与表面相关的裂缝(Lorenz,1991)。在致密储层中,裂缝控制着油气藏的分布(周新桂等,2003)。由于致密储层中非构造裂缝的孔径小、渗透率低以及横向连通性差等因素,构造裂缝成为了储层中主要的渗流通道,控制着储层中的油气成藏过程(王鹏威等,2014;曾联波等,2008;Zeng and Li,2009)。构造裂缝定量预测可以优化井位设置,对于油气藏开采具有指导意义。
构造裂缝定量预测的主要方法有:(1)构造主曲率法,该方法假设与挠曲有关的裂缝发生在构造面主曲率或倾角变化率极大处(曾锦光等,1982;Murray,1968)。(2)应力场数值模拟与岩石破裂法,利用有限元数值模拟确定地质模型中的应力分布,再根据岩石脆性破裂准则预测脆性破裂发生的位置(陈波和田崇鲁,1998;沈国华,2008;宋惠珍等,1999;文世鹏和李德同,1996)。(3)应变能法,通过计算地层中单位体积应变能来预测裂缝发育程度,该方法认为同样厚度的岩石中应变能越高,裂缝发育越多(郭迎春等,2010;Price,1966)。(4)统计学方法,通过统计学规律推测地下不同厚度岩层中裂缝间距的大小,该方法也适用于非构造裂缝(Narr,1991; Narr and Lerche,1984)。构造裂缝的成因和影响因素很多,每种方法的依据可能只是裂缝的一种成因机制或分布规律,所以研究者们也会综合利用多种方法来进行构造裂缝预测(丁中一等,1998;高帅等,2015;周新桂等,2007),预测效果较之单一方法有所改善,但仍然存在一些局限,还不能够全面地解决构造裂缝定量预测问题。
本文以物理模拟实验和粒子图像测速(PIV)技术为基础,从构造裂缝发育和有限应变状态的关系出发,探索构造裂缝定量预测的新技术方法。物理模拟实验可以提供褶皱、断层等构造发育形成过程的真实可见物理模型(Koyi,1997)。运用PIV技术可以实现对模型中构造发育演化过程的定量监测(沈礼等,2012;Adam et al.,2005),分析构造变形发育之前和形成之后的有限应变状态,再结合构造裂缝发育与有限应变状态的关系进行定量化构造裂缝预测。
2 构造物理模拟实验
2.1实验模型
本文旨在探索有限应变分析和构造裂缝预测的新技术方法,因此在进行构造物理模拟时设计了较为简单的实验模型。实验模型的初始尺寸为长600 mm(x方向)、宽400 mm(y方向)、厚45 mm (z方向)。为了考察粘性层上下变形的差异,模型垂向上设计为含粘性层的多层结构。模型底部设置了5 mm厚的微玻璃珠以减少基底摩擦力,使构造变形更容易沿基底滑脱面向前传递。底部微玻璃珠之上从底面往顶面依次设置了17 mm厚的石英砂、5 mm厚的硅胶(靠近挤压端一段为微玻璃珠)和18 mm厚的石英砂(图1)。
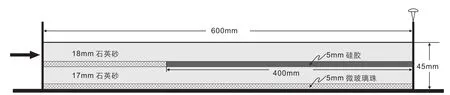
图1 实验模型剖面示意图Fig.1 Schematic diagram of the experimental model
实验模型中部设置的硅胶是一种粘度系数为1×104Pa·s的粘性材料,变形规律符合牛顿流体变形规则,是模拟自然界岩盐层、膏岩层等软弱滑脱层的理想材料(Bonini,2007;Costa and Vendeville,2002)。脆性材料石英砂和微玻璃珠的变形遵循莫尔-库仑破裂准则,具有较小的内聚强度,石英砂内摩擦角约30°,微玻璃珠内摩擦角约25°,都是模拟地壳脆性变形的理想材料(Cotton and Koyi,2000;Massoli et al.,2006)。为了提高PIV计算识别精度,实验中使用了颗粒感更加明显的杂色石英砂,由白色石英砂和彩色石英砂均匀混合而成。实验中还采用彩色石英砂设置了标志层以便于观察模型的变形情况,硅胶层之下用红色石英砂作标志层,硅胶层之上用绿色石英砂作标志层。不同颜色石英砂的力学性质是一致的。实验材料的具体物理性质参数见表1。
实验动力来源为x方向上的单侧挤压,挤压总缩短量为18 mm,缩短速率为0.0015 mm/s。实验过程中,侧面相机每隔5分钟拍摄一幅剖面彩色图像,PIV系统的高精度CCD镜头每隔两分钟采集一幅剖面灰度图像。
2.2模型相似性
表1中列出了实验模型和自然界原型中的各物理量参数以及通过这些参数计算出来的相似比例参数。实验模型与自然界原型的几何学相似性由实验模型与自然界原型的长度相似比例给出:

表1 材料物理性质及模型相似性参数Tab.1 Parameters of the materials and the scaling of the model
l*=2.5×10-6(即实验中1 cm代表自然界4 km)
动力学相似性由应力相似比例给出,根据Hubbert(1937)最早提出的相似理论,应表示为:
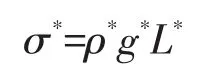
其中,ρ*表示密度相似比例,g*表示重力加速度相似比例。实验中所用材料与自然界岩石的密度相似比例ρ*≈0.54,实验在正常重力加速度场中进行,所以重力加速度相似比例g*=1。因此,模型与自然界原型的应力相似比例σ*= 1.4×10-6。设自然界滑脱层粘度系数为1×1019Pa·s(Bonini,2007;Cotton and Koyi,2000;Couzens-Schultz et al.,2003;Leturmy et al.,2000),那么模型与自然界原型的粘度系数相似比例η*=1×10-15,因此,模型与原型之间的应变速率相似比例:
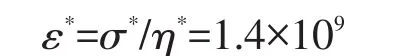
时间相似比例是应变速率相似比例的倒数,所以时间相似比例t*=7.1×10-10,即实验中的1小时代表了自然界的0.16 Ma,本文实验挤压过程耗时200分钟,代表了自然界中的0.53 Ma。运动学相似性由实验模型与自然界原型的缩短速率相似比例给出:
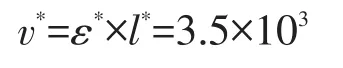
因此,实验中推挤速率0.0015 mm/s就代表了自然界缩短速率为14 mm/a。
2.3实验结果及讨论
实验模型变形演化过程如图2所示,挤压缩短量s从0 mm增加到5.4 mm的过程中,模型物质沿基底滑脱面向前传递,但剖面上并没有明显的变形(图2a-c)。当挤压缩短量达到8.1 mm时,模型物质发生了微弱的形变(图2d)。当挤压缩短量达到10.8mm时,靠近挤压端的位置形成了一个箱状褶皱,形态由一对共轭的剪切带所控制(图2e)。挤压缩短量从10.8 mm增加到18.0 mm的过程中,箱状褶皱沿共轭剪切带继续发育、抬升,剪切带宽度明显减小(图2f)。整个实验过程中,粘性层上下未见明显变形。
实验模型挤压缩短过程中形成的箱状褶皱亦可以描述为断层端点褶皱,其演化过程从初始阶段的平行层缩短开始,接着产生沿基底滑脱面滑动的滑脱褶皱,最后形成断层端点褶皱(Bernard et al.,2007;Storti et al.,1997)。这与本文实验中观察到的现象是一致的。如果缩短量继续增加,断面所在的剪切带将逐渐变窄,模型最后将演化为断层断坡褶皱(Storti et al.,1997)。对物理模拟实验中这类现象的进一步分析可以让构造地质学家更深入地理解断层相关褶皱运动学演化过程,帮助复杂地震数据的解释和构造演化的平衡恢复((Daeron et al.,2007;Simoes et al.,2007))。本文接下来将运用PIV技术分析实验模型中褶皱、断层(剪切带)产生前、后的有限应变状态,探讨油气储层中构造裂缝的形成机制和分布规律。
3 粒子图像测速(PIV)技术
3.1 PIV工作的基本原理
粒子图像测速,英文为ParticleImageVelocimetry,通常简称为PIV。该测速技术最初是在流体力学实验的研究领域发展起来的(Adrian,1991),后被引入到岩土工程实验中计算颗粒材料的位移和变形情况(White et al.,2003;Wolf et al.,2003),最近十年才被应用到构造物理模拟实验中定量化监测实验模型的构造演化过程(Adam et al.,2005)。与物理模拟实验传统分析方法相比,PIV技术既节省时间又能提高位移变形监测的时间、空间分辨率和精准度(至少一个数量级以上),所以近年来被广泛地应用到物理模拟实验中分析诸如应变集中过程(Boutelier et al.,2014;Dooley et al.,2015;Leever et al.,2011;Santimano et al.,2015)、地表过程(Cruz et al.,2008;Reiter et al.,2011;Wu et al.,2015)、地震活动(Knap⁃pett et al.,2006;Rosenau et al.,2009)以及断层的粘滑运动(Yamadaet al.,2006)等地质过程。值得一提的是,与PIV技术工作原理类似的数字图像相关(DIC,Digital Image Correlation)技术与光学流动技术(Optical Flow Technique)也经常被应用到物理模拟实验中监测模型的运动和变形过程(Bernard et al.,2007;Bonini et al.,2015;Grave⁃leau et al.,2008;Hall et al.,2010)。
PIV技术是一种可以实现非线性位移变形可视化的光学、非接触式图像相关技术。其工作的基本原理如图3,通过PIV系统高分辨率镜头获取实验模型变形过程中的一系列灰度图像(图3A),每幅图像都可以用对应的灰度坐标函数表示,不同图像函数可以通过互相关函数联系起来。将时间间隔为dt的两幅图像划分为多个问询域(图3B),通过基于快速傅里叶变化的互相关运算可以计算出局部问询域内颗粒在dt时间内的位移,而互相关函数的峰值代表了局部问询域内颗粒的平均位移(图3C)。这样每个问询域都获得了一个位移矢量,所有问询域的位移矢量就构成了整幅图像在dt时间内的位移矢量场。对于位移和变形比较大的地方,通过逐步缩小问询域的迭代算法和变形窗口算法可以提高位移矢量的空间分辨率(Fincham and Spedding,1997;Scarano and Riethmuller,2000;Wieneke,2001)。以增量位移矢量为基础,便可以进一步获取模型的增量应变,如线应变、剪切应变和面积应变等。将每个阶段的增量应变按顺序求和,也就获得了模型变形演化过程中的有限应变状态。
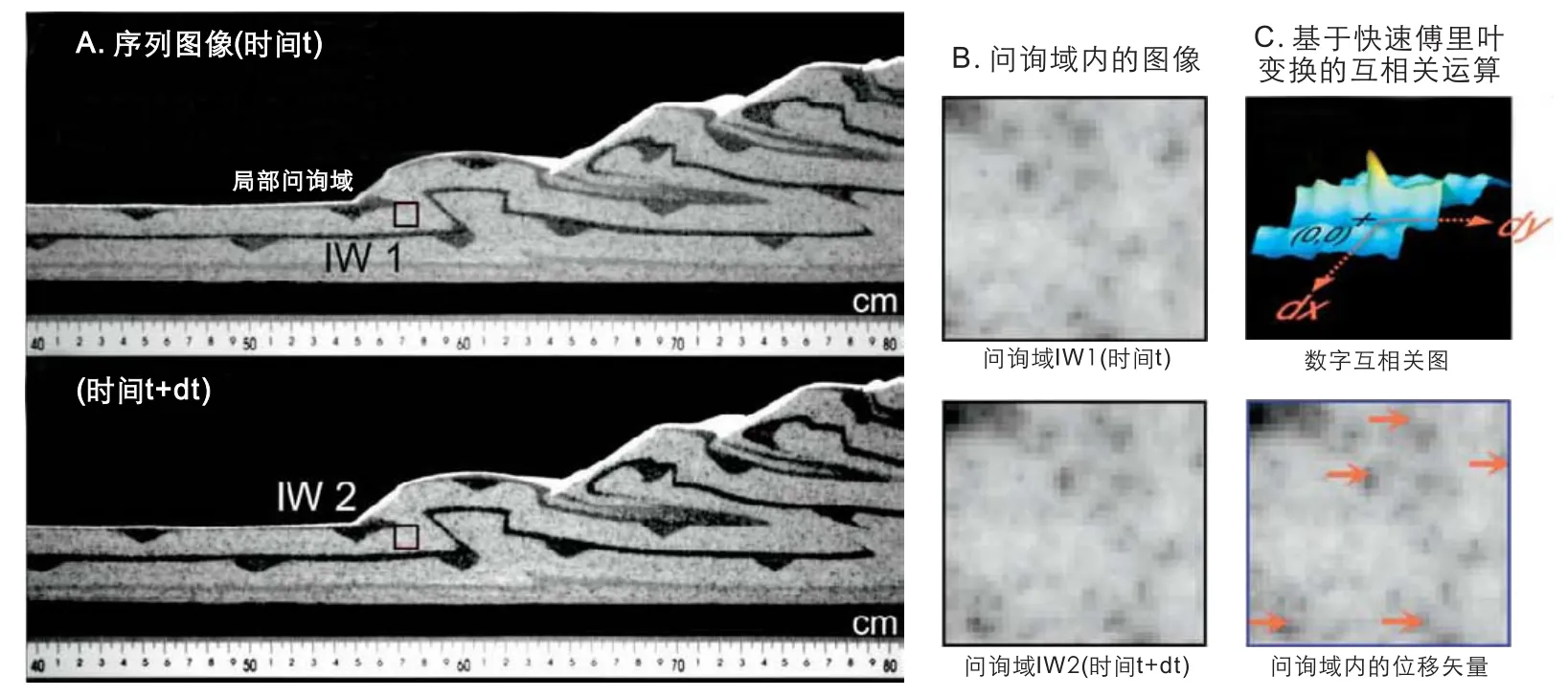
图3 PIV技术工作基本原理Fig.3 Fundamental of PIV technique (modified after Adam et al.,2005)
3.2 PIV计算结果的精度
PIV计算位移矢量数据的空间分辨率由PIV系统数字镜头的光学分辨率和互相关算法的精度决定(Adam et al.,2005)。普通的四百万像素数码相机照片就能够满足PIV分析的需求,但是其采集的图像通常为彩色图像,而在进行PIV互相关运算前必须转换为灰度图像,这个转换和压缩过程将会损失部分图像信息,降低PIV分析的精度。PIV系统的镜头可以直接采集灰度图像,比较完整的保留图像的灰度梯度。根据前人的研究,PIV系统计算的位移矢量标准差小于0.1个像素(White et al.,2003)。本文采用的PIV分析系统为北京立方天地科技发展有限责任公司所开发,其技术报告中对人工旋转场粒子图像的计算结果进行了误差分析,用实例证明了其计算结果的标准差小于0.1像素。本文PIV系统的CCD(Charge-coupled Device)镜头光学分辨率为四百万像素(2048×2048),用于PIV计算分析的实验模型长度为42 cm,所以本文计算结果位移矢量长度的空间分辨率为0.02 mm。应变测量的相对误差与问询域的尺寸和计算区域重叠率相关,本文在进行互相关计算时采用的问询域大小为16× 16像素,步长为12×12像素,重叠率为75%,计算结果相对误差小于1%。时间分辨率受限于数字镜头采集图像的频率(帧转移的速度),普通的数码相机采集图像时需要对图像进行压缩,采集频率大约为0.1 Hz,而本文PIV系统的CCD数字镜头采集图像时不需要对图像进行压缩,采集频率最大可达8 Hz,并且还不会丢失图像信息。
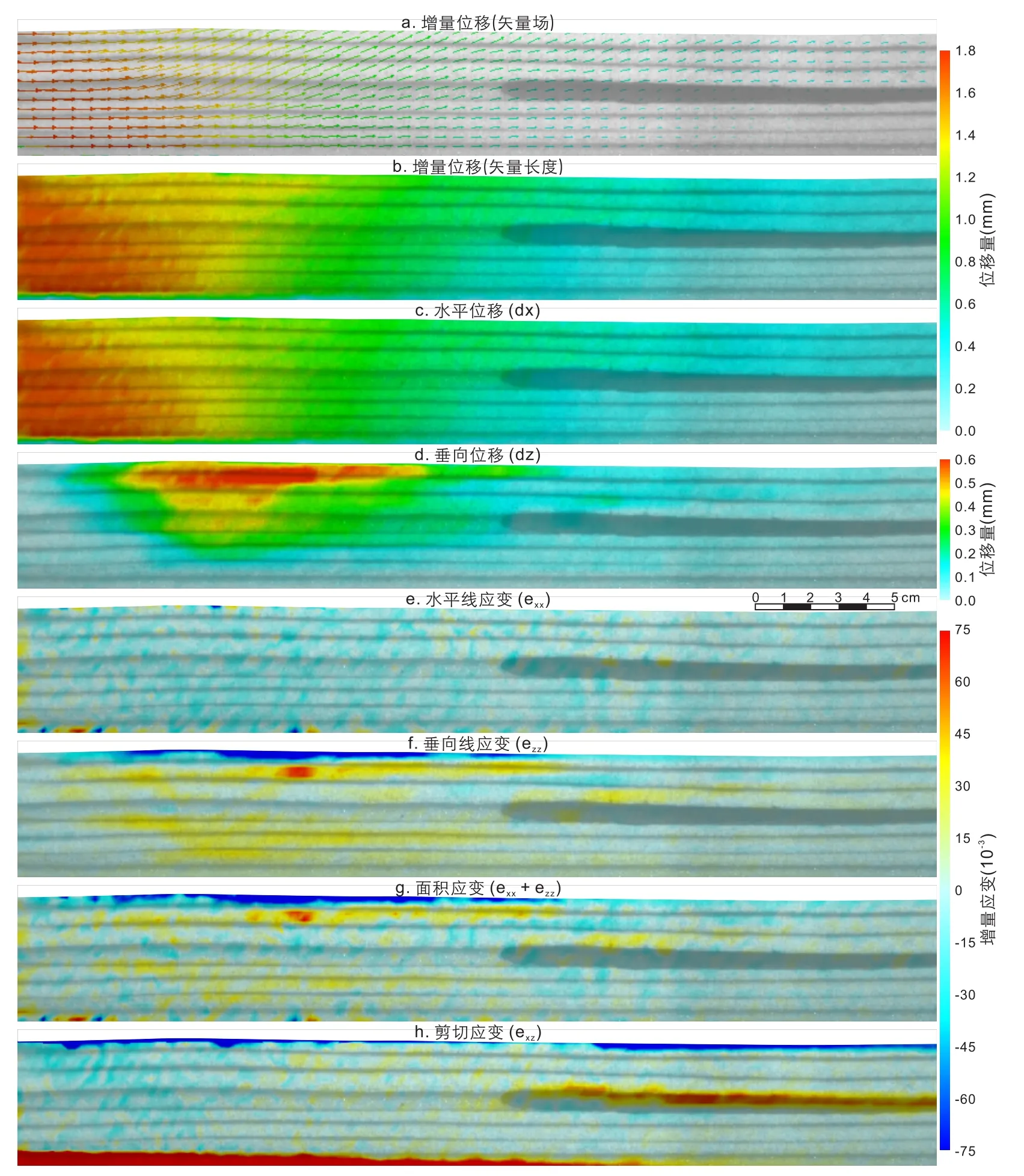
图4 褶皱发育前的增量位移和增量应变状态(底图对应图2 c)Fig.4 Incremental displacement field and incremental strain state before the fold initiated (Background corresponding to Fig.2c)
3.3褶皱发育前后的增量应变分析
增量位移量和总的位移量数据可以提供实验模型整个构造变形过程的应变演化历史。图4a展示了实验模型褶皱发育前(实验时间t从60分钟到80分钟,dt=20分钟;缩短量s从5.4 mm到7.2 mm,ds=1.8 mm)的增量位移矢量场,底图为实验进行到60分钟,缩短量为5.4 mm时的图像(图2c)。图4b是根据位移矢量长度所成的增量位移彩色云图,右侧的色标给出了每种颜色代表的具体位移量。在靠近挤压端的位置,增量位移矢量场显示出一个斜边并不十分明显的红色直角三角区域,其位移方向与实验模型挤压缩短方向一致,且位移量大小约为1.8 mm,与模型挤压端的缩短量相当。在这个斜边的右侧,位移矢量方向几乎均为右上方向,仅在底面附近和粘性层右端表现为纯向右,这在水平位移量(图4c)和垂向位移量(图4b)的分布范围上也可以表现出来。紧挨着红色直角三角区,呈现出一个倒立的黄色等腰三角区,位移量约1.3 mm,再往右是一个近似平行四边形的绿色区域,位移量约0.8~1.0 mm。继续向右来到模型前端含粘性层的地方,可以发现位移量在粘性层之上比之下覆盖范围更大,但位移量都小于0.6 mm。位移场在模型剖面上表现出了从挤压端向前逐渐减小的梯度。
增量应变可以根据增量位移场计算出来,本文主要分析了与构造裂缝预测相关的水平线应变(exx)、垂向线应变(ezz)、面积应变(exx+ezz)和剪切应变分量(exz)。褶皱发育之前,水平线应变、垂向线应变和面积应变都比较分散,分布范围都很广,没有表现出应变集中的位置,也都较弱,大小约为3%~4 %(图4e-g)。水平线应变为弱压应变,垂向线应变为弱张应变,面积应变既有张应变也有压应变,规律性不强。剪切应变则主要集中在底面和粘性层面之上,强度较大,均大于7.5 %(图4h)。
褶皱发育之后(实验时间t从180分钟到200分钟,dt=20分钟;缩短量s从16.2 mm到18.0 mm,ds=1.8 mm),靠近挤压端的直角三角区域增量位移大小和方向都仍与挤压端一致,斜边边界更加清晰,对应反冲断层(BT)所在的位置,右侧倒立等腰三角区域位移方向为右上方向,位移大小在1.5 mm左右,前冲断层(FT)所在的剪切带位移明显减小约为0.8~1.0 mm,前冲断层下盘位移全部为零(图5a-d)。褶皱发育之后增量位移梯度非常明显,增量应变也几乎全部集中在前冲断层和反冲断层所在的剪切带位置,前冲断层所在剪切带应变强度明显强于反冲断层所在剪切带(图5e-h)。
增量应变分析显示,紧挨着模型挤压端的直角三角区域在褶皱发育前后都与模型挤压端的位移保持一致,也几乎没有内部应变,它的作用可以等同于不变形的后挡板。褶皱发育前后最明显的区别在于褶皱发育前应变比较分散,分布范围大,强度较弱;而褶皱发育后应变主要集中在反冲断层和前冲断层附近的剪切带,强度较大。从应变产生的机制上,褶皱发育前位移梯度主要靠平行层缩短和层增厚吸收,应变属于纯剪切变形的结果;而褶皱发育后位移梯度明显反应出两条剪切带的活动,应变属于简单剪切变形的结果。另外,模型底面和粘性层面与其上覆层之间的剪切应变也应该属于简单剪切变形的结果。
4 有限应变分析
实验模型变形全过程的有限应变是所有间断过程增量应变的总和。本文实验过程中,PIV系统每隔2分钟采集一次图像,便可以计算一次增量位移和增量应变。由于实验模型从褶皱发育之时至实验结束的过程中,变形方式几乎没有发生变化,所以本文仅选取了模型初始状态到褶皱发育之后(实验进行时间为120分钟时)的过程进行了有限应变分析。图6-8展示了这120分钟内实验模型剖面变形总位移量和有限应变的累积过程,即60个连续间断过程(dt=2分钟)增量位移和增量应变的累加过程。
实验模型剖面变形位移量累积过程显示,实验从初始状态到挤压缩短量为8.1mm的过程中,累积位移量在剖面上大部分地方均逐渐增加(图6a-d),而在挤压缩短量从8.1 mm增加至10.8 mm的过程中,累积位移量只在前冲断层左侧区域增加,这说明在前冲断层即将发育之时至发育之后,其下盘的位移量就不再增加。在靠近挤压端的直角三角区域内累积位移量始终与挤压缩短量保持大致相等(图6e),说明该区域内的物质在整个过程中都与挤压端的运动基本一致。
有限剪切应变的累积过程显示,挤压缩短量达到8.1 mm之前,有限剪切应变的分布比较广泛,应变强度随着挤压缩短过程逐渐增大(图7a-d)。但除了在粘性层所在位置较为集中,强度较大(在挤压缩短量为8.1 mm时约20%)外,其余地方都较弱(在挤压缩短量为8.1 mm时约4%)。在挤压缩短量从8.1 mm增加至10.8 mm的过程中,有限剪切应变在前冲断层所在位置增加最为明显,强度达到20%,前冲断层左侧区域有限剪切应变只有少量增加,而其下盘有限剪切应变完全没有增加(图7e)。有限面积应变累积过程显示,在挤压缩短量达到8.1 mm之前,剖面上有限面积应变在比较宽广的区域内逐渐增大,且有向模型前端(右侧)扩展的趋势,最远可以到达离挤压端约30 cm处,但有限面积应变的强度较弱,在挤压缩短量为8.1 mm时约4%~8 %(图8a-d)。另外,分散的有限面积应变还出现了一定程度的分层现象。挤压缩短量从8.1 mm增加到10.8 mm的过程中,有限面积应变在前冲断层左侧有少量增加,在反冲断层和前冲断层所在位置及邻近区域增加比较明显。在缩短量为10.8 mm时,有限面积应变强度在反冲断层及附近位置约为12 %,在前冲断层及附近位置达±20 %(图8e)。
结合本文前一部分对褶皱发育前后的增量应变分析,我们可以认识到,从初始状态到褶皱发育形成之后的整个过程中,分布广泛的有限应变主要来源于褶皱发育之前,强度较弱;分布较为集中的有限应变主要来源于褶皱和断层即将发育之时至发育之后,主要集中在断层及邻近区域,强度较大。贾东等(2007)在采用磁组构方法研究断层相关褶皱有限应变状态的工作中也得到了相同的认识。说明褶皱和断层的发育过程中地层经历了从分散应变到应变集中这两种变形方式(Adam et al.,2005;Bernard et al.,2007)。分散应变主要反映了纯剪切变形造成的平行层缩短和层增厚过程,应变集中主要反映的是断层及附近位置的简单剪切变形过程。另外,粘性层所在位置集中的有限剪切应变反映了粘性层之上的变形比粘性层之下的变形传递得更远,是粘性层上下简单剪切变形的结果。
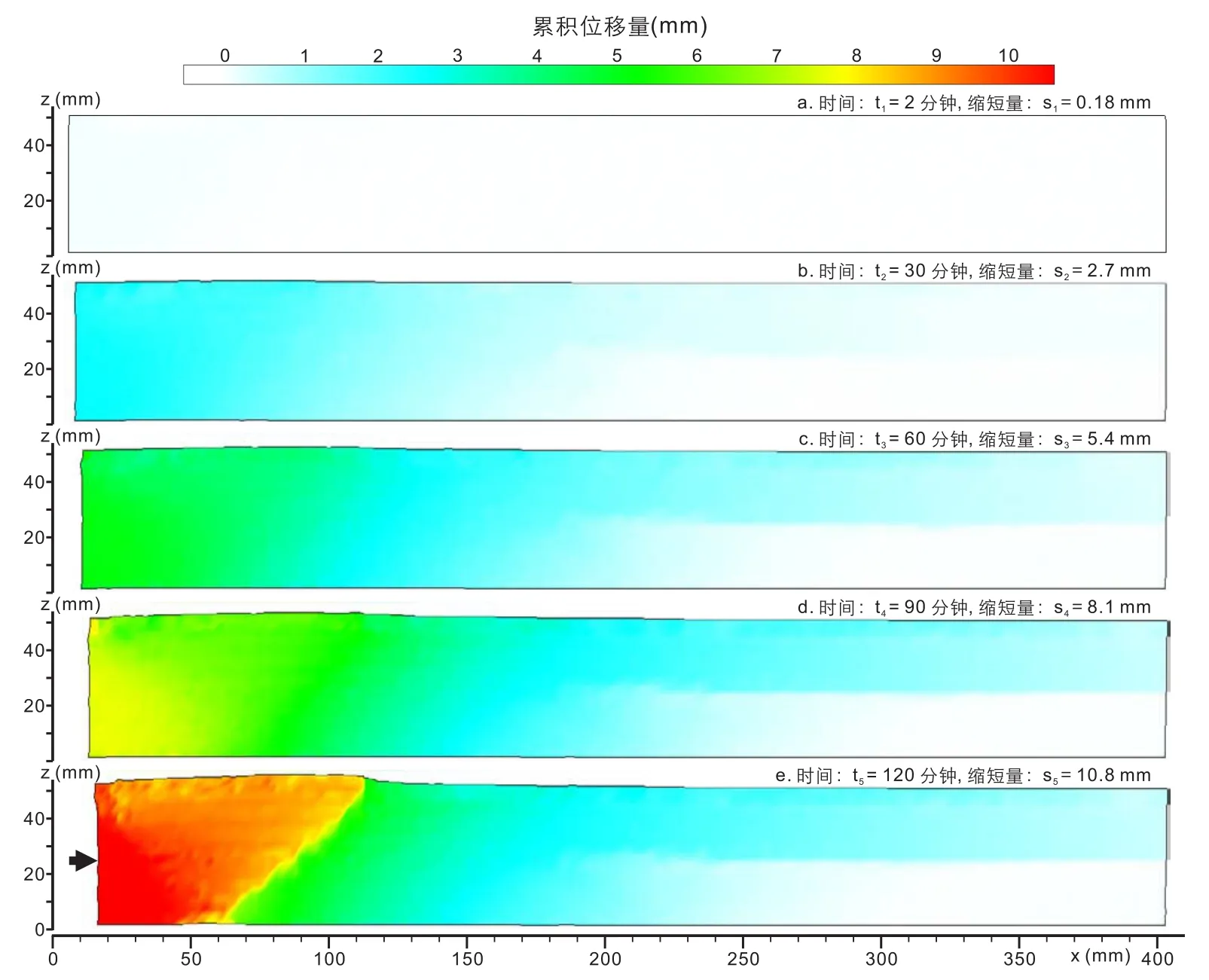
图6 总位移量的累积过程Fig.6 Cumulative process of the total displacement
5 构造裂缝预测与展望
天然裂缝按成因机制可分为构造裂缝和非构造裂缝两大类(Lorenz,1991;Nelson,1985)。按裂缝性质可以分为与应变能相关的剪裂缝、与岩层褶皱相关的张裂缝以及与断层相关的剪裂缝和张剪裂缝(McQuillan,1973;Murray,1968;Price,1966)。秦启荣和苏培东(2006)以构造裂缝预测为目的,依据构造裂缝的形成方式、空间分布以及与构造运动的时间关系将其进一步划分为区域型、局部型和复合型构造裂缝3大类。
本文通过物理模拟实验模拟了褶皱和断层构造发育的整个过程,并运用PIV技术实现了整个过程的有限应变分析,分析结果可以用来探讨构造裂缝的成因机制和分布规律。在挤压变形初始阶段褶皱和断层尚未开始发育之前,地层中广泛地分布着纯剪切变形作用引起的弱应变,其分布范围在挤压方向上可达120 km(模型中30 cm),是构造事件初期分布广泛的区域型张裂缝和剪裂缝形成的主要机制。在褶皱和断层即将发育之时至发育之后,有限应变主要集中在断层所在位置及邻近区域,应变强度较大,是断层面附近简单剪切变形作用的结果,也是局域型剪裂缝和张剪裂缝发育的主要机制。另外,褶皱和断层发育之前产生的分布式有限面积应变出现的分层现象,很有可能反映了区域型水平张裂缝的成层发育状况,但也有可能与PIV系统对本文实验模型中彩色石英砂标志层的识别有关。
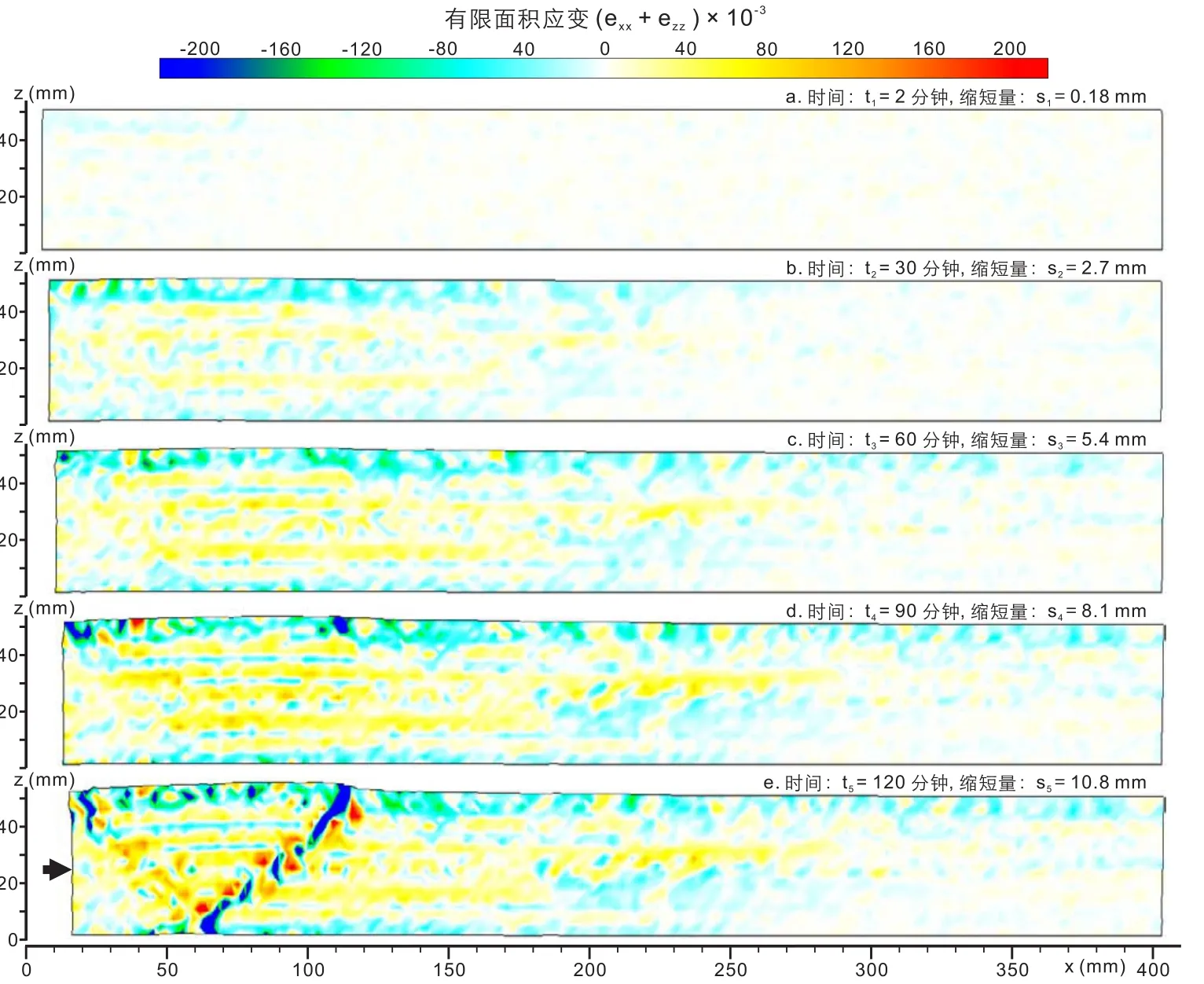
图8 有限面积应变的累积过程Fig.8 Cumulative process of the finite area strain
裂缝发育程度与有限应变强度有关,构造事件初期地层中广泛分布的弱应变约为4%~8%,这些应变若全部反映为张裂缝,那么储层中的油气储集空间将大大增加,尤其对于致密储层,这样的变化甚至可以改变储层的性质,其很有可能演化为比较好的储层。分布在断层面附近的强应变达20 %,这些应变反映的剪裂缝和张剪裂缝在断层活动时期可以作为油气运移的通道,而在断层不活动的时期则可能起到封堵作用。
以物理模拟实验和PIV技术为基础,定量分析褶皱和断层构造发育过程中有限应变演化历史,通过有限应变状态与构造裂缝发育的关系,探讨裂缝成因机制和分布规律,是实现构造裂缝定量预测的一种切实可行的办法。本文定量地分析了构造发育前后的有限应变状态,探讨了构造裂缝的成因机制和分布规律,但还没有具体地给出有限应变状态与构造裂缝发育程度之间的定量关系,所以还有很多方面值得改进。比如,将本文研究结果与实际研究区域的地面裂缝、钻井岩芯裂缝发育情况的统计结果结合起来可以为研究有限应变状态与构造裂缝发育程度之间的定量关系提供线索;有限元数值模拟(Maerten and Maerten,2006)和离散元数值模拟(尹宏伟等,未发表成果)进行实验模型应力应变分析的方法也可以与本文物理模拟实验有限应变分析的方法结合起来进行构造裂缝的定量预测;利用CT扫描和数字体相关(DVC,Digital Volume Correlation)技术进行物理模拟实验的三维有限应变分析(Adam et al.,2013)可以实现三维构造裂缝定量预测。
参考文献(References):
陈波,田崇鲁.1998.储层构造裂缝数值模拟技术的应用实例[J].石油学报,19(4): 50-54.
丁中一,钱祥麟,霍红,等.1998.构造裂缝定量预测的一种新方法——二元法[J].石油与天然气地质,19(1): 1-7,14.
高帅,曾联波,马世忠,等.2015.致密砂岩储层不同方向构造裂缝定量预测[J].天然气地球科学,26(3): 427-434.
郭迎春,薛峰,汪必峰.2010.储层应力应变与裂缝体积密度定量关系研究[J].油气地质与采收率,17(4): 87-90.
贾东,陈竹新,罗良,等.2007.断层相关褶皱的磁组构与有限应变:川西岷江冲断构造的实例分析[J].自然科学进展,17(2): 188-195.
秦启荣,苏培东.2006.构造裂缝类型划分与预测[J].天然气工业,26 (10): 33-36.
沈国华.2008.有限元数值模拟方法在构造裂缝预测中的应用[J].油气地质与采收率,15(4): 24-29.
沈礼,贾东,尹宏伟,等.2012.基于粒子成像测速(PIV)技术的褶皱冲断构造物理模拟[J].地质论评,58(3): 471-480.
宋惠珍,曾海容,孙君秀,等.1999.储层构造裂缝预测方法及其应用[J].地震地质,21(3): 205-213.
王鹏威,陈筱,庞雄奇,等.2014.构造裂缝对致密砂岩气成藏过程的控制作用[J].天然气地球科学,25(2): 185-191.
文世鹏,李德同.1996.储层构造裂缝数值模拟技术[J].石油大学学报(自然科学版),20(5): 17-24.
曾锦光,罗元华,陈太源.1982.应用构造面主曲率研究油气藏裂缝问题[J].力学学报,(2): 202-206.
曾联波,高春宇,漆家福,等.2008.鄂尔多斯盆地陇东地区特低渗透砂岩储层裂缝分布规律及其渗流作用[J].中国科学(D辑),38(增刊I):41-47.
周新桂,操成杰,袁嘉音.2003.储层构造裂缝定量预测与油气渗流规律研究现状和进展[J].地球科学进展,18(3): 398-404.
周新桂,张林炎,范昆.2007.含油气盆地低渗透储层构造裂缝定量预测方法和实例[J].天然气地球科学,18(3): 328-333.
Adam J,Klinkmüller M,Schreurs G,et al.2013.Quantitative 3D strain analysis in analogue experiments simulating tectonic deformation: Integration of X-ray computed tomography and digital volume correlation techniques [J].Journal of Structural Geology,55: 127-149.
Adam J,Urai J L,Wieneke B,et al.2005.Shear localisation and strain distribution during tectonic faulting--new insights from granular-flow experiments and high-resolution optical image correlation techniques [J].Journal of Structural Geology,27: 283-301.
Adrian R J.1991.Particle-imaging techniques for experimental fluid mechanics [J].Annual Review of Fluid Mechanics,23: 261-304.
Bernard S,Avouac J-P,Dominguez S,et al.2007.Kinematics of fault-related folding derived from a sandbox experiment [J].Journal of Geophysical Research,112,B03S12,doi: 10.1029/2005JB004149.
Bonini M.2007.Deformation patterns and structural vergence in brittle-ductile thrust wedges: An additional analogue modeling perspective [J].Journal of Structural Geology,29: 141-158.
Bonini L,Basili R,Toscani G,et al.2015.The role of pre-existing discontinuities in the development of extensional faults: An analog modeling perspective [J].Journal of Structural Geology,74: 145-158.
Boutelier D,Oncken O and Cruden A R.2014.Trench-parallel shortening in the forearc caused by subduction along a seaward-concave plate boundary: Insights fromanalogue modelling experiments [J].Tectonophysics,611(1): 192-203.
Costa E and Vendeville B C.2002.Experimental insights on the geometry and kinematics of fold-and-thrust belts above weak,viscous evaporitic decollement [J].Journal of Structural Geology,24: 1929-1739.
Cotton J T and Koyi H A.2000.Modeling of thrust fronts above ductile and frictional detachments: Application to structures in the Salt Range and Potwar Plateau,Pakistan [J].Geological Society of America Bulletin,112(3): 351-363.
Couzens-Schultz B A,Vendeville B C and Wiltschko D V.2003.Duplex style and triangle zone formation: insights from physical modeling [J].Journal of Structural Geology,25: 1623-1644.
Cruz L,Teyssier C,Perg L,et al.2008.Deformation,exhumation,and topography of experimental doubly-vergent orogenic wedges subjected to asymmetric erosion [J].Journal of Structural Geology,30: 98-115.
Daeron M,Avouac J-P and Charreau J.2007.Modeling the shortening history of a fault tip fold using structural and geomorphic records of deformation [J].Journal of Geophysical Research,112,B03S13,doi: 10.1029/2006JB004460.
Dooley T P,Jackson M P A,Jackson C A-L,et al.2015.Enigmatic structures within salt walls of the Santos Basin-Part 2: Mechanical explanation from physical modelling [J].Journal of Structural Geology,75: 163-187.
Fincham A M and Spedding G R.1997.Low cost high resolution DPIV for measurement of turbulent fluids [J].Experiments in Fluids,23: 449-462.
Graveleau F and Dominguez S.2008.Analogue modelling of the interactions between tectonics,erosion and sedimentation in foreland thrust belts [J].Comptes Rendus Geoscience,340(5): 324-333.
Hall A S,Wood D W,Ibraim E,et al.2010.Localised deformation patterning in 2D granular materials revealed by digital image correlation [J].Granular Matter,12: 1-14.
Hubbert M K.1937.Theory of scale models as applied to the study of geologic structure [J].Geological Society of America Bulletin,48(10): 1459-1519.
Knappett J A,Haigh S K and Madabhushi S P G.2006.Mechanisms of failure for shallow foundations under earthquake loading [J].Soil Dynamics and Earthquake Engineering,26: 91-102.
Koyi H.1995.Mode of internal deformation in sand wedges [J].Journal of Structural Geology,17: 293-300.
Koyi H.1997.Analogue modeling: from a qualitative to a quantitative technique--a historical outline [J].Journal of Petroleum Geology,20(2): 223-238.
Leever K A,Gabrielsen R H,Sokoutis D,et al.2011.The effect of convergence angle on the kinematic evolution of strain partitioning in transpressional brittle wedges: Insight from analog modeling and highresolution digital image analysis [J].Tectonics,30(2): 182-187.
Leturmy P,Mugnier J L and Vinour P.2000.Piggyback basin development above a thin-skinned thrust belt with two detachment levels as a function of interactions between tectonic and superficial mass transfer: the case of the Subandean Zone (Bolivia) [J].Tectonophysics,320: 45-67.
Lorenz J C,Lawrence W T and Warpinski N R.1991.Regional fractures I: a mechanism for the formation of regional fractures at depth in flat-lying reservoirs [J].AAPG Bulletin,75(11): 1714-1737.
Maerten L and Maerten F.2006.Chronologic modeling of faulted and fractured reservoirs using geomechanically based restoration: Technique and industry applications [J].AAPG Bulletin,90(8): 1201-1226.
Massoli D,Koyi H A and Barchi M R.2006.Structural evolution of a fold and thrust belt generated by multiple decollement: analogue models and natural examples from the Northern Apennines (Italy) [J].Journal of Structural Geology,28: 185-199.
McQuillan H.1973.Small-scale fracture density in Asmari formation of southwest Iran and its relation to bed thickness and structural setting [J].AAPG Bulletin,57(4): 2367-2385.
Murray Jr G H.1968.Quantitative Fracture Study--Sanish Pool,Mckenzie County,North Dakota [J].AAPG Bulletin,52(1): 57-65.
Narr W.1991.Fracture density in the deep subsurface: techniques with application to Point Arguello Oil Field [J].AAPG Bulletin,75(8): 1300-1323.
Narr W and Lerche L.1984.A method for estimating subsurface fracture density in core [J].AAPG Bulletin,68(5): 637-648.
Nelson R A.1985.Geologic Analysis of Naturally Fractured Reservoirs [M].Houston,Texas: Gulf Publishing Company: 1-320.
Price N J.1966.Fault and Joint Development in Brittle and Semi-Brittle Rock [M].Oxford: Pergamon Press: 1-176.
Reiter K,Kukowski N and Ratschbacher L.2011.The interaction of two indenters in analogue experiments and implications for curved fold-and-thrust belts [J].Earth and Planetary Science Letters,302: 132-146.
Rosenau M,Lohrmann J and Oncken O.2009.Shocks in a box: An analogue model of subductionearthquake cycles withapplicationto seismotectonic forearc evolution [J].Journal of Geophysical Research Atmospheres,114(B1): 10361.
Santimano T,Rosenau M and Oncken O.2015.Intrinsic versus extrinsic variability of analogue sand-box experiments-Insights from statistical analysis of repeated accretionary sand wedge experiments [J].Journal of Structural Geology,75: 80-100.
Scarano F and Riethmuller M L.2000.Advances in iterative multigrid PIV image processing [J].Experiments in Fluids,29: 51-60.
Simoes M,Avouac J P,Chen Y G,et al.2007.Kinematic analysis of the Pakuashan fault tip fold,west central Taiwan: Shortening rate and age of folding inception [J].Journal of Geophysical Research,112,B03S14,doi: 10.1029/2005JB004198.
Storti F,Salvini F and McClay K.1997.Fault-related folding in sandbox analogue models of thrust wedges [J].Journal of Structural Geology,19: 583-602.
White D J,Take W A and Bolton M D.2003.Soil deformation measurement using particle image velocimetry (PIV) and photogrammetry [J].Geotechnique,53(7): 619-631.
Wieneke B.2001.PIV adaptive multi-pass correlation with deformed interrogation windows [J].PIV Challenge,2001: 1-6.
Wolf H,Konig D and Triantafyllidis T.2003.Experimental investigation of shear band patterns in granular material [J].Journal of Structural Geology,25: 1229-1240.
Wu J E,Mcclay K and Frankowicz E.2015.Niger Delta gravity-driven deformation above the relict Chain and Charcot oceanic fracture zones,Gulf of Guinea: Insights from analogue models [J].Marine & Petroleum Geology,65: 43-62.
Yamada Y,Baba K and Matsuoka T.2006.Analogue and numerical modeling of accretionary prisms with a decollement in sediments [G].In: Buiter S J H,Schreurs G.eds.Analogue and Numerical Modelling of Crustal-ScaleProcesses.Geological Society,London,Special Publications,253: 169-183.
Zeng L B and Li XY.2009.Fractures in sandstone reservoirs with ultra-low permeability: A case study of the Upper Triassic Yanchang Formation in the Ordos Basin,China [J].AAPG Bulletin,93(4): 461-477.
Structural Analogue Modelingand PIVFinite Strain Analysis: Implicationsto Tectonic Fracture Prediction
SHEN Li1,2,JIA Dong1*,YIN Hongwei1,WEI Dongtao2,4,CHEN Zhuxin3,SUN Chuang1,CUI Jian1
1.Institute of Energy Sciences,School of Earth Sciences and Engineering,Nanjing University,Nanjing 210023,China 2.Key Laboratory of Reservoir Characterization,China National Petroleum Corporation (CNPC),Lanzhou 730020,China 3.Research Institute of Petroleum Exploration and Development,Petrochina,Beijing 100083,China 4.Research Institute of Petroleum Exploration and Development-Northwest (NWGI),Petro Lanzhou 730020,China
Abstract:The development of structural fractures and finite strain state are closely related in the oil and gas reservoir.In order to explore a new method of finite strain analysis and structural fracture prediction,this study designed and performed a set of sandbox experiments.The particle image velocimetry (PIV) technique was applied to quantitatively analyze the experimental process.The experimental model was a unilateral indentation model with a viscous layer in the vertical direction,and the results represent abook=172,ebook=175macroscopic box fold.Using the PIV technique,we can obtain the displacement field data during the deformation process in each stage of the experiments,calculate the incremental strain in each step,and analyze the finite strain state during the whole deformation process from the initial stage to the time after the fold was formed.Furthermore,the genesis mechanism and distribution can be discussed to quantiatively predict the fractures.At the beginning of the deformation,the finite strain was weak (about 4-8%) and widely distributed.Weak compressive linear strain was represented in the direction of indentation and weak tensile linear strain in the vertical direction.These phenomena were interpreted as the results of the pure shear deformation,such as the thickening and parallel shortening of the layers before the folding and faulting initiated.It is also the main mechanism of the formation of the regional tension fissures and shear cracks.The finite strain was localized in the fault zone and the adjacent area when the fold and fault formed.Strong shear and tensile shear strain (up to 20%) was revealed.These were the results of the simple shear deformation along the fault plane.It is also the main mechanism of the formation of the local shear fractures and tensile shear cracks.
Key words:analogue modeling; particle image velocimetry (PIV); finite strain analysis; tectonic fracture prediction
Corresponding author:JIA Dong,Professor; E-mail: djia@nju.edu.cn
*通讯作者:贾东,男,1960年生,教授,博士生导师,主要从事含油气盆地构造和活动构造研究;E-mail: djia@nju.edu.cn
作者简介:沈礼,男,1986年生,博士研究生,构造地质学专业;E-mail: nju.shenli2010@gmail.com
基金项目:江苏省科技项目(BE2013115);国家科技重大专项(2011ZX05009-001;2011ZX05003-002)联合资助
收稿日期:2015-11-30;修回日期:2016-03-07
DOI:10.16108/j.issn1006-7493.2015238
中图分类号:P618.13
文献标识码:A
文章编号:1006-7493(2016)01-0171-12

